Re＝3 900圆柱绕流的三维大涡模拟

战庆亮，周志勇，葛耀君

（土木工程防灾国家重点实验室（同济大学），200092上海）

Re＝3 900圆柱绕流的三维大涡模拟

战庆亮，周志勇，葛耀君

（土木工程防灾国家重点实验室（同济大学），200092上海）

为研究亚临界雷诺数范围内圆柱绕流流场特性及三维大涡模拟方法的适用性，基于C＋＋语言及有限体积法开发了三维非结构化网格的大涡模拟计算程序.采用新的高稳定性高精度二阶离散格式，及Smagorinsky亚格子模型对Re＝3 900均匀来流条件下的圆柱绕流问题进行数值模拟，并统计获得了平均流场参数及湍流流场的详细结构特性.结果表明：采用本文的网格、计算步长和高稳定性二阶离散精度大涡模拟方法计算所得的湍流场一阶统计特性和二阶统计特性与实验值吻合很好.验证了大涡模拟程序在模拟亚临界雷诺数下圆柱绕流流场平均值及脉动值的合理性.

Smagorinsky亚格子模型；圆柱绕流；亚临界雷诺数；非结构化网格；二阶延迟修正

圆柱绕流由于其几何形状简单，一直是钝体空气动力学、水动力学和风工程领域中的热点研究问题，对工程实际应用有着重大意义.圆柱绕流的流场特性取决于雷诺数（Re＝ρUD／μ，其中U为来流速度，D为圆柱直径，μ为运动粘性系数），绕流随流动Re数的变化呈现极复杂的变化特征.而处于亚临界情况下的圆柱绕流，有着丰富的流场特性和复杂尾流结构.

Re＝3 900情况下圆柱引起的湍流绕流问题是典型的亚临界雷诺数问题，随着计算机资源的发展，Re＝3 900圆柱绕流成为亚临界计算的一个典型算例［1］.Re＝3 900的亚临界圆柱绕流实验研究数据比较丰富，可以作为验证程序计算钝体亚临界雷诺数绕流准确性和算法适用性的标准，包括积分量（力，回流区长度等）和局部量（速度、涡量和雷诺应力等）.文献［2］使用热线风速仪（hot-wire anemometry，简称HWA）开创性的精确测量了回流区以外尾流的速度和涡矢量场，得到了湍流的统计信息和顺流及横向多处流场能谱.为了弥补HWA在流场回流区内部测量的不足，有学者采用激光粒子成像技术（简称PIV）和激光多普勒仪（LDV）来进行实验测量，如文献［1，3］采用PIV进行了近尾流区域内的流场结构更加细致和详细的测量.直接数值模拟（DNS）结果也用来作为一种标准，主要用来研究剪切层的失稳现象［4］.数值模拟方面，文献［5］首次对Re＝3 900的圆柱绕流进行了三维大涡模拟数值计算，采用的是O型贴体网格，近壁处的网格密度达到网格无关要求，平均速度和雷诺应力结果与实验结果吻合较好，但是在回流区内部流向速度差别较大；文献［6］基于B-splines高阶格式同样进行了计算，在回流区内部及外部都与实验较好的吻合，同时文中还指出展向网格数量不足将使剪切层提前脱落，导致不准确的结果；文献［7］基于C型曲面网格采用二阶守恒形式的中心差分大涡模拟格式，进行了同样雷诺数的计算，不同的是展向采用了谱方法离散，文中结果与实验值吻合较好，但是下游区的雷诺应力由于离散格式的数值粘性衰减较快.另外，文献［8－9］同样采用大涡模拟进行了Re＝3 900圆柱绕流模拟.文献［10］采用二维离散涡方法研究高雷诺数圆柱绕流问题，得到了较好的气动力结果；国内其他作者大多采用商业计算流体软件模拟圆柱绕流流场，如文献［11］采用Fluent软件进行了三维大涡模拟计算；文献［12］对高Re数圆柱绕流应用Fluent软件进行了二维的RANS分析，来讨论其适用性问题.

本文以直径D＝1.0 m的圆柱为研究对象，通过采用面向对象C＋＋语言编写的非结构化网格有限体积计算程序结合大涡模拟方法，采用精度高稳定性好的二阶离散格式，对Re＝3 900的圆柱绕流流场进行模拟.通过对计算得到的流场平均量与相关文献研究结果对比，评价本文程序的有效性和算法稳定性，为高Re数及复杂断面气动力特性数值研究提供建议.

1 模拟方法

1.1 流场控制方程及有限体积离散

本文计算采用非结构化网格下的离散程序，非结构化网格具有复杂区域适应性好、局部加密灵活和便于自适应的优点，在流体数值模拟中得到越来越广泛的应用.但在结构化网格中比较成熟的高阶格式很难直接用于非结构化网格中，因此提高精度和简化算法仍然是计算流体动力学研究的主要方向之一.对广义输运方程在控制单元体上进行积分，利用高斯定理将体积分转为面积分后得到［13］

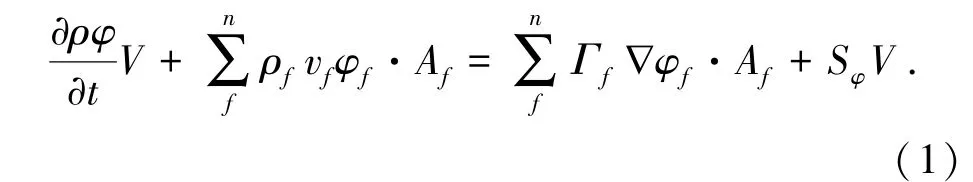
式中：φ为待求的标量，f表示单元体的面，n为围成单元体面的个数.在上述方程中，非结构化网格离散计算中的关键是提高对流项和扩散项的计算精度.上游格式的数值稳定性好，但是数值粘性较大，只有一阶精度.文献［14］提出将QUICK格式用于非结构化网格的构思，但是没有具体实现及研究.文献［15］推导了三角形控制体非结构化网格QUICK计算方法，但其对网格适用性有限且程序实现复杂，且难于应用到三维计算中.本文提出了一种适用于三维非结构网格中二阶精度格式，且数据结构简单.

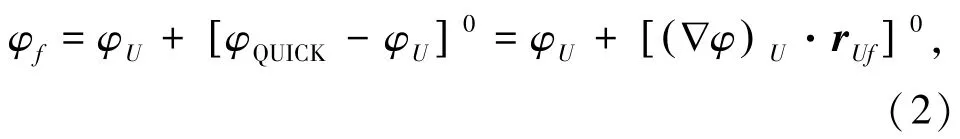
式中下标U表示上游单元体，rUf表示上游单元体中心指向面中心的矢量.例如图1中非结构化网格局部所示，f为面中心，C和N为单元体中心.若f面的外法向朝向单元N，则公式变为

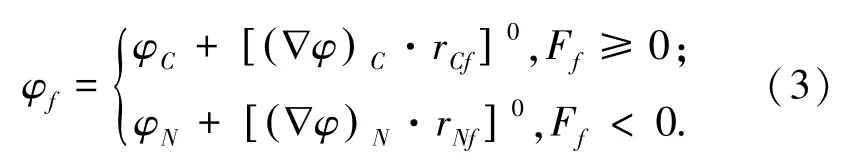
式中Ff＝Afρfφf（u·n）f为对流通量，n为面的外法向量.本格式的精度关键在于梯度的计算，可以采用高斯方法和最小二乘法，这两种格式都用到了单元体其余面的信息，包含了远场（即上游）的高阶影响，故可提高精度.梯度的计算要保证其有界性，本文采用了限制子方法（Limiter）.公式中上标0代表延迟修正项，也就是采用了显示处理，这样能提高计算稳定性同时不损失精度.由于速度与压力梯度的联系体现在动量方程中，而连续性方程中不显含压力梯度，本文采用Rhie-Chow动量插值技术［16］克服由非交错网格可能引起的非物理震荡问题.在时间上采用三层全隐式格式，具有二阶精度及良好的稳定性.

图1 非结构化有限单元体离散示意

1.3 网格划分与参数选择

本文计算域为：流向长度30D，横向长度20D，展向长度3D，其中D为圆柱直径.在圆柱周围5D范围内采用O型网格，网格数为205×185.展向方向的网格数30.在远离圆柱的流场区域使用较稀疏的网格，而近尾流区采用较密的网格，圆柱表面及局部网格见图2.靠近圆柱表面的第一层网格的厚度取为d＝0.003D，底层网格Y＋值约为1，保证大涡模拟的计算准确性，平面内单层网格数为44 000.为保证数值模拟的准确性，根据克朗数（Crount number）要求选取时间步长为0.05 s.

图2 圆柱表面及局部网格三维视图

2 三维LES数值计算结果与分析

图3显示了瞬时的分离剪切层和尾流涡脱的发展情况：圆柱两侧发展出两个剪切层，并在圆柱尾部交替断裂脱落，形成有一定周期规律的涡脱，在漩涡脱落区内部流场较为复杂.图中所示为低涡量等值面，其在离开圆柱一定距离之后发生失稳破碎，且具有明显的三维结构特征和无序性，随着流向方向逐渐减弱.在低涡量等值面中包裹着高涡量等值面，其结构尺度则更小，破碎效应更加明显.

图3 绕流流场瞬时涡量图

2.1 平均积分特性及一阶统计特性

平均积分特性和一阶统计针对平均流场参数进行，主要分别对固壁受到流体作用力、流场顺流方向速度、横向速度进行统计均值分析，是研究绕流流场特性的重要内容.表1对比了平均积分量（平均阻力系数Cd，斯特劳哈尔数Sr，平均回流长度r，最小平均速度Umin等量），与文献结果的差异很小.

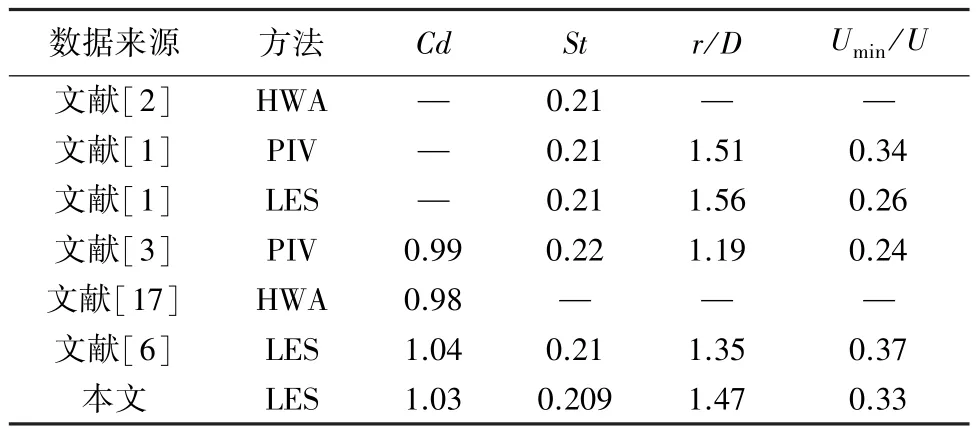
表1 积分特性对比

图4为漩涡稳定脱落后的阻力与升力系数时程曲线.阻力基本稳定在一定数值上，本文得到的平均阻力系数为1.03，这与实验和数值模拟结果都很接近.观察图4中升力系数时程，可以发现其均值为零，对比低雷诺数下圆柱绕流计算结果可发现，在亚临界雷诺数区间的升力系数幅值已不再平稳，随时间在一定范围内变化，然而仍存在明显的周期特性.

图5给出了中心平面（y＝0）上平均流向速度＜u＞分布情况.圆柱壁面处＜u＞为零，在流向方向由于存在回流区，因此＜u＞的值逐渐减小到Umin＝0.33.回流区中心的位置距圆柱中心位置也称为回流长度（recirculation length），用r表示.下游区＜u＞值逐渐变大，单调的逼近远处流场速度.图5显示本文计算结果与参考文献中的实验结果趋势及数值上吻合较好，尤其是与文献［1］近年的PIV实验吻合最好，该实验结果采用更为先进、精细的实验方法所得，因此认为其参数较以前文献中数据更为可信.

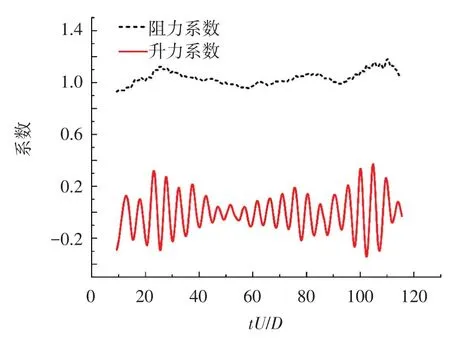
图4 阻力系数与升力系数时程曲线

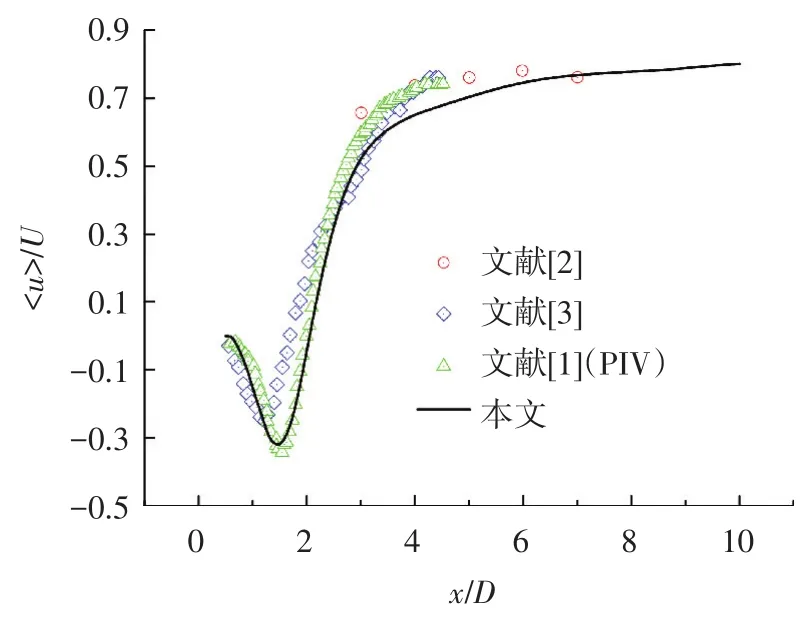
图5 中心平面处平均流向速度分布

图6为平均流场顺流速度云图，可以更加细致直观地分析尾流区流场结构，图7为平均横向速度云图.由图6可见，平均流向速度关于y＝0对称，这是由于本文研究的圆柱断面形状是对称的所致.在圆柱尾部有一个明显的＜u＞小于0的回流区，表明此处流场平均速度与顺流方向相反，这也是“回流区”名字的由来.文献［1，3］实验研究中，给出了尾流回流区域内及回流区域外不同位置处流向速度剖面图，因此本文也选取相应位置与实验值进行比对分析.在回流区内部，本文选取3个典型剖面进行分析，分别是x／D＝1.06，x／D＝1.54，x／D＝2.02；在回流区外部，本文也选取了3处典型位置，分别是x／D＝4.0，x／D＝7.0，x／D＝10.0来进行对比验证.

图8为尾流区6个位置处平均流向速度计算值与实验值的对比，其中黑色直线为本文结果，方形为文献［3］结果，三角为文献［1］中PIV实验结果，圆圈为文献［2］中实验结果（下文亦同）.本文计算结果与实验结果相比得到了很好的模拟效果.在回流区内部平均流向速度减速明显，很显然是由于钝体对流场的阻碍作用引起.同时还可发现平均流向速度剖面随着流场的发展由“U”字形逐渐变为“V”字形，其减速效应越来越区域平缓.在回流区内部，本文数值模拟结果与文献［1］的PIV实验结果更为接近.在回流区外部，平均顺流速度剖面更为平滑，且数值差异不大，表明在远离圆柱5D范围以外流场受圆柱影响已经较小.图9为相应尾流不同区域处平均横向速度剖面对比图，在回流区内部，图形形状为反对称，本文结果与文献［1］实验结果吻合较好，但与文献［3］试验值有一定误差.

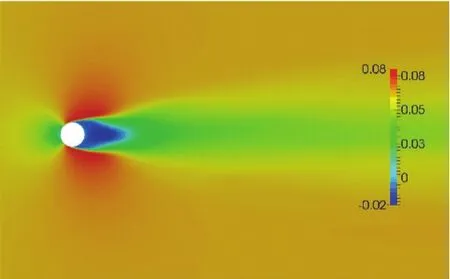
图6 平均流向速度云图

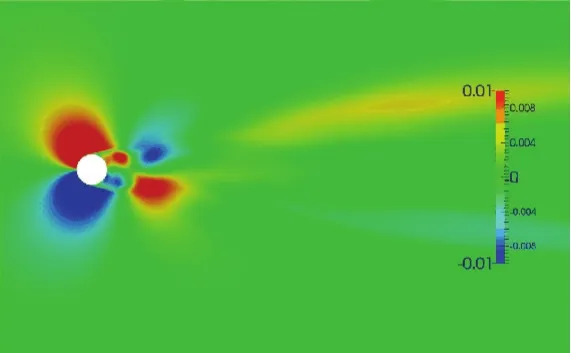
图7 平均横向速度云图

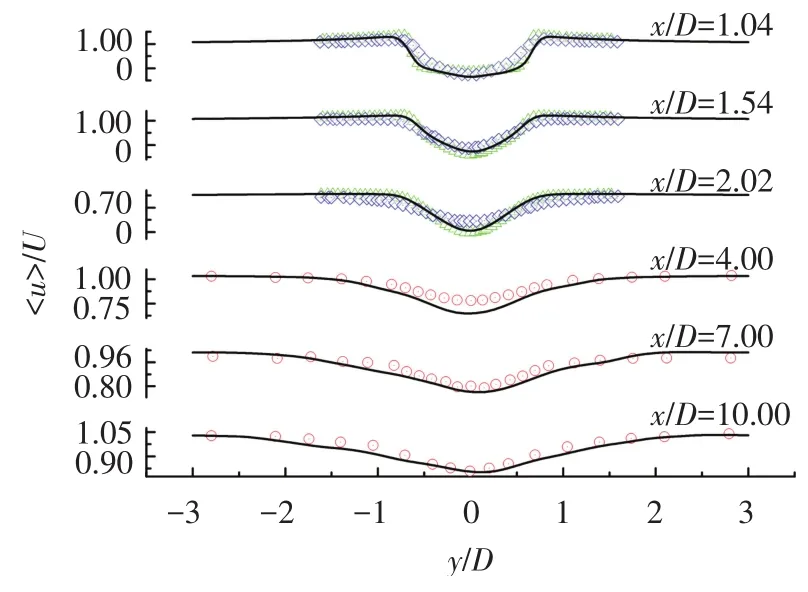
图8 尾流区不同位置平均流向速度分布

2.2 二阶统计特性

二阶统计特性主要对流场物理量的脉动值进行统计分析，代表了湍流流场的脉动特性，即雷诺应力的统计情况.对于湍流流动，速度的脉动情况、雷诺应力分布是湍流流动的重要特征.图10所示为中心平面处顺流向流场雷诺正应力的分布图.可以看出流向速度脉动沿顺流向的分布情况，在圆柱表面处其值为零，随着远离圆柱其值逐渐增大并达到两个峰，然后递减.本文与实验值及参考文件中数值模拟结果都显示远离圆柱的峰值较大，峰值处流场湍流雷诺应力较大.

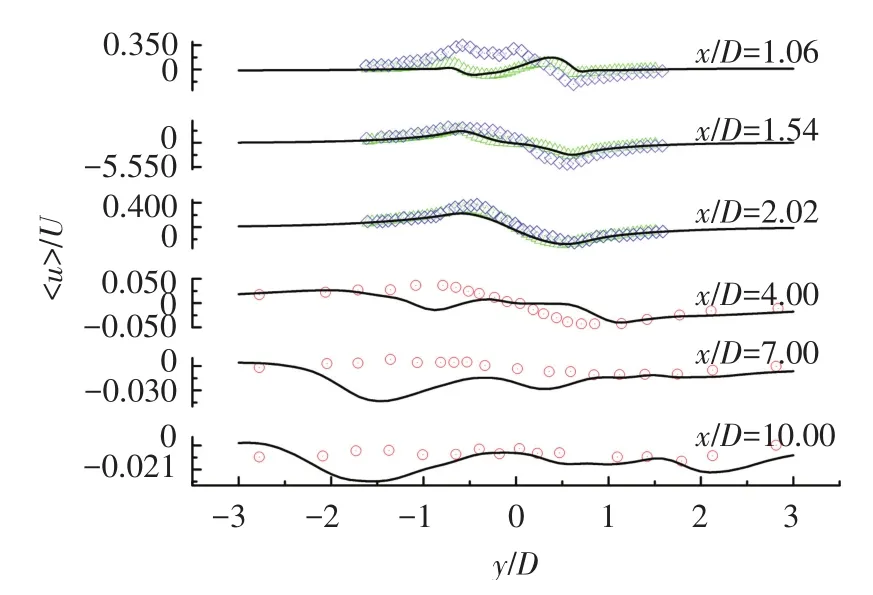
图9 尾流区不同位置平均横向速度分布

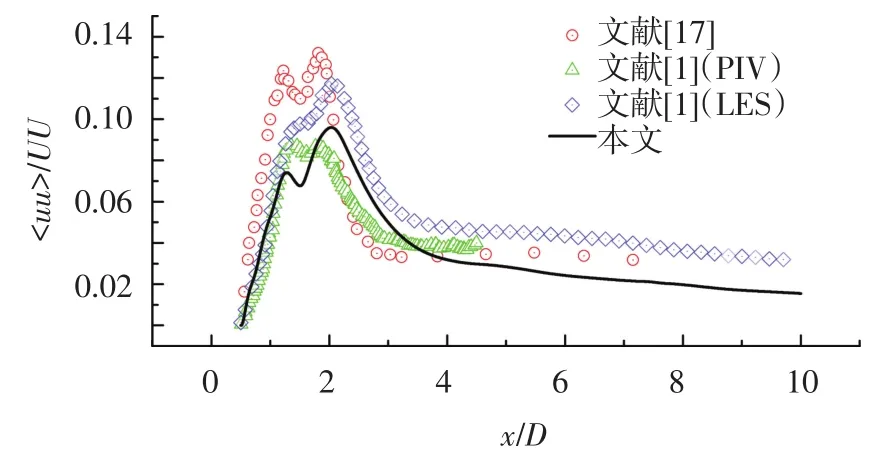
图10 中心平面雷诺应力分布

图11为顺流向速度脉动值平均云图.顺流向速度脉动值出现两处最大值，通过图10得该距离为2.044 7D.流向速度脉动值与漩涡脱落关系密切，最大值位置可以代表平均漩涡脱落的位置，同时两个峰值对应着圆柱两侧分别产生的漩涡.从流向速度脉动云图上可以得出：漩涡被拉长之后脱落，这种脱落形态与层流下的卡门漩涡脱落形态是不一样的.对比图13流场不同位置顺流速度脉动剖面图，可以发现本文结构很好吻合了实验结果.在x／D＝1.06处顺流向速度脉动均值出现两个尖角，这与实验中观察到的现象一致.本文认为这是由于圆柱两侧漩涡被流场拉伸至下游，而此处漩涡并未断裂，宽度也没有很大变化，反映在流向速度脉动剖面图上即为两个尖角形状.沿流线方向两侧漩涡半径变宽，同时发生断裂脱落现象，对应着x／D＝1.54，x／D＝2.02处的剖面曲线变得光滑，其值也变大.在尾流回流区外部处，可以看出顺流向雷诺应力平缓变小，此处的流场受圆柱绕流影响已经很小.

图11 流向速度脉动云图

图12为横向速度脉动云图，可以看出横向速度脉动最大峰值只有一个，这与顺流向速度脉动是不同的.图中表明横向脉动在中心线y＝0轴线上达到最大值，说明中心线处横向速度脉动量，即横向湍流应力最大，此处流场横向能量交换最为明显.图14中尾流区不同位置横向速度脉动分布图中观察到，在x／D＝1.06处横向速度脉动量非常小，说明在非常近圆柱处几乎没有横向脉动.其余各位置剖面图也与实验结果有很好的吻合度.

图12 横向速度脉动云图

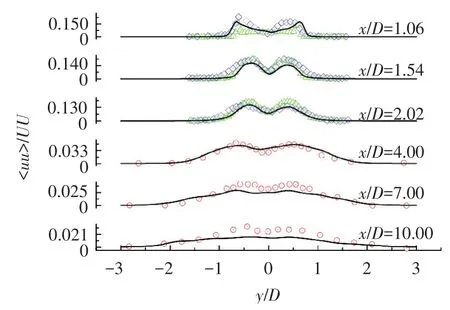
图13 尾流区不同位置流向速度脉动分布

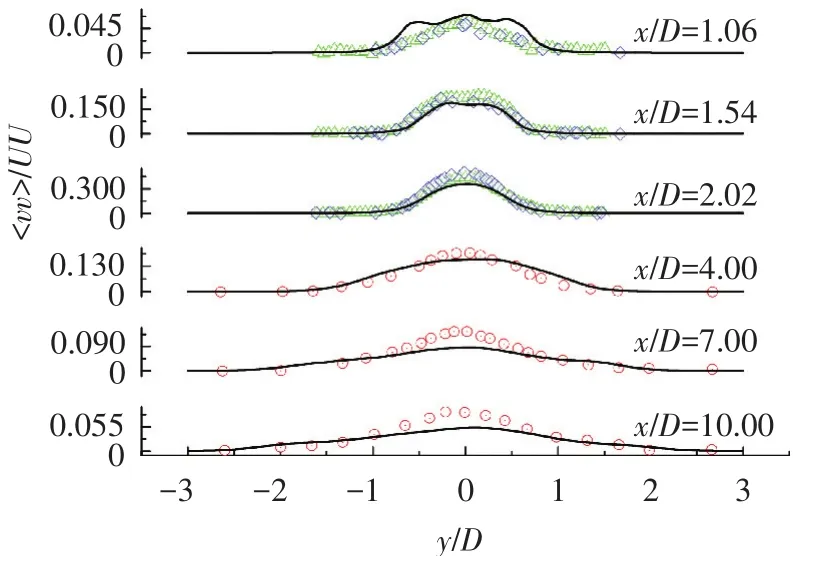
图14 尾流区不同位置横向速度脉动分布

3 结 论

1）针对一阶差分数值耗散过大和二阶中心差分数值稳定性差的问题，本文采用新的高稳定性二阶插值格式用于NS方程离散，并将其与延迟修正技术相结合，实现了较高精度、高稳定性的大涡模拟计算.

2）使用大涡模拟方法对亚临界雷诺数圆柱绕流流场进行计算模拟，对平均阻力系数、斯特劳哈尔数、回流区长度等平均积分量进行比较分析，验证其与实验值基本一致.

3）对流场尾流中心线及回流区内部和尾流区不同位置流场一阶统计特性和二阶统计特性进行统计，通过与相对应实验值进行对比，验证了本文计算的回流区内部和回流区外部尾流流场的平均值及脉动值的合理性.

4）通过对比验证，说明三维Smagorinsky亚格子模型以及本文离散格式可以准确模拟亚临界雷诺数圆柱绕流问题，并考证了本文采用有限体积法所开发程序的有效性.

［1］PARNAUDEAU P，CARLIER J， HEITZ D， et al.Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3 900［J］.Physics of Fluids（1994-present），2008，20（8）：85－101.

［2］ONG L，WALLACE J.The velocity field of the turbulent very near wake of a circular cylinder［J］.Experiments in Fluids，1996，20（6）：441－453.

［3］LOURENCO L M，SHIH C.Characteristics of the plane turbulent near wake of a circular cylinder：A particle image velocimetry study［Z］.Private Communication（data taken from［8］），1993.

［4］DONG S，KARNIADAKIS G，EKMEKCI A，et al.A combined direct numerical simulation-particle image velocimetry study of the turbulentnearwake［J］.Journal of Fluid Mechanics，2006，569（1）：185－207.

［5］BEAUDAN P，MOIN P.Numerical experiments on the flow past a circular cylinder at sub－critical Reynolds number［R］.Stanford：Stanford University，1994.

［6］KRAVCHENKO A G，MOIN P.Numerical studies of flow over a circular cylinder at ReD＝3 900［J］.Physics of Fluids，2000，12（2）：403－417.

［7］MITTAL R，MOIN P.Suitability of upwind-biased finite difference schemes for large-eddy simulation of turbulent flows［J］.AIAA Journal，1997，35（8）：1415－1417.

［8］FRANKE J，FRANKW.Large eddy simulation of the flow past a circular cylinder at＜i＞Re＜／i＞＜sub＞D＜／sub＞＝3 900［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（10）：1191－1206.

［9］LYSENKO D A，ERTESV G IS，RIAN K E.Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3 900 using the Open FOAM toolbox［J］.Flow，Turbulence and Combustion，2012，89（4）：491－518.

［10］周志勇.离散涡方法用于桥梁截面气动弹性问题的数值计算［D］.上海：同济大学，2001.

［11］周强，曹曙阳，周志勇.亚临界雷诺数下圆柱体尾流结构的数值模拟 ［J］.同济大学学报（自然科学版），2013，41（1）：33－38.

［12］祝志文.高Re数圆柱绕流二维数值模拟的适用性分析［J］.振动与冲击，2013，32（7）：98－101.

［13］FERZIGER J H，PERIC′M.Computational methods for fluid dynamics［M］.Berlin：Springer，2002.

［14］DAVIDSON L.A pressure correction method for unstructured mesheswith arbitrary control volumes［J］.International Journal for Numerical Methods in Fluids，1996，22（4）：265－281.

［15］姜华，席光.对流项二次迎风插值格式在非结构化网格中的应用［J］.西安交通大学学报，2006，11（1）：1246－1249.

［16］ISSA R I.Solution of the implicitly discretised fluid flow equations by operator-splitting［J］.Journalof Computational Physics，1986，62（1）：40－65.

［17］NORBERG C.An experimental investigation of the flow around a circular cylinder：influence of aspect ratio［J］.Journal of Fluid Mechanics，1994，258：287－316.

（编辑赵丽莹）

3-Dimensional large eddy simulation of circular cylinder at Re＝3 900

ZHAN Qingliang，ZHOU Zhiyong，GE Yaojun

（State Key Laboratory for Disaster Reduction in Civil Engineering（Tongji University），20092 Shanghai，China）

This paper developed finite volume method program with Smagorinsky sub-grid scale model using 3-dimensional unstructuredmesh to accurately determine the flow field characteristics behind a cylinder in sub critical region and the applicability of 3-dimensional large eddy simulationmethod of this kind of calculation based on C＋＋programming language.Numerical simulation was performed for the flow over a circular cylinder at a classical subcritical Reynolds number（Re＝3 900）using a new second order defer correction scheme for unstructured mesh.The results show thatmean and fluctuating flow characteristicswere compared wellwith the existing experimental results，2-order discretization scheme large eddymethod can be used in the simulation of sub-region Reynolds number outer flow simulation.The results also proved the reliability of high accuracy and stability discretization scheme.

Smagorinsky sub grid scale model；flow over a circular cylinder；sub-critical region；unstructured mesh；second order defer correction

U441

A

0367－6234（2015）12－0075－05

10.11918／j.issn.0367-6234.2015.12.013

2015－03－30.

国家自然科学基金重大研究计划集成项目（91215302）；国家重点基础研究发展计划（973计划）（2013CB036300）.

战庆亮（1987—），男，博士研究生；周志勇（1971—），男，研究员，博士生导师；葛耀君（1958—），男，教授，博士生导师.

周志勇，z.zhou＠tongji.edu.cn.