一种球面坐标下点面位置关系检测算法

刘文峰，徐雪仁，巫震宇，段卫国，赵锋锐

(北京遥感信息研究所，北京 100192)

一种球面坐标下点面位置关系检测算法

刘文峰，徐雪仁，巫震宇，段卫国，赵锋锐

(北京遥感信息研究所，北京 100192)

摘要点与多边形的位置关系是计算几何学领域的一个重要问题。在航空航天、地理遥感等领域需要高效精确的球面坐标系下的点与多边形位置关系检测算法，传统的平面逼近方法容易引入较大的误差。将平面内的射线法发展到球面坐标系下，采用3级级联处理的方法实现精确的位置关系检测。实验表明，本算法的正确检测率优于传统的平面逼近算法。

关键词球面坐标；多边形；位置关系；坐标变换

A Position Relationship Detect Algorithm for Points and Polygons in Spherical Coordinate System

LIU Wen-feng,XU Xue-ren,WU Zhen-yu,DUAN Wei-guo,ZHAO Feng-rui

(BeijingInstituteofRemoteSensingInformation,Beijing100192,China)

AbstractThe position relationship between points and polygons is an important problem in the field of computational geometry.The effective and precise algorithm for detecting positions between points and polygons is widely used in the fields of aerospace and geographical remote sensing.Significant bias is easily introduced in traditional planar approximation algorithm.This paper proposes an algorithm which evolves the planar ray method to the spherical coordinate system,and adopts a three-level cascade process to achieve precise position detection.The experiment results show that this algorithm has the correct detection rate better than that of traditional planar approximation algorithm.

Key wordsspherical coordinate system;polygon;position relationship;coordinate transformation

0引言

点与多边形的位置关系是计算机图形学、计算几何学、地理信息系统、CAD/CAM自动化系统等研究领域的一个重要问题[1]。目前已经有大量的成熟算法，如环绕法、角度相加法及射线法等[2,3]。但这些算法讨论的范畴仅限于平面坐标系。而在航空航天、地理遥感等研究领域，经常需要在球面坐标系下进行精确的数据处理，因此需要研究在球面坐标系下的点与多边形位置关系检测算法。

传统的研究方法是将球面逼近为平面来进行研究，在处理大量的地理数据和遥感数据时，不仅耗时耗资源，而且容易引入较大的定位误差[4,5]。本文借鉴平面坐标系下的射线法，将其发展至球面坐标系下，并针对球面坐标下的坐标变换、求交问题、特殊情况处理进行详细设计，从而精确判断点与球面多边形的位置关系。

1算法原理

1.1　基本概念

在球面坐标系下，多边形是由一系列大圆弧组成的封闭图形。球面上的任何区域和形状都可以用球面多边形来进行逼近。通常而言，连接球面上2点P和Q有2条大圆弧，在研究中通常只考虑较短的那条圆弧[6,7]。

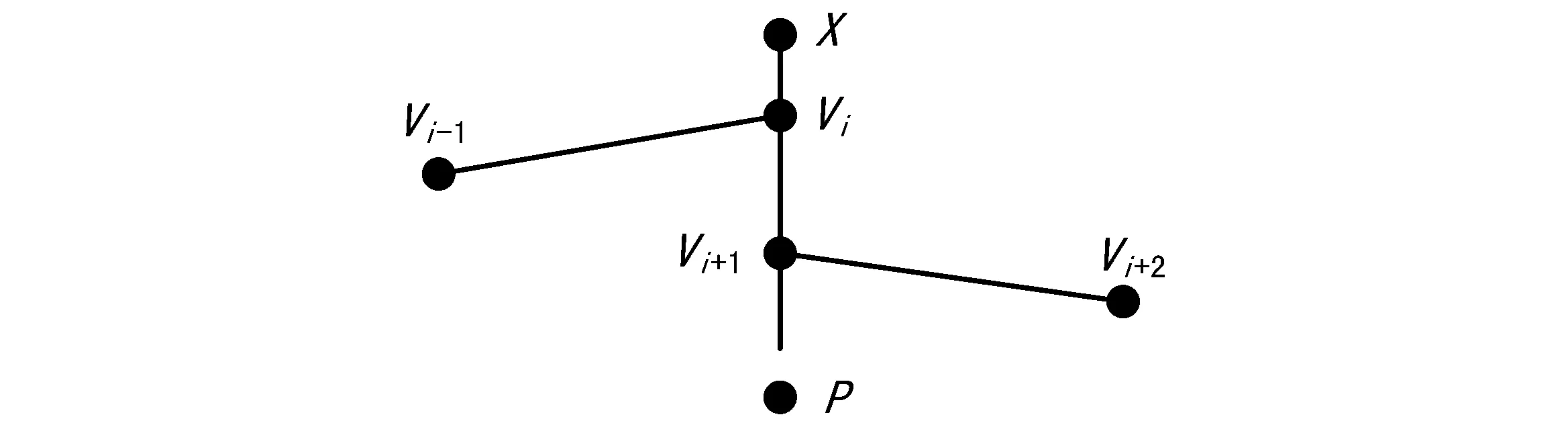
由n条边组成的球面多边形可以由其n个顶点完全确定，通常表示为R(V1,V2,…,Vn),每个顶点Vi的位置由其经纬度来确定，表示为Vi(λi,φi)。用于检测点与多边形位置关系的射线法原理可以描述为：已知一个球面多边形S和多边形之外的一个点X，对于任何一点P，如果连接X和P的大圆弧XP穿过多边形S的边界的次数为偶数的话，那么P在多边形外部。如果次数为奇数，那么P在多边形内部，如图1所示。因此，点与多边形位置关系的检测问题就转化为圆弧XP与多边形各边的求交问题。

图1　射线法原理

1.2　球面求交问题

为了判断圆弧XP和多边形的边AB是否相交，首先判断相交的必要条件，即以X为基点的圆弧XP的方位角是否位于圆弧XA和XB之间，如图2所示。必要条件的检测可以通过球面坐标变换来实现，将X点变换为新球面坐标系(λ′,φ′)的北极点，并使新坐标系的零经线通过原坐标系的北极点。那么圆弧XA,XB,XP的方位角就转化为新坐标系下点A,B,P的经度，由下式给出[8,9]：

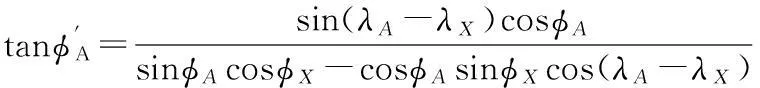
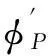
满足必要条件的点P不一定能保证XP和AB相交，如图中的点P2。因此还要进行进一步的充分性检测。为了保证圆弧XP和AB相交，那么X,P两点必须要位于圆弧AB两侧。同样的，可以用球面坐标变换来实现，如图3所示。在新的球面坐标系(λ″,φ″)中，点A为北极点。如果点X和P的经度值位于点B的经度值两侧，那么圆弧XP必然与圆弧AB相交。特别的，如果β=0，那么点P正好位于圆弧AB上。

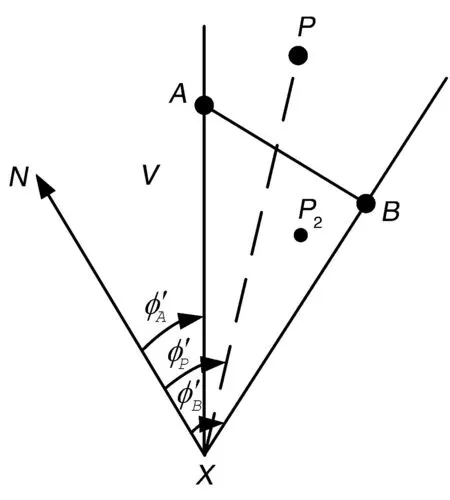
图2　必要性条件

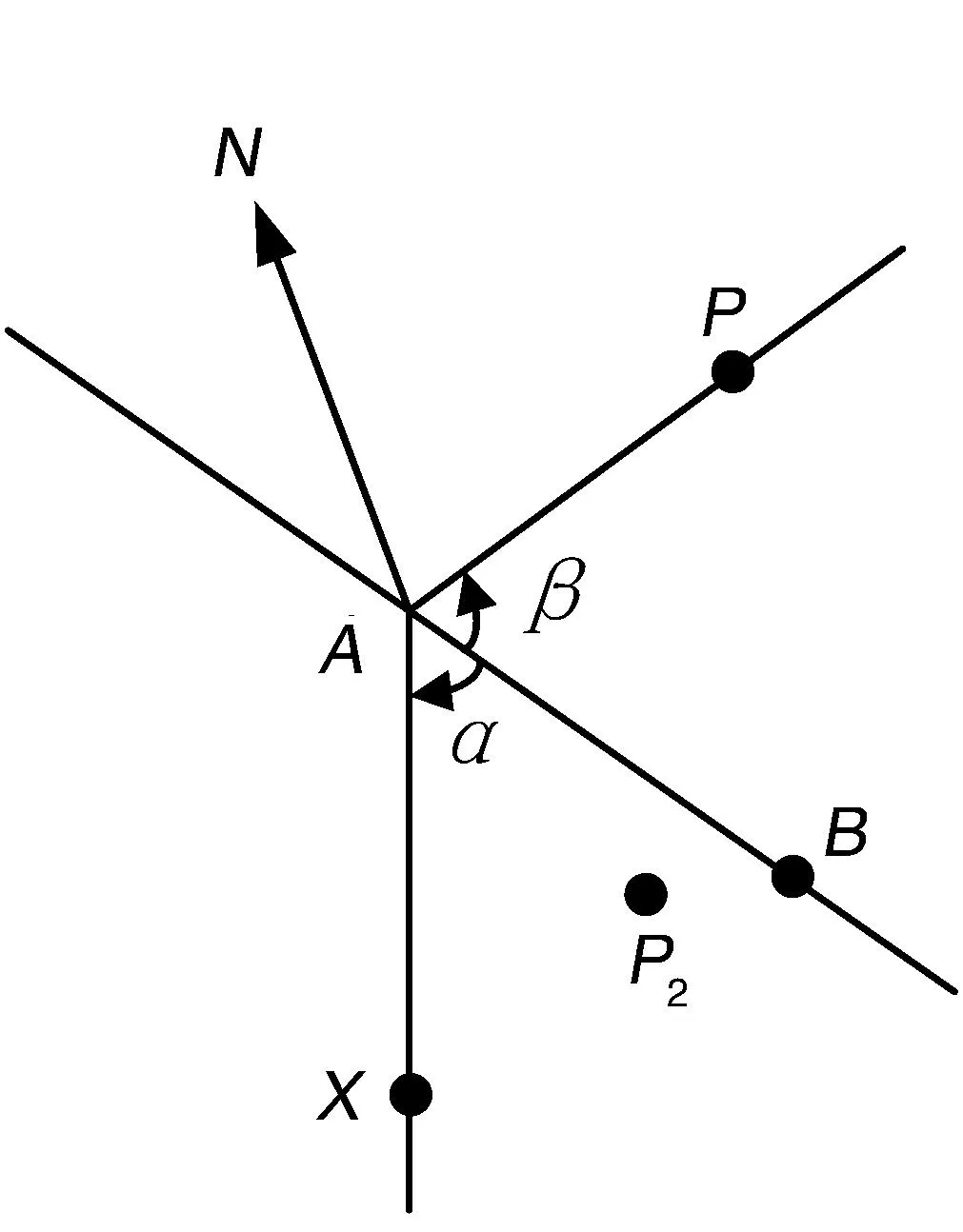
图3　充分性条件检测

1.3　特殊情况的处理

在检测算法的运行过程中，有几个特殊情况需要进行仔细处理以保证算法的顺利运行。首先是点X和点P正好为对极点，即连接点X和点P的直线为球面坐标系的直径。此时，连接XP的大圆弧不是唯一的，而有无数条，算法无法进行。对于这种情况，选择球面多边形S内部的另外一个点X2，重复进行上述判断即可完成位置关系的检测。

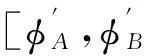
圆弧XP和圆弧AB同处于一个球面大圆上也是一种特殊情况，此时圆弧XP和圆弧AB是否相交很难定义。这种情况可以通过对点X的位置进行限定来避免，即在算法开始选择点X时禁止其处于多边形的任何一边的大圆上。此外，也可以通过对坐标系(λ′,φ′)中点A,B和P的纬度进行判断来排除。

1.4　算法的具体实现

当实际的应用中，算法的处理流程如下：

① 读取待处理的球面多边形R(V1,V2,…,Vn)和点P的坐标数据，选取另一端点X；

② 对于球面多边形R的每条边AB(ViVi+1)，进行圆弧XP和AB相交的必要性条件检测；

③ 对于通过必要性检测的圆弧AB，进行圆弧相交的充分性条件检测；

④ 进行特殊情况的处理，得到圆弧XP与球面多边形R各边的相交次数，从而判断点P与球面多边形的位置。

在实际应用中，通常可以选择北极点(或南极点)作为上述算法中的点X，这样可以减少算法的运算量。在运算前，首先以北极点P0作为点X，判断其是否在待处理的球面多边形区域中。如果不在，那么按照上述算法进行处理即可；如果在，将算法检测的结果取反。

判断北极点P0是否在球面多边形区域中时，可以将球面多边形和北极点都投影至赤道平面，判断投影区域是否包含北极点。如果不包含，那么北极点就不在球面多边形内部。如果包含，继续区球面多边形在北半球的子区域，进一步判断新区域的投影区域是否包含北极点。如果是，那么北极点就在原球面多边形区域中，算法最后的检测结果要取反。

对于上述的第3种特殊情况，如图4所示。如果按照左闭右开的边长区间[Vi,Vi+1)判断，圆弧XP与多边形各边的相交次数会增加2，而实际上只能按照增加1来处理，最终检测结果才不会出现误判。判断的方法如下：

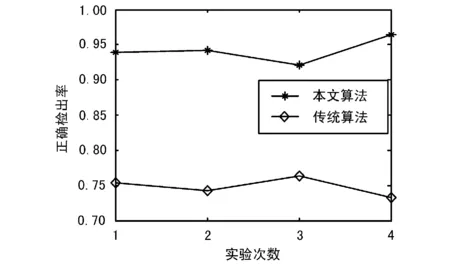
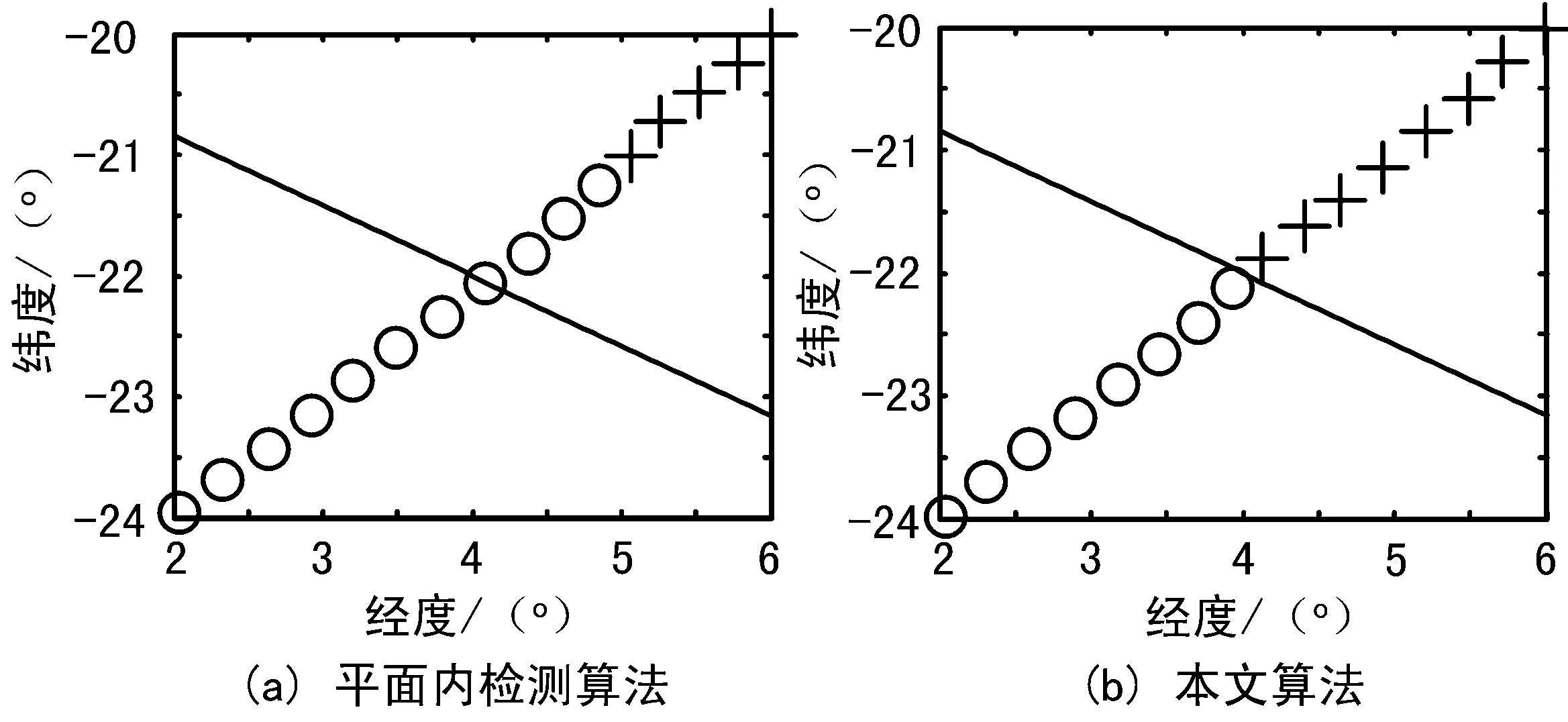
如果λP>max(λi,λi+1)，不计入相交次数;如果λP

图4　圆弧重合的特殊情况

2实验验证

为了验证本文算法的性能，随机生成100个点组成球面多边形。在其各边附近随机生成10 000个待检测点，利用本文的算法检测和球面多边形的位置关系。同时利用将球面近似为平面的检测方法进行对比试验。检测结果的正确性可以用立体几何检测法来验证。实验得到的检测性能如图5所示。其中，各点的位置经度精确到0.01°。

图5　算法性能对比

南大西洋辐射异常区(SAA)是指位于南美洲东边的南大西洋地磁异常区域，该区域高能带电粒子的辐射通量非常大，很多高能探测设备在经过该区域时需要关闭或者停止工作[7]。因此，精确检测卫星进出SAA区域的时机对于卫星有效载荷的正确运行具有重要意义。本文选取硬X射线调制望远镜(HXMT)为检测对象，利用传统的平面内算法和本文算法进行比较。当卫星的位置采用间隔为40 s时，2种算法的检测结果基本类似。而当采用间隔为1 s时，2种算法的检测性能差别很大，如图6所示。图中的实线表示SAA区域的边界，点为卫星轨迹，”o”表示区域内部，”+”表示区域外部。很明显，本文算法的检测结果非常精确。

图6　SAA区域检测

3结束语

将平面内点和多边形位置关系的射线检测算法发展到球面坐标系下。根据球面几何的相关理论对算法进行了发展，算法包括必要性条件检测、充分性条件检测和特殊情况处理3个主要环节，通过3个环节的顺序检测得到球面坐标系下点和多边形的位置关系结果。基于Matlab软件设计了验证实验，结果表明，本文算法对于大量边界点的检测能达到95%的正确检测率，远高于平面逼近算法。同时通过南大西洋辐射异常区的实验充分显示了本算法的优越性。本文的研究结果可以广泛应用于遥感、航空航天和计算机图形学等领域。

参考文献

[1]孙家广.计算机图形学[M].北京：清华大学出版社,1998.

[2]ASHOURIAN M，ENTESHARI R，JEON J.Digital Watermarking of Three-dimensional Polygonal Models in the Spherical Coordinate System [C]∥Computer Graphics International,2004:590-593.

[3]HORMANN K,AGATHOS A.The Point in Polygon Problem for Arbitrary Polygons[J].Computational Geometry:Theory and Applications-COMGEO,2001,20(3):131-144.

[4]OHBUCHI R，MASUDA H，AONO M.Watermarking Three-dimensional Polygonal Models Through Geometric and Topological Modifications[J].Selected Areas in Communications,IEEE Journal on,1998(5):909-969.

[5]SUNDARESWARA R， SCHRATER P.Extensible Point Location Algorithm[C]∥Geometric Modeling and Graphics,2003.Proceedings.2003 International Conference on,2003:85-89.

[6]郑顺义,邓德彦.基于三角网无缝拼接的三维重建[J].武汉大学学报(信息科学版),2009(1):32-36.

[7]黄跃,陈黎,卢宇.点在球面多边形内外的判定方法及应用[J].天文研究与技术,2011(4):31-33.

[8]顾祥龙,王元钦,郑海昕,等.基于MATLAB并行处理的前向定时同步方法研究[J].无线电通信技术,2013,39(3):36-38,42.

[9]SHINAGAWA Y，KAWAMICHI R， KUNII T L，et al.Developing Surfaces[C]∥Shape Modeling International,2002.Proceedings,2002:253-260.

[10]李源泉,申建平.多目标自动运行系统设计[J].无线电工程,2012,42(6):35-38.

[11]ZHANG Wen-li.Real-time Tree Model Reconstructing for Fruit Harvesting Robot System[J].2008 9th International Conference on Computer-Aided Industrial Design and Conceptual Design,2008(11):580-584.

[12]陈旸,赵祖松,黄巍.同时数字多波束技术实现雷达三坐标搜索[J].无线电工程,2013,43(9):45-47,64.

刘文峰男，(1986—)，工程师/博士。主要研究方向：卫星任务控制技术。

徐雪仁男，(1965—)，研究员，博士。主要研究方向：卫星任务控制技术。

作者简介

收稿日期：2015-05-12

中图分类号TP391.41

文献标识码A

文章编号1003-3106(2015)08-0047-04

doi:10.3969/j.issn.1003-3106.2015.08.13

引用格式：刘文峰，徐雪仁，巫震宇，等.一种球面坐标下点面位置关系检测算法[J].无线电工程，2015，45(8)：47-50.