基于翻转操作的(2, n)异或图像分存方案

欧锻灏， 吴小天， 程斌宜， 孙 伟,3

(1. 中山大学信息科学与技术学院，广东 广州 510006；2. 中山大学软件学院，广东 广州 510006；3. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093)

基于翻转操作的(2, n)异或图像分存方案

欧锻灏1， 吴小天1， 程斌宜2， 孙 伟2,3

(1. 中山大学信息科学与技术学院，广东 广州 510006；2. 中山大学软件学院，广东 广州 510006；3. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093)

通过翻转操作来构造图像分存方案的新方法。所构造的分存方案将秘密图像以一种无需任何密码学知识的安全方式进行编码，且无需额外地隐藏处理过程就能生成有意义的分存图像。该分存方案没有像素膨胀，且不需要设计码本。秘密黑色像素的重构是完美的，所有的秘密黑色像素都能够被精准地恢复。首先利用翻转操作构造一个有意义的(2, 2)方案，继而扩展出一个有意义的(2, n)方案。理论证明和实验结果表明了提出的分存方案正确和有效。

秘密图像分存；翻转操作；有意义的分存图像；完全性黑的；异或操作

Blakley[1]和 Shamir[2]于 1979年提出了将一个秘密分成几份的秘密分存方法。在该分存方法中，除非收集到足够多的分存份额，否则任何人都不可能得到秘密信息。视觉密码 (visual cryptography,VC)[3]是一种特殊的秘密分存，它将一幅秘密图像进行编码，生成几幅随机的图像。在(k, n)VC方案中，叠加k幅或者更多的随机分存图像可以显示出秘密图像的信息。但是，k–1或者更少随机图像将无法得到秘密图像的任何信息。VC不同于一般的图像加密方法[4-5]，它增加了秘密的冗余，降低了秘密图像丢失的风险性。由于视觉密码方案具有解码简单快速的优点，许多学者对其进行了广泛地研究[6-8]。不幸的是，由于叠加操作解密的缘故，产生的分存图像和重构图像在视觉效果上都不尽如人意。此外，在叠加解密过程中，还遭遇像素对齐的问题。这些问题导致视觉密码在应用上的局限性。

为了解决传统 VC中低视觉效果和像素对齐的问题，一种利用“异或”操作取代“叠加”操作来解密图像的分存方案[9-10]产生了。相比之下，基于“异或”操作的分存方案解决了像素膨胀，低视觉效果和像素对齐等问题。但是，目前大多数基于异或操作的分存方案所产生的分存图像是一个无意义的、随机图像。产生有意义的分存图像对分存图像的管理上具有很大的意义，所以大多数学者致力于研究有意义的图像分存方案[6,11-12]。

本文构造了一个能够产生有意义分存图像的、基于翻转操作的(2, n)异或图像分存方案，并可利用异或操作代替“叠加”操作对秘密图像进行解密。本文方案满足秘密分存概念中的安全性和对比度的条件，而且具有无码本和无像素膨胀的优点。除此之外，本文所提出的图像分存方案还具有如下优点：

(1) 可以直接产生有意义分存图像，且不需任何额外的隐藏处理过程。

(2) 获取更好视觉效果的恢复图像和分存图像，且解决了像素对齐的问题。

(3) 黑色像素的重构是完美的，这意味着所有秘密黑色像素能够被精准恢复。

(4) 大量的形式化证明验证了本文分存方案的正确性。

1 相关工作

VC是秘密分存概念在数字图像上的应用。VC将秘密图像以一种无需任何密码学知识的安全方式进行编码。在传统的视觉方案中，解密的基本操作是“或”操作。使用“或”操作进行解密虽然简单、快捷，但经常遇到视觉质量差、像素对齐、需要码本以及像素膨胀等问题。为了解决上述问题，另一种基于异或的图像分存方案产生了，它同样将秘密图像以一种安全方式进行编码。与VC方案不同的是，异或图像分存方案将使用“异或”操作来代替“叠加”操作对秘密图像进行解密。

定义1. 平均透光率：对于大小为H×W的二进制图像I中的一个像素p，p为白色的概率表示为Prob(p=1)，p的透光率记为T(p)。当p为白色像素时，p的透光率为T(p)=1；反之，当p为黑色像素时，p的透光率为T(p)=0。那么，图像I的平均透光率可以定义为：

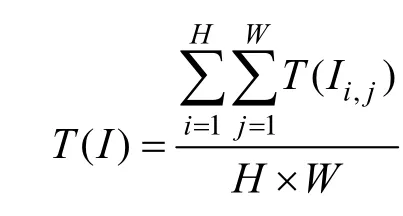
定义2. 区域表达：令A(1)(或A(0))表示图像A中的所有白色(黑色)区域，其中 A=A( 1) ∪A(0)且A( 1) ∩ A(0)=Ø。B[A(1)](或B[A(0)])表示A中所有白色(黑色)像素在图像B中的相应区域。

定义3. 恢复图像对比度：为了评估由R{⊕,1,··,n}= R1⊕···⊕ Rn所得恢复图像的视觉质量，相较于初始秘密图像S，恢复图像对比度定义为：

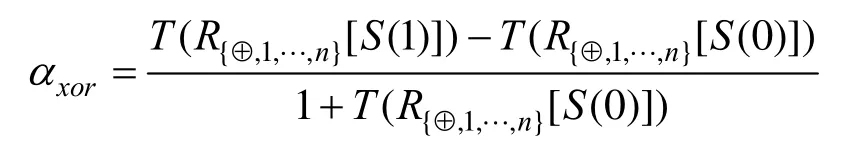
其中，R1,… ,Rn表示分存图，⊕表示异或运算。

定义4. (分存图像对比度)相对于初始载体图像C，分存图像R的对比度可定义为：

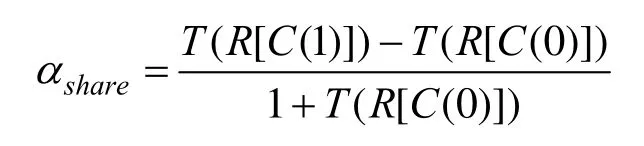
2 异或图像分存方案

本小节首先利用翻转操作构造一个有意义的(2, 2)异或图像分存方案；随后，将(2, 2)方案通过扩展得到一个有意义的(2, n)异或图像分存方案。同时，还可提供形式化证明来验证异或图像分存方案的有效性。

2.1 有意义的(2, 2)异或图像分存方案

算法1给出了基于翻转操作的(2, 2)异或图像分存方案的构造过程。

算法 1. 无意义的(2, 2)异或图像分存方案的构造。

输入：二进制图像S和载体图像C，S和C的大小均为H×W。

输出：两个大小为H×W的分存图像R1和R2。

步骤1. 对分存图像R1和R2进行初始化，得到：

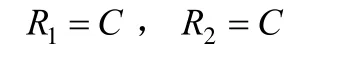
以下将根据秘密图像S的像素值，对这两幅初始化后的分存图像中的像素值执行翻转操作，具体描述如下。

步骤2. 对秘密图像上的每一位置(i, j)，根据 S( i, j)值的不同，将对初始像素 R1( i, j)和 R2( i, j)采取不同的翻转策略。

步骤3. 当 S( i, j)= 0时，以 1/2的概率对 R1( i, j)和R2( i, j)同时进行翻转。

步骤4. 当 S( i, j)= 1时，以相等的1/2概率从 R1( i, j)和R2( i, j)中随机选择一个，并进行翻转，而未选中的那个则保持不变。

步骤 5. 重复步骤 2~4直到所有秘密像素均被处理完毕，即可输出分存图像R1和R2。

注意：算法 1在无需码本和像素膨胀的情况下，通过翻转操作来实现异或图像分存方案。但是，由算法 1所生成的分存图像是一个随机的、无意义的图像。为了生成有意义的分存图像，可在算法1的基础上引入一个概率参数β，以此来构造一个有意义的(2, 2)异或图像分存方案，具体描述见算法2。

算法 2. 有意义的(2, 2)异或图像分存方案的构造。

输入：大小为H×W的秘密图像S，大小为H×W的载体图像C，和概率参数β(0 ＜ β＜1)。

输出：两个大小为H×W的有意义分存图像R1和R2。

步骤1. 对于秘密图像S上的每一位置(i, j)，将按照以下步骤来生成分存像素值 R1( i, j)和 R2( i, j)。

步骤2. 随机生成一个比特d，它为1的概率是β，为0的概率是1 - β。

步骤3. 当 d=1时，利用算法1生成两个分存像素值，即：

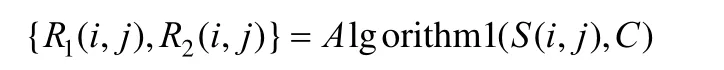
步骤4. 当 d= 0时，用 C( i, j)直接赋值给两个分存像素值，即：

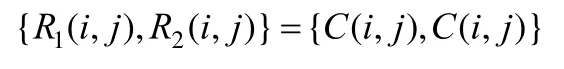
步骤 5. 重复步骤 1~4直到所有秘密像素均被处理完毕，即可输出有意义的分存图像R1和R2。

定理1. 设R1和R2为带参数β的算法2所生成的分存图像。算法2是一个有意义(2, 2)异或图像分存方案的有效构造方法，其应满足如下条件：

·安全性：每个分存图像都不能给出秘密图像的任何信息： T( Rk[ S (0)]) =T( Rk[ S (1)])，其中，k=1,2。

·有意义：每个分存图像都是一幅类似载体图像的有意义图像：T( Rk( C (1))) ＞T( Rk( C(0)))，其中，k=1,2。

·对比度：两个分存图像的异或结果R{⊕,1,2}= R1⊕ R2能恢复出秘密信息：

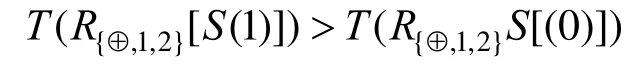
且异或结果不会得到载体图像的任何信息：

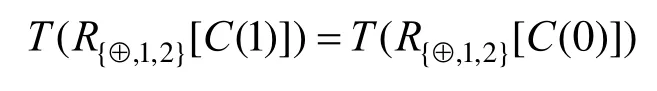
证明. 算法2中，针对每一秘密像素S(i, j)，以β的概率执行步骤3，以1–β的概率执行步骤4。执行步骤3时，无论秘密像素为1或0，分存像素R1( i, j)和 R2( i, j)均以1/2的概率进行翻转，因此，Pro b( Rk( i, j) =1|S( i, j) =0)= Pro b( Rk( i, j) =1|S( i, j)=1) (k = 1,2)。执行步骤 4时，分存像素 R1( i, j)和R2( i, j)的值与秘密像素的值无关。所以，可以得到 ：Pr ob( Rk( i, j) = 1|S( i, j) =0) = Pr ob( Rk( i, j )= 1|S( i, j)= 1)(k = 1,2)。由定义 1、2可知，T( Rk[ S (0)]) =T( Rk[ S(1)])(k = 1,2)。综上可得，任一分存图像均不会给出秘密图像的任何信息。

当载体图像像素 C( i, j)= 0(或 C( i, j) = 1)时，相应的分存像素 R1( i, j)和 R2( i, j)的平均透光率为由0 ＜ β＜1可知，因此，T( Rk(i, j)[C( i, j) =1]) ＞ T( Rk(i, j)[C( i, j ) =0]) (k = 1,2)， 又 由 定 义 1、2 得 出 ，T( Rk[ C (1)]) ＞T( Rk[ C(0)])。综上可得，每个分存图像都是类似于载体图像的有意义的图像。

以概率β执行步骤3时，若 S( i, j)= 1，则由两个分存像素所得的异或结果的平均透光率为1，反之，若S(i,j)=0，则相应的平均透光率为0。因此：

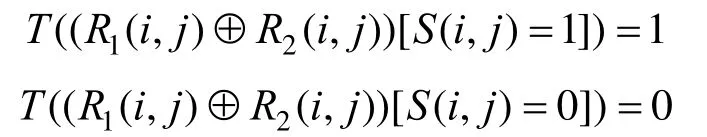
以概率1- β执行步骤 4时，由两个分存像素所得的异或结果的平均透光率为T ((R1(i, j) ⊕R2(i, j ))[S ( i, j) =1]) = T ((R1(i, j )⊕R2( i, j) )[S( i, j) = 0])，这是因为两个分存像素是相同的，且独立于秘密像素。基于上述分析，进行加权计算即可得到： T ((R1( i, j) ⊕R2( i, j) )[S( i, j) =1])＞T ((R1( i, j) ⊕ R2( i, j )) [S( i, j)= 0])。由定义1、2可知， T((R1⊕ R2)[S (1)]) ＞T((R1⊕ R2)[S(0)])。因此，两个分存图像的异或结果可以恢复出秘密图像信息。

由算法2的描述可知，针对每个秘密像素S(i,j)，每幅载体图像的像素C(i,j)均以β/2的概率进行翻转。所以得到：

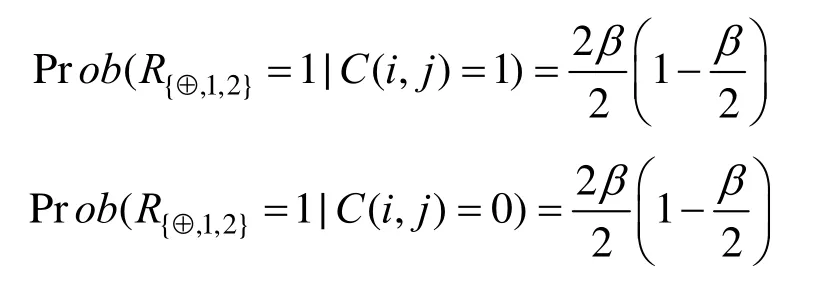
定理2. 设R1和R2为带概率参数β的算法2所生成的分存图像，则两个分存图像异或结果的对比度为：xorα β= 。

证明. 当两个分存像素由算法2的步骤3生成，若秘密像素为1，则相应异或结果的透光率为1，反之，若秘密像素为0，则相应透光率也为0。由定理 1的证明可得，如果两个分存像素是由算法2的步骤4所生成，则无论秘密像素为1还是0，其异或结果的透光率恒为0。又因为执行步骤3的概率为 β，执行步骤 4的概率为 1–β，可得如下两点：

(1) 异或结果相对应于秘密图像白色区域的平均透光率为：

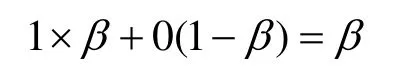
(2) 异或结果相对应于秘密图像黑色区域的平均透光率为：

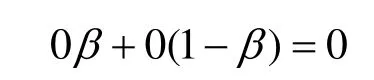
由定义3，两个分存像素异或结果的对比度计算如下：

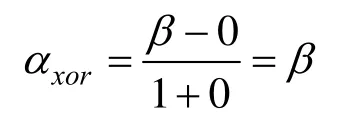
定理3. Rk(k=1,2)是由带概率参数β的算法2所生成的分存图像，其对比度为：

证明. 如果分存像素由算法2的步骤3所生成，当相应的载体图像像素为1(或0)时，其平均透光率为1/2(或1/2)。如果分存像素由算法2的步骤 4所生成，当相应载体图像像素为 1(或 0)时，其平均透光率为 1(或 0)。因为执行步骤 3的概率为β，执行步骤4的概率为1–β，可得如下两点：

(1) 分存图像相对应载体图像白色区域的平均透光率为：

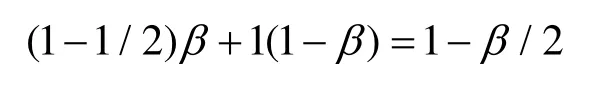
(2) 分存图像相对应载体图像黑色区域的平均透光率为：

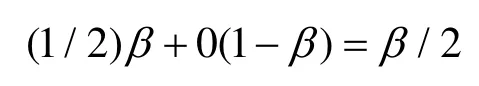
由定义4可得，分存像素Rk的对比度计算公式为：

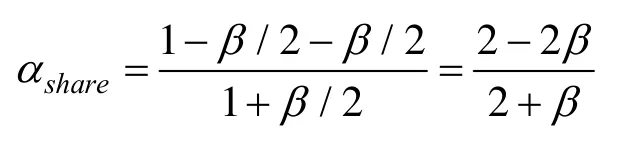
2.2 有意义的(2, n)异或图像分存方案

若将(2，2)方案扩展得到(2, n)异或图像分存方案。值得注意的是，扩展所得的(2, n)异或图像分存方案的解码过程与传统的(2, n)方案有些不同。在传统的(2, n)方案中，当分存图像数量 2k＞ 时，k个分存都将用于解码秘密图像。而在扩展所得的(2, n)方案中，只需要其中的任意两个分存图像来解码。

算法 3. 有意义的(2, n)异或图像分存方案的构造。

输入：大小均为H×W的秘密图像S和载体图像C，参数β(0 1)β≤ ≤ 。

输出：n个大小为H×W的有意义分存图像R1,…,Rn。

步骤1. 对于秘密图像S上的每一像素S(i,j)，将按照以下步骤生成相应的分存像素值。

步骤2. 生成一个比特d，它为1的概率是β，为0的概率是1–β。

步骤3. 当 1d=时，首先将n个分存像素初始化为载体图像像素C(i,j)，即：

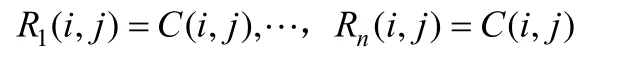
随后，对这n个像素进行翻转操作。当S(i,j)=0时，以1/n的等概率对n个分存像素同时进行翻转；当S(i,j)=1时，将以1/n的等概率随机选择其中一个分存像素进行翻转，而其余n-1个分存像素保持不变。

步骤4. 当 0d= 时，直接令n个分存像素值等于C(i,j):

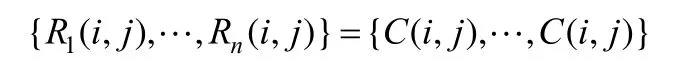
步骤 5. 重复步骤 1~4直到所有秘密像素全部处理完毕时，便可得到n个有意义的分存图像R1,…,Rn。

为了得到一个有意义的(2, n)异或图像分存方案，参数n和β应满足如下条件：

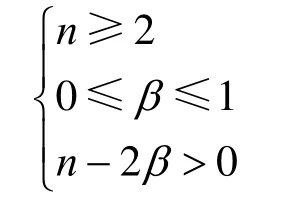
同样地，用类似证明算法 2的分析方法，可以证明算法3的正确性。并且可以得到算法3所产生的分存图像的对比度为：同时，可以得到任意两个分存图像异或结果的对比度为：

3 实验结果及讨论

3.1 可行性

本小节通过以下实验来验证异或分存方案的可行性。第一个实验是由算法2生成的(2，2)方案，其中参数β=0.5，图像大小为512×512，实验的结果见图1。由图观察可得，每一幅有意义的分存图像均不能给出秘密图像的任意信息。但是，两幅分存图像的异或结果可以恢复秘密图像信息。

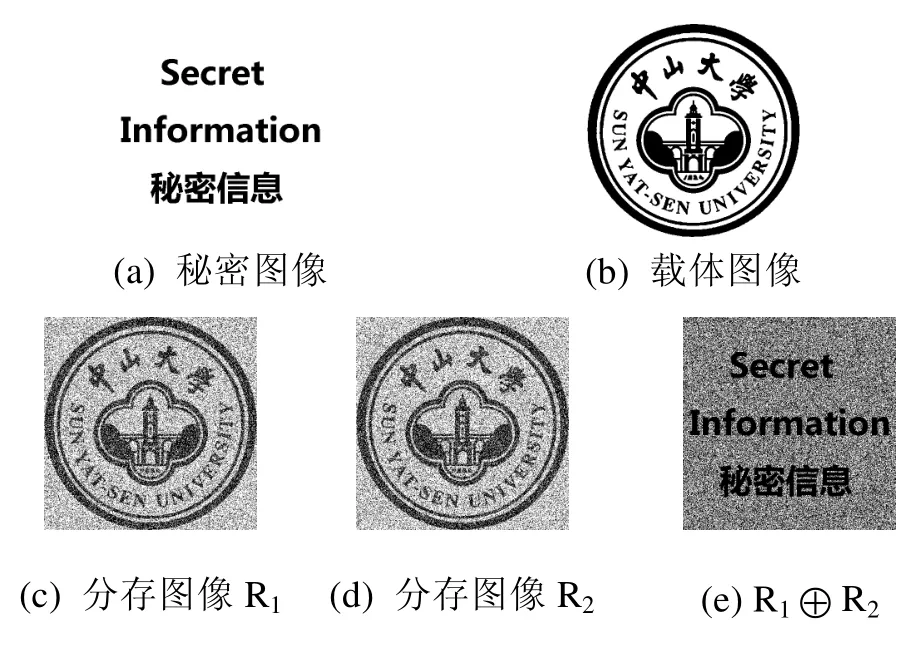
图1 算法2在(2, 2)方案的实验结果(β=0.5,图像大小512×512)

另一个实验是由算法3所生成的(2，3)异或图像分存方案，其中参数 n = 3,β = 0.75，见图2。同样的，生成的分存图像无法得到秘密图像的任意信息。但是，任意两幅分存图像的异或结果可以恢复出秘密图像的信息。

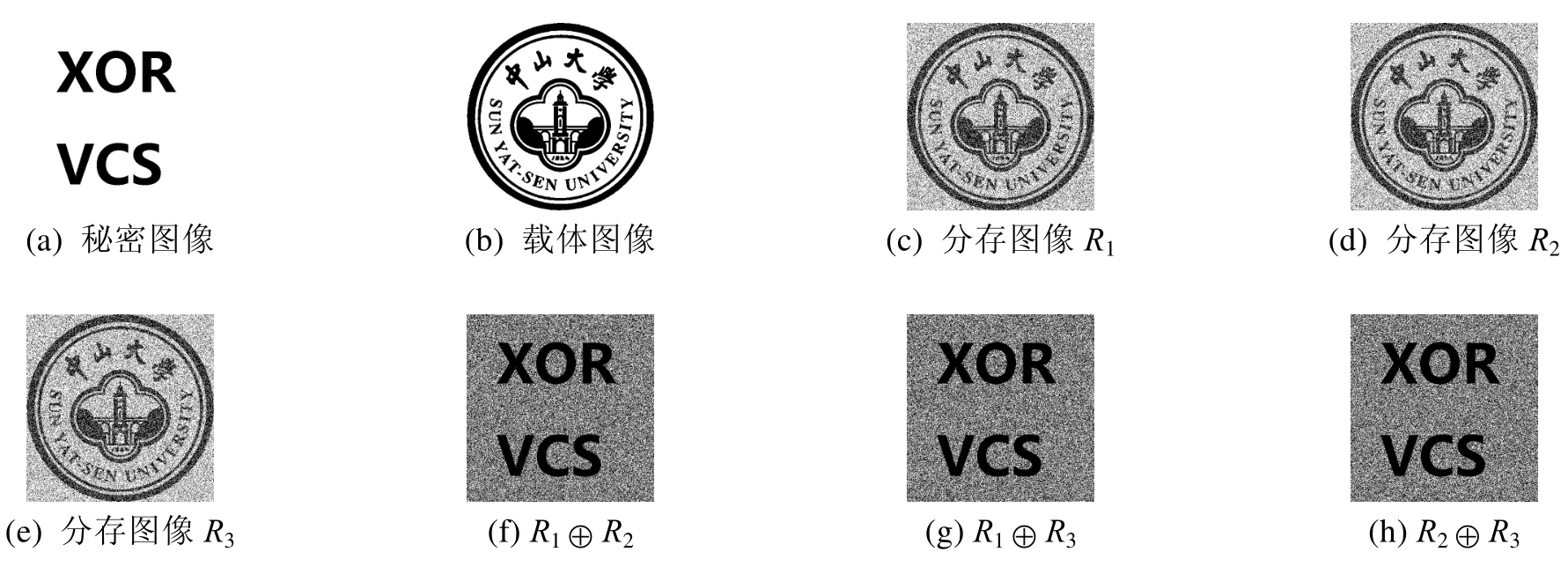
图2 算法3在(2, 3)方案下的实验结果(参数n = 3，β = 0.75时，图像大小为512×512)

3.2 理论结果的正确性

在上节中，可以得到有意义的(2, n)异或图像分存方案的理论对比度计算如下：

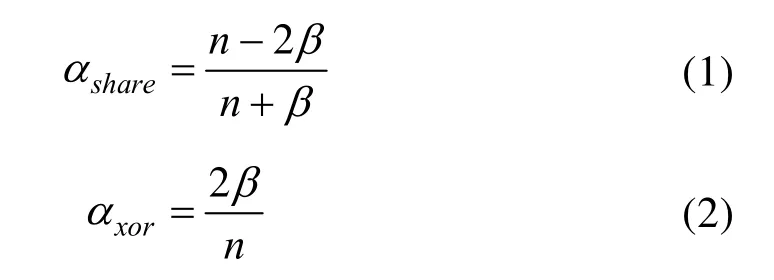
为检验以上对比度的正确性，需计算实验 2中(2，3)方案的实验对比度，见表 1。观察表 1，针对每幅分存图像 Ri，可以得到T( Ri[ S (1)]) ≈ T( Ri[ S(0)])且 T( Ri[ C (1)])＞ T( Ri[ C (0)])。这表明，分存图像是类似载体图像 C的有意义图像，但其不会得到秘密图像 S的任何信息，满足了安全性和有意义的两个条件。用 Rx⊕ Ry来表示任意两幅分存图像 Rx和 Ry的异或结果，可以得到：

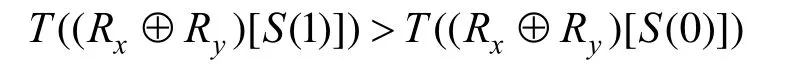
T((Rx⊕Ry)[C (1)]) ≈ T((Rx⊕ Ry)[C(0)])。这说明了任意两个分存图像的异或结果可以恢复出秘密图像却不会携带任何载体图像的信息，满足了对比度的条件。此外，不难发现 T((Rx⊕ Ry)[S(0)])恒等于0，这说明了黑色像素的重构是完美的。同时，根据等式(1)和(2)，可以计算在(2, 3)实验中恢复图像和分存图像的理论对比度分别为0.5和0.4。表1表明理论对比度和实验对比度的结果几乎是完全一致的。

3.3 方案比较

将本文的异或图像分存方案与相关分存方案进行比较，见表2。本文中异或图像分存方案的主要优点，总结如下：

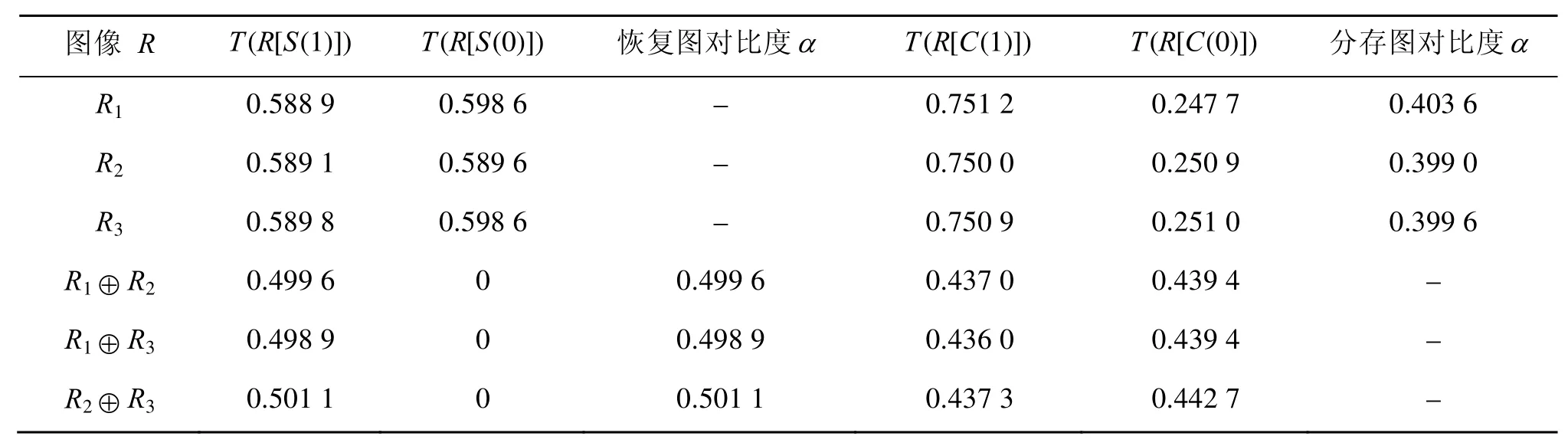
表1 (2,3)实验中恢复图像和分存图像的实验对比度

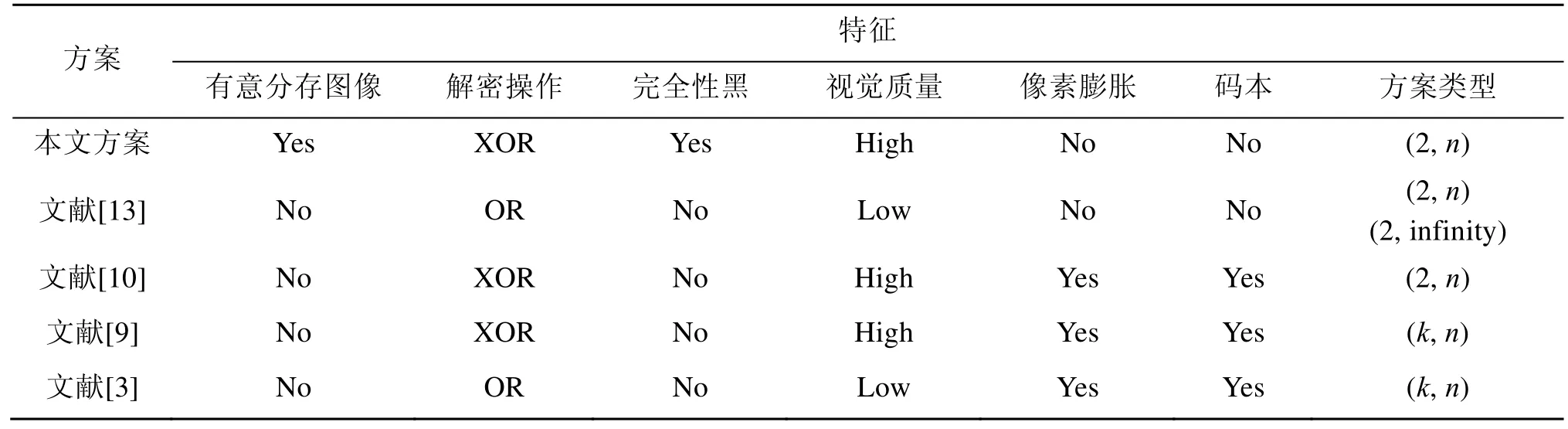
表2 本文方案与其他相关分存方案的特征比较

(1) 能够生成有意义的分存图像，且无需额外的隐藏处理过程。

(2) 秘密黑色像素的重构是完美的，有利于肉眼识别秘密图像。

(3) 与叠加的VC方案相比，可获得更好视觉效果的恢复图像和分存图像。

(4) 无需码本和无像素膨胀。

4 总 结

本文利用翻转操作构造(2, 2)和(2, n)异或图像分存方案。本文方案具有无需码本和无像素膨胀的优点，并能够在无需额外隐藏处理的情况下直接生成有意义的分存图像，以减少方案的计算时间。在解密过程中，只需要任意两个分存图像进行异或操作，其异或结果对秘密黑像素的重构是精准的。由于不同的参数可以得到不同视觉效果的分存图像和恢复图像，所以本文方案在应用上具有一定灵活性。理论分析和实验结果验证了本文方案的正确性和有效性。

[1]Blakley G R. Safeguarding cryptographic keys [C]//in Proc. AFIPS 1979, National Computer Conference, 1979: 313-317.

[2]Shamir A. How to share a secret [J]. Communications of the ACM, 1979, 22(11): 612-613.

[3]Naor M, Shamir A. Visual cryptography [C]//Advances in Cryptology EUROCRYPT'94. Springer Berlin Heidelberg, 1995: 1-12.

[4]欧锻灏, 孙 伟, 林 博. 一种新的基于可逆矩阵的具有完整性检验能力的图像加密方案[J]. 图学学报, 2012, 33(2): 89-92.

[5]易开祥, 孙 鑫. 一种基于混沌序列的图像加密算法[J].计算机辅助设计与图形学学报, 2000, 12(9): 672-676.

[6]Liu Feng, Wu Chuangkun. Embedded extended visual cryptography schemes [J]. IEEE Transactions on Information Forensics and Security, 2011, 6(2): 307-322.

[7]Shyu S J. Image encryption by multiple random grids [J]. Pattern Recognition, 2009, 42(7): 1582-1596.

[8]Chen T, Tsao K. Threshold visual secret sharing by random grids [J]. Journal of Systems and Software, 2011, 84(7): 1197-1208.

[9]Tuyls P, Hollmann H D, Van Lint J H, et al. Xor-based visual cryptography schemes [J]. Designs, Codes and Cryptography, 2005, 37(1): 169-186.

[10]Liu Feng, Wu Chuankun. Optimal xor based (2, n)-visual cryptography schemes [R]. IACR Cryptology ePrint Archive, 2010-10-25.

[11]欧锻灏, 吴小天, 孙 伟, 等. 基于恢复函数和误差扩散的灰度图像分存方案[J]. 计算机科学, 2013, 40(2): 112-116.

[12]吴小天, 孙 伟. 基于误差扩散的图像分存方案[J]. 计算机应用, 2011, 31(1): 74-77.

[13]Chen Shangkuan, Lin S J. Optimal (2, n) and (2, infinity) visual secret sharing by generalized random grids [J]. Journal of Visual Communication and Image Representation, 2012, 23(4): 677-684.

A (2, n) XOR-Based Secret Image Sharing Scheme Based on Flipping Operations

Ou Duanhao1, Wu Xiaotian1, Cheng Binyi2, Sun Wei2,3
(1. School of Information Science and Technology, Sun Yat-sen University, Guangzhou Guangdong 510006, China; 2. School of Software, Sun Yat-sen University, Guangzhou Guangdong 510006, China; 3. State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China)

A new method for constructing XOR-based secret image sharing scheme by flipping operations. The proposed scheme encodes a secret image in a perfect secure way without any knowledge of cryptography. The meaningful shares can be directly generated by the proposed scheme without any extra data hiding process. Meanwhile, neither pixel expansion nor extra codebook is needed in the proposed scheme. Further, the reconstruction of black pixels is perfect, which means all the revealed pixels associated to secret black pixels are always black. First, a meaningful (2, 2) XOR-based image sharing scheme is constructed by flipping operations. Subsequently, a meaningful (2, n) scheme is extended as well. Theoretical analysis and experimental results demonstrate the correctness and feasibility of the proposed scheme.

secret image sharing; flipping operation; meaningful shares; perfect black; XOR operation

TP 309.7

A

2095-302X(2015)01-0056-06

2014-08-11；定稿日期：2014-08-20

国家“973”计划资助项目(2011CB302400)；广东省自然科学基金资助项目(S2013010013728)

欧锻灏(1986–)，男，广东陆丰人，博士研究生。主要研究方向为多媒体信息安全、图像分存。E-mail：ouduanhao@163.com

孙 伟(1972–)，男，江苏连云港人，教授，博士。主要研究方向为信息安全、数字媒体。E-mail：sunwei@mail.sysu.edu.cn