基于匀质条带的矩形件最优三块布局算法
2015-03-15潘卫平陈秋莲崔耀东陈怡丹
潘卫平, 陈秋莲, 崔耀东, 陈怡丹
(广西大学计算机与电子信息学院,广西 南宁530004)
基于匀质条带的矩形件最优三块布局算法
潘卫平, 陈秋莲, 崔耀东, 陈怡丹
(广西大学计算机与电子信息学院,广西 南宁530004)
为解决大规模矩形件布局问题,提出一种动态规划算法生成基于匀质条带的矩形件最优三块布局方式。这种算法将板材分为三个块,同一块中只包含方向和长度均相同的匀质条带。通过求解背包模型生成块中的条带最优布局,隐枚举的讨论所有可能尺寸的块,确定所有三块组合的布局价值,选择布局价值最大的一个组合作为最优解。通过文献中的测题,将该算法与经典两段布局算法和启发式布局算法 TABU500进行比较。实验结果表明:该算法在计算时间和材料利用率两方面都有效,且生成的布局方式简化了下料切割工艺。
下料;三块布局方式;匀质条带;背包模型
切割与装填布局(cutting and packing, C&P)[1]问题是一个古老的著名问题,广泛存在于计算机科学、工业工程、逻辑学、制造业等领域。从数学和计算复杂性理论上看C&P是一类典型的NP难度问题[2-4],至今人们尚无法给出既完整、精确又快速、高效的求解方法。针对不同领域的应用需要,众多学者提出了相应的模型和算法[4-7]。特别是在制造业领域,随着资源和能源危机的出现,要求各企业提高原材料利用率、减少切割能源消耗,于是迫切需要人们研制出下料利用率高且切割工艺简单的布局优化算法。
本文讨论二维无约束剪切布局(unconstrained two-dimensional cutting packing, UTDCP)问题:将大板材L×W切割成m种小矩形件毛坯,第i种毛坯尺寸为 li×wi,价值为 ci(i=1,2,…,m)。对每种毛坯在板材中出现的次数无约束,布局目标是使得布局价值(板材中所含毛坯的总价值)最大。令R为一个布局方式,zi为此布局方式包含第i种毛坯的个数。优化模型为:

s.t. R满足剪切工艺要求。
与 UTDCP问题紧密相关的是二维剪切下料(two-dimensional cutting stock, TDCS)问题:将库存板材剪切出一定数量的若干种不同尺寸的矩形毛坯,优化目标是使得消耗的板材总面积最小。下料问题的解是由一组布局方式组成,每种布局方式由相应的UTDCP算法生成。经常采用线性规划(linear programming, LP)法求解TDCS问题。LP法通过反复迭代求解,每次迭代都需调用UTDCP算法生成一个新的布局方式。通常在LP法找到最优解之前,需要求解出几千个 UTDCP问题,一个UTDCP问题耗时一秒,求解TDCS问题需耗时几千秒[8]。因此UTDCP算法不仅要求布局价值较大,而且耗时短。
针对UTDCP问题的算法可以分为三类:①生成普通布局方式的精确算法[9];②生成普通布局方式的启发式算法,比如TABU500[10];③生成特定布局方式的确定性算法,比如两段布局算法[11]。
精确算法可生成最优普通布局方式,但其解决问题所耗费的时间是人们所不能容忍的[12]。启发式算法速度总体上比精确算法要快,但是其收敛速度未知,且无法保证解的质量。确定性算法是对生成的布局方式做一些特定限制,从而能在确定的较短时间内得到切割工艺简单、布局价值较高的布局方式。本文主要研究确定性布局算法。
文献[13]和[11]采用递归算法分别生成T型布局方式和两段布局方式。以上两种布局方式都是先将板材分成两段,然后在段上进行条带布局,各段的长宽固定了一个尺寸,其数值为板材的长或宽。段尺寸固定了一个指标势必降低了段的灵活度,制约了布局价值的提高。对文献[11]布局方式进行扩展,用两根互相垂直的分界线将板材划分成可以任意取值的三块。分析以上三种布局方式的几何性质可以得出:T型布局方式⊆两段布局方式⊆三块布局方式。故最优三块布局方式的价值在理论上大于等于最优两段布局方式的价值是确定的。
本文提出动态规划思想的确定性布局算法来生成新的布局方式——匀质条带三块布局方式(homogeneous three block strip, HTBS),并通过实验验证该布局算法(HTBSA)的有效性。
1 基本概念
1.1 条带
假定毛坯的方向固定。此假定并不影响本文算法的通用性,若允许毛坯转向,则可把毛坯 li×wi看作规格为li× wi和wi× li的两种毛坯。
一个或多个毛坯排成一行(列),称作条带。条带有普通条带和匀质条带两种类型,如图1所示,数字表示毛坯编号。普通条带可含多种毛坯,匀质条带只含一种毛坯。匀质条带利用率比普通条带利用率稍低,但切割工艺比较简单。

图1 条带
1.2 匀质条带三块布局方式
三块布局方式首先用一条主分界线将板材分为两个块,然后用一条辅分界线将其中的一块再划分为两个块。如图 2所示,当主分界线是竖直线时,称为X向三块布局方式;当主分界线是水平线时,称为Y向三块布局方式。每个块里面只包含方向和长度均相同的匀质条带。块的方向由块中条带的方向决定,当条带方向是水平时称为X向块;当条带方向是竖直时称为Y向块。图3是一个X向三块布局方式图(布局同图2(a)),A块里面包含1号、7号、19号三条水平条带;B块包含一条22号水平条带;C块里面包含两条24号、一条26号、一条30号竖直条带。
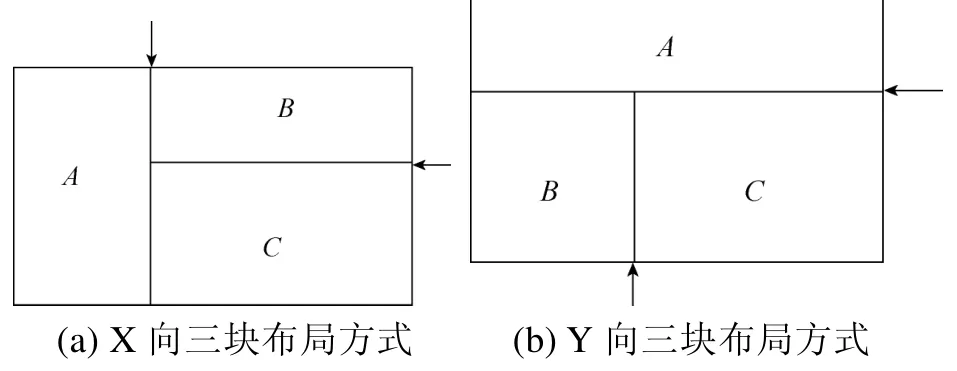
图2 三块布局方式的类型
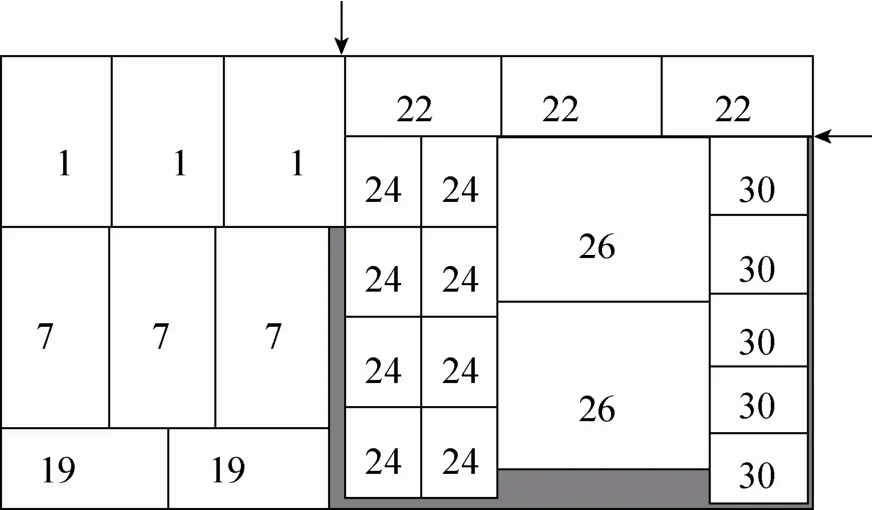
图3 三块布局方式图
2 算法原理及其实现
假设板材的尺寸和毛坯的尺寸都为整数,毛坯不允许转向。对于规格为L W× 的板材,假定L W≥ 。现介绍生成最优HTBS布局方式的方法,包含以下步骤:①求解条带的价值;②确定条带在块中的最优布局;③确定最优三块布局方式。
2.1 求解条带的价值
令 n(i,x) i x为水平条带ix w× (长:x,宽:iw)中所含毛坯的个数, s(i,x)为条带的价值,则有如下公式:
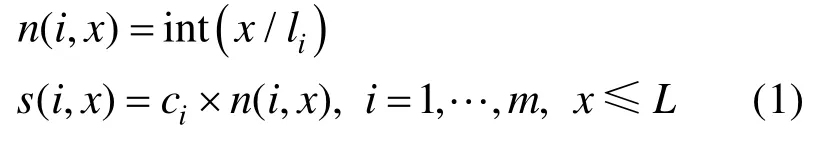
对于竖直条带可以类似的确定其价值 s( i, y)。
2.2 确定块中条带的最优布局
对于块x × y(长:x,宽:y),记 f( x, y)为块的价值,x ≤ L,y ≤ W。对X向块,令 zX(i, x)为块中包含水平条带 x × wi的个数, fX(x, y)为块价值;对Y向块,令 zY(i, y)为块中包含竖直条带 y ×li的个数, fY(x, y)为块价值。则有如下公式:

上述模型是典型的背包问题,可用动态规划方法求解。因为动态规划方法具有全容量性,所以当求解出 f(L,W) 后,其他的y W≤ 均可得知。
2.3 确定最优三块布局方式
用XV,YV分别表示最优X向三块布局方式与最优Y向三块布局方式的价值,V为最终的三块布局方式价值。则有如下公式:
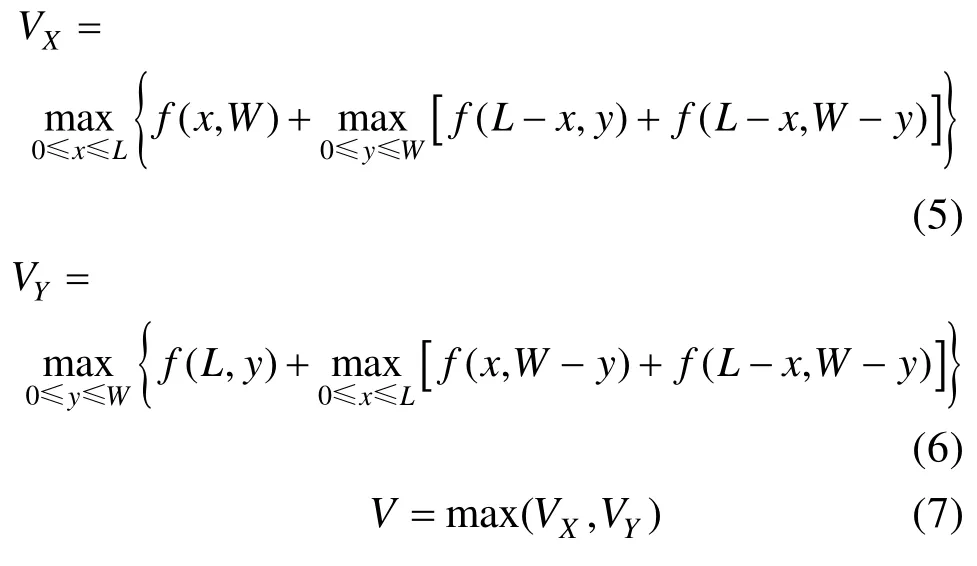
式(5)中x为主分界线位置,y为辅分界线位置。其中x,y均为整数。
式(6)中y为主分界线位置,x为辅分界线位置。其中y,x均为整数。
式(7)说明选择X向三块方式和Y向三块方式中价值较大的作为最终的三块布局方式。
2.4 三块布局算法的时间复杂度
式(1)求解条带价值时间复杂度为 O( m L)。式(2)~(4)求解块价值时间复杂度为 O( m WL)。式(5)~(7)确定最优三块布局方式时间复杂度为 O( W L)。
综上得出:三块布局算法总的时间复杂度为O( mWL)。
3 实验结果
用C#语言实现本文算法,在主频为2.7 GHz,内存为2 GB的计算机上进行实验。通过文献中的基准测题,将本文算法分别与两段布局算法和启发式布局算法TABU500进行比较。
3.1 第一组测题的实验结果
采用文献[11]Table 4的6道测题,板材规格均为3 000×1 500,毛坯的价值等于其面积。对于每道测题,文献[9]中算法可生成最优普通布局方式,文献[11]中算法可生成最优匀质条带两段布局方式,本文算法生成最优匀质条带三块布局方式。设v1、v2、v3,t1、t2、t3分别为以上三种算法的布局方式价值和所花的计算时间(s)。表 1为测题的实验结果。图4为本文算法生成的测题5的布局方式图。
从表1可以看出在6道测题中,本文算法优化结果有4道测题好于两段布局算法(用“+”标记),其余2道等于两段布局算法(用“=”标记)。本文算法计算时间和两段布局算法相当,在实际应用中合理。
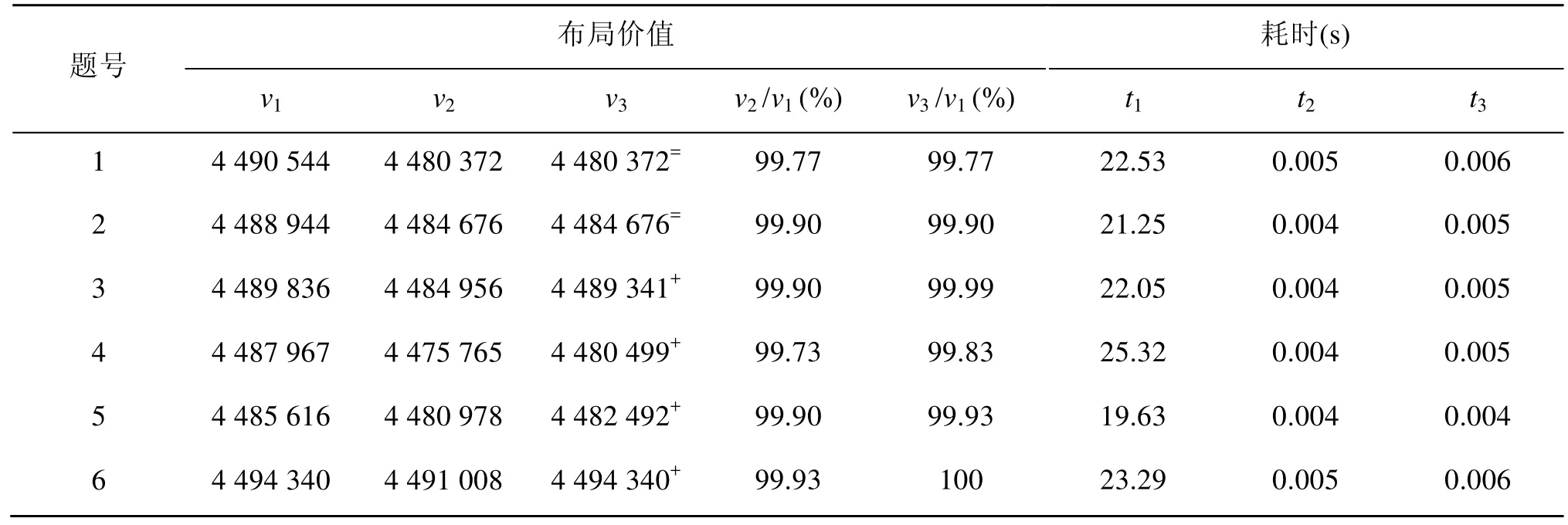
表1 第一组测题的实验结果(6道测题)

图4 测题5的布局方式图
3.2 第二组测题的实验结果
本节包含20道规模较大的布局测题,参考文献[10]。其中前 10道测题,毛坯的价值即为其面积,后10道测题毛坯的价值和其面积是独立的。设文献[9]精确算法得到的布局方式价值为 v1、文献[10]启发式算法TABU500得到的布局方式价值为 v2、本文算法得到的布局方式价值为 v3。表 2为三种布局方式价值的比较结果。
在 20道测题中,本文算法的优化结果有 13道测题好于 TABU500(用“+”标记),有 4道等于TABU500(用“=”标记),有3道差于TABU500(用“–”标记)。本文算法平均布局价值为 4 426 952,TABU500平均布局价值为4 413 688。本文算法布局价值总体上高于TABU500。
TABU500解决20道测题耗时218 s,平均每道测题计算时间为10.9 s。本文算法解决20道测题总共耗时0.46 s,平均每道测题计算时间为0.023 s,计算时间只有TABU500算法的0.21%。图6给出了本文算法生成的测题APT16和APT20的布局方式图。
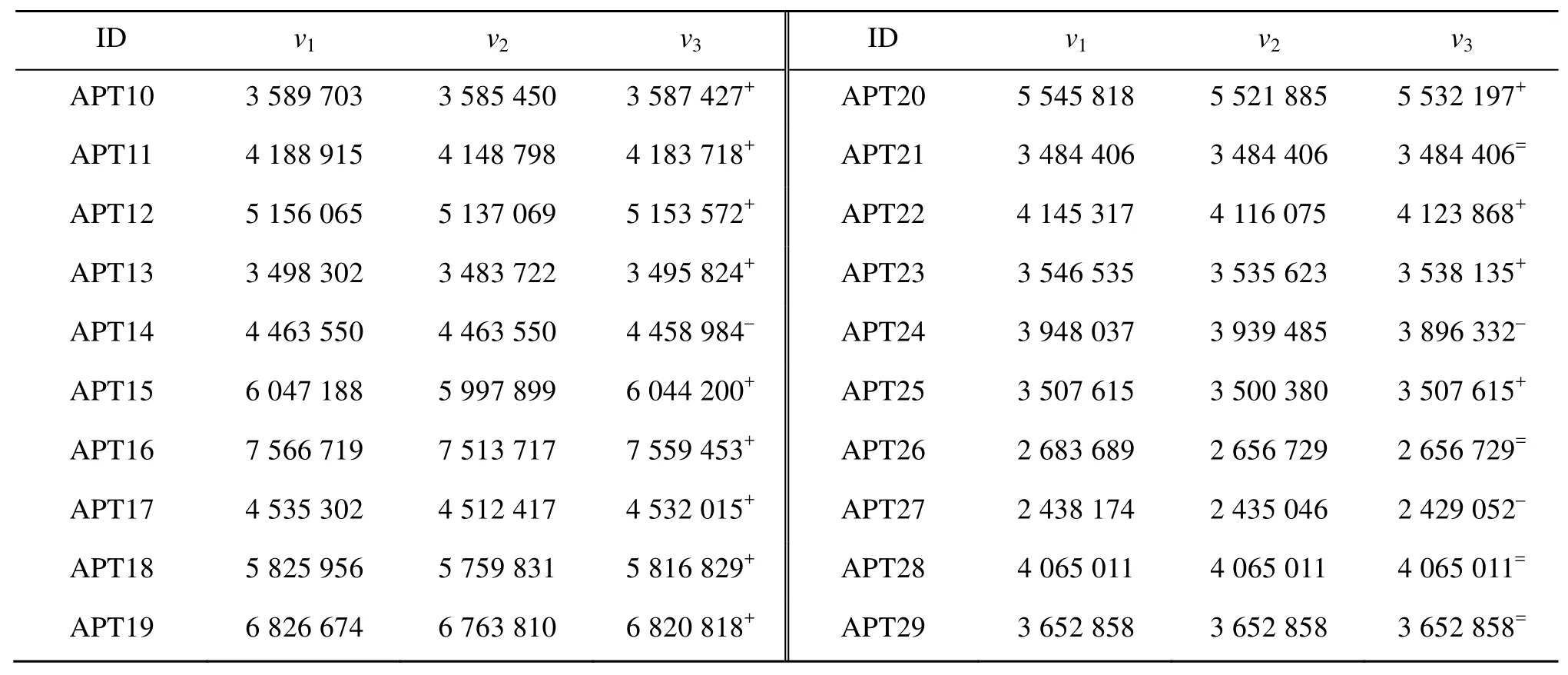
表2 第二组测题三种布局方式价值比较结果(20道测题)
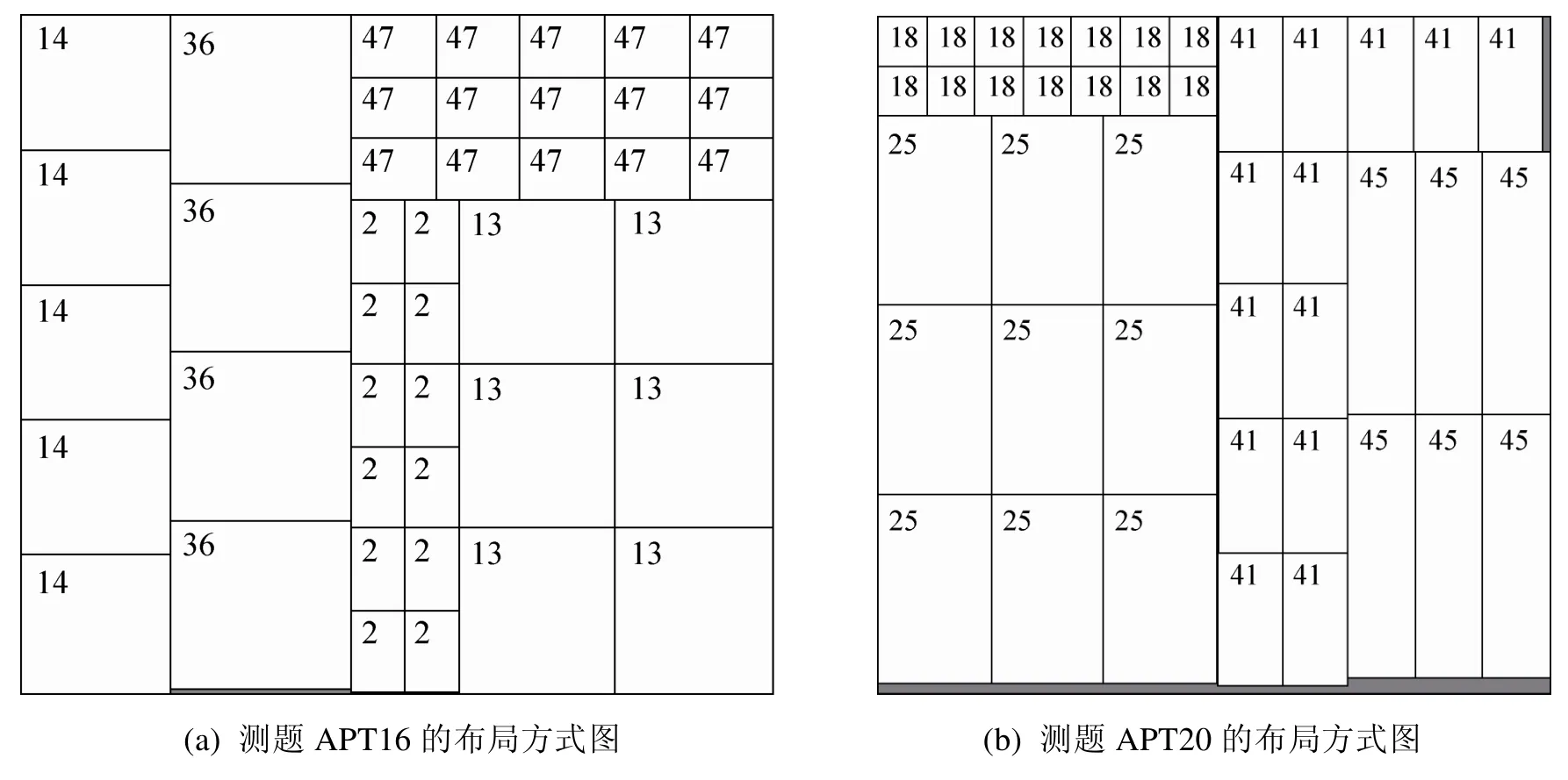
图5 测题APT16和APT20的布局方式图
4 结 束 语
本文讨论了矩形件无约束两维布局问题。提出了一种新型布局方式——HTBS布局方式,并采用HTBSA算法来生成此种布局方式。该布局方式切割工艺比较简单,能够提高下料效率节省切割能耗。HTBSA算法其平均布局价值高于两段布局算法和TABU500。将本文算法和线性规划法相结合,可以较好地解决TDCS问题。
[1]Wäscher G, Haußner H, Schumann H. An improved typology of cutting and packing problems [J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.
[2]郑荣杰, 张鹏程, 崔海良, 等. 基于蒙特卡罗方法的矩形布局问题研究[J]. 图学学报, 2012, 33(4): 33-36.
[3]王金敏, 王保春, 朱艳华. 求解矩形布局问题的自适应算法[J]. 图学学报, 2012, 33(3): 29-33.
[4]何 琨, 黄文奇, 金 燕. 基于动作空间求解二维矩形Packing问题的高效算法[J]. 软件学报, 2012, 23(5): 1037-1044.
[5]张德富, 彭 煜, 张丽丽, 等. 求解三维装箱问题的混合模拟退火算法[J]. 计算机学报, 2012, 35(12): 2553-2561.
[6]Cui Yaodong. Heuristic for the cutting and purchasing decisions of multiple metal coils [J]. Omega, 2014, 46: 117-125.
[7]Furini F, Malaguti E. Models for the two-dimensional two-stage cutting stock problem with multiple stock size [J]. Computers & Operations Research, 2013, 40(8): 1953-1962.
[8]Cui Yaodong. A new dynamic programming procedure for three-staged cutting patterns [J]. Journal of Global Optimization, 2013, 55(2): 349-357.
[9]Wang Z, Li J, Cui Y. Exact and heuristic algorithms for staged cutting problems [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2005, 219(2): 201-207.
[10]Alvarez-Valdés R, Parajón A, Tamarit J M. A tabu search algorithm for large-scale guillotine (un) constrained two-dimensional cutting problems [J]. Computers & Operations Research, 2002, 29(7): 925-947.
[11]Cui Yaodong, He Dongli, Song Xiaoxia. Generating optimal two-section cutting patterns for rectangular blanks [J]. Computers & Operations Research, 2006, 33(6): 1505-1520.
[12]季 君, 陆一平, 查建中, 等. 生成矩形毛坯最优两段排样方式的确定型算法[J]. 计算机学报, 2012, 35(1): 183-189.
[13]崔耀东. 生成矩形毛坯最优T型排样方式的递归算法[J]. 计算机辅助设计与图形学学报, 2006, 18(1): 111-114.
An Algorithm for Generating Optimal Homogeneous Strips Three Block Patterns of Rectangular Blanks
Pan Weiping, Chen Qiulian, Cui Yaodong, Chen Yidan
(Computer and Electronic Information College, Guangxi University, Nanning Guangxi 530004, China)
With the purpose of solve the large scale rectangular blanks packing problem, a dynamic programming algorithm for generating the optimal homogeneous strip three block layouts is presented. The plate is divided into 3 blocks, and every block contains only uniform strips which have the same direction and length. The knapsack model to generate the optimal strip layout on the block is firstly solved, and all possible sizes of blocks through implicit enumeration are discussed. All three block layout value is determined, and a layout of the maximum value is selected as the optimal solution. The algorithm was tested on some problems in the literature, and compared with the two algorithms which are classical two segment layout algorithm and heuristic algorithm of TABU500. The experimental results show that the algorithm not only can improve the utilization rate of material, but also has a reasonable computation time and can simplify the cutting process.
stock packing; three block patterns; homogeneous strip; knapsack model
TH 164;TP 301.6
A
2095-302X(2015)01-0007-05
2014-07-18;定稿日期:2014-09-16
国家自然科学基金资助项目(61363026,71371058);广西省自然科学基金资助项目(2014GXNSFAA118357)
潘卫平(1989–),男,湖北武穴人,硕士研究生。主要研究方向为优化计算与CAD技术。E-mail:1102358841@qq.com
