基于分层图像复原的水下目标距离估计❋

王 蕊， 王国宇， 姬婷婷， 杨 雪，3

(1. 中国海洋大学，山东 青岛 266100； 2. 滨州医学院， 山东 烟台 264003； 3. 青岛农业大学，山东 青岛 266109)



基于分层图像复原的水下目标距离估计❋

王 蕊1，2， 王国宇1， 姬婷婷1， 杨 雪1，3

(1. 中国海洋大学，山东 青岛 266100； 2. 滨州医学院， 山东 烟台 264003； 3. 青岛农业大学，山东 青岛 266109)

水下目标的距离估计对于水下作业有着十分重要的意义。目前常用的距离估计方法无论是光测距还是声测距都对于设备有很大的依赖性，本文提出一种基于复原技术的距离估计方法，通过建立水下退化图像的分层复原模型并利用清晰度评价函数，根据对图像清晰复原时的参数估计实现目标距离估计。这种方法紧需要单幅水下图像就可实现目标整体距离估计。文中通过实验验证了该方法的有效性。

水下图像；水下测距；分层复原；图像复原；水下退化函数

水下目标的距离信息对于水下观测、目标定位、水下机器人作业等都具有重要意义。传统测距可以大致分为主动测距和被动测距[1]：主动测距是指发射器主动发出特定形式光波或声波，通过对其在水中传播时遇到目标物体反射回波的分析得到距离信息，典型的如声纳测距、激光测距和结构光测距等，其缺点是成本高，对设备依赖性高。在光学传感领域，计算机视觉的发展为被动测距提供了更多的技术实现，得到越来越多的研究。基于计算机视觉的被动测距方法主要有双目视觉法、运动三维检测、结构光法和单目视觉法等。双目视觉法[2]是通过两个或多个摄像镜头获得目标背景相同的多幅图像，通过确定某一点在两幅图像中的位置相同，再根据其他特征在图像中的不同位置找到匹配的特征点的位置。运动三维检测[3]是以时间和空间为坐标，通过获取坐标系中的一系列图像，并对这些图像进行分析，找到图像中的匹配特征点，以此求取物体的深度信息。结构光测距[4]是基于双目测距原理发展而来，双目使用的是物体本身的特征点，而结构光使用的是光源主动提供的特征点，因此不需要根据场景的变化而变化，降低了匹配的难度。但是这3种被动测距方法都需要获得不止一幅图像，实时性较差。单目视觉法[5]仅需要单一摄像头拍摄的单幅图像，通过模拟人类视觉，根据特征变化、整体环境或目标模糊程度判断目标的深度信息。基于特征和环境分析的单目测量需要采集大量图像来训练完善模型，最终实现深度匹配。而目标的模糊程度可以通过图像的退化机制反演估计得到，所以图像的退化函数对于估计距离信息十分重要。

水下图像的退化函数除了和深度相关，还与水体介质的特性有关，目前的水下图像退化函数估计方法[6-7]都需要先测量水体参数。本文提出了一种基于分层图像复原技术的距离估算方法，通过分层模型描述水下目标成像时的退化过程，然后利用无穷远处的水体图像分析得到退化参数，并以此分层复原图像达到最清晰时的退化参数即对应实际成像中的水体距离。文中对清晰度评价方法进行了实验分析，通过不同距离成像时的复原结果与实际测距对比，验证了所提方法的有效性。

1 水下退化图像的分层复原方法

水下图像的退化由衰减和散射2部分引起：衰减造成图像发暗，可以通过亮度补偿的手段来弥补；散射造成图像的模糊退化，表现为细节丢失、对比度下降，其中前向散射为沿目标反射光线传播方向的散射，造成图像的弥散模糊；后向散射会增加背景噪声和雾化作用。

假设由于整个目标与接收器之间的水体的衰减和散射所造成图像退化的点扩散函数为h(x,y)， 清晰目标图像为f(x,y)，接收器所得到的退化图像为g(x,y)，水体中由于后向散射引起的加性噪声为n(x,y)，图像的退化模型为：

g(x,y)=f(x,y)*h(x,y)+n(x,y)。

(1)

点扩散函数h(x,y)和后向散射噪声n(x,y) 不仅与水体光学性质有关，也与水体的散射体积有关。为了定量描述h(x,y)以及噪声统计特性与水体长度的关系，我们提出一种散射介质的分层退化模型[8]，将目标与接收器之间的水体分层为各个独立的退化单元，并将各单元的退化传输视为各个线性子系统的输出。对独立的退化单元建立PSF模型，在此基础上对h(x,y)和噪声统计特性给出了参数化描述。图1为水体退化模型的分层分解示意图(见图1)：

图1 分解后的水体退化模型Fig.1 Layered decomposition of the water between the target and the sensor

沿着成像传感器的光轴(用z轴表示)把水体平均分为m层，每层的厚度用 ( 表示(( 足够小)。当光在水中传输时，每层水体作为一个独立的线性传输单元，光在其中传播时会产生前向散射和后向散射，因此整个散射介质的点扩散函数可被描述为连续线性子系统的组合。设每一层的点扩散函数为hε，那么整个水体的点扩散函数为：

h=hnε.=hε.(1)×hε.(2)×hε.(m)。

(2)

假设每一层上的前向散射是由大量独立分布的悬浮粒子的散射叠加而成，根据中心极限定理，我们用高斯分布模型来描述每一单元层的点扩散函数hε(x,y)：

(3)

其传递函数形式为：

Hε(u,v)=e(-aεπ(u2+v2))。

(4)

定义单位厚度模型参数ρ=aε/ε；则(4)式可以写为：

Hε(u,v)=e(-ρεπ(u2+v2))。

(5)

根据图1，对于长度为z的水体，z=mε；由(2)式可以得到长度为z的水体的点扩散函数为：

Hz(u,v)=e(-ρz(u2+v2))。

(6)

考虑到反射光的衰减，c为衰减系数，则有：

Hz(u,v)=e(-ρz(u2+v2))e(-cz)=
e(-z(ρ(u2+v2)+c)=e(-cz(ρ/c×(u2+v2)+1))。

(7)

设I是距离z处的光照强度，定义k(x,y)是单位长度后向散射系数，那么对于距离z处厚度为dz的水层所引起的退化为：

dnz(x,y)={k(x,y)Idz}×hz(x,y)。

(8)

令k(x,y) =k0+ γ，其中k0表示直流分量，γ表示方差为σ2的噪声分量。当环境光照明时，水体各处的照明强度相同，即I=I0(常数)。将(8)变换到频域并积分，得到后向散射的直流分量Sd和噪声分量的功率谱Pn(u,v)：

Sd=(kI0/c){1-exp(-cz)}。

(9)

(1-exp{-[cz+zρπ2(u2+v2)]})2。

(10)

若使用主动照明方式并假设光源沿z方向照射目标，则有I=I0e(-cz)(I0是光源处的光强)，这种情况下，积分后(9)和(10)式中的参数c用2c替换。

选取图像中没有目标的区域计算后向散射噪声的功率谱Pn(u,v)，此时z→∞，与(9)和(10)式拟合可以求出参数I0k0/c、I0σ2/c和ρ/c的值。根据(7)式，当得到ρ/c的值后，式7就仅剩下cz一个未知量。分层退化模型将前向散射与后向散射的作用显式联系起来，使得描述前向散射的点扩散函数中的固有光学参数可以从后向散射噪声的统计计算中得到。如果cz也能够确定，则可以应用图像复原方法恢复目标的清晰图像。

根据公式(1)的频域表达式，本文采用常用的频域维纳滤波器，其表达式如下：

(11)

其中：F(u,v)为复原图像f(x,y)的频域表达式；Hz(u,v)为公式(7)；Pn为公式(10)；Pf为退化图像g(x,y)。

减掉后向散射噪声Sd后的功率谱，G(u,v)为退化图像g(x,y)的频域表达式。

由于整个散射介质的点扩散函数可被描述为连续线性子系统的组合，而每一个子退化系统的点扩散函数对应一个特定的水体厚度Δz，因此，可以沿着退化的反方向，对图像采用一系列不同层厚的cz进行复原，当复原到图像最清晰时对应的cz值，就是目标所在位置的光学距离。

为验证模型推导的正确性，本文进行了模拟实验：实验在室内水槽中进行，水槽中混合少量泥沙，由环境光自然照明，为了提高目标成像的可见度，在狭缝背面增加了背景照明以增加狭缝的亮度。分别获取狭缝距离为6、 8、 10、 …32、 34、 36cm的图像(见图2)。

由图2可以看出，随着距离的增加，后向散射噪声越来越明显，甚至淹没了信号。当使用频域维纳滤波器来对退化狭缝图像进行复原。

图2 狭缝图像距离相机分别为6、8、10、 …28、34、36cmFig.2 Slit images with distances of 6、 8、 10…32、 34、 and 36cm respectively

2 图像清晰度评价方法

由(11)式中根据G(u,v)求得F(u,v)得到对应的光学距离，实现准确估计的关键是选择合适的图像清晰度评价函数，要求清晰度评价函数满足灵敏度高、单峰性强、抗噪声干扰能力强的特点。常用的清晰度评价函数有：

(1)图像峰值信噪比[9](PSNR)，反映的是图像信噪比变化情况的统计平均，它是目前广泛应用的衡量图像主观质量的方法。当待评价图像g有标准的清晰图像f作为参考时，PSNR越大，说明图像g与参考图像f越接近，图像质量就越好，通常由2个图像的均方差(MSE)进行定义:

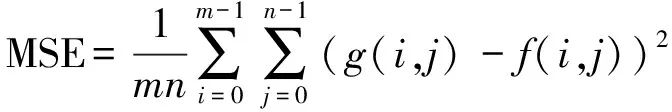
(12)

(13)

(2)图像灰度梯度向量模方和函数[10](SMD)，图像灰度的梯度函数常被用来提取边缘信息。图像越清晰，边缘也越尖锐，图像梯度函数值越大。所以可以用图像灰度梯度作为清晰度评价函数。由于梯度有方向性，所以使用梯度函数的平方和的均值作为评价：

[g(x,y+1)-g(x,y)]2)/mn。

(14)

(3)图像拉普拉斯和函数[11](LS)，常用作图像边缘的检测，图像越清晰，边缘越突出，拉普拉斯和函数值越大，其定义如下：

(15)

(4)熵函数法[12]是根据香农信息论而来的，熵越大时信息量越多，将此原理应用到图像清晰度评价，当图像能量一定时，图像的熵越大越清晰。熵函数的定义如下：

(16)

本文中的实验目标是双狭缝，其清晰图像可以描述脉冲函数图像。图3(a)为构造狭缝目标的模板图像，以它作为标准参考图像来验证复原图像的清晰度。(b)、(c)、(d)分别是复原不足的结果、复原合适的结果以及过复原的结果。

图3 狭缝复原结果比较

本文选取了图2中的12cm处图像和24cm处图像进行了实验，比较第2章中几种不同的清晰度评价函数有效性。每一幅图像都选取cz(层厚)分别为0.1、0.2、0.3、0.4……来进行复原，然后测量该幅图像的一系列不同复原图像的清晰度。

为了减少噪声的影响，选取局部图像进行评价，即截取一段狭缝图像作为评价区域。由于熵函数法要求图像能量不变，但是狭缝处有附加光源，在复原补偿了衰减光照导致能量增大，因此只比较PSNR、SMD和LS评价函数3种方法。

实验得到12cm处退化图像复原结果清晰度评价的随着cz变化的曲线分别如图4(a)、(b)和(c)表示；24cm处退化图像复原结果清晰度评价的随着cz变化的曲线分别如图5(a)、(b)和(c)表示:

实验结果表明PSNR和SMD很好地满足了清晰度评价函数的特性，而且可以分别作为有参考图像和无参考图像时的收敛准则。PSNR是目前广泛应用的图像清晰度评价函数，文中实验选取了狭缝图像，其清晰的可参考图片容易构造，因此使用局部峰值信噪比作为判断满足收敛的评价函数。

3 实验结果

采用经典的维纳滤波方法对图2中的一系列不同距离的退化图像进行复原，以PSNR作为清晰度评价准则。

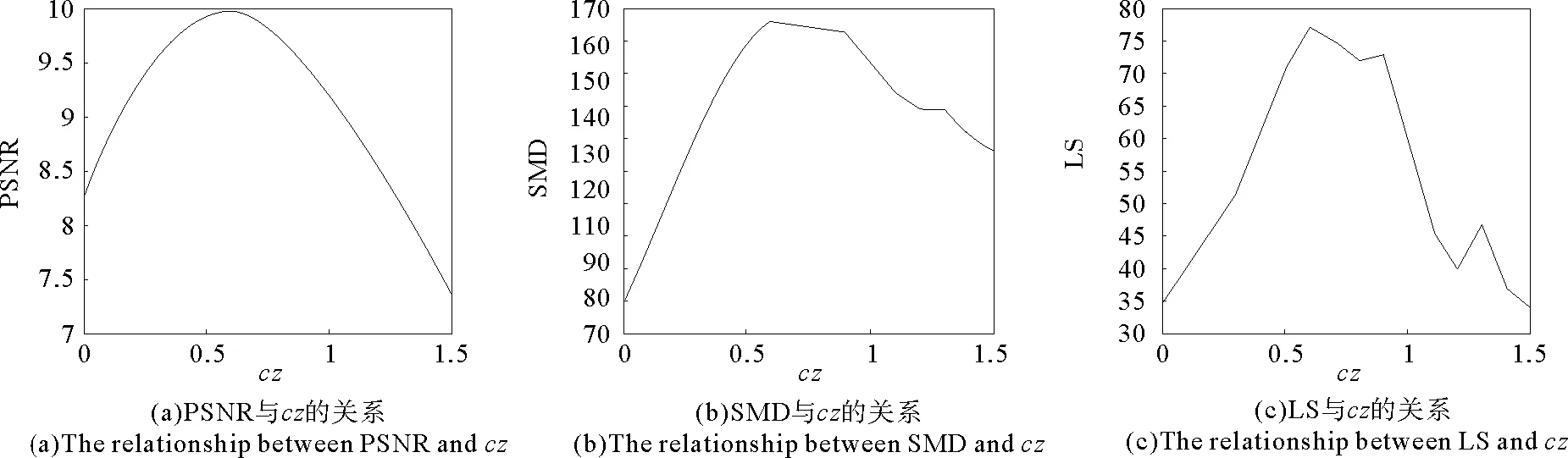
图4 12 cm处退化图复原结果清晰度Fig.4 Evaluation of the results of the degrade image at 12 cm

图5 24 cm处退化图复原结果清晰度Fig.5 Evaluation of the results of the degrade image at 24 cm

在测量光学距离cz时，可以先选用大步长，当接近收敛之后再使用小步长。当cz的数量级过大，图像会过复原，如图3(d)所示；当cz数量级过小，图像复原几乎没有效果，如图3(a)所示。选取cz较为合适的起始值，然后以合适的步长来增加cz直到复原达到PSNR最大时的最优结果，我们认为此时的cz就对应了真实的目标距离，如图3(c)所示。cz=0时的图片就是原始得到的退化图像。

下面以12cm处的图说明测量光学距离cz的过程：

步骤1 选取起始的cz=0，步长为0.1，图6中(a)～(d)分别表示当cz对应取0.1,0.3，0.5,0.7时的复原结果，表1为对应的峰值信噪比, 当cz=0.5时收敛；

步骤2 如表1所示对于步长是0.1时，最优的结果出现在峰值信噪比最大的第五步(即此时的cz=0.5)，当采取更小的步长来测量光学距离时，这个结果应当会出现在0.5的附近。因此我们选择从cz=0.5开始，步长缩小到0.01，如果峰值信噪比不升反降，则说明更精确的收敛结果在0.4～0.5之间，调整从cz=0.4开始，然后继续。表2步长0.01时各对应的峰值信噪比，当cz=0.55时收敛；

步骤3 重复步骤2，选取更小的步长进行复原。当cz=0.549时收敛。

图6 cz起始为0，步长为0.1时的收敛过程，(c)为收敛结果，此时峰值信噪比最大

按照上述步骤对图2中的不同距离处退化狭缝图像进行复原并达到收敛，表3为不同距离的狭缝图片对应的收敛时的光学距离cz。图7为光学距离cz与实际距离z的关系。

表1 cz步长为0.1的各复原结果对应峰值信噪比

表2 cz步长为0.01的各复原结果对应峰值信噪比

表3 图2中各个图片达到最优复原结果时对应的cz Table 3 The values of cz of best recovered results from Fig 3 /cm

由于c是常数，所以cz是z为正比例函数，图7说明实际复原测量出的光学距离与实际距离满足线性正比例关系，如果预先知道或现场测得环境水域的衰减常数c，则可以求出实际距离z。实验结果验证了所提出的基于图像分层复原的距离估计方法是有效的,同时也验证了所提出的理论模型的正确性。

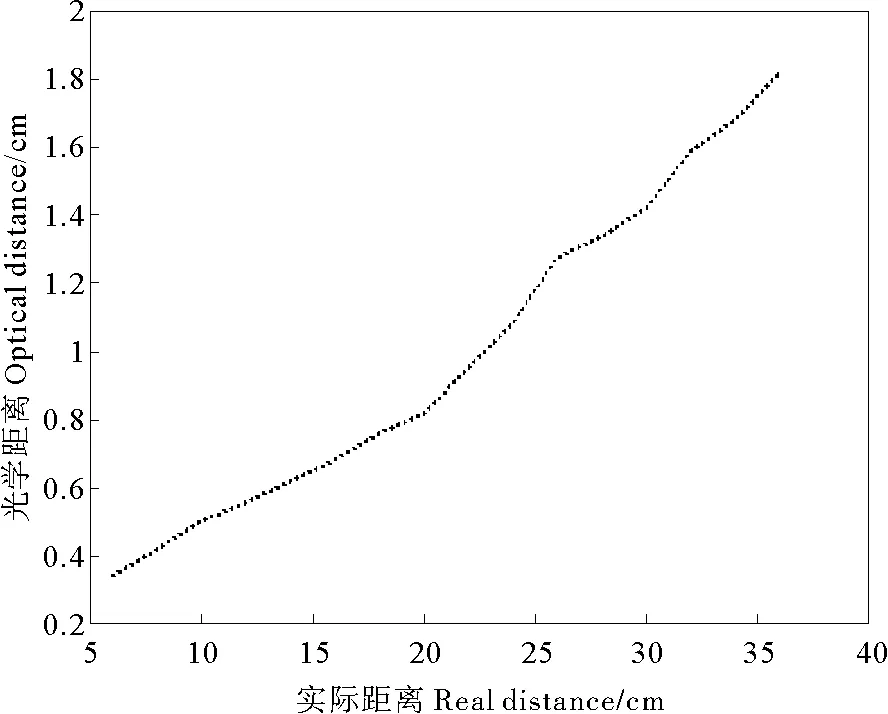
图7 光学距离cz与实际距离z的关系

4 结语

本文提出了一种基于单幅图像的水下目标测距方法，通过建立水下退化图像的分层复原模型并利用清晰度评价函数，根据对图像清晰复原时的参数估计实现了目标距离估计。其优势在于不需要高成本的三维测距设备，即可方便灵活地估计出水下目标的相对距离。由于小型潜器在水下探测任务中得到越来越多的应用，所携带的视觉系统的功能和重要性也受到越来越多的关注，所以该方法在水下导航、目标识别、机器人手眼操作等方面具有很大的应用前景。基于图像分层复原实现测距的理论依据利用了散射介质中成像时的扩散效应与传输距离的内在关系，算法实现的关键是对扩散模糊的传递函数进行恰当的描述。文中的实验结果证实所提出的分层点扩散函数模型是有效的。

未来还需要进一步对不同水体介质、不同浑浊程度的水下环境中点扩散函数的优化和改进做更深入的研究。

[1] Akbarally H, Kleeman L. 3D robot sensing from sonar and vision [C]. IEEE International Conference on Robotics and Automation. Minneapolis， Minnesota: [s.n.].1996: 686-691.

[2] Kenneht R, acstlemna, 数字图像处理[M]. 朱志刚,等译. 北京: 电子工业出版社， 2002: 165-167.

[3] Hopkins H H, The frequency response of a defocus optical [J] Proc Royal Soc, 1955, A231: 91-103.

[4] Valkenburg R J, McIvor A M. Accurate 3D measurement using a Structured Light System [J]. Image and Vision Computing, 1996, 16: 99-110.

[5] 黄桂平， 李广云， 王保丰, 等. 单目视觉测量技术研究 [J]. 计量学报， 2004, 25(4): 314-317.

[6] Mertens L E, J Replogle F S. Use of point spread and beam spread functions for analysis of imaging systems in water [J]. Opt Soc Am, 1977, A 67: 1105-1117.

[7] Hou W L, Gray D J, Weidemann A D, et al. Comparison and validation of point spread models for imaging in natural waters [J]. Optics Express, 2008, 16(13): 9958-9965.

[8] Wang G, Zheng B, Sun F F. Estimation-based approach for underwater image restoration [J]. Optics Letters, 2001, 36(13): 2384-2386.

[9] Huynh-Thu Q, Ghanbari M. Scope of validity of PSNR in image/video quality assessment [J]. Electronics Letters, 2008, 44 (13): 800.

[10] 曹茂永， 孙农亮, 郁道银.基于灰度梯度的数字图像评价函数[J]. 光电工程， 2003, 30(4): 69-72

[11] Feynman R, Leighton R, Sands. The Feynman Lectures on Physics [M]. 李洪芳， 译. 上海： 上海科学技术出版社, 2013.

[12] Jarvis R A. Focus optimization criteria for computer Image Processing [J]. Microscope, 1976, 24(2): 163-180.

责任编辑 陈呈超

Underwater Distance Estimation Based on Layered Image Recovery

WANG Rui1，2， WANG Guo-Yu1， JI Ting-Ting1, YANG Xue1，3

(1. Ocean University of China, Qingdao 266100， China; 2.Binzhou Medical University, Yantai 264003, China; 3. Qingdao Agricultural University, Qingdao 266109， China)

Depth information of objects underwater is very important for underwater operation. Instead of highly depending on equipments by the methods both light ranging and sound ranging, this paper proposed an underwater ranging method based on image recovery technology, which relies on estimating depth parameter in the underwater layered degraded function. This method requires single image rather than multi images. meanwhile, the experiments have been carried out to prove the effect of this method.

underwater image；underwater ranging; layered recovery; image recovery; underwater degraded function

国家自然科学基金项目(60772058)资助

2013-12-13;

2014-08-30

王 蕊(1986-)，女，博士生。E-mail:emma_7@163.com

TN911.73

A

1672-5174(2015)09-130-06

10.16441/j.cnki.hdxb.20130448