基于MPI+OpenMP的三维声波方程正演模拟❋
2015-03-15李金山谭惠文
宋 鹏, 解 闯, 李金山❋❋, 谭 军, 刘 伟, 谭惠文
(1. 中国海洋大学海洋地球科学学院,山东 青岛 266100; 2. 中国海洋大学海底科学与探测技术教育部重点实验室,山东 青岛 266100;3. 中国科学院地质与地球物理研究所 中国科学院油气资源研究重点实验室,北京 100029; 4. 中国科学院大学,北京 100049)
基于MPI+OpenMP的三维声波方程正演模拟❋
宋 鹏1,2, 解 闯1, 李金山1,2❋❋, 谭 军1,2, 刘 伟3,4, 谭惠文1
(1. 中国海洋大学海洋地球科学学院,山东 青岛 266100; 2. 中国海洋大学海底科学与探测技术教育部重点实验室,山东 青岛 266100;3. 中国科学院地质与地球物理研究所 中国科学院油气资源研究重点实验室,北京 100029; 4. 中国科学院大学,北京 100049)
针对三维声波方程数值模拟的大计算量和大内存消耗问题,研究并实现了基于MPI+OpenMP的三维声波方程数值模拟并行算法,在PC-Cluster的计算节点间采用基于MPI的按炮分任务的多进程并行模式,在计算节点内采用基于OpenMP的按空间分任务的多线程并行模式,以有效地利用计算和存储资源。3D-Overthrust模型的实验结果显示,基于MPI+OpenMP的三维声波方程数值模拟并行算法的计算效率与基于MPI的按炮分任务并行计算模式相当,但其内存消耗远远低于后者,其更适合于基于大模型或实际模型的三维模拟。
三维声波方程;正演模拟;并行计算;MPI+OpenMP
基于波动方程的地震波正演模拟技术是研究地震波传播规律的有效手段,是地震资料数据处理中诸多处理算法的基础,同时其还可用以指导和优化观测系统设计以及进行地震数据处理结果和地震资料解释的合理性评价,因此深入研究地震波正演模拟技术对于提升整个地震勘探的精度具有重要意义。
目前为止,国内外学者已对基于波动方程的地震波正演模拟技术进行了大量的研究工作[1-8],地震波正演模拟算法已趋于成熟,但三维地震数值模拟由于其数据量大、计算量大和内存消耗高的特点,尚未在工业生产中得到广泛应用。当前,微机群(PC-Cluster)已在地震勘探领域得到普及,而GPU机群也在业界崭露头角,借助于高性能计算集群的并行加速能力来解决三维地震波正演模拟的低计算效率问题已成为业内共识,而合理科学地利用计算资源,深入研究并优化并行算法以显著提高三维地震波正演模拟的计算效率将大力推动其服务于生产的进程。
MPI是当前应用较为广泛的并行编程工具,其具有移植性好、功能强大、使用高效等多种特点[9],国内外学者们针对基于MPI的地震波正演模拟并行算法已开展了诸多卓有成效的研究工作[10-14]。基于MPI的地震波正演模拟并行计算模式有两种,一种是按炮分任务的并行模式,该模式通常根据CPU核数启动相应的进程,每个进程单独执行一炮的计算任务,其避免了进程间的频繁通信,可获得极大的计算加速,但其内存需求较高(计算机内存需大于单炮模拟所需的内存要求);另一种是按空间分任务的并行模式,其将单炮的计算区域划分为多个计算任务并赋予不同的进程执行,降低了内存消耗,但各个进程需频繁通信来交换计算区域边界上的计算结果,降低了并行计算效率。由于大模型或实际模型的单炮模拟内存消耗较高,因此常规的按炮分任务并行模式难以在三维地震波数值模拟当中得到应用,而按空间分任务的并行模式的应用则难以达到令人满意的并行加速比。
OpenMP是实现多线程并行的应用程序编程接口[15]。基于OpenMP的并行计算为线程级并行,其通过简单的高级语言指令即可实现内存共享的多线程并行计算,并且其已为大多数常用的编译器(GCC、ICC、PGI等)所支持,因此目前OpenMP在并行计算领域已逐渐得到广泛地关注。基于OpenMP的各个线程由于内存共享而避免了线程间的频繁通讯,由此可保证其计算效率不会受到并行任务分配模式的影响。
本论文针对基于MPI和OpenMP的并行模式的特点,研究并实现了基于MPI+OpenMP的三维声波方程的交错网格有限差分正演模拟并行算法,其在节点间依然采用基于MPI的按炮分任务多进程并行模式,但其是根据计算节点数(而非CPU核数)启动相应数目的进程,而在节点内采用基于OpenMP的按空间分任务并行模式,根据节点内CPU核数启动相应数目的线程,通过进程和线程的合理配置和管理,既降低三维声波方程数值模拟的内存消耗,又可通过计算资源的高效利用提高三维声波方程数值模拟的计算效率。
1 三维声波方程交错网格有限差分数值模拟
1.1 三维声波方程任意偶数阶精度交错网格差分格式
笛卡尔坐标系下,三维声波方程可表示为一阶应力-速度方程组的形式[4]:
(1)
式中:p为声压;v为波速;ρ为密度;Vx、Vy、Vz分别为x、y、z方向上的质点振动速度,三维空间一阶应力-速度方程组通常应用交错网格有限差分方法求解。
采用交错网格有限差分方法求解(1)式,首先需将(1)式中的各变量进行合理的空间网格剖分(各物理量在交错网格中的空间位置分布如图1所示)。

图1 各变量在交错网格中的空间分布示意图Fig.1 The sketch map of spatial distribution of different variables in the staggered grids
根据各变量的空间分布图,将p的时间一阶微分应用二阶精度差分格式,在整时间点展开,而将p的空间一阶微分按2L(L为正整数)阶差分格式在空间半节点展开,同时将Vx、Vy、Vz在半时间点展开,并将Vx、Vy、Vz的空间一阶微分应用2L阶差分格式在空间整节点展开,最终可得到三维空间一阶速度-压力声波方程组的时间二阶、空间任意偶数阶精度的交错网格差分格式[4]:

(2)
式中:αm为2m(m为正整数且m 1.2 三维声波方程交错网格有限差分模拟的PML边界处理 地震波正演模拟需引入人工边界来界定计算区域,而人工边界若不做特殊处理会产生强边界反射扰乱中心波场。目前对于人工边界的处理方法主要有两种:一种是吸收边界条件方法[16],其在边界上应用近似外行波方程来模拟外行波传播以此达到消除边界反射的目的;另一种是PML(Perfectly Matched Layer)方法[17],其在中心波场计算区域外加上一系列的完全匹配层,层内引入衰减因子,地震波在匹配层之间传播时其能量按传播距离的指数规律衰减以达到衰减边界反射的目的。理论上PML方法对于各个入射角度、各个频率的地震波都有很好的吸收效果,其整体吸收效率要优于常规的吸收边界条件方法,因此本文采用PML方法进行三维声波方程数值模拟的边界处理。 三维声波方程的PML边界处理需在计算区域的各个面(共6个面)上加上一系列的匹配层,各面的匹配层在每个面的边界处发生交叉又会构成12条棱区和8个角点区,因此三维声波方程的正演模拟的PML区域共包含6个面区、12条棱区和8个角点区(PML区域空间分布如图2所示)。 在PML区域内,将p在x、y、z方向上分解为px、py、pz,p=px+py+pz,则各变量在PML区域中按下式计算[4]: (3) (4) 式中:h表示该层与计算区域边界的距离,δ为PML层总厚度,v为波速,R为最外层边界理论反射系数(实际中常取0.0001,但随着PML层的增加,R可以适当减小)。 在PML区域中,面、棱和角点区的衰减系数取值有所不同,在面区,垂直该面方向上的衰减系数不为零,其它两个方向上的衰减系数为零;在棱区,垂直于与该棱相关的两个面方向上的衰减系数不为零,另外一个衰减系数为零;而在角点区域,各个方向上的衰减系数均不为零。 综合以上,三维声波方程交错网格有限差分数值模拟在中心波场区域应用(2)式进行计算,其是一个外层时间,内层三维空间的四层循环,而应用(3)式的边界处理计算同样也是一个四层循环;此外,波场计算时需两个三维数组存放模型的速度和密度,并且由于波场递推计算的需要,每个变量至少还需一个三维数组来存放计算结果,因此三维声波方程交错网格有限差分数值模拟的计算量和内存消耗都相当大。 针对三维声波方程交错网格有限差分数值模拟的计算量和内存消耗大的问题,本文研究并实现了基于MPI+OpenMP的并行计算模式,通过计算节点间进程级并行和节点内线程级并行的有机结合,在有效降低其内存消耗的基础上最大限度地提高三维声波方程数值模拟的计算效率。 2.1 基于MPI的节点间三维声波方程数值模拟并行实现 MPI是一种消息传递并行编程模型标准,其与语言和平台无关,具有实用、可移植性强且灵活高效等诸多优点,是当前应用最为广泛的并行编程环境。 在MPI并行计算中,进程与进程之间的通讯是一个比较耗费时间的过程,如果进程之间的通讯比较频繁,加上交换路由的带宽限制,极易造成网络的阻塞,使得大部分时间耗费在进程间相互通讯的等待上,从而不能发挥并行计算的优势,因此基于MPI的并行计算程序设计的一个原则是尽量减少进程间的通讯。 当前主流的PC-Cluster通常由几十个甚至上千个计算节点组成,每个节点一般包含若干个(一般为2~8个)CPU核,且各核共用该节点的内存。为叙述方便,这里假设模拟应用的PC-Cluster共有N_node个计算节点,每个节点的CPU核数和内存分别为N_core和S,此时理论上采用基于MPI的按炮分任务的并行模式,可同时启动N_node*N_core个进程并通过合理的负载均衡设计而得到理想的并行加速比;但此时每个进程被分配的内存仅为S/N_core,极有可能小于单炮模拟的内存需求,因此本文在计算节点间仅根据节点数启动相应数目的进程,即每个节点上只启动一个进程,这样每个进程可被分配的内存为S,由此可最大限度地保证每个进程所分配的内存足够大。 本文基于MPI的三维声波方程数值模拟的节点间进程级并行计算实现步骤如下: (1)调用MPI_Init,启动并行环境; (2)根据计算节点的数量,调用MPI_Comm_size命令确定进程的个数(一个节点执行一个进程),同时调用MPI_Comm_rank命令获得各进程的标号; (3)各进程分别调用单炮模拟子程序(基于OpenMP实现,详见下节)实现三维声波方程波场模拟; (4)各进程调用MPI_Write,将各进程计算结果并行写入炮集文件; (5)调用MPI_Finalize,结束并行环境。 根据上述步骤实现的三维声波方程数值模拟并行计算,在每个节点上只启动一个进程,也即每个节点上只调用一个CPU核参与计算,因此其可为各个进程提供足够大的内存。当然,该并行模式下每个节点只有一个CPU核参与运算,也造成了计算资源浪费,为充分利用各个节点的计算资源,本文在实现了基于MPI的节点间三维声波方程数值模拟并行计算的基础上,在各个节点内部又根据各个节点的CPU核数,基于OpenMP将每个节点的单进程分解为多个线程,每个CPU核执行一个线程,以充分利用计算资源,提高三维声波方程正演的并行计算效率。 2.2 基于OpenMP的节点内三维声波方程数值模拟并行实现 OpenMP是由OpenMP Architecture Review Board牵头提出的,并已被广泛接受的用于共享内存并行系统的多线程程序设计编译处理方案,其是基于共享内存和线程的支持单指令流多数据流的并行编程模型[19],为编写多线程应用程序提供了简单快捷的途径,而无需程序员进行复杂的线程创建、同步、销毁等工作,使得线程级并行的实现变得更加简单易行。 基于OpenMP的各线程内存共享,因此对于三维声波方程数值模拟来讲,可以应用OpenMP将单炮的计算任务进行线程级任务划分,并不需进行频繁的网络通信,由此可保证其计算效率不会受到网络堵塞的影响。 OpenMP通常采用引语的方式,对程序的循环部分进行并行化,但要求用于并行的循环部分其每次循环互不相关。三维声波方程数值模拟的计算任务为一个四层循环(最外层是时间,内层依次为x、y、z方向上的空间循环),由于每个时间切片上的当前循环均依赖于上一个时间切片上的计算结果,即时间循环中各个时间切片存在相关性,因此对于时间循环来讲其并不适合于基于OpenMP的并行,但对于内层的x、y或z方向上的空间循环,其任两次循环之间均不存在相关性,具备应用OpenMP进行并行计算的条件,因此每一层空间循环都可被指定进行并行计算(本文选择将x方向的循环指定为并行运算区域)。此外,基于OpenMP的并行计算其每次线程的启动也会需要一定的时间开销,因此并行计算当中也要尽量避免线程的频繁启动和销毁操作,因此本文将三维声波方程数值模拟的线程启动置于时间循环层外,在整个单炮模拟过程中仅需进行一次线程的启动和销毁。 本文基于OpenMP的节点内三维声波方程数值模拟线程级并行计算实现步骤如下: (1)根据当前节点的CPU核数,调用int_omp_set_num_threads函数设置当前节点所启动线程的数目(即一个CPU核执行一个线程); (2)在时间循环层外部调用#pragma omp parallel num_threads语句,将三维声波方程数值模拟的四层循环设定为并行计算区域; (3)在时间循环层外部调用omp_get thread_num函数,得到当前的线程号,然后通过任务划分得到各线程在x方向上对应的起止网格点号; (4)将各线程在x方向上的起止网格点号代入x方向的循环语句中,即可实现沿x方向分任务的多线程并行计算。 本文基于3D-Overthrust模型进行三维声波方程的数值模拟并行计算效率和内存消耗测试。3D-Overthrust模型是SEG/EAEG设计的一个三维地质模型,是当前测试三维数值模拟、成像及反演精度的标准模型。该模型长、宽均为10km,深度为2.325km,空间采样步长为12.5m,其描述了一个推覆地层在早期形成的扩展断裂序列上的不整合覆盖,并且其上覆层顶部为一个复杂的风化带(3D-Overthrust速度模型如图3所示,过模型中心垂直于x方向和垂直于y方向的速度切片如图4所示)。 图3 3D-Overthrust速度模型Fig.3 3D-Overthrust velocity model 本文应用一个包含59个节点,每个节点4G内存且包含4个核(CPU型号为AMD2.4)的PC-Cluster,分别基于MPI的按炮分任务并行模式(以下简称基于MPI)和基于MPI+OpenMP的并行算法(以下简称基于MPI+OpenMP)对3D-Overthrust模型进行一个航次共236炮的数值模拟。模拟的震源采用主频为30Hz的雷克子波,时间采样间隔为0.5ms,模拟时间长度为1.6s。密度采用1500kg/m3的常密度模型,速度模型和密度模型的空间采样步长均为12.5m。观测系统为单边放炮8线接收,每线160道,炮间隔、线间隔、道间隔均为25m,检波点深度为12.5m。炮点位于第四线和第五线中间,最小偏移距为100m,起始炮点位置位于(4075m,325m,12.5m),X方向和Y方向的模拟孔径均为500m,每炮模拟最大覆盖区域的空间范围为4075m×1175m×2325m(观测系统示意如图5所示,基于该观测系统数值模拟所得第160炮单炮记录如图6所示)。 ((a)为垂直于x方向的速度切片。(a) is the velocity slice perpendicular to thexdirection;(b)为垂直于y方向的速度切片。(b) is the velocity slice perpendicular to theydirection.) 图4 过模型中心的速度切片 本文分别基于MPI和基于MPI+OpenMP,对于3D-Overthrust模型的三维声波方程正演模拟的计算时间和内存消耗见表1。 图5 观测系统示意图Fig.5 The sketch map of the acquisition geometry 图6 第160炮单炮记录Fig.6 The seismic record of the 160th shot 并行模式Parallelpattern236炮的计算时间/sThecalculatingtimeof236shots每个节点的内存消耗/MThememoryconsnmptionofeachnode基于MPI96121253基于MPI+OpenMP9735315 由表1可知,基于MPI+OpenMP的三维声波方程数值模拟其计算效率与基于MPI的按炮分任务并行模式基本相当,但其内存消耗却仅约为基于MPI的按炮分任务并行模式的1/4,因此理论上其更适合于大模型或实际数据的三维声波方程数值模拟。 本文研究并实现了基于MPI+OpenMP并行计算模式的三维声波方程的交错网格有限差分数值模拟并行算法,在节点间采用基于MPI的按炮分任务多进程并行模式,在节点内采用基于OpenMP的按空间分任务并行模式,实现了计算和存储资源的高效利用。3D-Overthrust实验结果显示,基于MPI+OpenMP的三维声波方程数值模拟其计算效率与基于MPI的按炮分任务并行模式相当,但其内存消耗却大大低于基于MPI的按炮分任务并行模式,因此基于MPI+OpenMP的并行算法更适合于大模型或实际模型的三维声波方程数值模拟,有望推动三维地震波数值模拟进入大规模生产领域。 此外,基于MPI+OpenMP的并行算法同样适应于三维弹性波模拟、三维逆时偏移以及三维全波反演等大计算量和大内存消耗地球物理问题的并行计算,也同样适应于基于GPU机群的海量数据并行计算。 [1] Virieux J. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11): 1933-1942. [2] Virieux J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901. [3] 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. [4] 牟永光, 裴正林. 三维复杂介质地震数值模拟[M]. 北京: 石油工业出版社, 2005. [5] 井涌泉, 高红伟, 王维红. 二维各向同性介质 P 波和 S 波分离方法研究[J]. 地球物理学进展, 2008, 23(5): 1412-1416. [6] 张会星, 何兵寿, 张晶, 等. 复杂各向异性介质中的地震波场有限差分模拟[J]. 煤炭学报, 2008, 33(11): 1257-1262. [7] 孙银行. 弱各向异性介质弹性波的准各向同性近似正演模拟[J]. 地球物理学进展, 2008, 23(4): 1118-1123. [8] 宋鹏, 王修田. 优化系数的四阶吸收边界条件[J]. 中国海洋大学学报 (自然科学版), 2008, 38(2): 251-258. [9] 都志辉. 高性能计算之并行编程技术—MPI 并行程序设计[M]. 北京: 清华大学出版社, 2001: 13-15. [10] 王德利, 雍运动, 韩立国, 等. 三维粘弹介质地震波场有限差分并行模拟[J]. 西北地震学报, 2007, 29(1): 30-34. [11] 王月英. 基于MPI的三维波动方程有限元法并行正演模拟[J]. 石油物探, 2009, 48(3): 221-225. [12] 何兵寿, 张会星, 韩令贺. 弹性波方程正演的粗粒度并行算法[J]. 地球物理学进展, 2010(2): 650-656. [13] 秦艳芳, 王彦宾. 地震波传播的三维伪谱和高阶有限差分混合方法并行模拟[J]. 地震学报, 2012, 34(2): 147-156. [14] 张明财, 熊章强, 张大洲. 基于MPI的三维瑞雷面波有限差分并行模拟[J]. 石油物探, 2013, 52(4): 354-362. [15] Chandra R, Menon R, Dagum L, ed. Parallel programming in OpenMP[M]. [s.l.]: Morgan Kaufmann, 2001. [16] Enquist B, Madja A. Absorbing boundary conditions for the numerical simulation of wave[J]. Math Comp, 1977, 31: 629-651. [17] Bérenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Comp Physics, 1998, 114(1): 185-200. [18] Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66: 294-307. [19] 王恩东, 张清, 沈铂, 等. MIC高性能计算编程指南[M]. 北京: 中国水利水电出版社, 2012. 责任编辑 徐 环 The 3D Modeling of Acoustic Wave Equation Based on MPI+OpenMP SONG Peng1,2, XIE Chuang1, LI Jin-Shan1,2, TAN Jun1,2, LIU Wei3,4, TAN Hui-Wen1 (1. College of Marine Geo-Science, Ocean University of China, Qingdao 266100, China; 2. Key Lab of Submarine Geosciences and Prospecting Techniques,Ministry of Education, Qingdao 266100, China; 3. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Beijing 100029, China; 4. University of Chinese Academy of Sciences, Beijing 100049, China) For the problem of large computational amount and memory consumption of the 3D modeling based on acoustic wave equation, a parallel algorithm based on MPI+OpenMP is studied and implemented in the paper. The algorithm applies the multi-process parallel pattern of task allocation by shots based on MPI among the computing nodes of a PC-Cluster, and uses the multi-thread parallel pattern of task allocation by spaces based on OpenMP within the nodes, so the computational and storage resources can be utilized more effectively. The test of the 3D-Overthrust model shows that the 3D modeling of acoustic wave equation based on MPI+OpenMP has nearly the same computing efficiency as that only based on MPI, but far less memory is needed. Therefore, the parallel algorithm based on MPI+OpenMP is more suitable than that based on MPI for the 3D acoustic wave equation modeling of huge models or real models. 3D acoustic wave equation; forward modeling; parallel computing; MPI+OpenMP 中央高校基本科研业务费专项(201513005);国家大学生创新训练项目(201410423033)资助 2015-01-13; 2015-03-06 宋 鹏(1979-),男,讲师,主要从事全波形反演及计算机高性能运算研究。E-mail:pengs@ouc.edu.cn ❋❋ 通讯作者: E-mail:ljs@ouc.edu.cn P631.4 A 1672-5174(2015)09-097-07 10.16441/j.cnki.hdxb.201500082 基于MPI+OpenMP的三维声波方程数值模拟并行计算
3 基于MPI+OpenMP的三维声波方程数值模拟效果分析
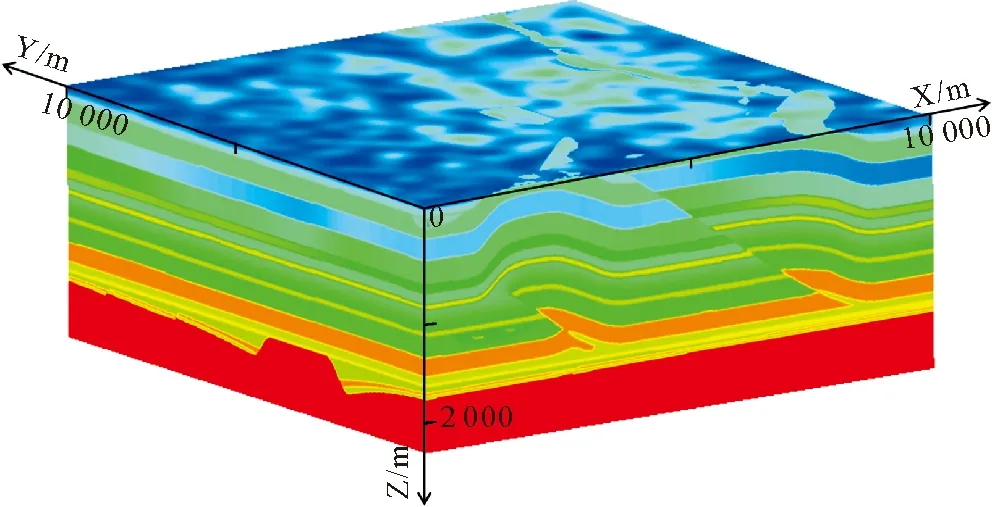
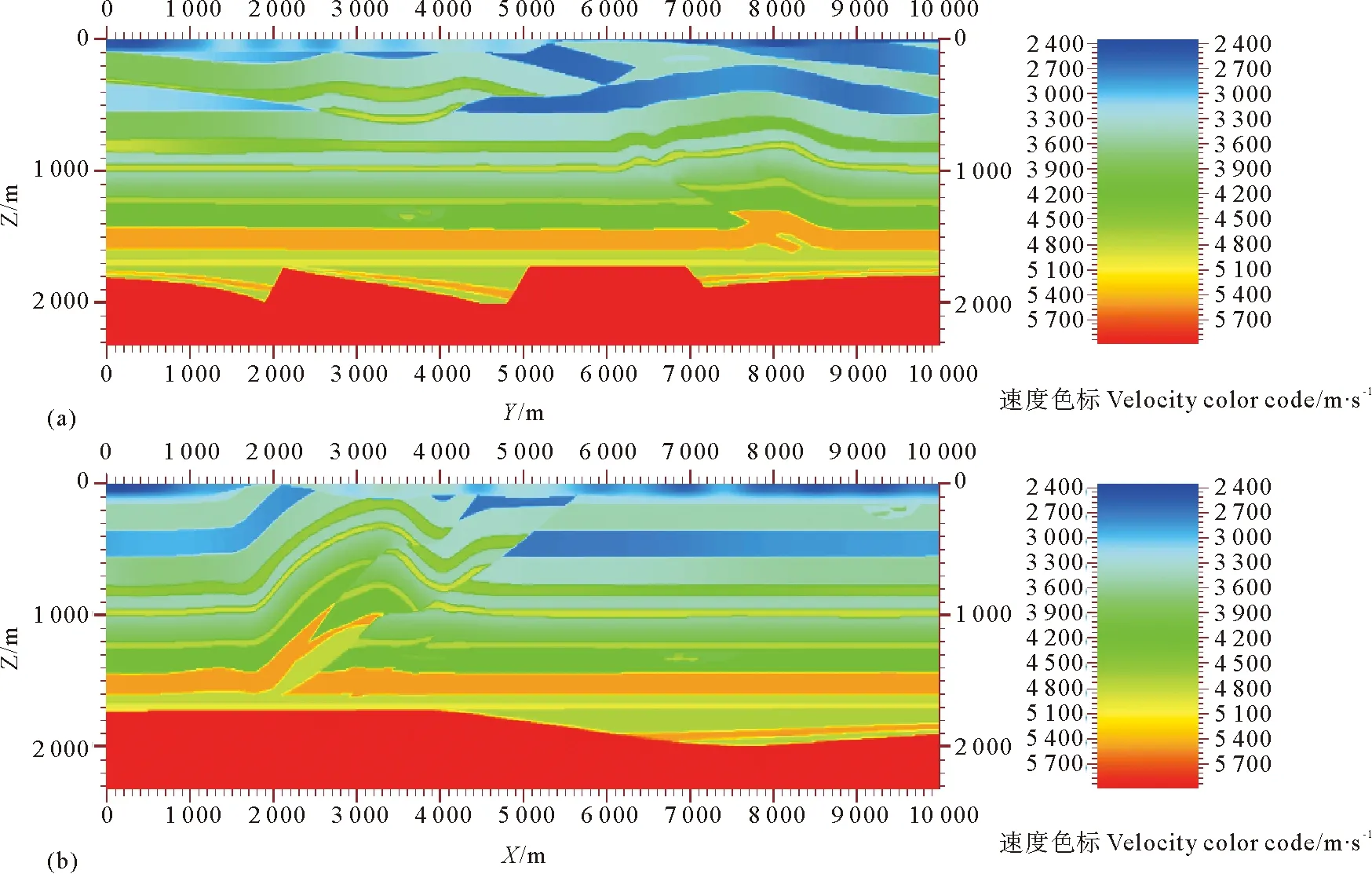
Fig.4 The velocity slices that cross the center of model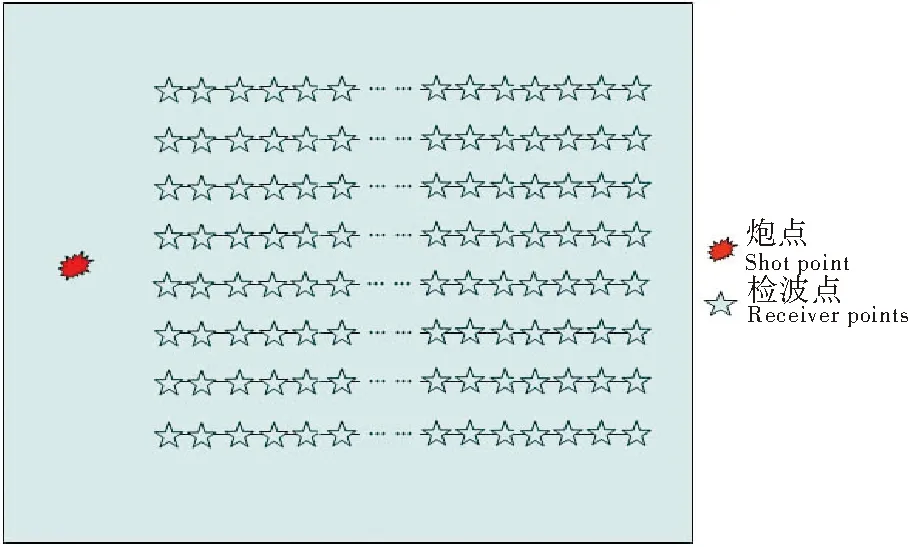
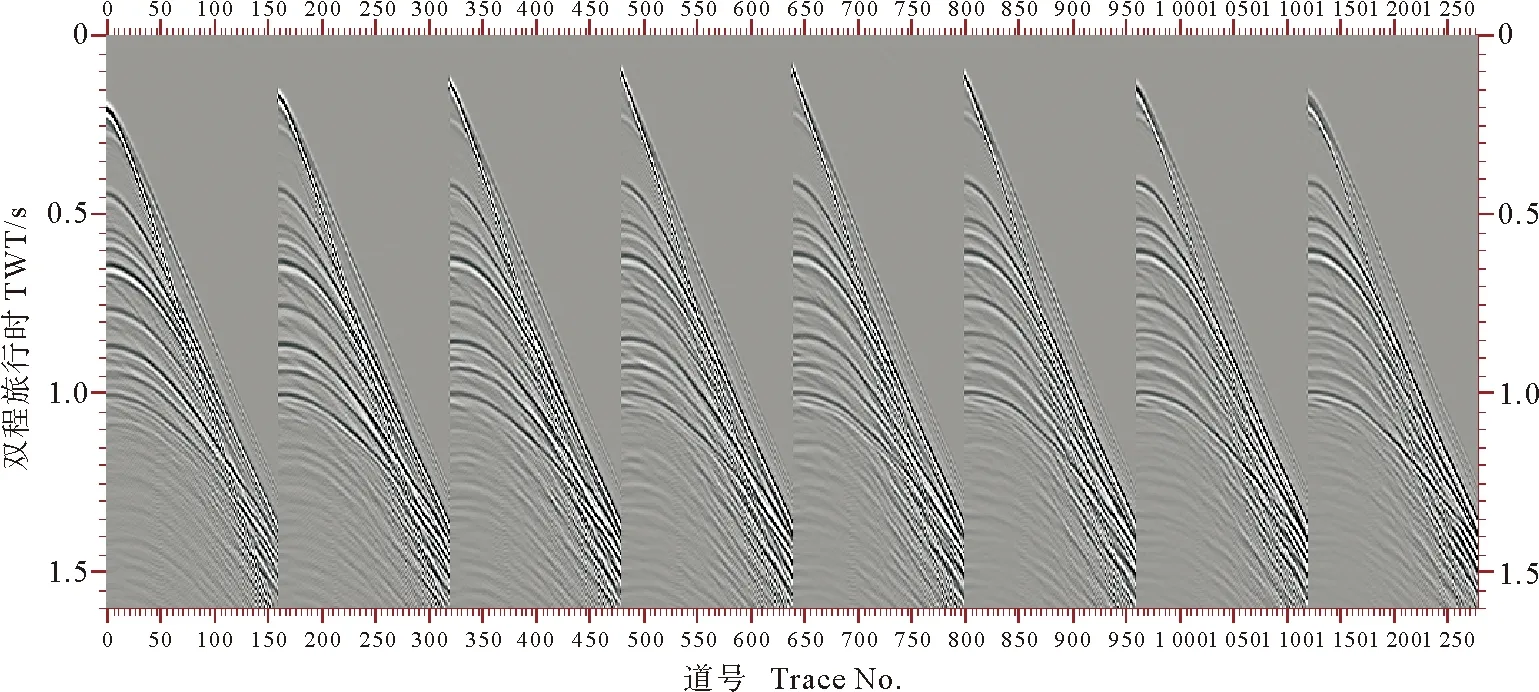

4 结论与展望
