舵系统加速寿命试验方案优化设计*

柳爱利 寇昆湖

(海军航空工程学院控制工程系 烟台 264001)



舵系统加速寿命试验方案优化设计*

柳爱利 寇昆湖

(海军航空工程学院控制工程系 烟台 264001)

论文对导弹舵系统的加速寿命试验方案进行了优化设计。优化设计过程以舵系统在贮存应力水平下,p阶分位寿命渐近方差最小作为优化设计的准则,以舵系统中位寿命渐近方差作为舵系统加速寿命试验方案优化目标函数。通过寻优计算,得到了导弹舵系统在温度和湿度两个试验应力作用,应力水平组合数为4和5时,其温度和湿度的应力水平、样本分配比例νi、每组试验截尾时间τi的最优值,并利用方差因子相对百分比确定了此时的合理测试次数为6。对优化方案进行的敏感性分析表明,优化试验方案对导弹舵系统的加速模型参数具有较好的鲁棒性。

导弹舵系统; 加速寿命试验; 优化设计; 鲁棒性

Class Number E927

1 引言

导弹舵系统是一种高可靠性产品,如果采用现场贮存试验来评估其可靠性,试验数据的获取是一个漫长的过程,不便于可靠性评估。因此,有必要对舵系统进行加速寿命试验,保证在失效机理不变的前提下,通过其加速模型,利用高应力水平下的寿命特征取评估舵系统在正常应力水平下的寿命特征。以便在较短时间内,获得其失效数据,继而对其进行可靠性评估。加速寿命试验的目的是利用试验数据来预测产品的可靠性,因此试验方案的合理性直接影响试验数据的质量和产品可靠性的预测结果,决定了评估结果的真实可信程度。

而对舵系统加速寿命试验方案进行优化设计,可有效提高试验效率和舵系统在贮存应力下寿命指标估计值的精确度。优化试验方案是在一定约束条件下,目标函数取得最小值所对应的一组方案。目前,神经网络、遗传算法、模拟退火等优化方法,对于复杂的优化过程有很好的效果[1]。根据在舵系统加速寿命试验中应力水平的具体特点,论文采用迭代的方法来搜索目标函数的最优值。

2 舵系统加速试验方案的优化设计

2.1 加速试验方案相关参数的确定

舵系统加速试验以温度和湿度作为加速应力。在对舵系统加速寿命试验方案优化设计之前,先确定相关参数。

1) 温度应力水平

温度应力的取值范围在正常贮存温度和最高承受温度之间,即T∈(20,60),相应的温度应力水平为

相应的温度应力转换水平范围为x∈(3.002×10-3,3.411×10-3)。

2) 湿度应力水平

湿度应力的取值范围在正常贮存湿度和最高承受湿度之间,即H∈(50%,95%),相应的湿度应力水平为

相应的温度应力转换水平范围为y∈(-0.0513,-0.6931)。

3) 各组试验截尾时间

根据前期工程经验及舵系统加速试验的可行性,取加速试验截尾时间上限τU=150天。

4) 优化模型参数初始值

在进行优化设计之前,给定模型参数先验值,作为优化设计模型参数的初始值[1]。舵系统以温度和湿度为加速应力的加速模型为

lnθ=β0+β1x+β2y

(1)

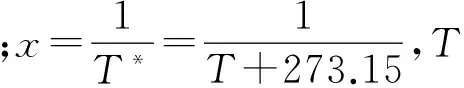
加速模型参数的先验值β*=[-26.6,9878.0324,-0.9]。

2.2 舵系统加速试验优化准则

方案以舵系统贮存应力水平下,p阶分位寿命渐近方差最小为准则,对舵系统加速寿命试验方案进行优化设计。

根据式(2)舵系统的加速模型为指数分布,寿命分布参数μ的表达式为

μ=lnθ=β0+β1x+β2y

(2)

由极值分布的性质,舵系统在正常贮存应力水平下的p阶分位寿命为[3]

ϑp(x0,y0)=μ(x0,y0)+γp=β0+β1x0+β2y0+γp

(3)

其中,γp为标准极值分布的p阶分位数。当p=0.5时,γ0.5=-0.3665,此时ϑp(x0,y0)即为舵系统的中位寿命。

2.3 舵系统加速寿命试验方案优化的目标函数

舵系统优化目标函数为

Ψ=AVar[ϑp(x0,y0)]

(4)

其中,AVar[ϑp(x0,y0)]为正常贮存应力水平下舵系统的p阶分位寿命渐近方差。

由δ方法[1]可得:

AVar[ϑp(x0,y0)]=ETVE

(5)

其中,

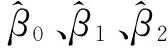
(6)

参数估计值的方差协方差矩阵V是Fisher信息矩阵F的逆矩阵[5],即V=F-1。Fisher信息矩阵是对数似然函数负二阶偏导数矩阵的数学期望[5],即

(7)

其中,L为舵系统加速寿命试验的对数似然函数。

假设舵系统加速寿命试验的样本量为n,每组试验下的样本量为nνi,νi为每组试验中样本比例。这里直接给出Fisher信息矩阵如下

(8)

因此,舵系统加速寿命试验方案优化目标函数可表示为

AVar[ϑp(x0,y0)]=ETF-1E

(9)

式中,NU为应力水平组合数为U时的方差因子。

由式(9)知,在n确定的情况下,舵系统的p阶分位寿命渐近方差取决于NU。而NU是一个只与样本分配比例νi、温度和湿度应力水平xi、yi、每组试验截尾时间τi有关的函数。因此,在舵系统加速寿命试验优化方案中需要进行优化的变量为样本分配比例νi、温度和湿度应力水平xi、yi、每组试验截尾时间τi。若用Ω来表示优化变量,则

Ω=(νi,xi,yi,τi) (i=1,2,…,U)

温度和湿度的正常工作应力水平T0和H0、最高应力水平TU和HU、截尾时间τU在2.1节已确定。NU的大小只取决于温度应力T1,T2,…,TU-1和湿度应力H1,H2,…,HU-1及样本分配比例νi和每组试验的截尾时间τi。

对试验应力采用等间隔设计[7],即

(10)

其中,xi=1/Ti+273.15,yi=lnHi。

根据式(10)可知,只要知道x1、xU和y1、yU就可以得到中间的各个应力水平。TU和HU已经给定,只需确定x1和y1即可。所以,简化后的优化变量表示为

Ω′=(νi,x1,y1,τi) (i=1,2,…,U)

综上可以得出舵系统加速寿命试验方案优化设计的数学模型,其表达式为

(11)

2.4 方案的优化设计结果

导弹舵系统加速寿命试验方案最优搜索的具体过程如图1所示,以U=4、U=5为例,优化结果如表1、表2所示。

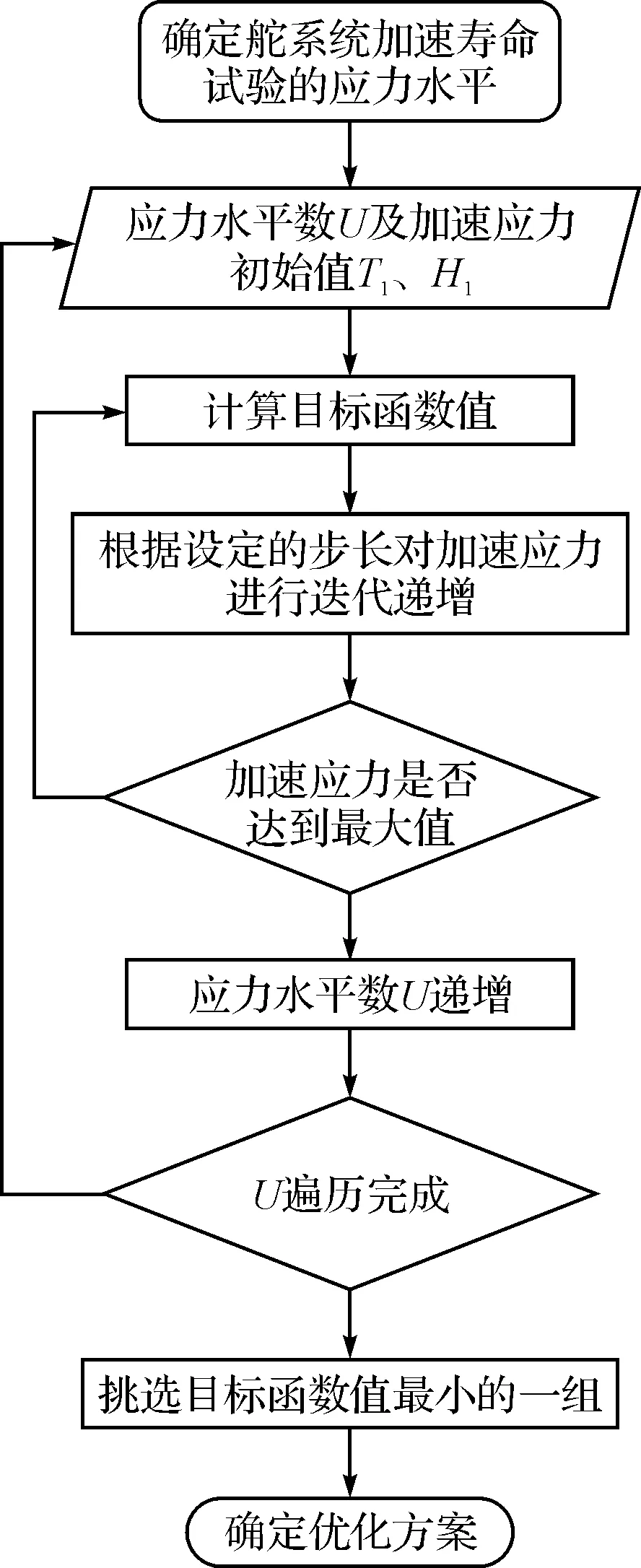
图1 加速试验方案的优化设计流程

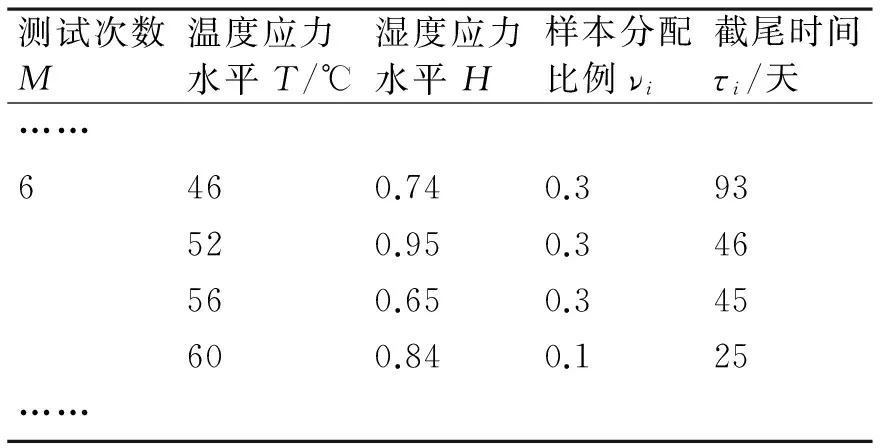
测试次数M温度应力水平T/℃湿度应力水平H样本分配比例νi截尾时间τi/天……6460.740.393520.950.346560.650.345600.840.125……

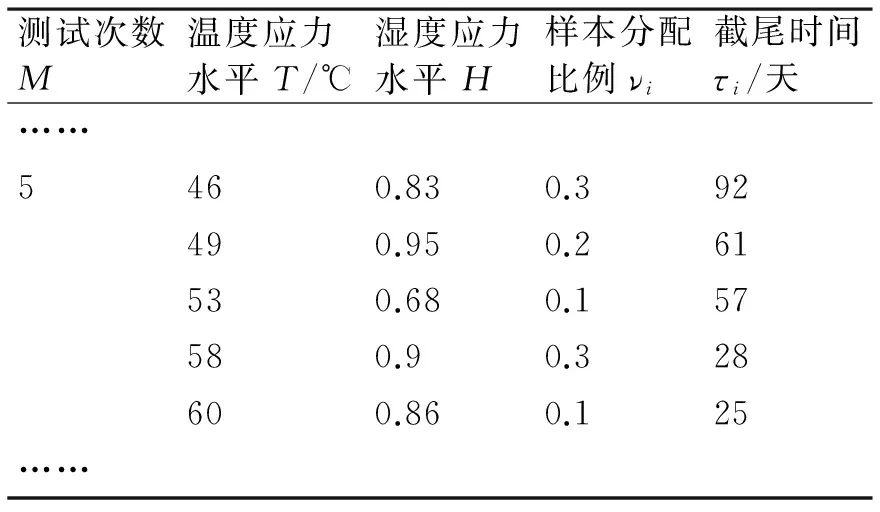
表2 U=5时舵系统加速寿命试验方案优化设计结果

在舵系统加速试验过程中,测试次数需要合理选择。论文利用方差因子相对百分比[8]来确定测试次数,然后利用等对数间隔来确定测试时间。

方差因子百分比Rj,j+1的表达式为

(12)

其中,NU,j为观测次数为j时的方差因子。

对于加速应力水平组合数为U=4、5时,方差因子相对比与观测次数j之间的关系如图2所示。

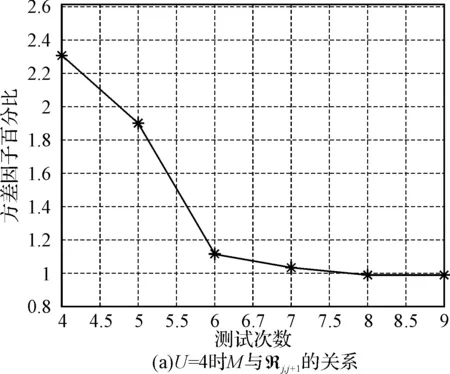
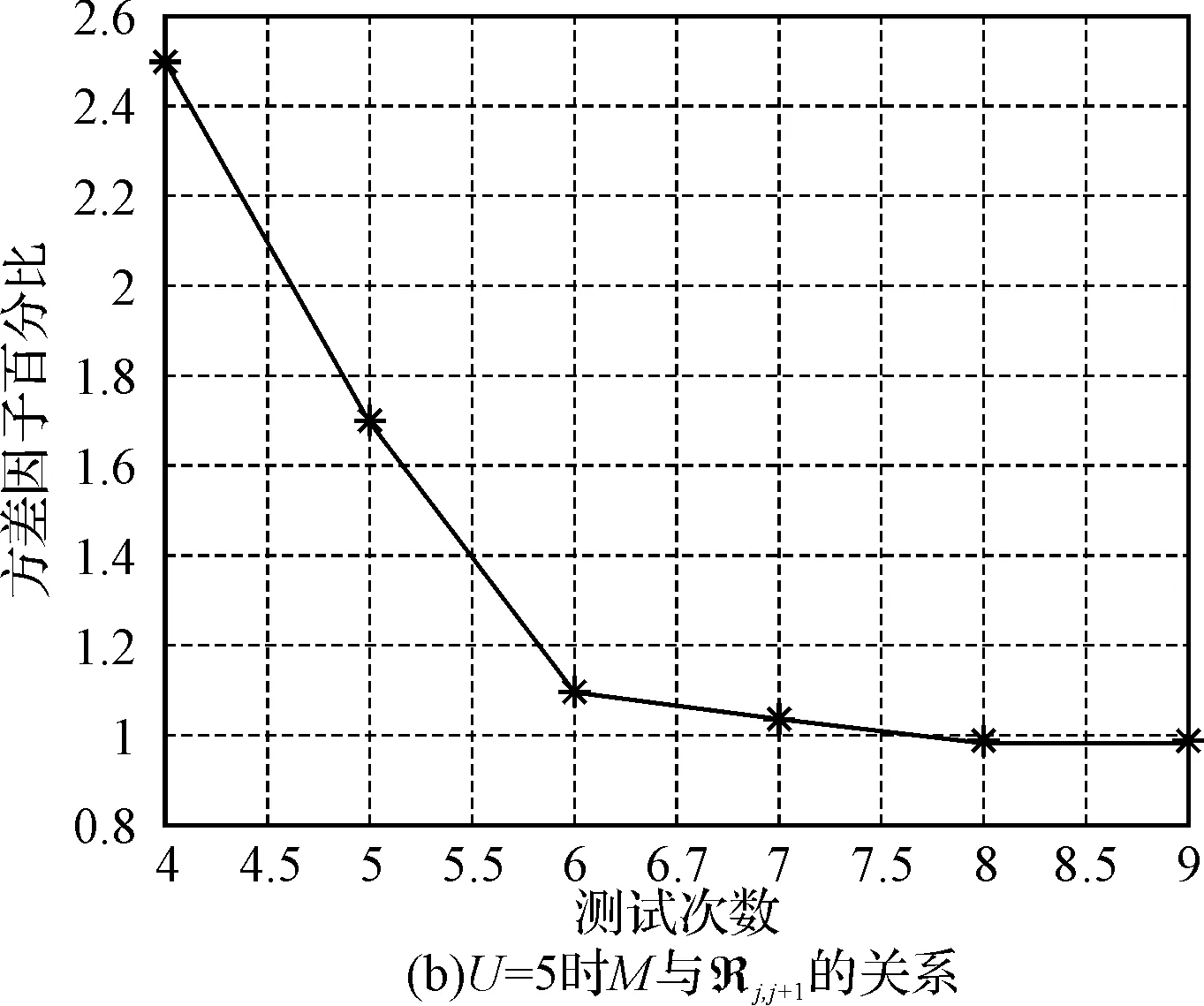
图2 测试次数M与方差因子百分比Rj,j+1关系图

从图中可以看出,当测试次数M≥6时,方差因子百分比Rj,j+1基本稳定下来,也就是说当测试次数M≥6,观测次数的变化对方差因子的影响已经很小。

舵系统样本量为12时,最终确定舵系统的加速寿命试验方案如表3所示。

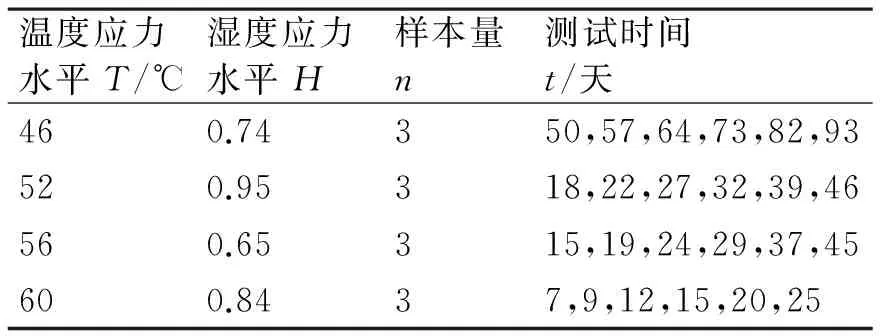
表3 舵系统加速寿命试验方案

3 舵系统加速寿命试验优化方案敏感性分析

下面通过比较来分析模型参数对舵系统加速试验优化方案的敏感性[10]。模型偏差取值为±1%时,舵系统加速寿命试验优化方案敏感性分析结果如表4所示。从表中可以看出,当模型参数β0、β1、β2发生变化时,样本分配比例νi、截尾时间τi与最优方案相比都有一定的变化,但方案仍具有较好的鲁棒性。考虑到试验方案对参数β0的敏感性,在实际应用中应精确给出其初始估计值,以提高方案的设计及可靠性分析的精度。

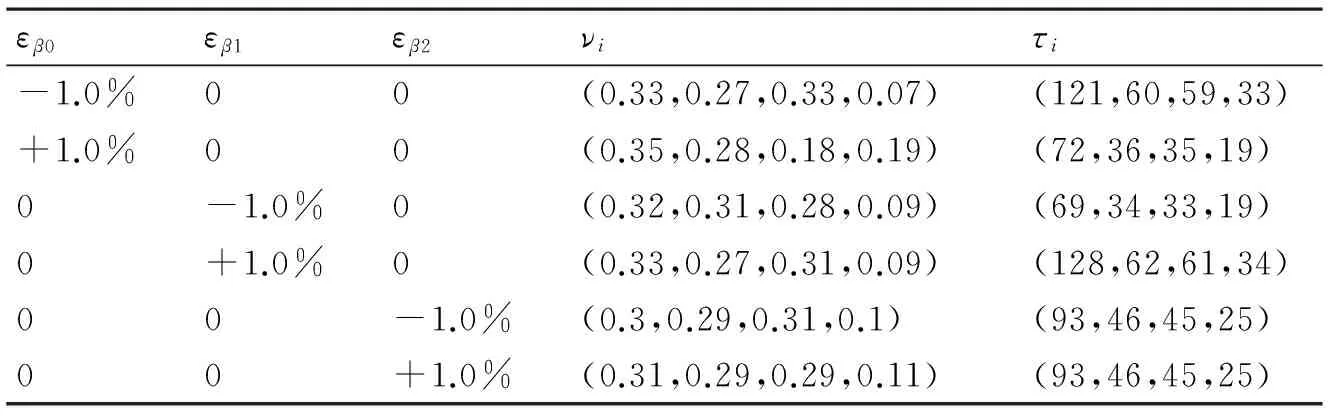
表4 模型偏差±1%优化方案的敏感性分析结果

4 结语

论文在舵系统加速试验方案基础上对方案进行了优化设计。通过引入均匀正交试验方法,确定了加速应力的组合方式;以舵系统中位寿命渐近方差为目标函数,以极大似然估计理论为基础,对加速应力水平及测试时间等变量进行了优化,确定了舵系统的加速寿命试验方案,即选择舵系统样本量为12,每组样本量取3,并确定了每组应力水平下的等间隔测试时间。优化方案的敏感性分析表明,优化方案对参数具有较好的鲁棒性。

[1] 游达章.数控系统加速寿命试验方法及可靠性评估技术研究[D].武汉:华中科技大学,2011.

[2] 谭源源.装备贮存寿命整机加速试验技术研究[D].长沙:国防科学技术大学,2010.

[3] 曹晋华.可靠性数学引论[M].北京:高等教育出版社,2006.

[4] 吴翊,李永乐,胡庆军.应用数理统计[M].长沙:国防科技大学出版社,2008.

[5] 钱萍.航天电连接器综合应力加速寿命试验与统计分析的研究[D].杭州:浙江大学,2010.

[6] 戴树森.可靠性试验及其统计分析[M].北京:国防工业出版社,1983.

[7] 茆诗松,王玲玲.加速寿命试验[M].北京:科学出版社,1997.

[8] Ahmad A T, Bhaskara R M, Zhang H M. Periodic inspection plans: the case of Weibull distribution[J]. Metrica,2003,58(8):15-30.

[9] 冯红艺.航天电连接器综合应力加速寿命试验优化设计与统计分析的研究[D].杭州:浙江大学,2006.

[10] Yu H F, Tseng S T. Designing a degradation experiment[J]. Naval Research Logistics,1999,46(4):689-706.

Design of Accelerated Life Test Optimized Plan for Missile Rudder System

LIU Aili KOU Kunhu

(Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001)

The accelerated life test plan of a missile rudder system is optimized in this paper. According to this optimization method, the design criterion is to minimize thePorder division asymptotic variance of the rudder’s life, so the optimization objective function is asymptotic variance. Through optimization calculation, the optimal values of stress levels, the proportionνiof every group’s distribution, the test time quantumτiof every group are worked out while different stresses of temperature and humidity are divided in 4 or 5 levels. The reasonable test number is 6 times comparing the variance factor relative percentage. Sensitivity analysis of the optimized plan shows that the plan has good robust to the parameters of the accelerated model.

missile rudder system, accelerated life test, optimization design, robustness of optimized ALT plan

2014年10月8日,

2014年11月21日

柳爱利,女,博士,教授,研究方向:导航、制导与控制。寇昆湖,男,博士,讲师,研究方向:导航、制导与控制。

E927

10.3969/j.issn1672-9730.2015.04.030