基于改进粒子群算法的HMM训练研究与应用

张 璐 芮 挺 朱会杰 周 游

（1.解放军理工大学国防工程学院，江苏 南京210007；2.江苏经贸职业技术学院，江苏 南京210007）

0 引言

滚动轴承是旋转机械的关键部件，其直接影响整个机械系统的性能和效率，也是引起旋转机械故障的主要原因之一［1］。据统计，大约有30%的旋转机械故障是由滚动轴承故障引发，因此研究滚动轴承的故障诊断对于保证旋转机械正常运转有重要意义。

隐马尔可夫模型（Hidden Markov Model，HMM）是一种概率统计模型，在语音识别、状态监测、故障诊断、生物信号处理等信号处理和模式识别领域得到广泛应用［2］。HMM的应用建立在训练的基础上，然而经典的Baum－Welch训练算法是一种基于最陡梯度下降的局部优化算法，该算法的缺点是对初始值的选取依赖大，且容易陷入局部最优解。

因此本文针对HMM原有训练算法存在的问题，提出一种基于极值扰动和自适应惯性权重的粒子群算法的模型训练算法，采用全局搜索策略优化模型参数，提高模型在故障诊断中的准确性。

1 隐马尔可夫模型

隐马尔可夫模型包含了双内嵌式的随机过程：一个是马尔可夫链，它负责描述随机过程状态的转移；另一个是隐马尔可夫链中状态相关的观测序列，它负责描述状态和观察值之间的统计对应关系。在HMM中观察到的事件与状态并不是一一对应的，而是通过一个随机过程去感知状态的存在及其特性。由于不能直接看到状态，因而称为隐马尔可夫模型［3］。

2 粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）是一种基于迭代的群体优化方法。所有粒子都具有相应的速度V（t）和位置X（t），每个粒子根据它的位置都会产生一个适应度值。将每个粒子视为问题的一个可行解，通过一组随机解对系统进行初始化后，迭代搜寻得出最优值［4］。在迭代过程中，每个粒子通过跟踪两个极值不断调整运动速度和位置：一个极值是粒子本身目前找到的最优解，即个体历史最优值pbest；另一个极值是整个种群目前找到的最优解，称为全局最优值gbest，从而实现在搜索空间的寻优。其公式表示为：

式中，ω为惯性权重；c1、c2为学习因子；r1、r2为［0，1］区间内均匀分布的伪随机数。

3 改进的粒子群算法

3.1 极值扰动

本文提出扰动策略的算法，使种群始终处于一种非平衡态，促使粒子在精英学习机制的基础上扩大探测范围，增加群体多样性，从而提高算法的搜索能力。扰动算子如下：

式中，rand为［0，1］区间内的均匀分布。

采用扰动策略改进粒子群算法，主要是通过对种群最优值添加持续的小范围扰动。每相隔十代，比较两个全局最优值，若差值小于一定阈值，说明粒子群有陷入局部最优、濒临停滞的可能性，给全局最优值加上扰动，通过粒子群的学习机制，可将整体带出局部最优。比较两代全局最优值设定固定步长的目的是减少运算量，提高算法效率。表达式为：

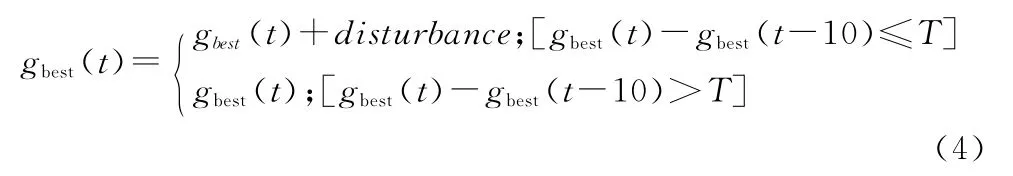
3.2 惯性权重的设计

惯性权重使粒子保持运动惯性，同时扩展搜索空间。较大的惯性权重有利于全局探索，而较小的惯性权重有利于算法的局部开发，加速算法的收敛。在全局搜索算法中，希望前期有较高的搜索能力以得到合适粒子，而后期有较高的开发能力，以加快收敛速度［5］。为平衡算法的全局搜索能力和收敛速度，本文采用基于高斯函数递减惯性权重的调整策略，即：

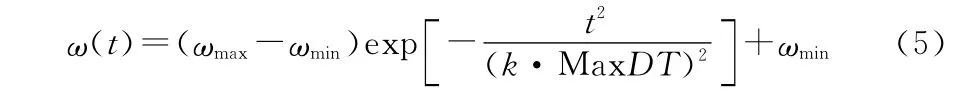
式中，MaxDT为粒子群算法中的最大循环次数；t为当前迭代次数；k为一个常数值，较小的k值会使ω（t）迅速减小，较大的k值会使ω（t）变化减慢。

当选定k值后，ω（t）随着迭代次数的增加而减小，加快了算法的收敛速度。在算法程序中设置一个小的固定值D作为精度值，在程序运行过程中，当ω－ωmin＞D时，按照式（5）更新惯性权重；反之，当ω－ωmin≤D时，ω＝ωmin。

4 基于粒子群优化算法训练HMM

针对HMM训练算法存在的问题，本文采用粒子群优化算法训练HMM，具备了全局搜索、快速收敛的能力，能够降低初始值的影响，提高模型的训练算法逼近函数极值的能力。

4.1 HMM解的编码

设状态转移矩阵A、观察值输出矩阵B、初始状态分布矩阵π为粒子位移表达式X（t）＝［π，A，B］。将粒子群算法最终获得的全局最优解作为HMM中的各个参数。由于各元素的取值范围要在［0，1］之间以及各行元素要满足和等于1的条件，所以首先分别对π、A、B进行归一化处理。进而，HMM的参数训练过程就转变为求取适应度函数最大值的问题。

4.2 适应度函数

在训练过程中，选取产生观测序列O的概率P（O｜λ）作为适应度函数，具体函数为f（λ）＝P（O｜λ）。考虑到HMM模型的概率值P（O｜λ）相对较小，且只关心每次模型输出概率值的相对大小，现将上述函数两边取对数作为本算法中的适应度函数。

4.3 算法流程

（1）给定初始化条件，设置学习因子、惯性权重、粒子群规模、最大速度、最大迭代次数等参数，同时设定HMM的状态数、观测值数以及观测序列；（2）对π、A、B矩阵归一化，按照式（1）、（2）更新速度、位移；（3）按照式（5）更新惯性权重，计算适应度函数，更新个体最优值、全局最优值；（4）判断是否加入扰动算子，若达到终止条件，输出最优解和对应适应值，否则转向（3）。

5 实验与分析

实验样本来源于安装在电机驱动端的6205－2RS深沟球滚动轴承的振动加速度数据。具体实验设置如表1所示（每组样本釆样点为1 024个）。

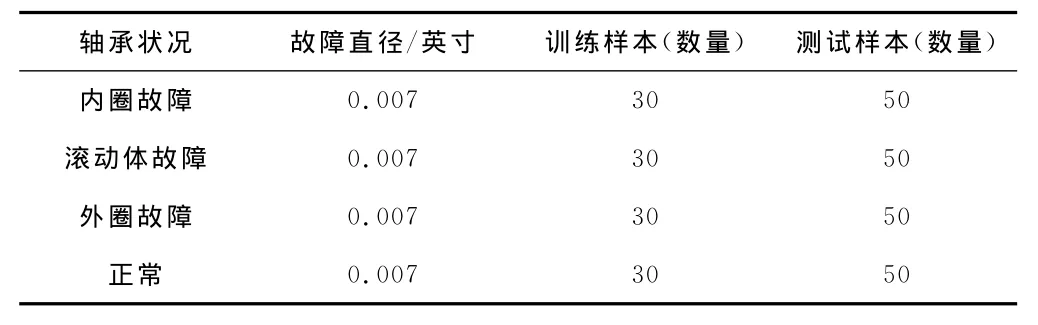
表1 实验数据的设置

5.1 HMM的训练

在训练阶段，采用本文提出的粒子群优化算法训练左右型的HMM。将经过三层小波包分解、特征提取、特征降维等信号处理后的多维观测矩阵作为HMM的训练集。设定隐状态的数目为4。每种故障状态下选取30个样本进行训练。粒子群算法参数设置为：粒子群个体数目Num＝100，c1＝c2＝1.496 2，ωmin＝0.4，ωmax＝0.9，最大迭代次数为500次。初始状态分布矩阵π的初值为［1，0，0，0］，A、B矩阵的初始值为归一化的随机值。

训练结束后，将得到内圈故障、滚动体故障、外圈故障和正常状态对应的4个模型，分别为HMM－1～HMM－4。图1为训练后的4种故障类型对应HMM的对数似然率。

5.2 实验结果

测试阶段，对每种故障状态下的各50个样本振动信号进行同样的信号处理和特征提取过程，然后分别输入训练后的4组模型中，将获得最大适应度函数值P（O｜λ）的模型识别为当前的轴承状态。表2为HMM诊断的具体统计结果。

由表2可以看出HMM具有较好的分类性能，对4种轴承故障的识别率均在92%以上。HMM的训练和诊断实验结果表明HMM轴承故障诊断方法算法稳定、训练速度快、分类准确率高，可以用于轴承的故障诊断工作。

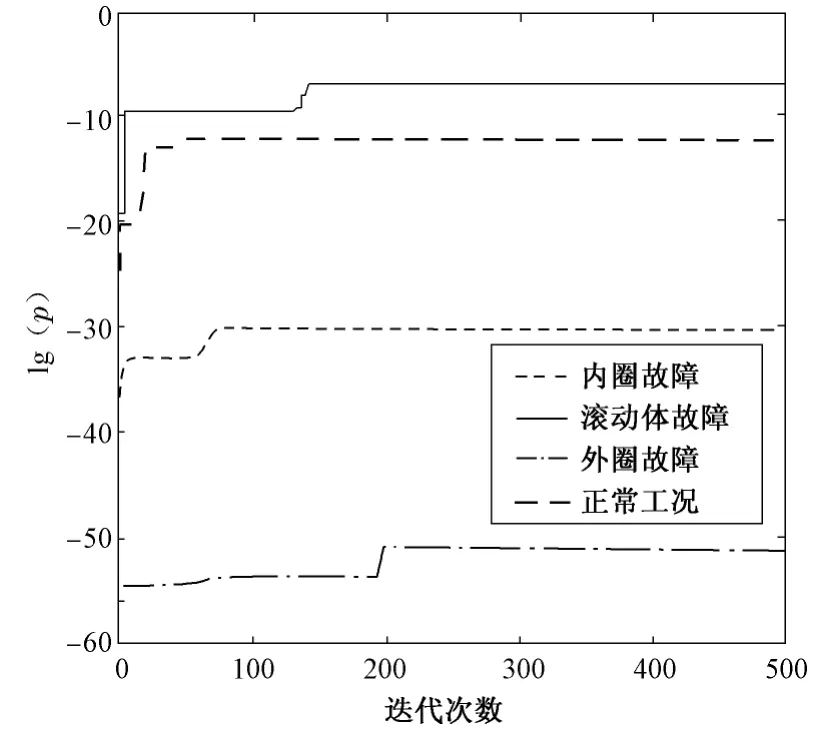
图1 4种故障类型的HMM对数似然率

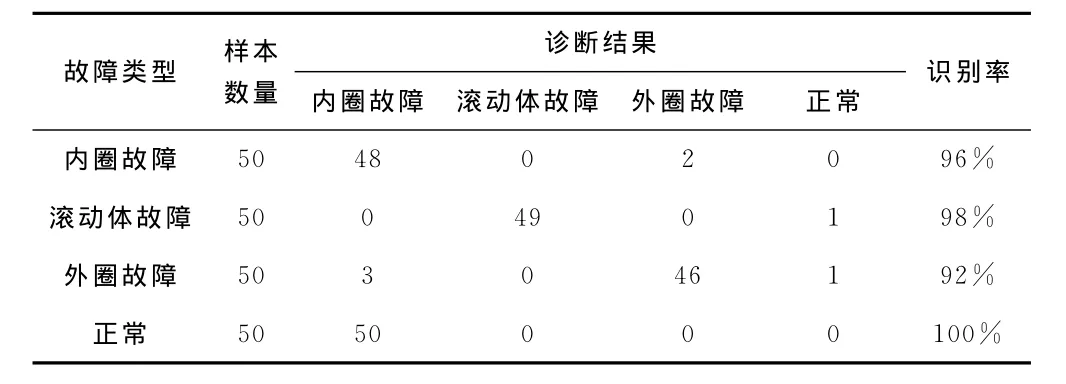
表2 故障诊断的实验结果

6 结语

HMM是故障诊断、语音识别等领域一种有效的分类方法，针对其训练中所采用的Baum－Welch算法对初始参数的选择依赖大、全局寻优能力不足的缺陷，本文提出了基于改进粒子群算法的HMM训练算法，通过对全局最优解加入扰动、对惯性权重加入高斯函数的改进方法，提高了模型的训练算法收敛于全局最优的能力。滚动轴承故障诊断实验表明本文提出的改进训练算法的HMM对轴承故障具有良好的识别率，且4种故障类型的诊断准确率均高于92%，证明了该方法的有效性和实际应用的可行性。

［1］李全.基于 HMM的轴承故障诊断方法［D］.昆明理工大学，2010

［2］王志堂，蔡淋波.隐马尔可夫模型（HMM）及其应用［J］.湖南科技学院学报，2009，30（4）

［3］谢松汕，许宝杰，吴国新，等.基于HMM／SVM的风电设备故障趋势预测方法研究［J］.计算机测量与控制，2014（1）

［4］朱嘉瑜，高鹰.基于改进粒子群算法的隐马尔可夫模型训练［J］.计算机工程与设计，2010，31（1）

［5］张迅，王平，邢建春，等.基于高斯函数递减惯性权重的粒子群优化算法［J］.计算机应用研究，2012，29（10）