基于遗传算法的机械手时间能耗最优平滑轨迹规划

游玮孔民秀肖永强（安徽埃夫特智能装备有限公司，安徽芜湖，4007；哈尔滨工业大学机电工程学院，哈尔滨，5000）

基于遗传算法的机械手时间能耗最优平滑轨迹规划

游玮1孔民秀2肖永强1
（1安徽埃夫特智能装备有限公司，安徽芜湖，241007；2哈尔滨工业大学机电工程学院，哈尔滨，150001）

摘 要

本文提出了一种基于动力学模型的时间与能耗最优的平滑轨迹规划算法，考虑动力学与运动学约束条件，以时间与能量最优为优化目标，建立多关节机器人轨迹规划的数学模型，同时采用改进样条插值函数作为基础函数，保证运行过程中轨迹平滑及起始点与终止点速度、加速度及加加速度为零，之后采用基于遗传学原理的多目标优化算法NSGAII对时间与能耗进行优化，根据Pareto解集选择最优解，并针对一种3自由度重载机器人对提出的算法进行仿真，验证了该方法的可行性。

关键词：机器人，轨迹规划，改进样条函数，多目标优化，时间能量最优

本文是国家自然科学基金项目，项目编号51075086。

0　引言

机器人轨迹规划是指根据一定规则和边界条件产生一些离散的运动指令作为机器人伺服回路的输入指令。规划函数至少需要具有位置指令两阶导数连续，速度指令一阶导数连续，从而可以保证加速度信号连续，加加速度信号有界。不充分光滑的运动指令会激起由于机械系统柔性所产生的谐振，在产生谐振的同时，轨迹跟踪误差会大幅度增加，谐振和冲击也会加速机器人驱动部件的磨损甚至损坏[1]。针对这一问题，相关学者引入高次多项式或以高次多项式为基础的样条函数进行轨迹规划，其中Boryga利用多项式多根的特性，分别采用5次、7次和9次多项式对加速度进行规划，表达式中仅含有一个独立参数，通过运动约束条件，最终确定参数值，并比较了各自性能[2]。Gasparetto采用五次B样条作为规划基础函数，并将整个运动过程中加加速度的平方的积分作为目标函数进行优化，以确保运动指令足够光滑[3]。刘松国基于B样条曲线，在关节空间内提出了一种考虑运动约束的运动规划算法，将运动学约束转化为样条曲线控制顶点约束，可保证角度、角速度和角加速度连续，并在起始点和终止点可以任意配置角速度和角加速度[4]。陈伟华则在Cartersian空间内分别采用三次均匀B样条，三次非均匀B样条，三次非均匀有理B样条进行运动规划，并比较了各自的特点和适用范围[5]。

同时，为提高机器人运行效率、减少能耗并保证轨迹平滑，通常需要对运行时间、运行能耗和加加速度等性能指标进行优化。其中，关于运行时间最优的问题，较为经典的是Kang和Mckay提出的考虑系统动力学模型以及电机驱动力矩上限的时间最优运动规划算法，然而该算法加速度不连续，因此对于机器人来说力矩指令也是不连续的，即加加速度为无穷大，这对于真实的电驱伺服系统来说，是无法实现的，会对系统产生较大冲击，大幅度降低系统的跟踪精度，对机械本体使用寿命也会产生影响[6]。针对上述问题，Constantinescu提出了解决方法，即在考虑动力学特性的基础上，增加对力矩和加加速度的约束，并采用可变容差法对优化问题进行求解[7]。除了以时间为优化目标外，其他指标同样被引入最优运动规划模型中。Martin采用B函数，以能耗最少为优化目标，并将该问题转化为离散参数的优化问题，针对数值病态问题，提出了具有递推格式的计算表达式[8]。Saramago则在考虑能耗最优的同时，将执行时间作为优化目标之一，构成多目标优化函数，最终的优化结果取决于两个目标的权重系数，且优化结果对于权重系数选择较为敏感[9]。

但是采用高次多项式或B样条函数作为基础函数形式较为复杂，计算量大。而对于轨迹优化问题，上述文献基本都是采用将多个优化目标做线性相加转化为单目标优化问题，优化结果严重依赖于各优化目标权重的选择，但是每个优化目标有不同的量纲，简单的线性相加会使得转化后的目标物理意义不明确，从而影响优化的效果。针对上述问题，本文采用改进的样条函数作为基础函数，保证轨迹的平滑性，同时采用一种成熟的多目标遗传算法NSGA-II同时优化时间与能量两个目标，将轨迹规划问题转化为多目标优化问题，根据优化得到Pareto解集选择合理目标量。

1　问题描述

为避免机器人在工作空间轨迹规划中出现的各种问题，同时为避开操作空间中障碍物，通常在操作空间中轨迹初始点至末端点之间选取个关键点，通过机器人末端执行器与各关节间的运动学逆变换，可将工作空间中运动轨迹经过的个点对应为各关节角度。因此机器人轨迹规划问题实质就转化为各关节以何种运动方式平滑的经过关键点，并实现时间能量等指标达到最优。同时，各关节处伺服电机必须满足运动学约束与动力学约束条件。本文以图1所示双平行四边形重载搬运机器人为例，该机器人有3个关节，依据Lagrange方法，机器人动力学方程有如下形式

其中为惯量矩阵，为离心力与惯性力项，为重力项，为关节驱动转矩。

图1　三自由度重载搬运机器人

运动规划目的是在满足运动学与动力学约束前提下实现时间与能量的最优，因此多目标优化问题可表述为：

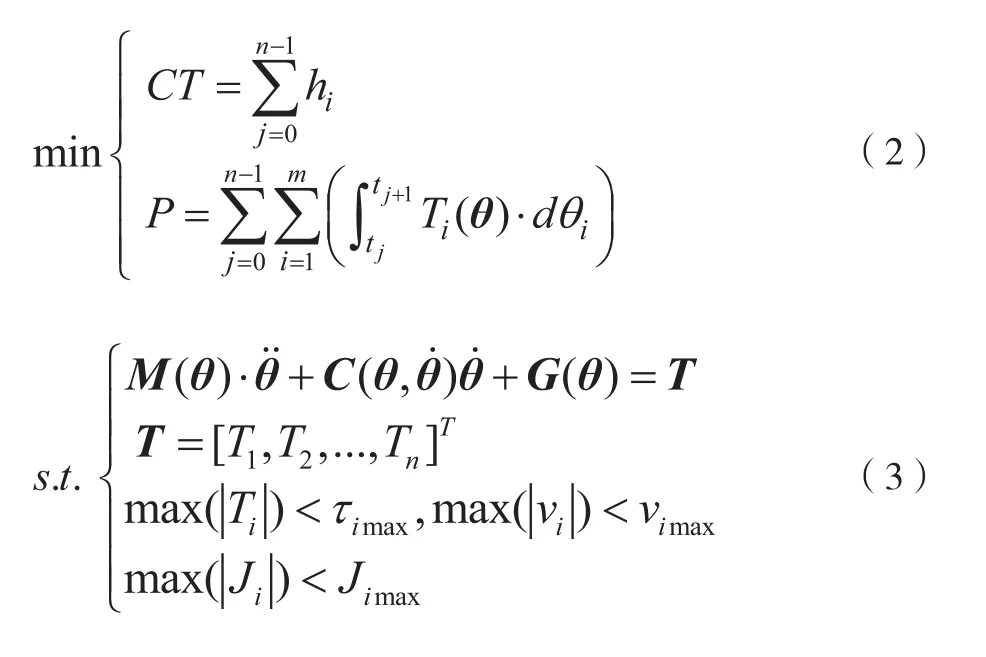
2　改进样条插值基函数

采用三次样条曲线在各预设的过渡点可以保证速度连续，加速度连续。任意两个预设点之间采用三次多项式进行插补：

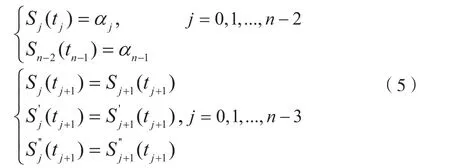
为了保证运动无冲击，首先必须满足在起始点和终止点速度为0，即：

三次样条整体协调方程如下：

虽然在起始点和终止点速度边界可以保证为0，但是其加速度边界不为0，从而导致在起始点和终止点加速度信号为阶跃信号，加加速度幅值为无穷大，这导致对系统低阶振动模态的激振，因此需要对普通的三次样条插值进行修正[10-11]，在起始段和终止段增加辅助项：为多项式形式的辅助项，其必须满足以下约束方程：

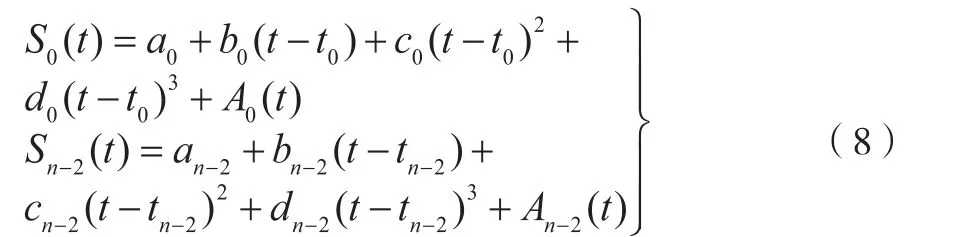
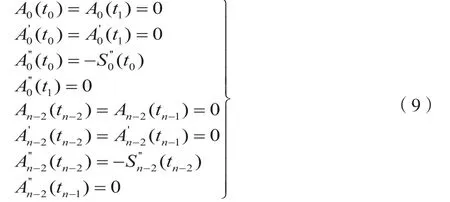
求解上述方程可得辅助表达式如下：

上述改进的三次样条曲线，可以同时保证在起始点和终止点速度加速度为0。

与5次样条曲线相比，上述方程形式简单，计算量小。

3　基于NSGA-II的优化模型求解

对于多目标优化问题，通常存在一个解集。就目标函数而言，这些解之间是无法比较优劣的，其特点是：无法在改进任何目标函数的同时不削弱至少一个其他目标函数，这些解称作Pareto最优解或非支配解。求解多目标优化问题的主要任务是：毫无偏坦地找到尽可能多的具有代表性的符合要求的Pareto最优解，在计算得到均匀分布的Pareto最优解之后，根据具体实际要求，从中客观地选择最满意的优化结果。绝大多数传统的多目标优化求解方法是将多个目标通过转换，使其为一个含有权重系数的单目标优化问题，然后再借助数学规划工具来求解。常见的方法有加权求和法、最大最小法、ε约束法等等[12]。这些传统优化方法存在一定的局限性，首先各指标单位、量纲不相同，无法进行尺度比较，权重选择带有明显的主观性。其次，传统方法对目标函数有凸性、连续性、甚至线性等要求，如加权方法对于Pareto最优阵面的形状很敏感。

进化算法作为一种有效的多目标优化方法已被广泛应用[13-16]。它的优点在于：在优化变量较多的情况下，可处理大规模的搜索空间，在单轮优化期间产生多个最优解或有效解，可有效克服经典方法的局限性。

本文为避免多个优化目标求解下对于权值选择的依赖，采用多目标非支配遗传算法NSGA-II进行求解[17]。NSGA-II算法进化流程及对合并的亲代种群和子代种群进行非支配排序并填充新种群的过程如图2、图3所示，具体过程为：

5） 重复步骤2）- 4），直到达到算法设置的最大迭代次数。

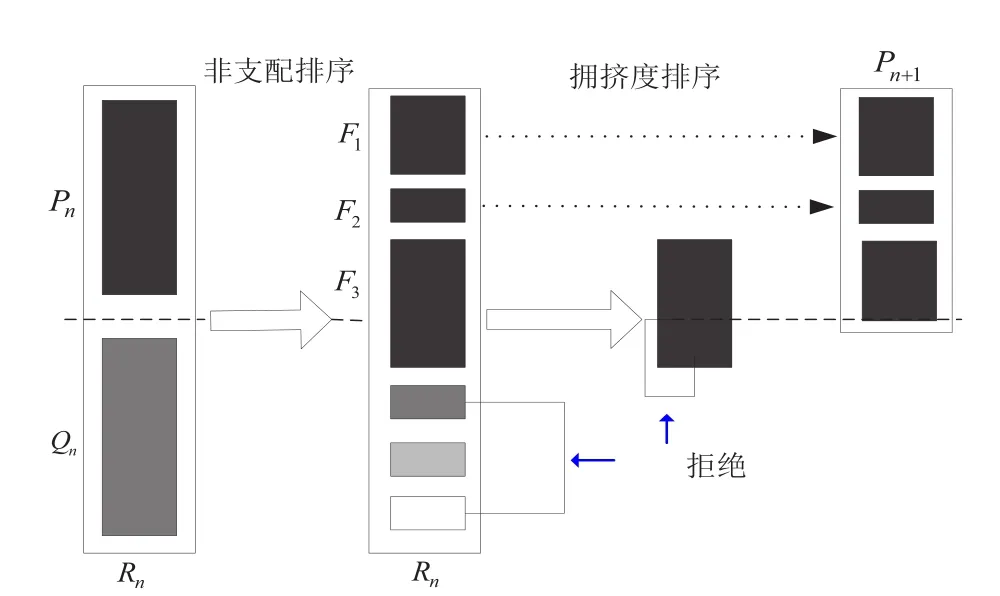
图2　NSGA-II算法种群产生过程图

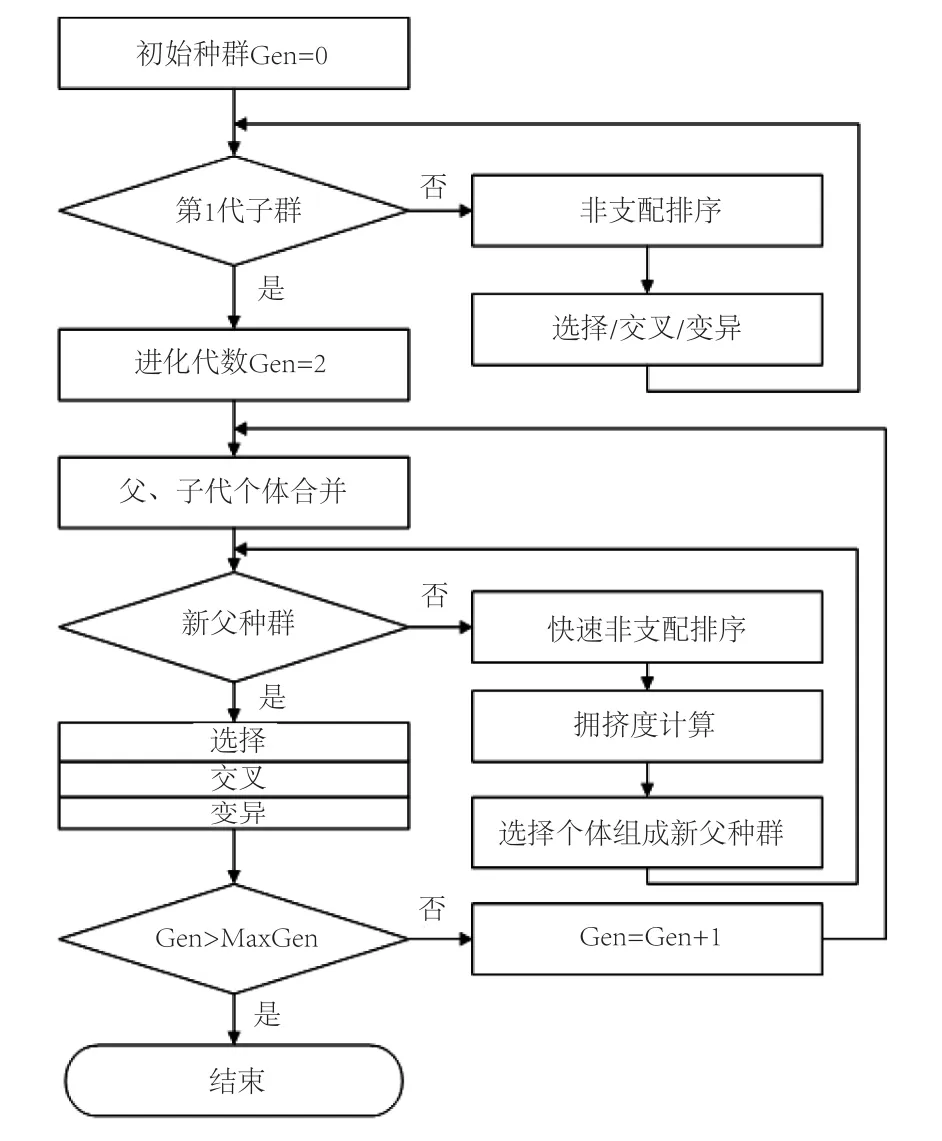
图3　NSGA-II 遗传算法流程图

4　示例与仿真

以上文提到的三自由度重载搬运机器人为例，机器人结构简图见图4，由于该结构为双平行四边形结构，运动学与动力学分析所需的参数如表1所列。整个优化运动算法计算示例如下，现在存在5个预设点（见图6(a)，红点标出）。不加优化，各点之间的运行时间为0.5s, 0.5s, 0.25s, 1.25s。总运行时间为2.5s。当种群数量设为1000，进化代数设为50代。整个进化所得结果见图5，整个优化求解耗时2.4s。得到的Pareto的解集如表2所示,其中第一组解被选为最终解。

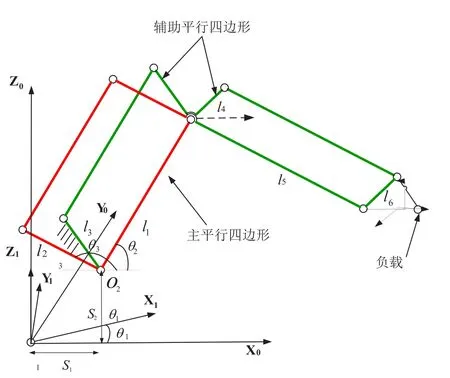
图4　机器人结构简图

表1　三自由度重载机器人基本参数/mm

表2　NSGA-II获得最优运动规划参数Pareto解集

图5　含有两个目标的Pareto解集

图6　运行轨迹和运动间隔分配

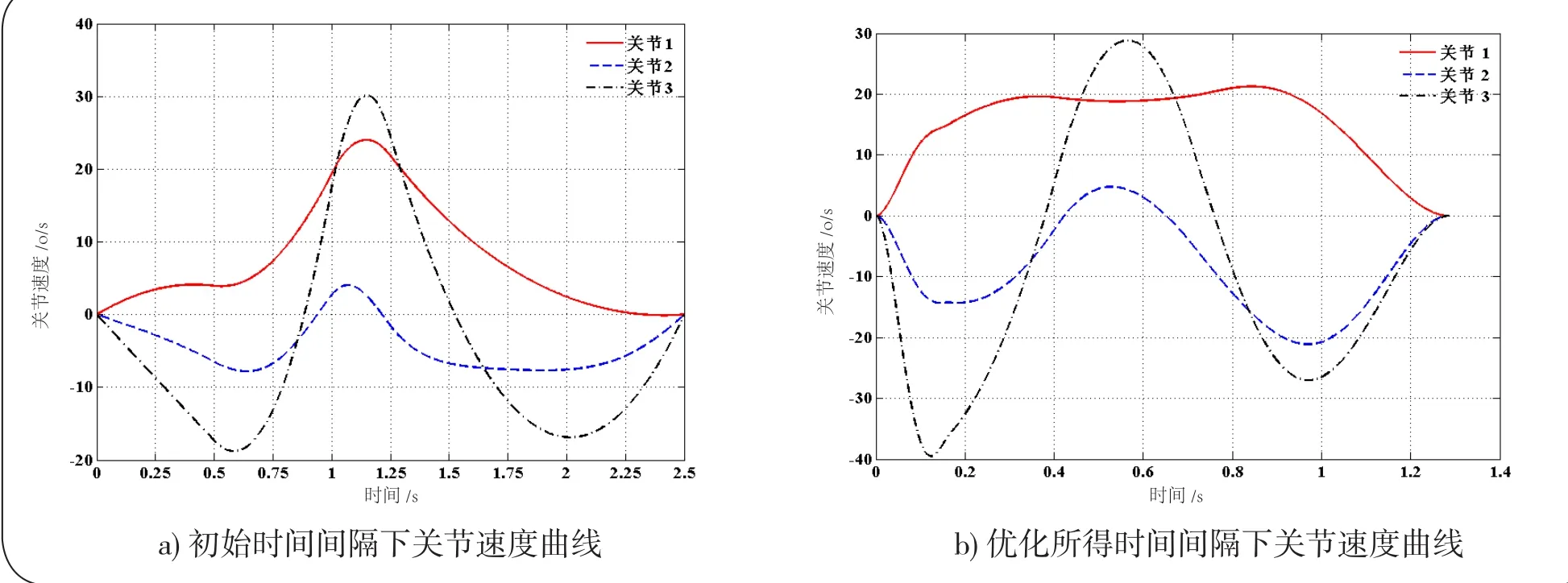
图7　关节速度比较

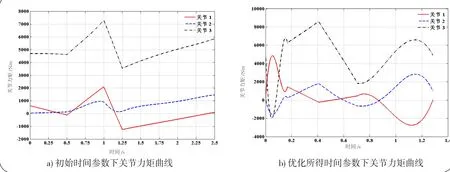
图9　关节加速度比较

从图6可知，采用优化所得时间间隔后执行完整个轨迹段所需时间是1.2848s，生产效率提高近一倍。同时从图5可知总能耗为2606J，增加生产效率的同时，能耗却降低20%。尽管优化所得运动要比初始运动快很多，但是每个关节的速度和力矩值均未上升很多，都在允许范围内，见图7和图8。由图9可知，在初始参数下，运动起始点和终止点的加速度均不为0，从而导致加速度为无穷大。对系统将产生冲击。而采用改进Cubic样条计算所得的优化参数后，起始点和终止点加速度值为0，整个运动过程足够平滑。

5　结论

采用改进样条曲线的机械手轨迹规划方法保证了关节轨迹的充分平滑，保证了起始点与终止点的速度加速度为0，从而保证了整个运行阶段加加速度有界，克服了三次样条曲线插值起始点与终止点加速度突变的影响，同时取得了比B样条插值或高次多项式插值更简单的形式。

采用NSGA-II多目标优化算法对时间与能耗同时优化，使得优化目标物理意义明确，避免了运动规划传统优化算法过于对各目标权重依赖及权重选取的随意性，可以根据需要从Pareto解集中选择多组解进行比较与优选。

参考文献

[1] BARRE P J, BEAREE R, BORNE P, et al. Influence of a Jerk Controlled Movement Law on the Vibratory Behavior of High Dynamics Systems [J]. Journal of

Intelligent & Robotic Systems Theory & Applications, 2005, 42(3): 275-293.

[2] BORYGA M, GRABOS A. Planning of manipulator motion trajectory with higher-degree polynomials use [J]. Mech Mach Theory, 2009, 44(7): 1400-1419.

[3] GASPARETTO A, ZANOTTO V. A new method for smooth trajectory planning of robot manipulators [J]. Mech Mach Theory, 2007, 42(4): 455-471.

[4] 刘松国. 六自由度串联机器人运动优化与轨迹跟踪控制研究[D].杭州:浙江大学, 2009.

[5] 陈伟华. 工业机器人笛卡尔空间轨迹规划的研究[D]. 广州:华南理工大学, 2010.

[6] SHIN K G, MCKAY N D. Minimum-Time Control of Robotic Manipulators with Geometric Path Constraints[J]. IEEE Transactions on Automatic Control, 1985, 30(6):531-541.

[7] CONSTANTINESCU D, CROFT E A. Smooth and Time-optimal Trajectory Planning for Industrial Manipulators Along Specified Paths [J]. Robotic Systems, 2000, 17(5): 233-249.

[8] MARTIN B J, BOBROW J E. Minimum-Effort Motions for Open-Chain Manipulators with Task-Dependent End-Effector Constraints [J]. The International Journal of Robotics Research, 1999, 18(2): 213-224.

[9] SARAMAGO S F P, STEFFEN V. Optimization of the Trajectory Planning of Robot Manipulators Taking into Account the Dynamics of the System [J]. Mech Mach Theory, 1998, 33(7): 883-894.

[10] 张小江, 高秀华. 三次样条插值在机器人轨迹规划应用中的改进研究[J].机械设计与制造, 2008, 9(2): 170-171.

[11] BOOR C D. A Practical Guide to Splines [M]. New York: Springer, 2001.

[12] MARLER R T, ARORA J S. Survey of Multi-Objective Optimization Methods for Engineering [J]. Structural & Multidisciplinary Optimization, 2004, 26(6):369-395.

[13] LEUNG Y W, WANG Y P. Multiobjective Programming Using Uniform Design and Genetic Algorithm [J]. IEEE Transactions on Systems Man and Cybernetics Part C-Applications and Reviews, 2000, 30(3): 293-304.

[14] COELLO C A C. An updated survey of GA-based multiobjective optimization techniques [J]. Acm Computing Surveys, 2000, 32(2): 109-143.

[15] CUI L L, XIAO Z Q. Optimum Structure Design of Flexible Manipulators Based on GA[C]// Intelligent Transportation Systems. IEEE, 2003,2:1622-1626.

[16] ZHANG X, NELSON C A. Multiple-Criteria Kinematic Optimization for the Design of Spherical Serial Mechanisms Using Genetic Algorithms [J]. Mechanical Design, 2010, 133(1):819-827.

[17] DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II [J]. IEEE T Evolut Comput, 2002, 6(2): 182-197.