黄土高原旱区浅层黄土水分场的数值分析

李彦龙, 王铁行, 王娟娟

(西安建筑科技大学 土木工程学院, 陕西 西安 710055)

黄土高原旱区浅层黄土水分场的数值分析

李彦龙, 王铁行, 王娟娟

(西安建筑科技大学 土木工程学院, 陕西 西安 710055)

摘要：[目的] 研究黄土高原浅层土体水分场在春季连续干旱条件下的动态变化。[方法] 通过非饱和黄土二维非稳态流有限元控制方程对黄土高原浅层土体水分场在不同气象条件下的动态变化进行数值计算。[结果] 在连续干旱条件下水分场的计算结果与实测结果较为一致，受蒸发影响的土层最大厚度为1.8 m，连续3个月的干旱使其平均含水率降低至7.9%，土壤蒸发强度随着含水率的减小而减小。强度较小且分散的降雨对于缓解连续干旱期黄土高原土壤干旱基本无效，大强度集中降雨只能在短时间内缓解土壤旱情。[结论] 数值计算结果可为实际工程中植被类型的选择以及灌溉时间的把握所参考。

关键词：连续干旱期; 黄土高原; 水分场; 数值分析

黄土高原路基、市政等工程领域的植物防护及绿化工程规模随着西部大开发战略的实施而日益增大[1]。以干旱、半干旱地区为主的黄土高原，作为植物生长和防护工程载体的浅层黄土，其土壤水资源是植被承载力的关键因素[2-4]。黄土高原水分循环以上行蒸发和降雨入渗为主，大气环流特征使其降水量在年内分布极不均匀，冬干春旱，夏秋季降雨集中[5]。对植被建设以及植物防护工程而言，春季连续干旱气象条件下最容易导致植被萎蔫死亡。对黄土高原浅层土体水分场在春季连续干旱气候条件下的动态变化进行研究，可以为实际工程中植被类型选择和灌溉时间的把握上提供相关资料。

浅层土体水分场在气象条件下的动态变化是SPAC系统土壤水动力学的一部分，同时也是岩土工程、环境科学、水利工程、地学和土壤学等学科的交叉研究课题，以土壤学为基础的单一过程的裸地蒸发[6-8]和降雨入渗[9-11]已有较多的研究，包括经验法和机理法。经验法在使用过程中具有区域局限性，其虽然可以计算累计入渗或蒸发量，但是不能计算土体内任一点的水头；以土壤学为代表的机理法主要为IRE方法[12]和以SWMS-2D为代表的有限元方法。

但是通过有限元方法并针对黄土高原浅层土体水分场在气象条件下的动态变化却少有研究。因此，本文拟通过岩土工程中的二维非稳态流有限元控制方程并结合实测资料对黄土高原浅层土体水分场在连续春旱条件下的水分场进行分析，并通过数值计算来探明不同条件下的降雨对缓解春旱的效用。

1研究区概况

实测场地为陕北米脂县杨家沟镇何家岔，地理坐标为东经109°49′—110°29′，北纬37°39′—38°05′，土壤以黄绵土为主；年平均温度为8.9 ℃，日照时数为2 716 h，年平均降雨量为420.2 m，无霜期160～170 d；海拔951～1 029 m，由于长期粗放式经营导致该区自然植被稀少。实测时间为2013年3—5月(共12周)，期间该地区累计降雨为10 d，累计降雨量为45 mm。其中，有效降雨为5 d，有效日均降雨量9 mm/d。因此，实测期间的气象状况基本可以满足连续干旱的条件。

土壤水的受力状况决定了它并不能完全被植物吸收和利用，只有介于萎蔫湿度和田间持水量之间的土壤水分才能被植物根系吸收和利用。介于该区间的土壤水又可分为难效水(萎蔫湿度到生长阻滞含水率，小于田间持水量的60%)，中效水(田间持水量的60%～80%)和易效水(田间持水量的80%～100%)，低于凋萎湿度的土壤水则为无效水。陕北米脂地区土壤难效水(6.8%～9.1%)，中效水(9.1%～12.4%)和易效水(12.4%～15.2%)[13]。用土钻在标准地内取样测定裸地的天然含水率，分别在3月1号。3月28号,4月28号，5月28号取一次样，取样深度为6 m，0—1 m土层以0.1 m为一个层次，1—6 m土层每0.2 m为一个层次，共计35个层次，通过烘干法测含水率。

2计算模型及参数选取

2.1　计算模型

连续干旱条件下，浅层黄土水分场中任一点的水头和渗透系数均随着随时间而变化，因此浅层黄土中的水分场为非稳态流，其控制方程为[14]：

(1)

式中：[D]——刚度矩阵； [E]——容量矩阵； [F]——流量列阵； {h}——水头列阵。

采用向后差分格式，式(1) 即为：

(2)

基质吸力模型采用van Genuchten模型，其表达式如下：

(3)

式中：θ——体积含水率；θs——饱和含水率；θr——残余含水率；h——吸力水头(m)；α，m，n——系数，m=1-1/n。

对黄土而言，式(3) 中相关参数可按参考文献[15]确定：

θr=-0.38+0.36ρd

(4)

θs=1-0.38ρd

(5)

α=exp〔(8.98-0.08T)+(-9.36+0.07T)ρd〕

(6)

(7)

(8)

将公式(3) 带到式(8) 中可得：

(9)

参考文献[16]给出了非饱和黄土水分扩散率与含水率之间的关系：

D=exp(aθ2+bθ+c)

(10)

式中：D——非饱和黄土的水分扩散率；a，b，c——系数，其中，a=84.5ρd-57.1，b=-56ρd+61.8，c=5.7ρd-12。

非饱和黄土比水容C式(11)表示：

(11)

式中：ρw——水的密度；g——重力加速度。

非饱和土的渗透系数与扩散率和比水容有如下关系：

kw=D×C

(12)

将公式(10)，(11)带入式(12)可得：

(13)

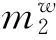
2.2　水头的确定

土体中的水头通常可以表达为：

h=hg+hm+hp+hs+hT

(14)

式中：h——总水头；hg——重力水头；hm——基质吸力水头；hp——压力水头；hs——渗透水头；hT——温度水头。

温度水头和溶质水头通常可以忽略，对非饱和土中的水分迁移而言，认为土体所有孔隙与大气是联通的，因此压力水头为零。因此只需考虑重力水头和基质吸力水头，式(14)可以简化为：

h=hg+hm

(15)

其中，重力水头按位置确定，吸力水头由VG模型确定。

2.3　有限元模型

计算深度为6.0 m，所采用的三节点三角形单元均为直角三角形，共计划分60层，0—1.0 m深度内，每层0.05 m；1.0—3.0 m深度内，每层0.1 m，3—6 m深度内，每层0.15 m；模型宽0.35 m，共计7列，每列0.05 m。该模型共计840个单元，488个节点。为了减小计算误差，取每层各个节点的算术平均值作为最终计算结果。

2.4　计算方案及边界条件

土体干密度统一取1.4 g/cm3，根据3月1号实测土层含水率，计算时初始含水率取12.4%(中效水上限)，计算深度内土体温度统一取15 ℃[17]。

3种计算方案如下：

(1) 1～12周连续干旱。

(2) 第5周连续降雨，日均降雨量25.0 mm/d，其他时间段内连续干旱。

(3) 第5周连续降雨，日均降雨量50.0 mm/d，其他时间段内连续干旱。

上述3种计算方案均采取流量边界(Neumann type)。降雨入渗时，流量为正，其流量即为日均降雨量，认为所有雨水全被入渗土壤中，忽略地表径流的影响；蒸发时，流量为负，其流量可按式(16)确定[18]：

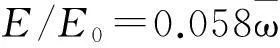
(16)

3计算结果

图1(a—c)为方案1的计算结果。(1) 连续干旱条件下，土层实测结果与数值计算结果较为一致。受蒸发影响的土层深度为0—1.8 m。这一计算结果与陕北米脂地区土壤蒸发规律相吻合，即蒸发影响深度为2.0 m，2.0 m以下的土层为相对稳定层。

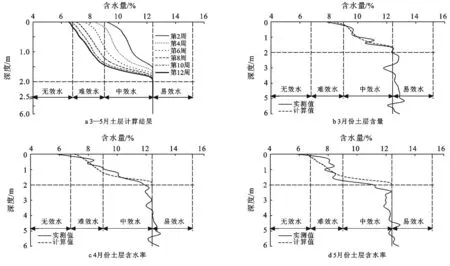
图1　3-5月土层含水率计算方案1的计算值

同时植被根系也广泛地分布在0—2.0 m土层中，因此0—2.0 m土层的含水率分布情况对植被的生长起到至关重要的作用。拟合得到了蒸发影响深度与随时间的变化关系：

z=1.82-0.74·e-t/3.43

(17)

式中：z——影响深度(m)；t——蒸发时间(周)。

(2) 0—1.8 m土层的含水率随着蒸发的不断进行而减小，其中0—1.0 m土层的含水率变化最为显著。连续3个月的干旱蒸发使土壤0—1.8 m平均含水率从蒸发初期的12.4%下降到蒸发末期的7.9%。当蒸发进行到第6周(4月中旬)时，0—0.85 m土层已经进入难效水的区间。此时已形成轻度干层，对于根系发育较浅的植被而言，其生长开始受到阻碍。当蒸发进行到第8周时，进入难效水的土层厚度为0—1.2 m。当蒸发进行到第10周时，0—1.4 m的土层水分为难效水。拟合得到0～1.8 m平均含水率随时间的变化关系：

(18)

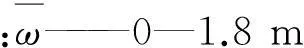
(3) 蒸发强度随着土壤含水率的下降而减小，同时其蒸发强度也随着蒸发时间的增长而减小。主要原因是土壤中含水率随着土壤中水分的不断蒸发而下降，毛管水开始变的不连续，同时在表层0—0.1 m形成干层。当表层形成干层后，土壤表层导水率接近0，此时水分只能在干土层以下的表面气化，并以气态水的方式向周围大气中扩散。

图2为方案2的计算结果。雨水入渗深度为0.55 m；降雨后1周内(第6周)土壤入渗深度内的水分大量蒸发，当蒸发进行到第7周(雨后2周)时，0—1.8 m土层平均含水率为9.2%已经小于降雨前(第4周)的9.9%。

图2　3-5月土层含水率计算方案2的计算值

由此表明，上述次降雨条件下裸地土壤水分只能得到短暂的补给，对缓解深层土壤的干旱基本无效，大部分入渗雨水将很快消耗于蒸发过程中，计算结果表明该蒸发消耗过程不超过1.5周。然而在以米脂县为代表的黄土高原旱区，其春季实际累计平均降雨量只有45 mm(29 a统计结果)远小于数值计算中所采用的175 mm降雨量，且其有效降雨时间比较分散，如此气象条件下，本就稀少的降雨会很快地被蒸发消耗殆尽，对于缓解黄土高原旱区春季旱情效果甚微。

图3为方案3的计算结果。从图3中可以看出，雨水的入渗深度为1.1 m；雨后2周(第7周)土层0—1 m含水率仍处于中效水；雨后3周(第8周)土壤0—1.8 m平均含水率为10.1%仍高于雨前的9.8%；表明此种类型的降雨条件可以有效地缓解浅层土壤的干旱，尤其对于植被根系广泛分布于0—1 m土层。

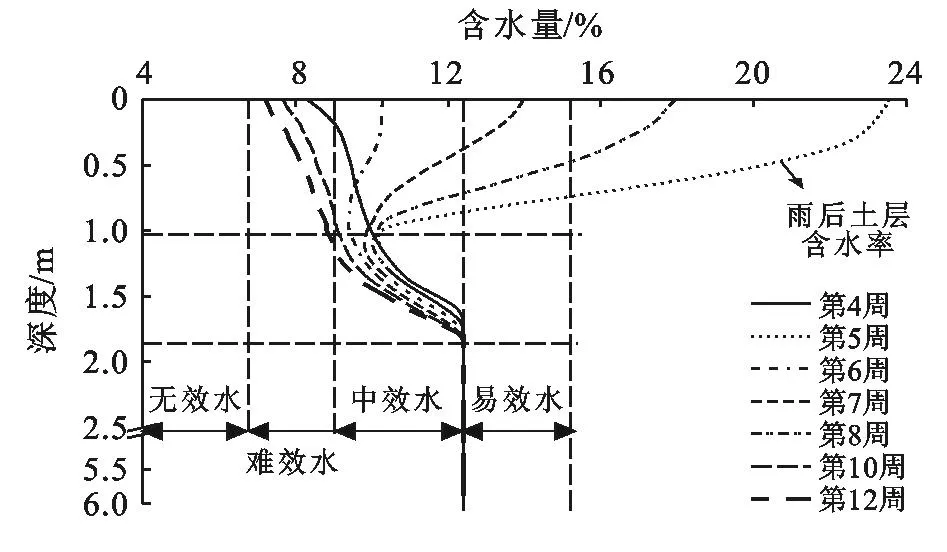
图3　3-5月土层含水率计算方案3的计算值

4结 论

根据非饱和黄土二维非稳态流有限元控制方程，对连续干旱条件下以及不同强度降雨条件下黄土高原旱区的水分场进行了数值计算。主要结论如下：对植被生长而言其最不利水分场为连续干旱条件下；对于黄土高原旱区而言，强度较小的降雨对于缓解土壤干旱基本无效；大强度集中降雨只能在一段时间内缓解土壤旱情。上述结论是基于裸地蒸发和降雨入渗，对于有植被覆盖的黄土高原浅层黄土而言，需要进一步研究；针对大强度集中降雨时有地表径流和地表积水的情况也仍需进一步研究。计算时所采用的边界条件是基于陕北米脂地区，对于黄土高原其他地区的裸地蒸发和降雨入渗，可以根据该地区的实际气象条件来确定边界条件。

[1]杨光,孙保平,赵廷宁,等.黄土丘陵沟壑区退耕还林工程植被恢复效益初步研究[J].干旱区资源与环境,2006,20(2):165-170.

[2]何永涛,李文华,李贵才,等.黄土高原地区森林植被生态需水研究[J].环境科学,2004,25(3):35-39.

[3]许炯心.黄土高原植被—降水关系的临界现象及其在植被建设中的意义[J].生态学报,2005,25(6):1233-1239.

[4]张建兴,马孝义,赵文举,等.黄土高原地区水资源承载力动态变化分析：以山西、陕西、宁夏、甘肃4省为例[J].干旱区研究,2009,26(1):115-119.

[5]邵明安,郭忠升,夏永秋,等.黄土高原土壤水分植被承载力研究[M].北京：科学出版社,2010.

[6]Campbell G S. Soil physics with BASIC: transport models for soil-plant systems[M]. Elsevier, 1985.

[7]Yanful E K, Mousavi S M. Estimating falling rate evaporation from finite soil columns[J]. Science of the Total Environment, 2003,313(1):141-152.

[8]Han H, Felker P. Estimation of daily soil water evaporation using an artificial neural network[J]. Journal of Arid Environments, 1997,37(2):251-260.

[9]Ma Ying, Feng Shaoyuan, Su Dongyuan, et al. Modeling water infiltration in a large layered soil column with a modified Green-Ampt model and HYDRUS-1D[J]. Computers and Electronics in Agriculture, 2010,71(S):40-47.

[10]Rao M D, Raghuwanshi N S, Singh R. Development of a physically based 1D-infiltration model for irrigated soils[J]. Agricultural water management, 2006,85(1):165-174.

[11]Gencoglan C, Gencoglan S, Merdun H, et al. Determination of ponding time and number of on-off cycles for sprinkler irrigation applications[J]. Agricultural Water Management, 2005,72(1):47-58.

[12]Lee D H, Abriola L M. Use of the Richards equation in land surface parameterizations[J]. Journal of Geophysical Research: Atmospheres (1984—2012), 1999,104(D22):27519-27526.

[13]杨文治,邵明安.黄土高原土壤水分硏究[M].北京：科学出版社,2000.

[14]Ng C W W, Menzies B. Advanced unsaturated soil mechanics and engineering[M]. CRC Press, 2007.

[15]王铁行,卢靖,岳彩坤.考虑温度和密度影响的非饱和黄土土—水特征曲线研究[J].岩土力学,2008,29(1):1-5.

[16]卢靖.非饱和黄土水分迁移问题的试验研究[D].西安:西安建筑科技大学,2006.

[17]王铁行,刘自成,岳彩坤.浅层黄土温度场数值分析[J].西安建筑科技大学学报:自然科学版,2007,39(4):463-467.

[18]王铁行,陈晶晶,李彦龙.非饱和黄土地表蒸发的试验研究[J].干旱区研究,2014,31(6):985-990.

[19]Fredlund D G, Rahardjo H. Soil Mechanics for Unsaturated Soils[M]. John Wiley & Sons, 1993.

Numerical Simulation of Moisture Field in Shallow Loess of Loess Plateau During Continous Drought

LI Yanlong, WANG Tiehang, WANG Juanjuan

(SchoolofCivilEngineering,Xi’anUniversityofArchitecture&Technology,Xi’an,Shaanxi710055,China)

Abstract：[Objective] To analyze the dynamic change characteristics of moisture field in shallow loess of Loess Plateau during the continuous drought.[Methods] The dynamic changes of moisture field in shallow loess were calculated numerically by the unsaturated loess unsteady flow 2 dimension finite element control equation under the three different meteorological conditions. [Results] The calculation results were consistent with the measured results during the continuous drought, the thickness of loess affected by the evaporation was 0～1.8 m. Three consecutive months of drought makes its average moisture content dropped to 7.9%, the evaporation intensity of the loess decreased with the decrease of moisture content. The scattered and low intensity rainfall for alleviating continuous drought is invalid basically. The concentrated and intensive rainfall can alleviate soil drought only in a short period.[Conclusion] The results of numerical calculation can provide references for the choice of vegetation types and irrigation time.

Keywords:continuous drought; Loess Plateau; moisture field; numerical simulation

文献标识码：B

文章编号：1000-288X(2015)01-0148-05

中图分类号：TU441

收稿日期：2014-01-10修回日期：2014-01-20

资助项目：国家自然科学基金项目“黄土高原旱区浅层土体水分场随气候变化机理及数值模拟”(51078309)

第一作者：李彦龙(1985—),男(汉族),河南省南阳市人,博士研究生,研究方向为黄土力学与工程。E-mail:liyanlong1229@163.com。