模糊评判法在煤矿采空区稳定性评价中的应用

罗 东 海

(中国煤炭地质总局 煤航地质勘查院, 陕西 西安 710054)

模糊评判法在煤矿采空区稳定性评价中的应用

罗 东 海

(中国煤炭地质总局 煤航地质勘查院, 陕西 西安 710054)

摘要：[目的] 探讨运用模糊评判法评价采空区稳定性的可行性及实用价值。[方法] 将影响煤矿采空区稳定性因素分为地质因素、采空因素、外部因素及时间因素4大因素，进一步细分为煤层埋藏特征、地质构造特征、覆岩物理力学性质、水文地质特征等8大要素，细化出地层、煤层埋藏深度、松散层厚度等22项因子。将采空区稳定性级别分为：较不稳定、不稳定及极不稳定3个级别，采用模糊评判法，建立煤矿采空区稳定性评价的模糊层次分析模型，构建对比矩阵，并以凤凰山矿凤2采空区为例，对其稳定性进行评价。[结果] 研究区稳定性级别属于极不稳定区，与现场调查情况基本相符。[结论] 运用模糊评判法进行采空区的稳定性评价具有可行性，可运用到其他类似采空区稳定性评价中指导矿区合理规划和开采，具有实用价值。

关键词：采空区; 稳定性评价; 模糊评判法; 模型

长期以来，中国一直是以煤炭为主要能源结构的发展中国家，大规模、持续的煤炭资源开采，在以煤炭开采为主的一些矿业城市或能源基地形成了大面积采空区，可能或已经诱发了大量采空塌陷、崩塌及地裂缝等一系列地质灾害，威胁到人民群众生命财产安全，严重制约了当地的经济社会发展。据统计，仅山西省采空区面积就已达到近2.00×104km2，占全省面积的1/7。伴随着城市发展建设步伐的加快，建设用地紧张问题日益突出，就不可避免地将在采空区塌陷区进行一系列基础设施建设[1]，而采空区稳定性评价将是采空区地表进行基础设施建设的前提条件。

对采空区的研究已有近百年历史，采空区稳定性评价方法也逐步由定性评价发展至半定量、定量评价。常用的方法有工程地质类比法[2]，力平衡分析法[3]，附加应力分析法[4]及数值模拟分析法[5-6]等，这些方法有些是定性评价方法，有些仅从力学角度分析，并不能考虑多因子共同作用、影响下的采空区稳定性，与复杂的地质实际情况亦有不同。煤矿采空区稳定性评价应与开采煤层的厚度、埋深、上覆岩层的岩性、厚度、地质构造、水文地质条件以及煤矿开采方法、开采面积、开采次数、顶板管理方法等多因素密切相关，是一项复杂的系统工程，影响因素众多且复杂，各因素对稳定性影响程度也不尽相同，相互之间又存在一定联系性，依据这一特点，可采用模糊层次分析法对采空区进行综合评价。

本文在充分考虑煤矿采空区影响因素基础上，建立煤矿采空区稳定性评价模型，对各评价因子进行两两比较，基于层次分析法(AHP)确定权值，将影响采空区稳定性的各定性因子定量化、归一化，并以山西省晋城市凤凰山矿采空区为例，采用Ⅲ级模糊综合评判法评定采空区稳定性级别。

1煤矿采空区稳定性评价的模糊层次分析法原理

模糊综合评价法是以隶属度来描述模糊界限的。由于影响采空区因素的复杂性、层次性、模糊性以及评价影响因素的模糊性或不确定性、定性指标难以定量化等一系列问题，采用经典数学模型难以统一量度。而建立在模糊集基础上的模糊综合评判法一方面既可顾及评判对象的层次性、多样性及复杂性，又可使评价标准、影响因素的模糊性得以体现，还可以做到定性和定量因素相结合，扩大信息量，使评价精度得以提高；另一方面，在评价中又可以充分发挥人的经验优势，使评价结果更客观，更加符合实际情况。

1.1　多级模糊数学综合评价基本原理

综合评价是人类一种重要的智力活动，它对某事物根据多种因素(或多个评判者)分别给出评判结果，最终得出一个综合各因素(或多个评判者)的评判结果。可作如下描述：设U和V是两个有限的论域：U={u1，u2，…，un}，V={v1，v2，…，vm}，其中U称为评判因素集合(或评判者集合)，V称为评语集合(或评价结果集合)。若对单因素u1∈U而言，对某事物给出的模糊评判用一个在评语集(或评价结果集)V上的一个模糊集表示，即：

(μi1/v1，μi2/v2，μi3/v3，μi4/v4…，μim/vm)

式中：0≤μi1≤1，i=1，2，3，…，n，j=1，2，3，…，m。这样就得到一个对该事物的评判矩阵E：

若各评判因素(或各评判者)的权重(或权威程度)用U上的一个模糊集表示，即：

(x1/u1，x2/u2，x3/u3，…，xn/un)

(xi≥0； i=1，2，3，…，n)

式中：xi——第i个因子对应的权；则，对该事物的综合评判结果为V上的模糊集：

(y1/v1，y2/v2，y3/v3，…，yn/vn)或向量Y=(y1，y2，y3，…，ym)，其中，Y=X·E，为一适当的模糊运算“+(加法)与×(乘法)”等。

1.2　多级模糊数学综合评价的过程与步骤

1.2.1建立煤矿采空区稳定性模糊综合评判模型充分考虑影响煤矿采空区稳定性各因素，建立采空区多级模糊综合评价流程模型图(图1)。模型包括目标层—煤矿采空区稳定性评价、因素层、要素层及因子层等4层，共包括地质因素、采空因素、外部因素及时间因素等4大因素，各因素下细分了煤层埋藏几何条件、地质构造及岩石物理力学性质等8大要素，各要素下细化出地层、埋藏深度、松散层厚度等22个因子。其中，采空年限结合工程实践及相关规范[7]，当采空年限大于3a时，对采空区稳定性影响程度为轻度，采空年限为2～3a时，影响程度为中度，采空年限小于2a，影响程度为重度。该模型较全面、系统概况了影响煤矿采空区稳定性的主要因素。

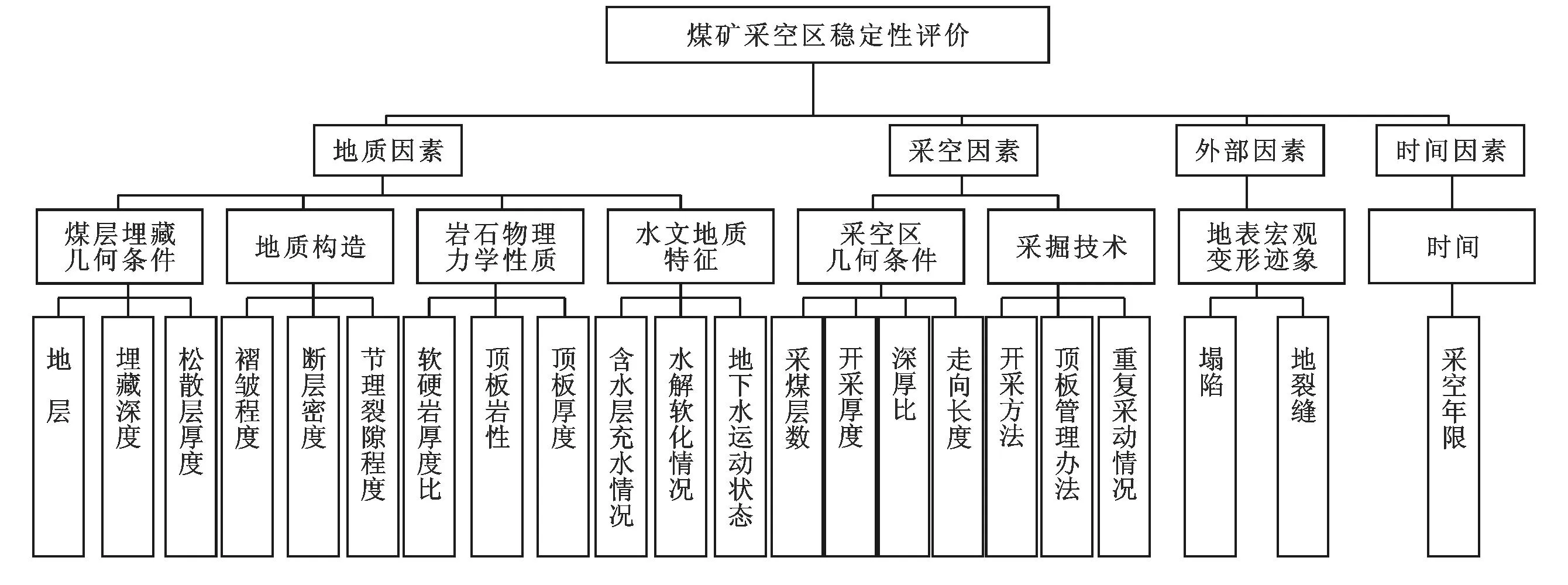
图1　煤矿采空区稳定性Ⅲ级模糊综合评判模型

1.2.2确定评价语集确定煤矿采空区评语(评价标准)集合V，这里采用Ⅲ级划分法，即较不稳定、不稳定、极不稳定，则评价集为：

V={V1,V2,V3}=(较不稳定，不稳定，极不稳定)

1.2.3确定各层权值在多因子评判中，因不同因子在稳定评价中的作用不同，应取不同的权值。权重的赋值是本数学模型计算的关键问题之一，可采用层次分析法确定各因子权重值。

层次分析法(analytical hierarchy process,AHP)，是20世纪70年代美国运筹学家Satty[8]提出的一种定性与定量分析相结合的多目标决策分析方法论。采用层次分析法确定权重的基本步骤包括[9-11]： (1) 建立层次分析模型，这里同模糊综合评判模型，本模型中包括目标层、因素层、要素层及因子层4层； (2) 构建对比矩阵，在同一层中进行两两对比，依据1—9标度法[12](表1)，对各因子进行两两比较，综合评价； (3) 计算权重系数； (4) 进行一致性检验。采用层次分析法确定权重的方法具有简洁、灵活及系统的优点，详细步骤不再赘述。

1.2.4确定各评价因子隶属度所选取评价因子有定性的，也有定量的，不同形式因子隶属度取值不同。结合对晋城市及周边煤矿采空区基本特征的统计，参考相关规范，可综合确定各因子在不同稳定性阶段“阀值”如表2所示。

隶属度的确定目前还没有一套成熟稳定的方法，大多数方法主要还停留在经验和试验阶段，包括模糊统计法、例证法、专家经验法及隶属函数法等[11]。结合采空区稳定性研究特点，定量因子隶属度可采用模糊统计法确定。以埋藏深度因子为例，分别统计采空区煤层埋藏深度>150，50～150及<50 m的面积，并进行归一化处理，即可得出该采空区煤层埋藏深度因子隶属度，其他定量因子亦可由此确定。定性因素的隶属度取值可参考表3确定。

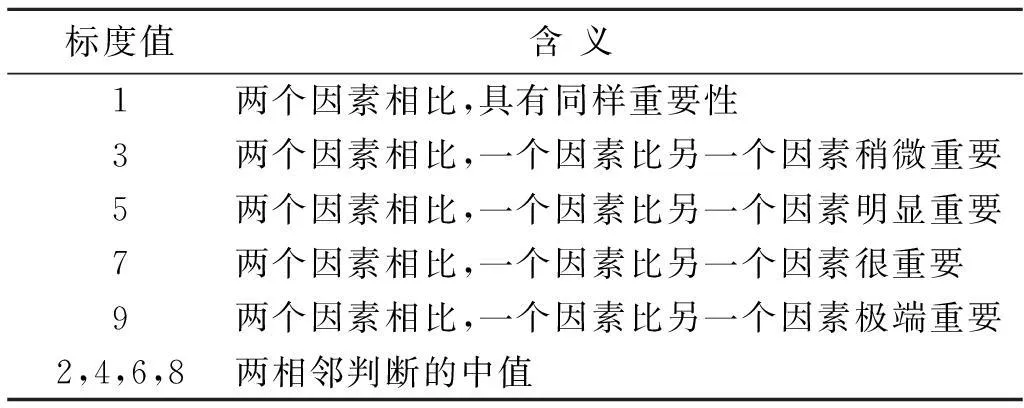
表1　T·L·Satty标准及标度含义

表2　煤矿采空区稳定性评价因子分级

进行Ⅰ级模糊综合评价，得出Ⅱ级模糊综合评价的隶属度，依次逐级进行评价，最后得出评价结果。

表3　定性因素的隶属度取值

1.2.5进行模糊推论，求解模糊关系方程

B=(b1,b2,b3)=A·R

(1)

式中：B——评价单元煤矿采空区稳定性综合评价结果矩阵；b1,b2,b3——隶属于较不稳定、不稳定、极不稳定的隶属度； A——评价因子的权值矩阵； R——模糊关系矩阵。

2实例计算

以山西省晋城市凤凰山矿凤2采空区为例，来说明煤矿采空区稳定性Ⅲ级模糊层次分析步骤与评价结果。

2.1　矿区简介

凤凰山矿位于晋城市泽州县境内，东西长为4.3 km，南北长为7.5 km，面积29.34 km2。地表呈现为侵蚀的低山丘陵地貌，除西部发育白马寺逆断层外，主要发育一系列落差小于5 m的小断层，以正断层为主，主要为沿北北东向分布规模不等的向背斜构造。含水层为第四系砂砾孔隙含水层组和二叠系砂岩裂隙含水层组。3#煤层平均涌水量为2 260 m3/d；9#煤层平均涌水量为2 535 m3/d；15#煤层平均涌水量为2 559 m3/d。

区内多为第四系黄土覆盖，基岩出露面积约为井田面积的25%，主要分布于中部的山梁及沟壑地段，大部分为下石盒子组及下石盒子组中、下部地层，井田内的含煤地层分别为上石炭统太原组(C3t)和下二叠山西组(P2s)。研究区煤层特征见表4。

表4　研究区煤层特征

注：Ps指下二叠山西组地层； C3t指上石炭太原组地层。

凤凰山矿建矿以来，3#煤层一直为主要开采煤层，主期用炮采，后改为普采，采用全部垮落法管理顶板。20世纪80年代全部实现综采，3#煤层平均厚约6.1 m，采用分层开采方式，先采上分层，一般采高为3 m，其余为下分层，二次开采，1996年开始9#煤层先期巷道掘进工作，1998年开采9#煤层。

2.2　凤凰山矿采空区评价因子权值计算

采用层次分析法可确定各评价因子权重。依据1—9标度法，对各因子进行两两比较，综合评价，可求取各因子权重。本文以因素层为例说明层次分析法确定权重方法步骤。

2.2.1构建对比矩阵因素层的地质因素、采空因素、外部因素及时间因素分别对应A1，A2，A3及A4，参考表1，并对其进行两两对比，可建立对比矩阵：

(2)

式中：A1，A2，A3，A4——代表因素层的地质因素、采空因素、外部因素及时间因素。下同。

2.2.2计算权重系数及一致性检验计算重要性排序方法有几何平均法、算术平均法及特征向量法等[9]，本文采用特征向量法，计算的权重系数为：

(3)

判断矩阵一致性检验采用一致性比率CR，CR=CI/RI，其中CI为判断矩阵的一般一致性指标，RI为判断矩阵的平均随机一致性指标。当CR<0.1，认为判断矩阵具有满意的一致性。判断矩阵A的一致性比率为0.001 6，矩阵具有满意的一致性。

故因素层A1，A2，A3及A4权重分别为0.368 4，0.368 4，0.070 4及0.192 8。

采用相同方法可确定各因素层下要素层权重及各要素层下因子层权重，权重取值范围为[0.000 0～1.000 0]，各因素层下要素层权重之和为1.000 0，各要素层下因子层权重之和为1.000 0。权重详见表4。

2.3　凤凰山矿凤2采空区各评价因子隶属度取值的确定

凤凰山矿凤2采空区包括3#，9#及15#煤采空区。其中，3#采空区形成于1988—2003年，开采深度约150 m，煤层平均厚度约6.10 m；9#采空区形成于2001—2010年，开采深度约210 m，煤层平均厚度约1.40 m；15#采空区形成于2010—2011年，开采深度约250 m，煤层平均厚度约2.30 m。其中，3#采空区为主要采空区，各煤层均采用长壁式采煤法。

结合晋城市及周边地区煤矿采空区特点，充分考虑该区地质、采掘技术、采空时间及宏观变形特征等各影响因子特点及发育规律，依据模糊综合评价隶属度确定方法，可综合确定各因子隶属度(表5)。

2.4　凤凰山矿采空区稳定性综合评价

(1) Ⅰ级模糊综合评价：

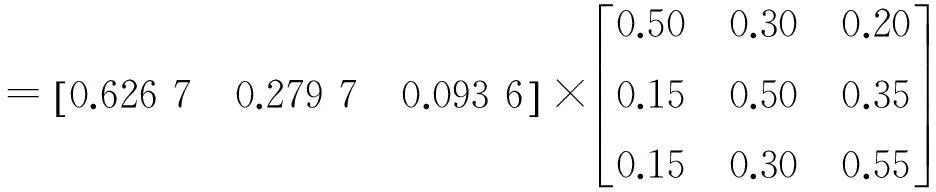
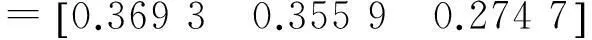
(2) Ⅱ级模糊综合评价：

(3) Ⅲ级模糊综合评价：

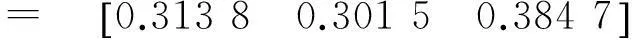
表5　凤凰山矿采空区稳定性评价因子权值分配及隶属度取值

因素层(权重要素层(权重因子层(权重隶属度地质因素(0.3684)煤层埋藏几何条件(0.4845)地层(0.6267)[0.50,0.30,0.20]埋藏深度(0.2797)[0.15,0.50,0.35]松散层厚度(0.0936)[0.15,0.30,0.55]地质构造(0.2967)褶皱程度(0.4444)[0.25,0.55,0.50]断层密度(0.4444)[0.25,0.55,0.50]节理裂隙程度(0.1112)[0.30,0.40,0.30]岩石物理力学性质(0.1094)软硬岩厚度比(0.6738)[0.30,0.50,0.20]顶板岩性(0.2255)[0.40,0.30,0.30]顶板厚度(0.1007)[0.30,0.40,0.30]水文地质特征(0.1094)含水层充水(0.7258)[0.30,0.40,0.30]水解、软化(0.1020)[0.50,0.30,0.20]地下水运动(0.1721)[0.50,0.30,0.20]采空因素(0.3684)采空区几何条件(0.8333)采煤层数(0.0899)[0.10,0.30,0.60]开采厚度(0.2897)[0.10,0.25,0.65]深厚比(0.5002)[0.15,0.25,0.60]走向长度(0.1202)[0.30,0.40,0.30]采掘技术(0.1667)开采方法(0.4934)[0.10,0.30,0.60]顶板管理方法(0.3108)[0.20,0.20,0.60]重复采动情况(0.1958)[0.10,0.40,0.50]外部因素(0.0704)地表宏观变形迹象(1.0000)塌陷(0.6028)[0.20,0.50,0.30]地裂缝(0.3972)[0.10,0.40,0.50]时间因素(0.1928)时间(1.0000)采空年限(1.0000)[0.50,0.20,0.30]

2.5　采空区稳定性综合评价结果

向量[0.313 8,0.301 5,0.384 7]即为凤2采空区的模糊层次分析法评价结果，根据隶属度最大化原则，凤2采空区稳定性级别属极不稳定区。据现场调查，凤2采空区地表塌陷及地裂缝分布严重，总体属于极不稳定区，现场调查与模糊层次分析法评价结果相一致。

3结 论

(1) 将影响煤矿采空区稳定性的因素分为4大因素，8大要素及22个因子，各因子对煤矿采空区稳定影响程度不同，以此为基础，建立煤矿采空区稳定性评价的模糊层次分析模型。

(2) 采用层次分析法(AHP)，各因子进行两两对比，构建对比矩阵，确定各因子、各要素及各因素权重。

(3) 以凤凰山矿区凤2采空区为例，说明煤矿采空区稳定性Ⅲ级模糊综合评判过程，评价结果显示：该采空区稳定性级别属于极不稳定，评价结果与实际情况基本一致。

[参考文献]

[1]邓喀中,谭志祥,张宏贞,等.长壁老采空区残余沉降计算方法研究[J].煤炭学报,2012,37(10):1601-1605.

[2]沈明荣,陈建峰.岩体力学[M].上海：同济大学出版社,2006.

[3]《工程地质手册》编委会.工程地质手册[M].北京：中国建筑工业出版社,2007.

[4]滕永海,张俊英.老采空区地基稳定性评价[J].煤炭学报,1997,22(5):504-508.

[5]谢和平,周宏伟,王金安,等.FLAC在煤矿开采沉陷预测中的应用及对比分析[J].岩石力学与工程学报,1999,18(4):397-401.

[6]王生俊,贾学民,韩文峰,等.高速公路下伏采空区剩余沉降量FLAC3D计算方法[J].岩石力学与工程学报,2005,24(19):3545-3550.

[7]高速公路采空区(空洞)勘察设计与施工治理手册[M].北京：人民交通出版社,2005.

[8]Satty T L. How to make a decision: The analytic hierarchy process[J]. European Journal of Operational Research, 1990,48(1):9-26.

[8]王念秦,罗东海.滑坡发育阶段判定的改进可拓层次分析方法[J].中国地质灾害与防治学报,2009,19(4):27-32.

[9]邓雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,24(7):93-100.

[10]常建娥,蒋太立.层次分析法确定权重的研究[J].武汉理工大学学报:信息与管理工程版,2007,29(1):153-156.

[11]李世勇.工程模糊数学及应用[M].哈尔滨:哈尔滨工业大学出版社,2004:99-101.

Application of Fuzzy Evaluation Method in Stability Evaluation of Mined-out Area

LUO Donghai

(ARSCGeologicalExplorationInstitute,ChinaNationalAdministrationofCoalGeology,Xi’an,Shaanxi710054,China)

Abstract：[Objective] To analyze the feasibility of fuzzy evaluation method in stability evaluation of mined-out area.[Methods] We divided the driving factors of the stability of mined-out area into four classes: geological factors, mined-out factors, external factors and time factor; divided the secondary factors into eight elements, including buried characteristics of coal seam, tectonic characteristics, physical and mechanical properties of the overlying strata, hydrogeology feature, refine formation, buried depth of coal seams, thickness of loose layer, and so on; divided the stability of mined-out area into three grades: less stability, instability and extremely instability. We used fuzzy analytic hierarchy process to establish evaluation stability model, and to construct the comparison matrix. We took Fenghuangshan mine area as a case study to evaluate the stability.[Results] The study area was found to be extremely instable, and the result is consistent with the site investigation.[Conclusion] Fuzzy evaluation method is feasible and can be applied to other mined-out areas. It can also provide guides to mine areas for rational planning and mine exploitation, having practical value.

Keywords:mined-out area; stability evaluation; fuzzy evaluation method; model

文献标识码：B

文章编号：1000-288X(2015)01-0176-05

中图分类号：TD327

收稿日期：2013-11-12修回日期：2014-01-24

第一作者：罗东海(1985—)，男(汉族),福建省宁化县人,硕士,工程师,主要从事工程地质方面的研究。E-mail:luodonghai2003@163.com。