考虑降损和平抑峰谷的配电网储能电池Pareto优化模型

熊超,马瑞

(长沙理工大学电气与信息工程学院，长沙市 410004)



考虑降损和平抑峰谷的配电网储能电池Pareto优化模型

熊超,马瑞

(长沙理工大学电气与信息工程学院，长沙市 410004)

为发挥储能电池在配电网运行中降损及平抑峰谷的作用，建立了一种考虑降损和平抑峰谷的配电网储能电池Pareto多目标优化模型。该模型以配电系统中有功损耗最小和1天中各时段负荷方差最小为目标函数，以储能电池的充放电功率为控制变量，以罚函数的形式处理电池容量约束和静态安全约束。依据日负荷曲线获取储能电池最佳充放电时段，结合前推回代潮流计算方法和带精英策略的快速非支配排序遗传算法(non-dominated sorting genetic algorithm II，NSGA-II)对多目标模型进行求解。基于最大满意度，在Pareto解集中分别分析了网损最小、削峰填谷效果最优和网损与削峰填谷折中最优3种优化方案，以获取不同的储能电池运行优化方案。最后，以IEEE33配电网系统为例，验证了所提方法的实用性和有效性，并分析了不同决策策略下运行方案的优劣，为配电网经济运行提供决策参考。

储能电池；削峰填谷；网损；运行优化；Pareto

0 引 言

随着我国城市化进程不断加速，用电负荷不断升高，城市配电网的昼夜峰谷差逐步增大。仅依靠原有的发电侧有功功率调节方法已难以满足配电网安全经济运行要求。伴随现代电力技术与材料科学的日益成熟，储能电池技术已逐渐成为电网有功功率调节的重要方法。其不仅可以有效地实现需求侧管理，削减昼夜间负荷峰谷差，还能提高电力设备利用率与经济效益[1-5]。如何有效控制储能电池的充放电行为，以满足配电网运行的不同需求，已成为关注的热点。

目前，针对储能电池系统的优化运行主要从以下2个方面进行分析。一方面通过优化储能电池充放电时段和电量，对负荷进行优化，提高负荷管理能力。这类研究根据储能电池工作模式可分为负荷转移模式[6-8]和套利模式[9-12]。文献[7]引入充放电次数限制和放电深度限制等非连续约束条件，将电池电量离散化，解决了含有非连续约束的优化问题。文献[8]运用负荷预测与动态规划方法，进行实时优化。文献[9-11]运用储能电池对负荷进行合理优化，使用户和电网获得最大收益。另一方面将储能电池与分布式能源相互配合，平抑出力波动，增加能源利用率，使微电网取得最大的运行效益。文献[13]建立了不同的优化运行目标，并对不同目标的经济性进行了对比分析。文献[14]在目标函数中加入蓄电池放电罚函数，对微电网进行实时能量优化调度。文献[15]考虑能源不确定性与负荷不确定性所带来的波动，建立了动态优化模型。文献[16]以经济效益最优、可靠性最好、可再生能源功率波动最小、可再生能源发电计划最符合作为储能电池优化目标，提高微电网的经济性与可靠性。上述相关研究主要集中在微电网领域，对配电网的相关领域研究较少，或主要以削峰填谷作为主要优化目标。然而，配电网线损是表征电力系统经济运行的一项重要技术经济指标。且负荷曲线平滑到一定程度时，配网中的网损电量可能会出现增加的现象，导致配电网运行的经济性下降[17]。因而网损也是储能电池运行优化中需考虑的一项重要因素。文献[17]综合考虑网损与削峰填谷，建立了电池储能站优化运行模型。但其主要是通过选择权重，将多目标函数转成单目标函数，来求得最优解。故其优化结果受主观影响较大，且每次优化只能得到一种权重值下的结果，而非一组直观的可供偏好选择的决策方案，不能客观分析网损与削峰填谷之间的辩证关系。

基于上述分析，本文针对配电网中储能电池运行对负荷曲线和网损变化的影响，以网损最小和削峰填谷效果最好为目标构建储能电池双目标优化运行模型。模型以储能电池的充放电功率作为控制变量，并将储能电池容量越限与节点电压越限作为罚函数计及其中。首先，在已知的日负荷曲线基础上优化得到储能电池充放电时段。其次，采用带精英策略的快速非支配排序遗传算法(non-dominated sorting genetic algorithm II，NSGA-II)对储能电池运行优化模型进行求解，获得Pareto最优解集。最后，采用不同的决策方式，获取单目标极端优化解与多目标最优折衷解，并对其进行对比分析。使电网运行人员可以依据不同需求，选取合理的运行策略。

1 储能电池运行优化模型

1.1 目标函数

(1)网损优化。

根据辐射型配电网的特点，利用前推回代法逐条计算线路损耗。在T时间段内的总网损为

(1)

式中：N为配电网中总支路数；Pl,Loss(t)为线路l在t时段的网损。

(2) 削峰填谷。

本文采用负荷方差作为目标函数，来表达削峰填谷效果。将1天划为T个时段，求解总体最小负荷方差。其表达式如下：

(2)

(3)

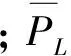
(3)综合目标函数。

储能电池充放电量与上一状态的储能电池剩余容量、该状态电池充放电情况有关。为体现储能电池在时序上的连续性以及实现系统潮流约束，在目标函数中加入罚函数fpunish，以实现这类表征系统运行状态的约束[18]。该综合目标函数表达式为

Fi(x,u)=fi(x,u)+fpunish

(4)

式中fi(x,u)为第i个原始目标函数，x和u分别表示状态变量与决策变量。

罚函数主要由2部分构成：第1部分为节点电压越限惩罚项；第2部分为储能电池充放电量越限惩罚项，以保证t段储能电池充放电量不超过储能电池上一时段的剩余容量。

(5)

式中：T为储能电池充放电的总时段数；λU为电压越限罚因子;N1为配网中的节点数；ΔUa(t)为对应节点电压越限值；UMax和UMin分别表示节点电压的上下限；λS为储能电池充放电量越限罚因子；N2为所配置的储能电池数；ΔSb(t)为对应节点储能电池充放电量越限值；SMax和SMin分别表示储能电池容量的上下限。

(6)

(7)

式中：Ua(t)为t时段节点a的电压；Sb(t)为t时段第b个储能电池的剩余容量。

1.2 约束条件

(1)储能电池容量约束。

SMin≤S(t)≤SMax，t=0,1,2,…，N

(8)

式中:SMax和SMin分别为储能电池容量的上下限；S(t)为t时段储能电池的存储电量。

S(m)=Sinitial

(9)

S(t)=S(t-1)+PB(t)×Δt,t=m,m+1,…,N

(10)

S(N)=Sfinal

(11)

式中:Sinitial和Sfinal分别为储能电池储存电量的初始值与最终值；PB(t)为t时段储能电池的充放电功率。

(2)储能电池充放电状态约束。

因储能电池在t时段的剩余容量与上一时段的充放电量相关，所以t时段储能电池存储电量为上一时段的电池储存电量与该时段的充放电功率的叠加，不应超过储能电池容量上下限。采用罚函数处理如1.1节所述。

(3)储能电池充放电功率约束。

-PMax≤PB(t)≤PMax

(12)

储能电池在各个时段的充放电功率不能超过其功率的上下限。

(4)节点电压约束。

UMin≤U(t)≤UMax

(13)

式中：U(t)为t时段各节点的节点电压；UMax和UMin分别为节点电压的上下限，采用罚函数处理，如1.1节所述。

2 储能电池运行优化流程

2.1 储能电池充放电时间优化

储能电池充放电时段的确定，是储能电池系统进行运行优化的基础。本文基于已知固定日负荷曲线，采用文献[2]中的实用简化求解算法，可优化得到储能电池在该日负荷曲线下的最优充放电时间段。总的充电时间段数与总的放电时间段数相等，即

(14)

2.2 储能电池充放电功率优化

与单目标优化相比，多目标优化的解并不唯一，而是存在一个Pareto最优解集。其各目标间通过储能电池的控制变量相互制约，且一个目标最优时必然牺牲另一个目标的性能。针对上述问题，基于上节优化得到的储能电池充放电时间段，运用NSGA-II算法对各时段储能电池充放电功率进行多目标优化，得到Pareto前沿及最优解集。其流程如图1所示。

图1 储能电池优化运行流程

2.3 最优折衷解决策

求出Pareto最优解集后，利用最大满意度求解最优折衷解。首先运用模糊隶属度函数来求解每个解中的各目标函数的满意度。因本文的目标函数为削峰填谷与网损，所优化的目的是使网损电量尽可能减小与负荷曲线更平滑，故两目标均选取偏小型模糊满意度函数求解。再采用式(15)求解Pareto解集中每个解所对应的标准化满意度，标准化满意度值最大的解为最优折衷解。第k个解的标准化满意度计算与第k个解中各目标函数的偏小型模糊满意度[19]计算分别如下：

(15)

(16)

3 算例分析

本文选取IEEE33节点配电网系统进行仿真研究，结构如图2所示，假定在节点7、17、24、31上分别配置等容量储能电池。系统预测负荷采用固定日负荷曲线。已知储能电池PMax=120 kW，电池容量S=750 kW·h，UMax=1.10 pu，UMin=0.95 pu，SMin=0，SMax=S。假设1天中储能电池开始充电时，其电池电量Sinitial=0,优化周期设为1天，分为24个时段，经过1个优化周期之后，储能电池剩余电量Sfinal=0。

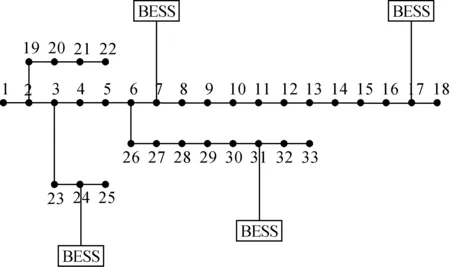
图2 IEEE33节点配电网

3.1 储能电池充放电时间优化结果

根据预测得到的配电网日负荷曲线，如图3所示。利用实用简化求解算法求得储能电池充电时段为01∶00—06∶00，放电时段为11∶00—13∶00、17∶00—19∶00。

图3 日负荷曲线

3.2 储能电池充放电功率优化结果

基于上述充放电优化时段，首先利用NSGA-II算法对储能电池在充放电时间段内的充放电功率进行优化，得到一组Pareto优化解集。图4、5分别为充电阶段与放电阶段优化所得到的Pareto前沿。然后对这组优化结果分别选取负荷方差最小、网损最小与优化折衷解等方案，对比分析各最优解中储能电池充放电优化结果对系统运行优化目标的影响。图6为不同优化方案下削峰填谷效果的对比，表1为不同目标下的系统网损值。由图6和表1可知，在充电阶段所增加的负荷越大，其负荷曲线的整体削峰填谷效果越佳；在充电阶段所增加的负荷越小，其减小的网损电量越大。

图4 放电优化Pareto图

图5 充电优化Pareto图

图6 不同优化目标下日负荷曲线

kW

(1)削峰填谷最优方案。图7为选取削峰填谷最优方案时，平抑峰谷的效果及1个调度周期内储能电池的充放电量。其在充电时段储能电池所转移的负荷为1.831 MW，在放电阶段所转移的负荷为2.37 MW。在1个调度周期内其所转移的负荷比为5.7%，远超过其他2个方案所转移的负荷。

图7 削峰填谷最优下日负荷与优化前日负荷对比

表2为削峰填谷前后网损对比结果，由表2和表1可知，在充电阶段，系统的整体网损增加0.096 MW，而在放电阶段，系统的整体网损会减小0.194 MW。但为了使削峰填谷效果更佳，本方案在充电阶段所增加的网损，比其他2个方案多，而在放电阶段所减小的网损小于其他2个方案，故其所减小的总网损电量最小。

表2 削峰填谷前后网损对比

Table 2 Network losses before and after load shifting

kW

(2)网损电量最优方案。图8为选取网损电量最优方案时，平抑峰谷的效果及1个调度周期内储能电池的充放电量。其在充电时段储能电池所转移的负荷为1.46 MW，小于其他2个方案中的转移负荷。在放电阶段所转移的负荷为2.365 MW，在3个方案中大于折中方案转移的负荷，小于削峰填谷最优时转移的负荷。在1个调度周期内其所转移的负荷比为5.2%。

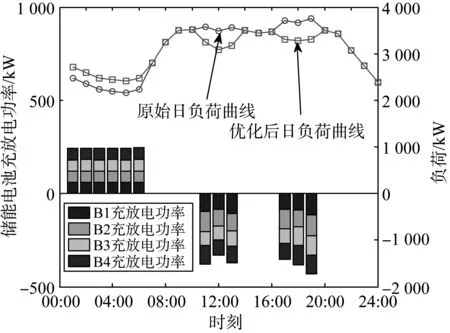
图8 网损最优下日负荷与优化前日负荷对比

表3为网损电量目标最小时网损对比结果，由表3和表1可知，在充电阶段，系统的整体网损增加0.071 MW，而在放电阶段，系统的整体网损会减小0.215 MW。其在放电时所降低的网损远大于充电时所增加的网损，以达到降损的效果。因一个目标最优时，必将影响另一个目标的性能。故本方案削峰填谷效果受到网损电量的影响较大。

表3 网损电量目标最小时网损对比

Table 3 Network losses comparison with

minimum network loss objective

kW

(3)优化折衷解方案。图9为选取优化折衷解方案时，平抑峰谷的效果及1个调度周期内储能电池的充放电量。其在充电时段储能电池所转移的负荷为1.518 MW，在3个方案中大于网损最小时转移的负荷，小于削峰填谷最优时转移的负荷。在放电阶段所转移的负荷为2.269 MW，小于其他2个方案中的转移负荷。在1个调度周期内其所转移的负荷比率为5.1%。

图9 优化折衷解日负荷与优化前日负荷对比

表4为折衷解的网损对比结果，由表4和表1可知，在充电阶段，系统整体网损增加0.069 MW，低于其他2个方案所增加的网损。而在放电阶段，系统的整体网损减小0.181 MW，低于其他2个方案所减小的网损。虽在放电阶段所减小的网损小于削峰填谷方案，但在充电阶段所增加的网损远小于削峰填谷最优方案，故该方案减小的总网损还是大于削峰填谷最优方案。

表4 折衷解的网损对比

Table 4 Network losses comparison of compromise solution

kW

4 结 论

(1)当配电网的负荷峰谷差较大时，投入储能电池不仅可以削峰填谷，也能达到降损效果。但削峰填谷效果与降损效果并不存在线性相关的关系，即削峰填谷效果最佳时并不是降损效果最好时。

(2)削峰填谷效果最佳时，要求储能电池充电阶段与放电阶段所转移的负荷尽可能最大。而降损效果的好坏主要与放电阶段储能电池放电量相关。

(3)优化折衷解辩证地考虑了负荷曲线平坦度与降损2个方面，避免了传统多目标问题求解方法对优化结果的主观影响，使电网依据实际需求，科学合理调度储能电池运行功率，达到配电网经济运行的目的。

[1]王承民，孙伟卿，衣涛，等.智能电网中储能技术应用规划及其效益评估方法综述[J].中国电机工程学报，2013，33(7)：33-41.Wang Chengmin，Sun Weiqing，Yi Tao， et al.Review on energy storage application planning and benefit evaluation methods in smart grid[J].Proceedings of the CSEE，2013,33(7)33-41.

[2]周峰,王科,朱桂萍,等.微电网孤岛模式下全钒液流电池逆变器控制[J] .中国电力,2011,44(3):81-85.Zhou Feng,Wang Ke,Zhu Guiping, et al.Control strategy for vanadium redox battery inverter in islanding microgrid[J] .Electric Power,2011,44(3):81-85.

[3]刘向向,王奔,张翔,等.基于钒电池储能系统的风电场并网功率平抑控制[J] .中国电力,2013,46(8):48-53.Liu Xiangxiang , Wang Ben , Zhang Xiang , et al.Smoothing Control of Grid-Connected Wind Power by VRB-Based Energy Storage Systems[J] .Electric Power,2013,46(8):48-53.

[4]靳文涛,李建林.电池储能系统用于风电功率部分“削峰填谷”控制及容量配置[J] .中国电力,2013,46(8):16-21.Jin Wentao , Li Jianlin.BESS for Wind Power “Peak Shaving” Control and Capacity Configuration[J] .Electric Power,2013,46(8):16-21.

[5]金一丁,宋强,陈晋辉,等.大容量电池储能电网接入系统[J] .中国电力,2010,43(2)：16-20.Jin Yiding,Song Qiang,Chen Jinhui, et al.Power conversion system of large scaled battery energy storage[J] .Electric Power,2010,43(2):16-20.

[6]陈满，陆志刚，刘怡，等.电池储能系统恒功率削峰填谷优化策略研究[J].电网技术，2012，36(9):232-237.Chen Man，Lu Zhigang，Liu Yi， et al.Research on optimal peak load shifting strategy of battery energy storage system operated in constant power mode[J].Power System Technology，2012，36(9):232-237.

[7]鲍冠南，陆超，袁志昌，等.基于动态规划的电池储能系统削峰填谷实时优化[J].电力系统自动化，2012，36(12):11-16.Bao Guannan，Lu Chao，Yuan Zhichang， et al.Load shift real-time optimization strategy of battery energy storage system based on dynamic programming[J].Automation of Electric Power Systems，2012，36(12):11-16.

[8]Bao G N，Lu C，Yuan Z C, et al.Battery energy storage system load shifting control based on real time load forecast and dynamic programming[C]//8th IEEE International Conference on Automation Science and Engineering.Seoul: IEEE, 2012：815-820.

[9]Zhang T，Cialdea S，Orr J A， et al.Outage avoidance and amelioration using battery energy storage systems[C]//Power Systems Conference (PSC).Clemson, SC: IEEE, 2014：1-6.

[10]Zhang T，Cialdea S，Alexander E， et al.Electric energy cost reduction by shifting energy purchases from on-peak tmes purchases from on-peak times[C]//Electrical Power & Energy Conference (EPEC).Halifax, NS：IEEE，2013：1-5.

[11]刘天琪，江东林.基于储能单元运行方式优化的微电网经济运行[J].电网技术，2012，36(1)：45-50.Liu Tianqi，Jiang Donglin.Economic operation of microgrid based on operation mode optimization of energy storage unit[J] .Power System Technology，2012，36(1)：45-50.

[12]Hu Z C，Zhang S，Zhang F，et al.SCUC with battery energy storage system for peak-load shaving and reserve support[C]//Power and Energy Society General Meeting.Vancouver，BC：IEEE，2013：1-5.

[13]丁明，张颖媛，茆美琴，等.包含钠硫电池储能的微网系统经济运行优化[J].中国电机工程学报，2011，31(4)：7-14.Ding Ming， Zhang Yingyuan， Mao Meiqin， et al.Economic operation optimization for microgrids including Na/S battery storage[J] .Proceedings of the CSEE，2011，31(4)：7-14.

[14]石庆均，江全元.包含蓄电池储能的微网实时能量优化调度[J].电力自动化设备，2013，33(5)：76-82.Shi Qingjun， Jiang Quanyuan.Real-time optimal energy dispatch for microgrid with battery storage[J].Electric Power Automation Equipment，2013，33(5)：76-82.

[15]丁明，徐宁舟，毕锐.负荷侧新型电池储能电站动态功能的研究[J].电力自动化设备，2011，31(5)：1-7.Ding Ming，Xu Ningzhou，Bi Rui.Dynamic model of new-type battery energy storage system at demand side[J].Electric Power Automation Equipment，2011，31(5)：1-7.

[16]钟宇峰，黄民翔，叶承晋，等.基于电池储能系统动态调度的微电网多目标运行优化[J] .电力自动化设备，2014，34(6)：114-121.

Zhong Yufeng，Huang Minxiang，Ye Chengjin， et al.Multi-objective optimization of microgrid operation based on dynamic dispatch of battery energy storage system[J].Electric Power Automation Equipment，2014，34(6)：114-121.

[17]章美丹，宋晓喆，辛焕海，等.计及网损的配电网电池储能站优化运行策略[J].电网技术，2013，37(8)：2123-2128.Zhang Meidan， Song Xiaozhe， Xin Huanhai，et al.Optimal operation strategy of battery energy storage system in distribution networks with consideration of power losses[J].Power System Technology，2013，37(8)：2123-2128.

[18]谢开贵，肖畅.计及负荷不确定性的无功优化模型与算法[J].电力系统保护与控制，2011，39(4)：18-22..Xie Kaigui，Xiao Chan.A reactive power optimization model and algorithm considering load uncertainty[J].Power System Protection and Control，2011，39(4):18-22.

[19]Farina M，Amato P.A fuzzy definition of “optimality” for many-criteria optimization problem[J].IEEE Transactions on System，Man and Cybernetics：Part A，2004，34(3)：315：326.

(编辑：张小飞)

A Pareto Optimal Model for Energy Storage Battery in Distribution Network Considering Network Loss and Peak-Valley Difference Alleviation

XIONG Chao，MA Rui

(School of Electrical & Information Engineering, Changsha University of Science & Technology, Changsha 410004, China)

To make better use of energy storage battery’s role in reducing network loss and alleviating peak-valley difference, a Pareto multi-objective optimization model was proposed for energy storage battery in distribution network with considering network loss reduction and peak-valley difference alleviation, which took the minimum network power loss in distribution system and the minimum variance between load of every period and the average value as objective functions, the charge/discharge power of storage battery as control variables, and transformed the constraints on battery capacity and static security into penalty function.According to daily load curve, the optimal charge and discharge periods of energy storage battery were obtained.Combined with forward-backward sweep calculation method, fast non-dominated sorting genetic algorithm II (NSGA-II) with elitist strategy was adopted to solve the multi-objective model.Based on satisfaction-maximizing method, this paper analyzed three optimization schemes in Pareto solution set: the minimum network loss, the best load shifting effect and the compromise solution between two objectives, in order to obtain different optimization schemes of energy storage battery.Finally, taking IEEE33 distribution system as example, this paper proved the validity and feasibility of the proposed method, and analyzed the advantages and disadvantages of operation schemes under different decision strategies, which could provide decision-making reference for the economic operation decision of distribution networks.

energy storage battery; load shift; network losses; operation optimization; Pareto

国家自然科学基金项目(51277015)。

TM 912

A

1000-7229(2015)08-0034-07

10.3969/j.issn.1000-7229.2015.08.006

2015-04-25

2015-05-29

熊超(1989)，男，硕士研究生，研究方向为电力系统分析与控制；

马瑞(1971)，男，博士，教授，研究方向为风电并网分析与控制，电压稳定、电力系统分析与控制和电力市场。

Project Supported by National Natural Science Foundation of China (51277015).