支座偏心距对匝道桥抗倾覆稳定性能的影响

王　伟，王庆忠

(1.济南西城投资开发集团有限公司，山东　济南　250117；2.济南西城投资开发集团有限公司，山东　济南　250117)



支座偏心距对匝道桥抗倾覆稳定性能的影响

王伟1，王庆忠2

(1.济南西城投资开发集团有限公司，山东济南250117；2.济南西城投资开发集团有限公司，山东济南250117)

王伟(1988—)，助理工程师，硕士研究生，主要从事土木工程行业工作；

王庆忠(1970—)，高级工程师，主要从事土木工程行业工作。

摘要：文章以现运营的某一匝道桥为例，从桥梁支座偏心距的布置出发，结合现有的公路桥梁规范，建立MIDAS/CIVEL有限元模型对匝道桥的抗倾覆稳定性能进行计算分析，探讨支座偏心距对匝道桥整体抗倾覆稳定性能的影响，并提出支座合理化设计的相关建议，为类似工程的设计计算提供参考。

关键词：匝道桥；支座偏心距；抗倾覆稳定性；MIDAS/CIVEL；合理设计

0引言

匝道桥在城市高架立交中运用较为广泛，为了节约桥下空间，提高美观效果，设计者经常采用独柱墩形式。城市匝道较主线桥梁往往自重小、宽度窄，移动荷载所占比重较大，随着交通量日益增多，桥梁所承受的荷载日益增大，近几年也频频发生桥梁倾覆事故。在匝道桥的设计过程中，如何安排合理的偏心距对其抗倾覆性能极为重要，因此有必要对此类匝道桥的设计进行必要的抗倾覆稳定性能验算，得到最合理的支座偏心距。

1工程概况

该十字路跨线桥采用等高度连续梁，梁高1.4 m，4跨一联，全桥三联。布置为：(4×20+4×30+4×20)m。主梁为等高度箱梁，单箱单室，高1.4 m，顶板宽8.0 m，底板宽4.5 m，每侧挑臂长1.75 m。跳臂端部厚15 cm，根部厚40 cm，顶板等厚25 cm，底板等厚20 cm。30 m跨径箱梁腹板厚60 cm，20 m跨径箱梁腹板厚50 cm。腹板与顶板相接处设100×20 cm承托，与底板相接处设50 cm×20 cm加腋。梁体采用C50混凝土，φj15.2钢绞线，Ryb=1 860MPa(符合GB5224-85)，荷载等级为公路1级，钢筋混凝土重力密度按25.5kN/m3取。

本论文只研究中间主梁部分，中间3个墩为独柱墩，上设盆式橡胶支座。中间的支座为固定支座，另两个为单向活动支座。两侧采用盆式橡胶支座。桥梁具体支座布置见图1(平面图)。

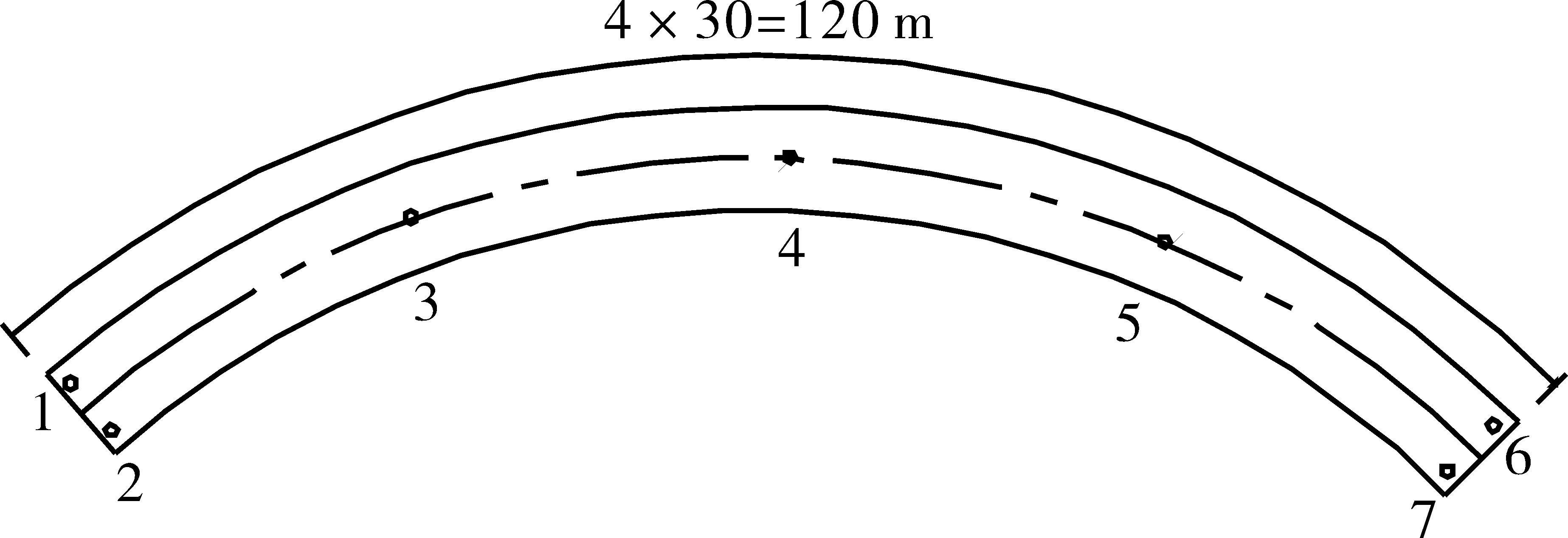
图1　支座布置图

2计算依据

根据JTGD62-2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》5.1条，抗倾覆稳定性验算应该按照极限承载力计算，荷载组合系数则按照规范4.1.6条对承载能力极限状态基本组合荷载效应系数进行取值[1]。

3建立模型

实体桥为预应力箱型梁结构体系，宜采用大型有限元软件MIDAS/CIVEL建立模型进行计算，全桥共划分为122个单元，137个节点，比较真实地模拟了主桥各梁段的截面形状，对截面变化复杂的梁段如变截面和支点处等都进行了细化。支座底部与桥墩顶部采用一般支承模拟，支座本身采用弹性连接模拟，支座顶部与主梁梁体采用刚性连接进行模拟，对于纵坡较大的桥梁，固定端模拟支座应设置在纵坡低端，这样模拟可有利于主梁梁体受力，主梁自重可以转化为梁体压应力，就相当于施加了预应力，本文所选匝道纵坡较小，所以不予考虑。建立有限元模型见图2~3。

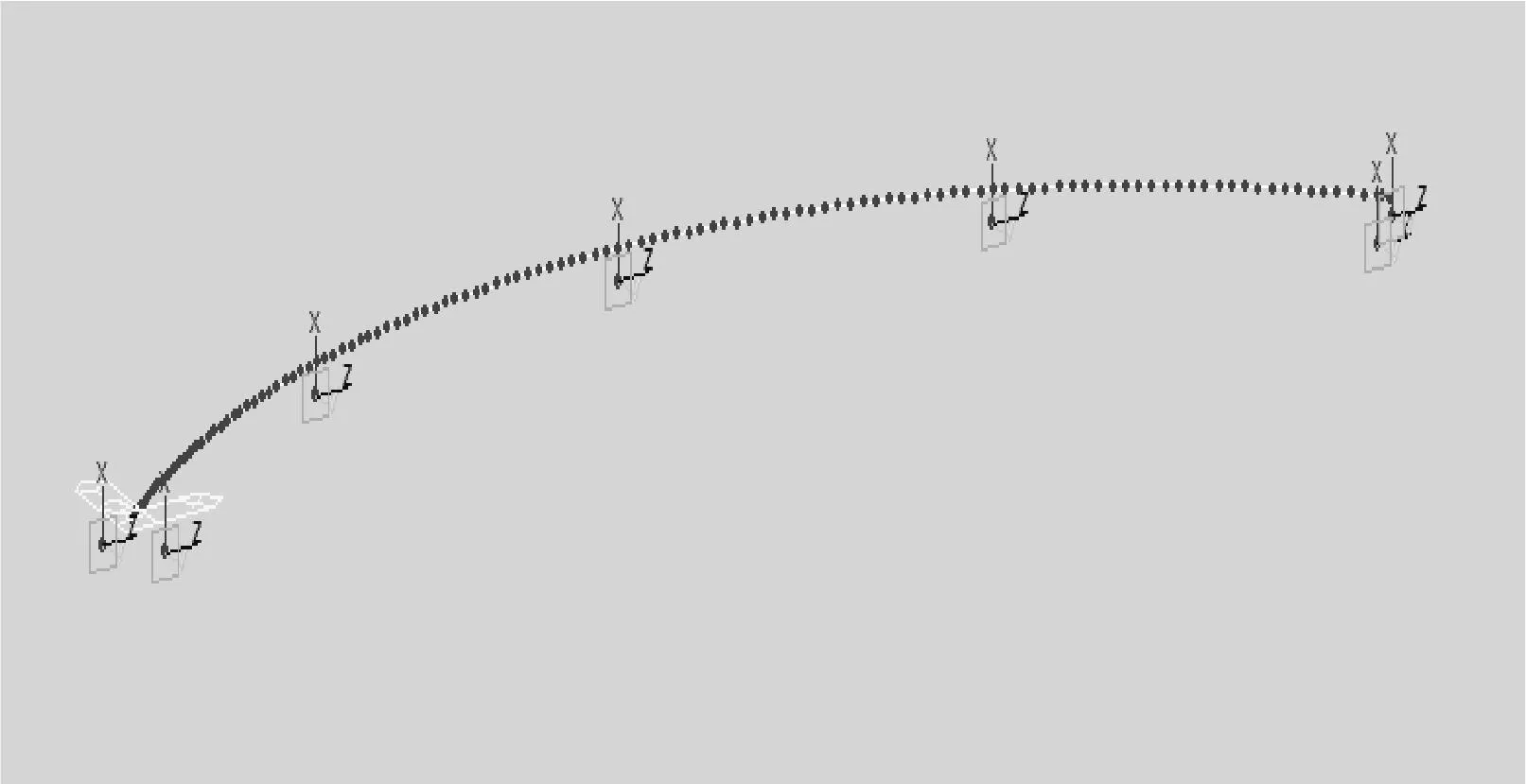
图2　支座模拟示意图

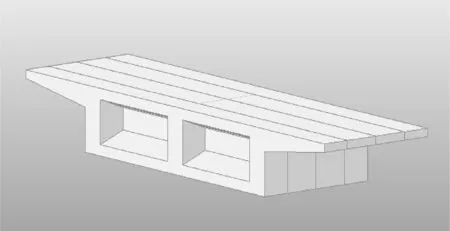
图3　变截面细部剖面图

本节计算模型所采用的工程实例依然同上，但将支座预偏心值分别设置为10cm、20cm、30cm、40cm、50cm、80cm、100cm及200cm八种情况，荷载工况为自重+二期+预应力+升温18度+移动荷载[2]。(1)计算各预偏心状态下的支座反力，并根据不同的需求，描绘曲线散点图，看其支座的受力规律，寻找出合理受力的预偏心范围；(2)通过计算分析者8种状态下梁体的扭矩及扭转位移，进一步确定合理的预偏心范围，并找到最佳预偏心值。

3.1　支座反力结果分析比较(kN)

不同预偏心下的支座反力情况见表1。

表1　不同预偏心下的支座反力表(kN)

由表1可得在预偏心值逐渐增大状态下，1#~7#支座支座反力变化图(见图4)。

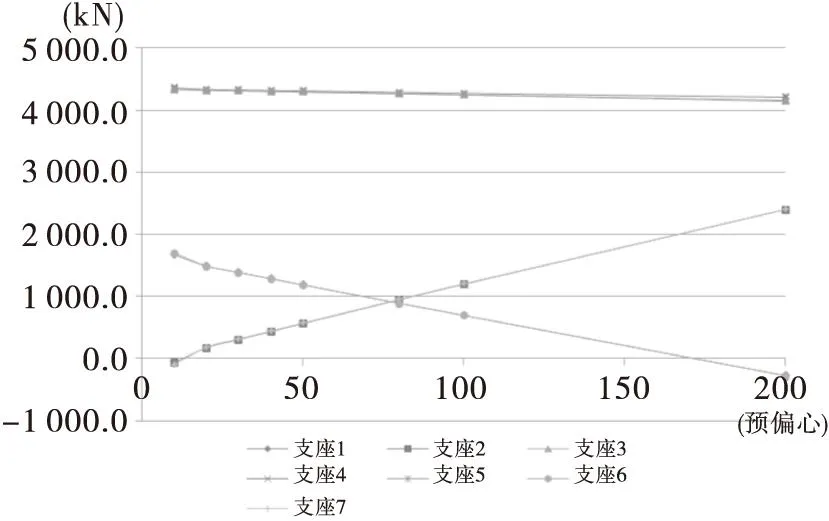
图4　各支座在不同预偏心值下的反力曲线图

由图4可发现，在预偏心值逐渐变大的过程中，3#、4#与5#支座受力基本重合，1#与6#支座受力基本重合，2#与7#支座受力基本重合。其中3#、4#与5#支座受力曲线图保持平直，这说明中间独柱墩上的单点铰支座受力与预偏心值的大小两者之间基本没什么影响；但1#与6#支座(即端部外侧支座)受力曲线随着预偏心值的增大而逐渐减小，大致在1.7m处之后将会产生负反力，此时支座将会脱空；可以看到，2#与7#支座反力在预偏心值为10cm时，都会产生负反力，此时两个支座处于脱空状态，所以此由图可以看到端支座内外侧支座不出现负反力的范围为距离梁底中心线15~175cm之间，这之间为支座预偏心合理范围。同时，单从支座反力这一点看，在预偏心值为80cm时，内外侧支座反力值相近，此时预偏心比较合理。但是支座合理预偏心不能单从支座反力或是单从单个支座受力规律来决定，还要有总体系统的对比分析[3]。

由表1可得8种预偏心状态下匝道桥支座反力曲线散点图(见图5)。

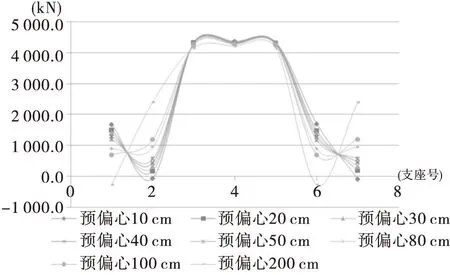
图5　不同预偏心值下的支座反力曲线图

由图5可以看到，在预偏心值为200cm时，支座反力曲线与其他预偏心下变化规律有明显的不同，这是由于偏心值过大，导致了端支座反力分布出现问题，梁体有向内侧倾覆的趋势，这是不可取的；在预偏心值为10cm时，2#、7#支座也是负反力，这些出现负反力的情况都是要避免的。在预偏心值为20~80cm范围内，受力都有相同的规律性，且都没有负反力的出现。

3.2　梁体扭矩结果分析比较

由计算模型可以得到预偏心值为10~100cm(200cm情况不予考虑)时的梁体扭矩值(见表2)。

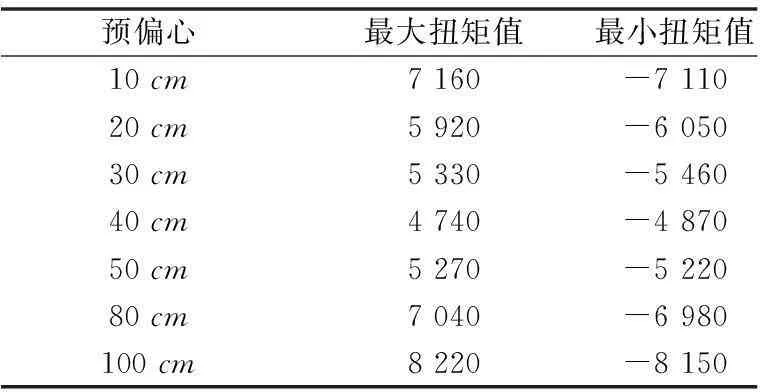
表2　不同预偏心下最大、最小扭矩值表(kN·m)

由表2可见，预偏心值在10~40cm，其端支座扭矩在逐渐减小；预偏心值为40~100cm，其端支座扭矩在逐渐增大，当偏心距为40cm时，最大、最小扭矩值在各个预偏心中是最小的，且为端部支座扭矩值。而当预偏心值在50cm、80cm、100cm时，产生的最大扭矩值位置不在端支座处，而是在独柱墩单铰支座处，由于独柱墩匝道桥抗扭效果主要是其端部支座来提供，而单铰支座不具备抗扭性能，所以这种状况是不合理的。

3.3　梁体扭转位移结果分析比较

通过模型分别计算在10~100cm(忽略200cm)的预偏心下匝道桥的扭转变形值，并绘出各状态下的扭转变形散点曲线图(见图6)。

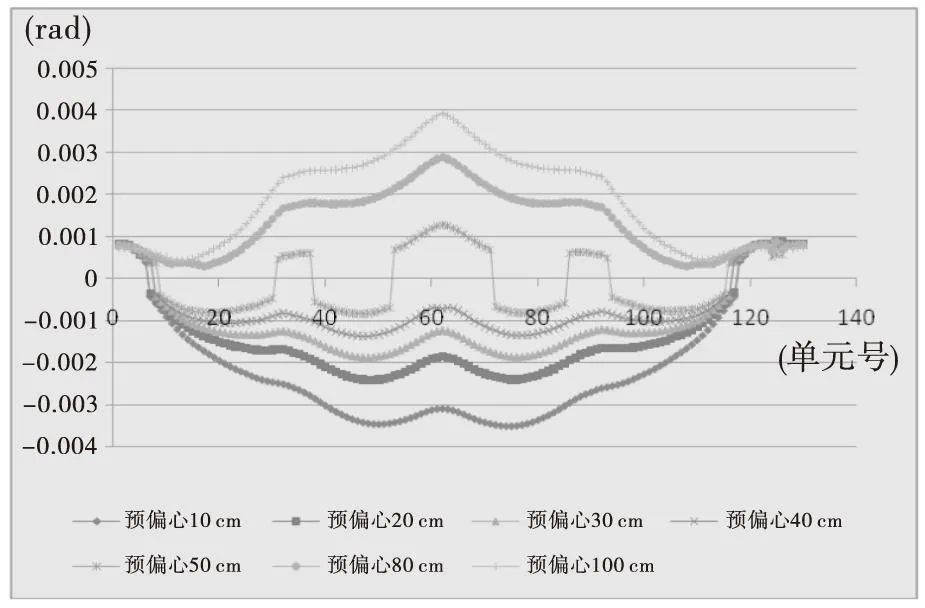
图6　不同预偏心下梁体扭转位移曲线图

由图6可以看到，预偏心值为50cm的扭转变形为一个分界点；当预偏心值>50cm时，扭转变形为正值，且随着预偏心的增大，扭转变形逐渐增大，此时，匝道桥会出现向内侧扭转的趋势；当预偏心值<50cm时，扭转变形为负值，且随着预偏心的增大，扭转位移逐渐减小，此时，匝道桥会出现向外侧扭转的趋势，并且可以看到，在预偏心值为40cm时，扭转位移最小。

4结语

结合支座反力、梁体扭矩及梁体的扭转位移结果对比分析，可以得到，在预偏心值为40cm时，匝道桥的受力最为合理，因此40cm的预偏心值为合理的预偏心值。在计算支座预偏心时，大多在对合理预偏心的确定过程中只考虑了对支座反力的对比分析，找到能够使支座不出现负反力的区间即为合理区间，内外侧支座反力相等时的偏心位置为合理偏心位置。本文细化了对支座偏心距取值的计算分析，除了考虑支座反力，还考虑到梁体扭转因素的影响，使合理区间的取值进一步缩小，这样找出的预偏心能够进一步精确。

参考文献

[1]JTGD62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[2]JTGD60-2004，公路桥涵设计通用规范[S].

[3]刘德华，金伟良，刘斌，等.独柱墩曲线梁桥中的支座分析[J].南京理工大学学报(自然科学版)，2006(1)：113-116.

Impact of Bearing Eccentricity on Anti-overturning Stability Performance of Ramp Bridges

WANG Wei1，WANG Qing-zhong2

(1.Jinan Xicheng Investment and Development Group Co.，Ltd.，Jinan，Shandong，250117；2.Jinan Xicheng Investment and Development Group Co.，Ltd.，Jinan，Shandong，250117)

Abstract：With a ramp bridge under operation as the example，starting from the arrangement of bridge bearing eccentricity，and combined with the existing highway bridge specifications，this article built the MIDAS/CIVEL finite element model to calculate and analyze the anti-overturning stability of ramp bridge，discussed the impact of bearing eccentricity on overall anti-overturning stability performance of ramp bridges，and proposed the corresponding recommendations for the rationalization design of bearings，thereby providing the reference for the design calculations of similar projects.

Keywords：Ramp bridge；Bearing eccentricity；Anti-overturning stability；MIDAS/CIVEL；Rational design

收稿日期：2015-07-06

文章编号：1673-4874(2015)08-0068-04

中图分类号：U442

文献标识码：A

DOI：10.13282/j.cnki.wccst.2015.08.017

作者简介