软岩隧道不同断面形式衬砌结构的力学特性研究
2015-03-14胡小明周勇狄贾艳领
胡小明,周勇狄,贾艳领
(广西交通科学研究院,广西 南宁 530007)
软岩隧道不同断面形式衬砌结构的力学特性研究
胡小明,周勇狄,贾艳领
(广西交通科学研究院,广西南宁530007)
胡小明(1988—),助理工程师,主要从事桥梁与隧道工程设计及咨询工作;
周勇狄(1980—),高级工程师,博士,主要从事桥梁与隧道工程设计及科研相关工作;
贾艳领(1983—),硕士,主要从事隧道监控量测及结构稳定性方面的研究工作。
摘要:对于大断面软岩隧道,选择合理的断面形式、安全稳定的洞型是保证隧道的施工及后期运营的安全基础。文章采用荷载结构法,分别对采用直边墙和曲边墙形式时隧道衬砌结构的受力进行计算分析,得出了曲墙式衬砌的受力和抗弯均优于直墙式衬砌的结论。
关键词:软岩隧道;断面形式;直边墙;曲边墙;力学特性
0引言
20世纪90年代中后期,我国开始陆续兴建一些大断面高速公路隧道。随着交通车流量的增大,在一些线路上双车道隧道已不能满足交通量日益增大所带来的需求,于是三车道隧道和四车道隧道建设成为了首选。随着隧道开挖跨度不断增大,横断面亦愈加扁平,在同一地质条件下围岩应力集中程度必然更高,衬砌受力增大,使隧道工程建设面临更大挑战[1]。近年来,国内通过引进国外较先进的施工工艺和方法,在这方面也取得了一些进步。但大断面软弱围岩公路隧道因跨度较大,隧道围岩稳定性较差,这就使设计和施工工艺的选择上有别于一般断面形式的隧道。
针对修建大断面软岩隧道时隧道断面形式的优化问题,本文以某大断面软岩隧道为依托工程,对其采用直边墙和曲边墙两种不同断面形式的施工方案施工时隧道支护结构的受力特性进行结构计算分析。研究结果可为今后类似工程的建设提供借鉴,具有重要的工程应用价值。
1结构计算方法
隧道结构计算的任务,就是采用数学力学的方法,计算分析在隧道修筑的整个过程中(包括竣工运营)隧道围岩及衬砌的强度、刚度及稳定性,为隧道的设计和施工提供具体设计参数。
纵观近年来地下结构计算理论的发展,其先后经历了从刚体力学到弹性力学,从弹性力学到粘弹性力学、弹塑性力学以及粘、弹、塑性力学这样几个阶段[2]。弹性力学理论是19世纪后期才应用于地下结构计算中的,至今仍是地下结构计算的基本理论。地下结构的计算方法主要由荷载结构法、收敛约束法和地层结构法三种。荷载结构法,就是将地层对衬砌结构的作用看作是施加在结构上的荷载(包括主动围岩压力和被动围岩压力),来计算衬砌结构的内力和变形[3]。本文选用荷载结构法,来计算分析拱形曲墙隧道和拱形直墙隧道的衬砌结构的受力和变形。
2曲墙式隧道衬砌结构计算
2.1 计算理论
拱形曲墙隧道由拱圈、曲墙和底板(仰拱)组成。由于仰拱是在曲墙和拱圈受力之后才修建的,因而结构计算中通常不考虑仰拱的影响,将拱圈和曲墙抽象为一个支承在弹性围岩上的高拱结构。由于曲墙隧道衬砌结构受到较大的竖向压力和水平压力,所以在竖向压力的作用下,拱圈顶部将产生较明显的竖向位移,形成一个不受围岩约束的脱离区。同时,竖向荷载所引起的侧墙部分的变形,将受到侧面围岩的约束,形成一个抗力区,如图1所示。假定弹性抗力为镰刀形分布,建立的模型为墙脚弹性固定而两侧受周围约束的无铰拱[2]。
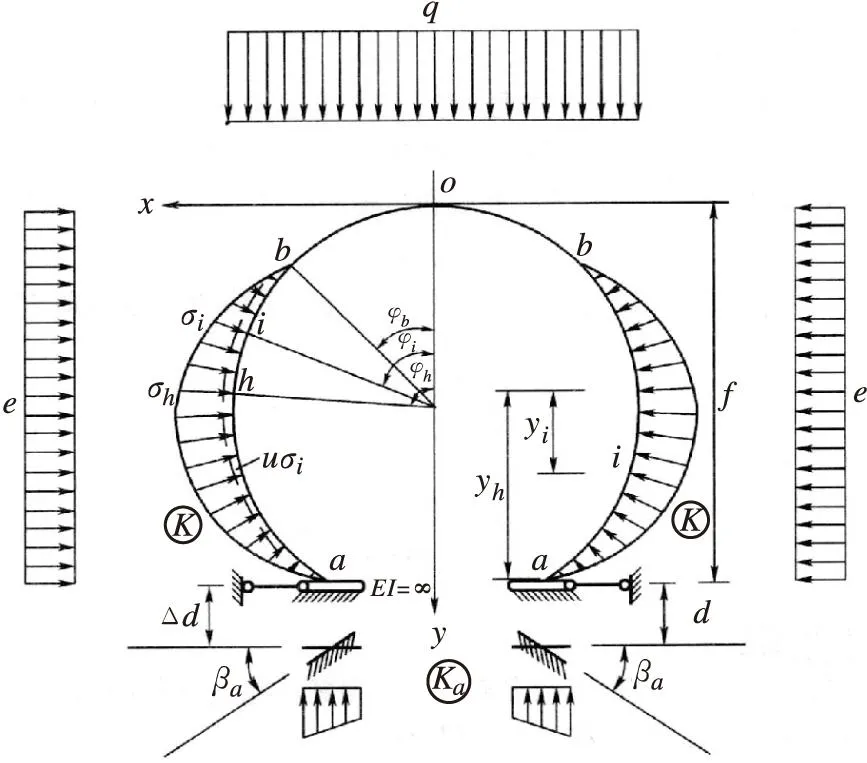
图1 曲墙式隧道模型示意图
2.2 计算模型
根据某大断面软岩特长公路隧道,曲墙段设计结构计算断面如图2所示,围岩的力学参数见表1。

表1 围岩及支护力学参数表
2.3 衬砌内力计算(计算图见下页图3)
2.3.1荷载确定[4]
(1)围岩竖向均布压力
我国《公路隧道设计规范》将围岩分为6级,其规定了围岩竖向均布压力:
q=0.45×2s-1γω
(1)
(2)围岩水平均布压力
参考《公路隧道设计规范》,本文中取围岩水平均布压力系数为0.4,计算公式为:
e=0.4q
(2)
(3)荷载确定
参考《公路隧道设计规范》,释放荷载分担比例见表2。

表2 释放荷载分担比例表[2]
由于本隧道围岩较差,故选取二次衬砌承担80%荷载来计算。
2.3.2位移计算
(1)单位位移
用辛普生法近似计算,单位位移计算公式如下:
(3)
(4)
(5)
(2)单位弹性抗力及相应的摩擦力引起的位移
(6)
(7)
(8)
(3)墙底(弹性地基上的刚性梁)位移
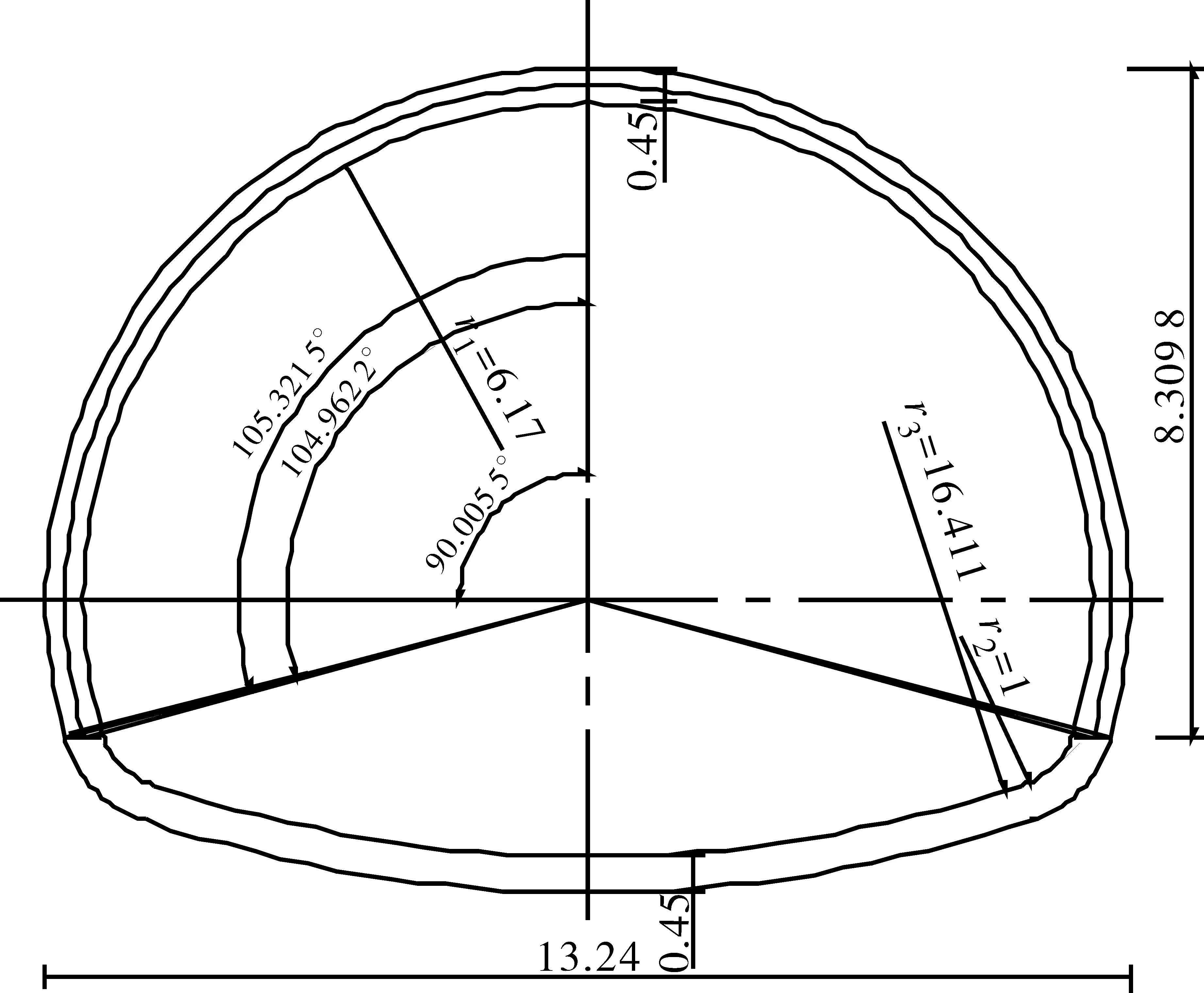
图2 曲墙式衬砌结构断面计算模型图

图3 衬砌结构计算图
单位弯矩作用下的转角:
(9)
主动荷载作用下的转角:
(10)
单位抗力及相应摩擦力作用下的转角:
(11)
2.3.3解力法方程
(12)
(13)
2.3.4主、被动荷载(σh=1)分别产生的衬砌内力
(14)
(15)
2.3.5衬砌总内力
(16)
2.4 计算结果
将计算结果弯矩M与轴力N按比例绘制成图,如图4所示:

图4 曲墙式衬砌结构内力图
3直墙式隧道衬砌结构计算
3.1 计算理论
拱形直墙式隧道衬砌的主要受力构件是拱圈和边墙,它们整体链接,而墙底支承在基岩上。另外,由于拱圈与边墙紧贴岩壁,因此围岩对其有弹性抗力作用。所以,在进行衬砌结构计算分析时,除考虑主动荷载外,还应考虑拱圈及边墙处弹性抗力的作用。
在计算时,需将拱圈和直墙分开考虑,即认为拱圈是一个拱脚弹性固定的无铰拱,拱圈弹性抗力假设为二次抛物线分布。边墙视为弹性地基梁,全部抗力由文克勒假设确定。墙顶和拱脚弹性固结,墙角与基岩间有较大的摩擦力,无水平位移发生,它在基岩上的作用,视为刚性体[2],如图5所示。
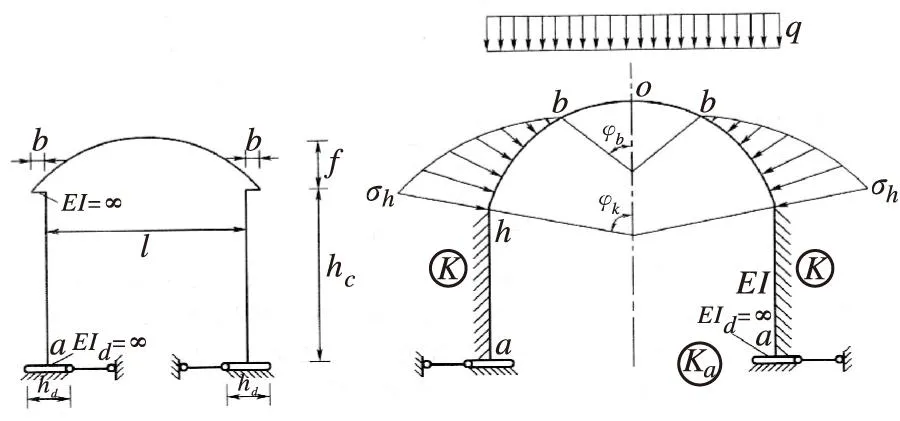
图5 直墙式隧道模型示意图
3.2 计算模型
直墙段设计结构计算断面如图6所示,围岩的力学参数与曲墙段一致,见前页表1。
3.3 衬砌内力计算(计算图见图7)
3.3.1主动荷载的确定
(1)围岩垂直均布压力
q1=0.45×2s-1γω
(19)
(2)超挖回填层重
q2=(平均超挖量)×γ
(20)

图6 直墙式衬砌结构断面计算模型图
(3)衬砌拱圈自重,近似取平均厚度,有:
(21)
综上所述,垂直荷载为:
q=q1+q2+q3
(22)
(4)围岩水平均布压力,本计算中取围岩水平均布压力系数为0.4,计算公式为:
e=0.4q
(23)
3.3.2位移计算
(1)单位位移
用辛普生法近似计算,单位位移计算公式如下:
(24)
(25)
(26)
(2)载位移Δ1p、Δ2p的计算
(27)
(28)
(3)弹性抗力位移Δ1σ、Δ2σ的计算
(29)
(30)
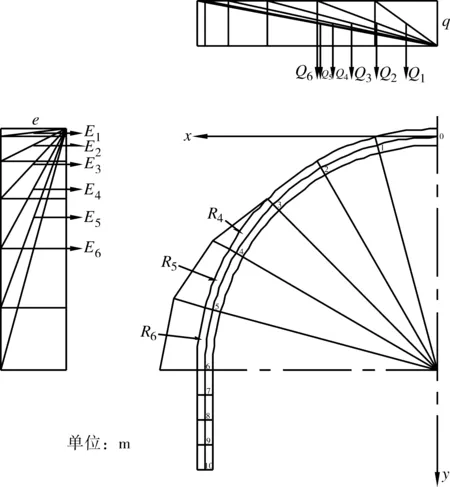
图7 衬砌结构计算图
(4)墙顶位移计算
将边墙看作是放置在弹性地基上的梁,对于弹性地基梁,按其相对长度al不同,可分为短梁、长梁和绝对刚性梁。因为本计算中1 墙顶位移采用下式进行计算: (31) (32) 3.3.3力法方程的求解 (33) (34) 3.3.4最大抗力值的求解 墙顶截面总水平位移用式(35)计算: uh=X1u1+X2(u2+fu1)+uZ (35) 最大抗力值为: σh=Kuh (36) 3.3.5拱部各截面的弯矩和轴力计算 弯矩的计算公式: (37) 轴力的计算公式: (38) 3.3.6边墙内力和弹性抗力的计算 (1)作用在墙顶截面的弯矩、水平力及垂直力 弯矩: (39) 水平力: (40) 垂直力: (41) (2)按弹性地基梁公式计算边墙的弯矩、轴力及抗力值 弯矩: (42) 轴力: Nx=Vh+xdwγh (43) 抗力: (44) 将计算结果弯矩M与轴力N按比例绘制成图,如图8所示: 图8 直墙式衬砌结构内力图 4计算结果对比分析 以上通过荷载结构法计算,得出的曲墙式隧道和直墙式隧道衬砌结构的弯矩图和轴力图。 通过图4和图8可以看出:曲边墙隧道的弯矩主要出现在拱顶、拱腰和边墙处,拱顶主要受压应力作用,而拱腰和边墙主要受拉应力的作用;最大弯矩在边墙处,为107.358 kN,拱顶的最大弯矩为96.457 kN,拱腰的最大弯矩为63.285 kN,相对较小。故需要加强对边墙和拱顶的支护。直边墙隧道的弯矩主要出现在拱顶、拱腰、边墙和墙脚处,拱顶和边墙主要受压应力作用,而拱腰和拱脚主要受拉应力的作用;最大弯矩在拱脚,为211.580 kN,产生了应力集中,拱顶的弯矩为181.079 kN,拱腰的最大弯矩为129.511 kN,边墙的最大弯矩为85.235 kN,相对较小;故需要加强对墙角和拱顶的支护。通过对比可以发现:采用曲边墙形式,衬砌的弯矩要远小于直边墙形式;曲边墙衬砌弯矩较均匀和对称,而直边墙弯矩变化较快,且墙脚处会出现应力集中现象;与曲边墙相比较,直边墙拱顶、边墙和墙脚处更加容易破坏。 在轴力上,曲边墙隧道的轴力从拱顶到墙角逐渐变大,最小轴力出现在拱顶处,约为1 125.645 kN,最大轴力出现在墙角处,约为1 289.443 kN;直边墙隧道的轴力从拱顶到墙脚亦逐渐变大,最小轴力出现在拱顶处,约为1 018.752 kN,最大轴力出现在墙脚处,约为1 477.606 kN;通过对比可以看出:曲边墙形式衬砌结构的轴力最大值与直边墙形式基本一致;曲边墙形式的轴力分布较为均匀,而直边墙形式的轴力变化稍大。 5结语 在隧道的施工过程中,采用直墙形式,施工简单,隧道主要承受竖向压力,但墙脚容易出现应力集中;采用曲墙形式,衬砌结构的弯矩小于直墙形式,且弯矩的变化幅度较均匀,其抗弯能力要优于直边墙形式。因此,考虑到结构受力的合理性以及施工和运营的安全性,设计和施工中要优先选用曲边墙形式。 参考文献 [1]夏鹏.大跨度黄土隧道洞口浅埋段支护效果研究[D].西安:长安大学,2010. [2]夏永旭,王永东.隧道结构力学计算[M].北京:人民交通出版社,2004. [3]姜安龙,胡斌,郭云英.盾构隧道衬砌结构设计方法研究[J].南昌航空工业学院学报(自然科学版),2007(3):73-78. [4]重庆交通科研设计院.公路隧道设计规范[S]. Research on Mechanical Properties of Soft Rock Tunnel Lining Structure with Different Section Types HU Xiao-ming,ZHOU Yong-di,JIA Yan-ling (Guangxi Transportation Research Institute,Nanning,Guangxi,530007) Abstract:For large-section in soft rock tunnel,to select the reasonable cross-section form and safe stable hole type is the safety basis to ensure the tunnel construction and future operation.By using the load structure method,this article calculated and analyzed the force of tunnel lining structure respectively using the straight sidewall and curved sidewall form,and obtained the conclusions that the force and bending of curved wall lining are better than straight wall lining. Keywords:Soft rock tunnel; Section types; Straight sidewall; Curved sidewall; Mechanical properties 收稿日期:2015-05-02 文章编号:1673-4874(2015)05-0045-05 中图分类号:U455.4 文献标识码:A DOI:10.13282/j.cnki.wccst.2015.05.013 作者简介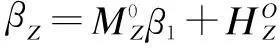
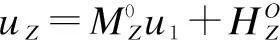
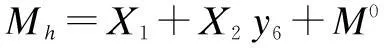
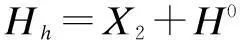
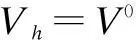

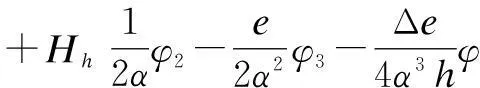

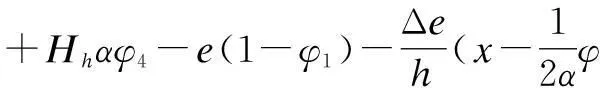
3.4 计算结果

