温度力作用下单元板式无砟轨道钢轨横向变形研究

刘　勇,杨荣山

(西南交通大学高速铁路线路工程教育部重点实验室,成都　610031)



温度力作用下单元板式无砟轨道钢轨横向变形研究

刘勇,杨荣山

(西南交通大学高速铁路线路工程教育部重点实验室,成都610031)

摘要：为了研究无砟轨道钢轨横向稳定性,以曲线上单元板式无砟轨道无缝线路为对象,建立包括钢轨、扣件、轨道板和限位部件的无砟轨道钢轨横向变形计算模型,结合不同轨道板长度分析钢轨在温度力作用下的横向变形特性,讨论不同、限位部件弹性和初始弯曲半波长对钢轨横向变形幅值和扣件横向抗力的影响。计算表明,巨大温度力可导致钢轨沿线路纵向产生以轨道板为波长的周期横向不平顺,在小半径曲线地段,应采用刚度较大且塑性变形小的弹性限位垫层材料,重视半波长过小的初始弯曲的治理,并加强对钢轨横向位移和板端扣件使用状态的监测。

关键词：温度力；单元板；无砟轨道；横向变形；稳定性

无缝线路是现代铁路轨道结构发展的重要技术之一，因其消灭了大量的钢轨接头，增加了线路的平顺性，大大减小了养护维修工作量，得到了广泛的应用[1]。但钢轨连续后，随着环境温度的变化，钢轨内部产生巨大的温度力，在曲线地段还存在较大的横向分力，导致钢轨产生横向变形[2]。若钢轨横向变形过大，不但影响行车安全性和舒适性，而且会缩减轨道各部件使用寿命，为后期运营维护带来更大经济负担。

对于有砟轨道的横向稳定性，相关的研究人员已做了大量的理论与试验研究[2，3]，迄今已形成较为成熟的“统一公式”和“不等波长公式”等无缝线路稳定理论检算方法。而对于无砟轨道，也有类似稳定性分析[4]，一般认为其基础稳固[5，6]，结构稳定性好，不会发生钢轨横向稳定性问题[7]，因此，对无砟轨道横向稳定性的研究较少。但近年来的现场观测发现[8]，在高温条件下，无砟轨道无缝线路也会产生一定的横向变形，主要以“碎弯”形式出现，虽然不会导致胀轨跑道，但会影响行车的平稳性。目前对于其无缝线路横向稳定性分析尚无成熟理论和统一检算标准。因此，分析无砟轨道钢轨横向变形特征，对预防和减小无砟轨道钢轨的横向变形，指导无砟轨道养护维修具有重要的理论和现实意义。

1横向变形模型

无砟轨道结构整体性强，基础稳固[9]，当钢轨的温度力过大且个别扣件工作状态不良时，在能量转移过程中，单元板式无砟轨道不会出现像有砟轨道胀轨跑道整体失稳的现象，而是在曲线地段钢轨以“碎弯”的形式达到平衡[10]。

1.1建立有限元模型

根据无砟轨道无缝线路扣件对钢轨纵横向的约束条件关系[10]，以曲线上单元板式无砟轨道无缝线路为例建立如图1所示的有限元分析模型。

模型视钢轨和轨道板为具有抗弯性能的2维梁单元，视扣件为具有纵、横向阻力的弹簧单元，视轨道板限位部件和CA(水泥乳化沥青)砂浆的纵、横向阻力均为弹簧单元，忽略砂浆垫层以下基础的横向变形，视为刚性。扣件间距取0.625 m，钢轨和轨道板以扣件节点间距的1/4划分单元。模型中的各阻力参数根据分析的需要均可设置为非线性阻力。

1.2边界处理及荷载施加

模型中圆曲线长度取200 m，缓和曲线因其曲率渐变，对结果影响较小，模型中简化处理。为了防止钢轨边界对计算结果的影响，在研究区段两端分别建立100 m直线段，并约束钢轨两端节点的纵横向位移和转角。

轨温变化作为外荷载，通过在钢轨单元上施加温度场实现。取钢轨升温50 ℃。

2计算参数

2.1扣件阻力

2.1.1扣件横向阻力

正常情况下，WJ-7型扣件受力传递机理为，钢轨横向分力通过绝缘轨距挡块传至铁垫板，然后通过板下摩擦传至道床；当横向力大于板下最大静摩擦力时，铁垫板开始滑动；当铁垫板与锚固螺栓接触时，横向力由绝缘轨距挡块经铁垫板和锚固螺栓传至道床。扣件横向阻力取决于绝缘轨距挡块的弹性支承力、铁垫板下摩阻力和锚固螺栓抗剪力。本计算假设扣件工作状态未达锚固螺栓抗剪阶段。

设绝缘轨距挡块弹性模量En=1.0×109Pa，与钢轨接触横向受力截面积An=100 mm×10 mm，厚Hn=10 mm，则绝缘轨距挡块提供的横向刚度Kn=EnAn/Hn=1.0×108N/m。

铁垫板下摩阻力可考虑为库伦摩擦力[10]。根据相关设计参数，锚固螺栓扭矩Mt取300 N·m；锚固螺栓扭矩系数k在一般加工表面有润滑时取0.15；锚固螺栓直径d取27 mm，单颗锚固螺栓的锚固力N0=Mt/kd=74.07 kN。忽略扣件自重等因素，钢轨每米质量mg为60.64 kg，则作用于一块铁垫板上的正压力为N=2N0+0.625mgg=148.52 kN。设铁垫板下摩擦系数μ=0.4，则板下摩阻力Fb=μN=59.4 kN。此时，绝缘轨距挡块最大变形量为Fb/Kn=0.6 mm。

垂向无载时，扣件横向极限阻力59.4 kN，弹塑性临界位移0.6 mm。

2.1.2扣件纵向阻力

参照《铁路无缝线路设计规范》[11]，当垂向无载时，WJ-7型扣件纵向阻力按双线性阻力形式考虑，取极限阻力15 kN，弹塑性临界位移2 mm。

2.2CA砂浆阻力

CA砂浆层是充填于板式无砟轨道中的关键结构层之一，起着调整、支承、传载、减振隔振等作用[12]。板下CA砂浆纵(横)向阻力用摩擦系数乘以单位长度轨道自重来表示，轨道自重为钢轨和轨道板自重之和。轨道板单元长度取为0.625÷4=0.156 25 m，根据西南交通大学现场试验数据，CA砂浆摩擦系数取0.56。沿线路中心线取半边模型，轨道单元长度上自重为98.502 kg，摩阻力为：Fc=μmg=0.56×98.502×9.8=540.58 N。与扣件纵向阻力规律类似，当轨道板与CA砂浆间的相对位移达到某一数值时，CA砂浆纵(横)向摩阻力将不继续增加，相对极限位移一般取为0.5 mm。

2.3限位部件阻力

参照《客运专线铁路CRTSⅠ型板式无砟轨道凸形挡台填充聚氨酯树脂暂行技术条件》[13]，100 mm×100 m m×25 mm试件的弹性系数约为10 kN/ mm，弹性模量约为25 MPa。凸形挡台半径260 mm，高度190 mm，填充层厚40 mm，高度取低于轨道板面10 mm，则半边模型中弹性限位垫层提供的纵横向刚度为29.25 kN/mm。

3计算结果及分析

3.1温度力作用下钢轨横向变形特性分析

当曲线半径R=500 m时，分别选取单元板长度为5、7.5 m和10 m的板式轨道结构形式，在温度力作用下，不同单元板长度的钢轨横向变形(r向，下同)如图2所示，不同单元板长度的扣件横向抗力如图3所示。

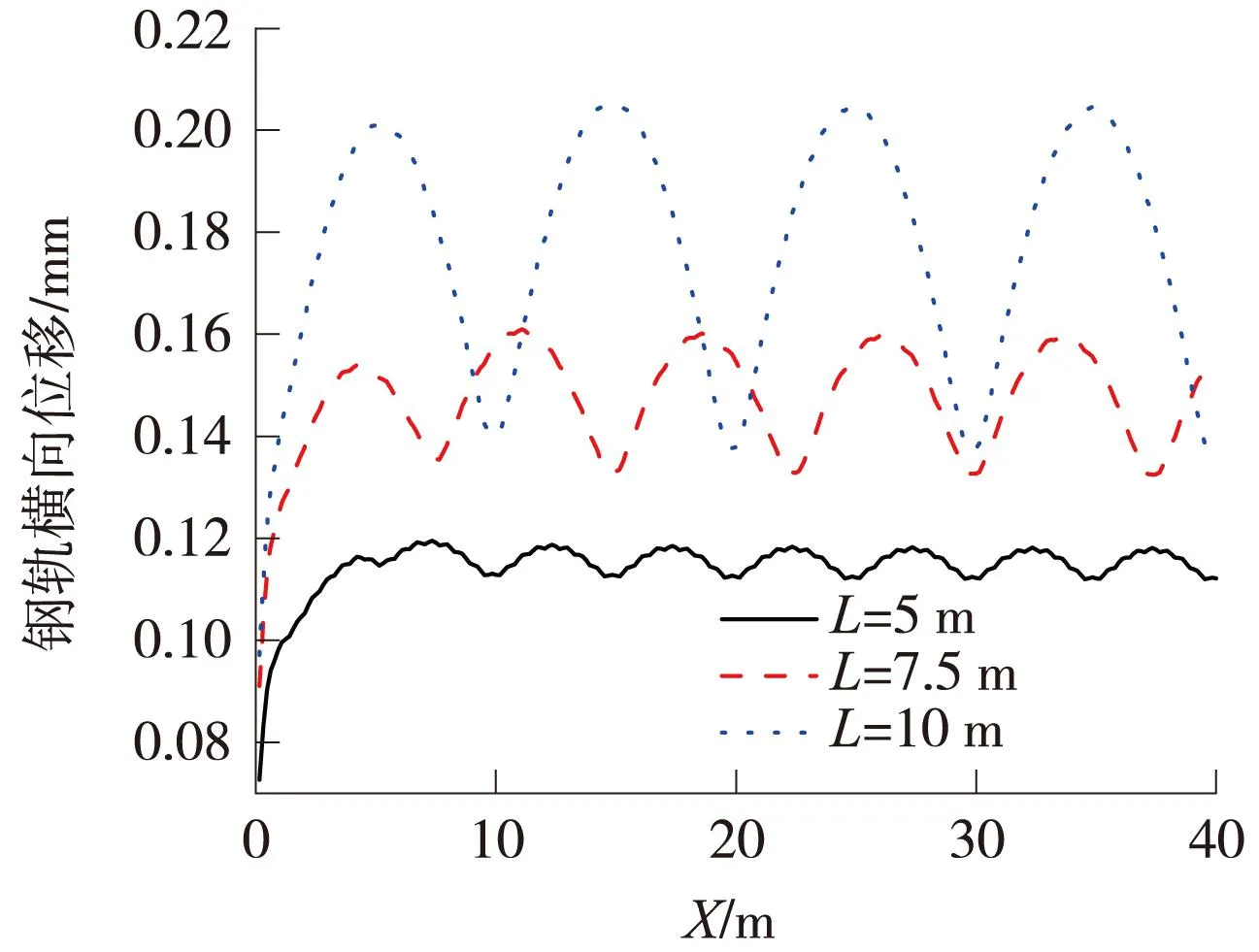
图2　不同单元板长度的钢轨横向位移(局部)

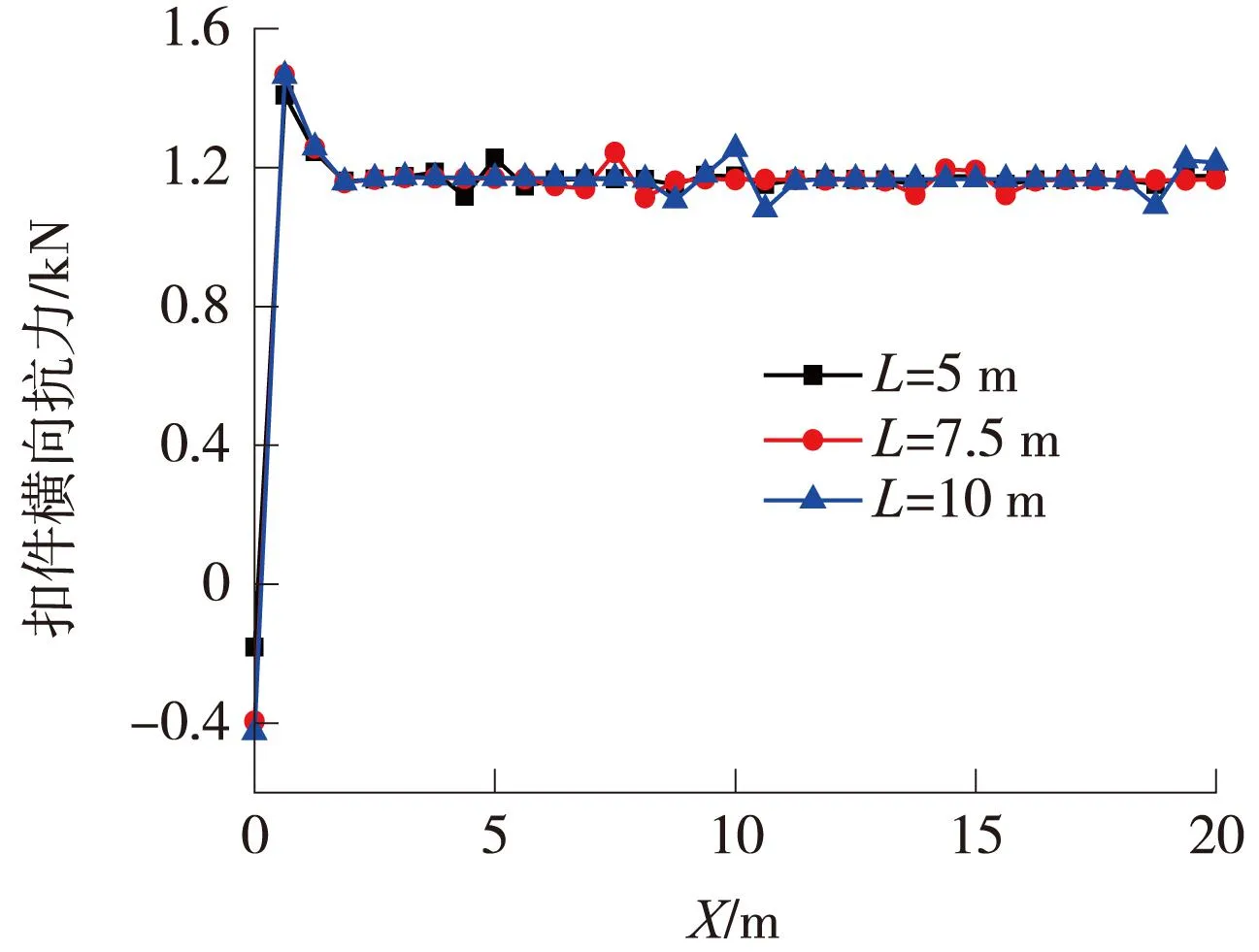
图3　不同单元板长度的扣件横向抗力(局部)

由图2可知，钢轨在温度力作用下发生了横向变形，从曲线端部开始迅速增大，在第二块轨道板中部处达到最大。随着单元板长度的增大，钢轨的最大横向位移也随之增大。钢轨横向位移整体上呈周期变化，使得钢轨沿线路方向具有波长为一个轨道板长度的方向不平顺。由图3可知，扣件横向抗力也从曲线端部开始迅速增大，轨道板中部趋于稳定。随着单元板长度的增大，扣件横向力以单元板长度为波长呈周期性变化规律越发明显，板端处的扣件横向力大于板中部，差值也越来越大。说明在温度力作用下，板端处扣件更容易受损。

3.2限位垫层弹性模量的影响

轨道结构其他参数保持不变，改变限位垫层弹性模量即修改限位部件阻力弹簧线刚度，当弹性模量为25、50、75 MPa和100 MPa时，不同限位垫层弹性模量对钢轨横向变形影响如图4所示，对扣件横向抗力影响如图5所示。

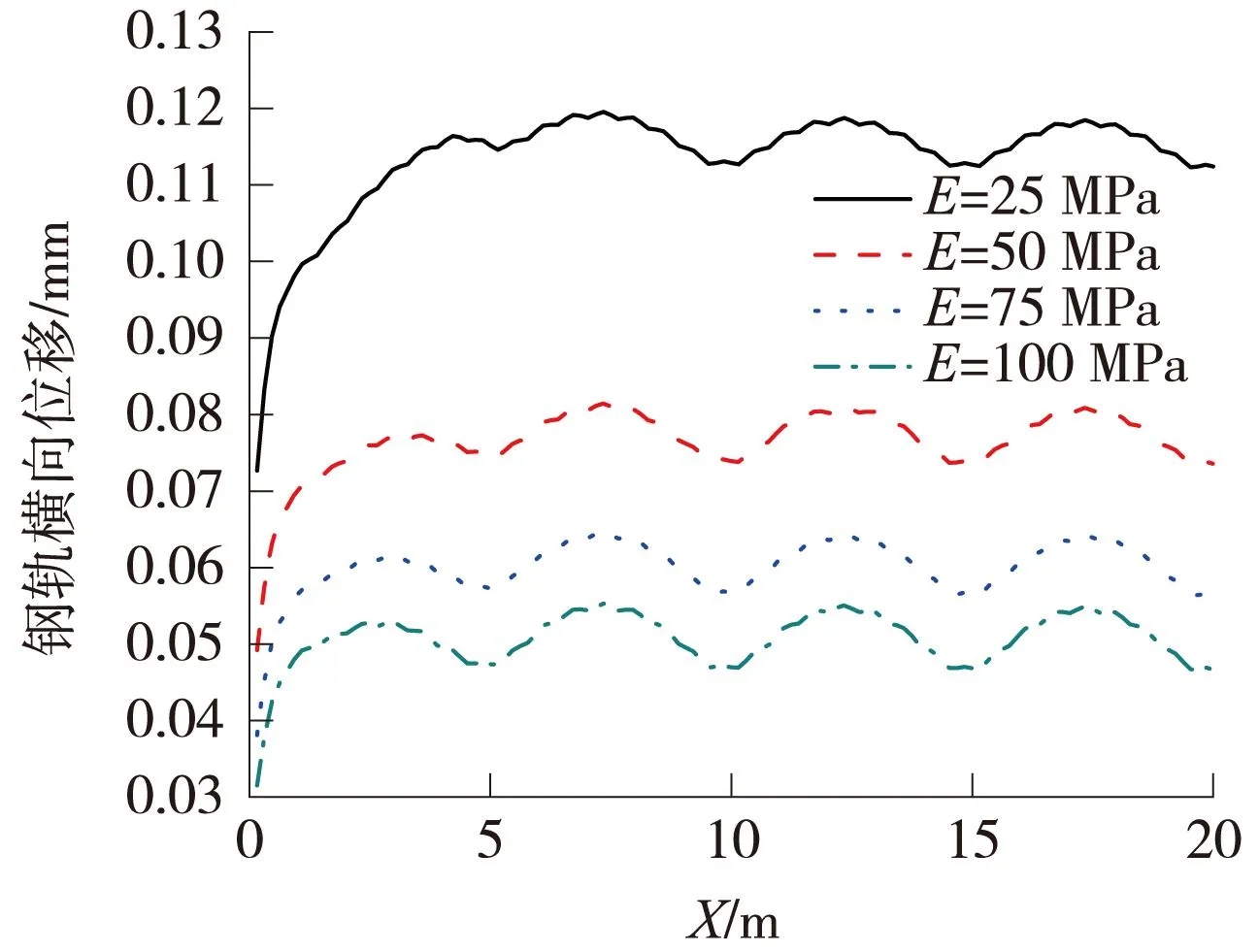
图4　不同限位垫层弹性模量的钢轨横向位移(局部)

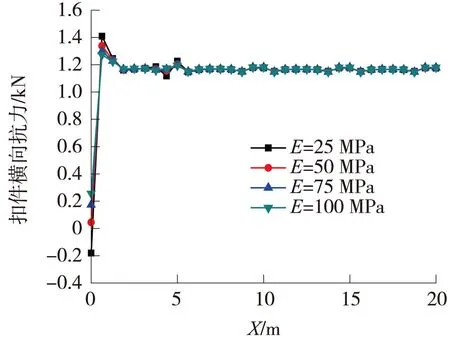
图5　不同限位垫层弹性模量的扣件横向抗力(局部)

由图4可知，当限位垫层弹性模量E=25 MPa时，钢轨最大横向位移为0.120 mm。随着限位垫层弹性模量的增大，钢轨的最大横向位移随之减小，减小幅度也越来越小，当限位垫层弹性模量E=100 MPa时，钢轨最大横向位移为0.055 mm。由图5可知，限位垫层弹性模量的改变对扣件横向抗力几乎没影响。说明曲线地段可通过适当增大限位垫层弹性模量来增强轨道结构的整体稳定性，以达到减小钢轨横向位移的作用。

3.3初始不平顺波长的影响

根据统一公式，假设轨道弹性初始弯曲为半波正弦曲线[14]，并发生在圆曲线中部。以常见的弹性初始弯曲矢度3 mm为例，轨道结构其他参数保持不变，当弹性初始弯曲半波长为2、3、4、5、6、7 m和8 m时，不同初始弯曲半波长对钢轨最大横向变形影响如图6所示，对扣件最大横向抗力影响如图7所示。

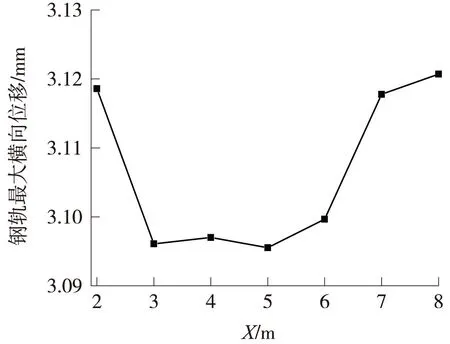
图6　不同初始弯曲半波长的钢轨最大横向位移(f=3 mm)

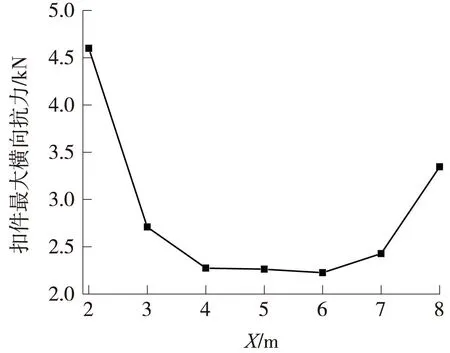
图7　不同初始弯曲半波长的扣件最大横向抗力(f=3 mm)

由图6和图7可知，当初始弯曲半波长l=2 m时，钢轨最大横向位移为3.119 mm，扣件最大横向抗力为4.6 kN。随着初始弯曲半波长的增大，钢轨最大横向位移和扣件最大横向抗力均先减小后增大。当初始半波长l=5 m(单元板长)时，钢轨最大横向位移达最小3.096 mm，之后又随初始弯曲半波长增大而增大；初始弯曲半波长为6 m时，扣件最大横向抗力达最小2.2 kN，之后也随初始弯曲半波长增大而增大。说明初始弯曲半波长与单元板长度接近时，对钢轨横向位移和扣件横向抗力影响最小，现场应注意半波长过小的初始弯曲的治理。

4结论

(1)对于结构各部件完好的无砟轨道无缝线路，即使在小半径曲线地段，钢轨的初始不平顺和限位垫层的弹性模量对无缝线路稳定性的影响都很小。

(2)在温度荷载作用下，由于温度力横向分力的作用，位于一定半径曲线上单元板式轨道结构的钢轨会发生横向变形，整体上呈周期性变化，最大横向位移发生在第二块轨道板中部位置，沿线路方向具有波长为一个轨道板长度的方向不平顺。从钢轨横向位移和扣件横向疲劳受损考虑，单元板长度不宜过长。

(3)限位部件弹性与钢轨横向位移呈反相关，对扣件横向抗力几乎无影响。在曲线地段，应采用刚度较大且塑性变形小的弹性限位垫层材料，通过增大轨道结构的整体稳定性，来有效预防幅值较大的碎弯变形。

(4)圆曲线半径与钢轨横向位移和扣件横向抗力均呈反相关，二者均在初始弯曲半波长与单元板长相近时达最小值。因此，在小半径曲线上，现场应重视半波长过小的初始弯曲的治理，并加强对钢轨横向位移和板端扣件横向抗力的监测。

参考文献：

[1]广钟岩，高慧安.铁路无缝线路[M].北京:中国铁道出版社，2005:1-4．

[2]卢耀荣.无缝线路研究与应用[M].北京:中国铁道出版社，2004:70-97.

[3]张向民，陈秀方，杨小礼.荷载变形关系求解无缝线路轨道稳定性[J].工程力学，2007，24(6):189-192,116.

[4]赵立宁，蔡小培，曲村.地面沉降对路基上单元板式无砟轨道平顺性的影响分析[J].铁道标准设计，2013(10):15-18.

[5]Coenraad Esveld. Modern railway track(second edition) [M]. Delft： Koninklijke van de Garde BV， 2001:231-233.

[6]何华武.无砟轨道技术[M].北京:中国铁道出版社，2005:15-16.

[7]刘丹，李培刚，赵坪锐.无砟轨道结构整体失稳可能性探讨[J].铁道建筑，2011(10):95-98.

[8]高亮.高速铁路无缝线路关键技术研究与应用[M].北京：中国铁道出版社，2012:33-35．

[9]Zhang Shuguang. Study on technology system and system integration method of China high-speed railway[C]∥Proceedings of the ASME Joint Rail Conference 2010， JRC， 2010:501-506.

[10]肖杰灵，郭利康，刘学毅.无砟轨道钢轨碎弯成因分析[J].铁道建筑，2009(2):93-96.

[11]中华人民共和国铁道部.TB10015—2012铁路无缝线路设计规范[S].北京:中国铁道出版社，2013．

[12]徐浩，王平，曾晓辉.高速铁路板式无砟轨道CA砂浆研究现状与展望[J].铁道标准设计，2013(11)：1-5,10.

[13]中华人民共和国铁道部.科技基2008—74号客运专线铁路CRTSⅠ型板式无砟轨道凸形挡台填充聚氨酯树脂(CPU)暂行技术条件[S].北京:中国铁道出版社，2008．

[14]杨荣山.轨道工程[M].北京:人民交通出版社，2013：166-170.

Study on Lateral Deformation of Rails in Unit Slab Ballastless Track under Temperature ForceLIU Yong, YANG Rong-shan

(MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Abstract：In order to study the rail lateral stability of the ballastless track, CWR unit slab ballastless track on the curve is analyzed to establish a calculation mode for lateral deformation of the rail in ballastless track including rail, fastener, track slab and spacing parts. With reference to different lengths of track slab and the lateral deformation characteristics of the rail under temperature force, this paper addresses the effect of different elasticity of limiting parts and initial bending half-wavelength on lateral deformation amplitude value of the rail and on lateral resistance of fasteners. The calculation shows that periodic transverse irregularities of the rail are caused by significant temperature force in longitudinal direction of the line and along the length of track slab. Therefore, the underlay spacing materials with larger rigidity and smaller plastic deformation shall be used on curved sections of small radius. Treatment of initial bending with undersized half wavelength shall be emphasized and monitoring of transverse displacement of the rail and the fasteners at the ends of slab shall be reinforced.

Key words：Temperature force; Unit slab; Ballastless track; Lateral deformation; Stability

中图分类号：U213.2+44； U213.4

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2015.01.008

文章编号：1004-2954(2015)01-0033-04

作者简介：刘勇(1990—)，男，硕士研究生。

基金项目：国家自然科学基金(51278431)；中国铁路总公司科技开发计

收稿日期：2014-05-09； 修回日期：2014-05-25

划项目(2013G008-C)