土堤式挡风墙加高挡板稳定性分析及研究

朱文智,程建军,张云鹏,景文宏,蒋富强

(1.石河子大学水利建筑工程学院,新疆石河子832003； 2.中铁西北科学研究院有限公司,兰州　730000)



土堤式挡风墙加高挡板稳定性分析及研究

朱文智1,程建军1,张云鹏1,景文宏1,蒋富强2

(1.石河子大学水利建筑工程学院,新疆石河子832003； 2.中铁西北科学研究院有限公司,兰州730000)

摘要：在强风以及沙粒共同冲击作用的条件下,为了确定既有土堤式挡风墙加高挡板在各风速下的固定形式,寻找其在风沙两相流情况下的一种安全埋深计算方法。应用数值模拟软件对不同风速下加高挡板周围流场进行分析,探讨流场规律。分别计算风荷载与沙荷载作用下加高挡板的受力,并计算其支座反力,最终确定其在极限条件下埋置深度的近似计算方法,为铁路安全运行与防风沙设计提供参考与依据。

关键词：挡风墙；沙荷载；风荷载；数值模拟；埋深计算

戈壁是荒漠的一种类型，戈壁地区气候干燥，地势平缓，植被覆盖度极低，表面多为砾石所覆盖。地表常年受到自然力量的侵蚀。被侵蚀后的岩石形成细小的沙物质。由于地表粗糙度小，该区域通常大风频繁并且风速大。处于山谷前后的戈壁地区由于“狭管效应”或顺风向下沉的地势，风力更是强劲。大风携带着沙形成风沙流。强风沙流对于地表植物、构筑物、线路上运行的车辆破坏力大。风沙流为沙漠提供了物质补给同时也为沙漠的移动提供了驱动力[1]。新疆铁路多修建于沙漠戈壁，常年受西伯利亚冷空气南下的影响，风沙流破坏力强。铁路所经处附近有大量沙源[2]。对新疆铁路影响较强的风区主要有：兰新线西段百里风区(雅子泉至红旗坎站间)，南疆线前百公里风区，吐鲁番至鱼儿沟站间。根据历史资料，南疆线前百公里最大瞬时风速达64 m/s，百里风区最大瞬时风速达60 m/s。唐士晟[3]对该地段大风特征进行统计分析，发现该地区具有风速大、风期长、季节性强、风起动速度快等规律。

我国兰新线风区铁路长达525 km，为全线总长的54%。据相关资料统计，自1960年至1993年大风吹翻列车13起，共计翻车79辆[4]。风沙流对铁路运输的安全，国家财产有很大的威胁。为此在上述线路段修筑了挡风阻沙设施挡风墙。

为了保证风沙条件下机车的安全运行，许多国家都进行了研究，取得了较大进展。在工程应用当中，主要是从两方面进行防护。一是布设线路周围的防护设施，二是制定机车的运行管理规则。虽然2种方法相结合取得了很大成效，但为了适应快节奏、高效率的运输要求，安全、合理的防护措施就显得更为重要。现今兰新铁路上挡风墙种类有：土堤式挡风墙、对拉式挡风墙、柱板式挡风墙、“L”式挡风墙。挡风墙的种类和类型决定挡风的效果。

庞巧东[5]对不同种类的挡风墙的挡风效果进行了数值模拟与野外试验，并进行了详细的对比，结果表明土堤式挡风墙背风侧不能形成明显的涡流区，同风速下挡风墙厚度与涡流区长度成正比。对拉式挡风墙优于“L”式挡风墙优于土堤式挡风墙。程建军[6]对该地区戈壁铁路沿线的风沙地貌、线路沙害表现形式、既有防风沙工程功效进行实地调查与现场测试，分析挡风墙后的风速剖面变化与流场变化特征。结果表明:对于相同高度挡风墙，其大风遮蔽效应系数会随着墙后距离的增加逐渐减弱，高点位高程水平向的速度衰减快于低点位高程水平向的风速衰减。

多项研究显示土堤式挡风墙的效果不理想，为此有必要对既有的土堤式挡风墙进行结构改造，使其满足大风情况下列车的运行安全。现阶段，新疆大风区域内的铁路沿线土堤式挡风墙采用的改造形式是在既有挡墙的顶部中间位置加设高1 m，宽0.15 m的挡板。为了分析加高挡板对流场的影响程度，以及加高挡板的力学性质和固定形式，结合现场实测风况数据首次对土堤式挡风墙加高挡板进行了计算分析。

1土堤式挡风墙优化的目的与方法

1.1研究目的

通过目前对既有土堤式挡风墙改造的研究基础上，运用CFD软件分析加高挡板背风侧流场特性。包括对风速场，压强场的分析。使用大风遮蔽效应系数[6]作为衡量挡风效果的参量，从而对比各类型挡风墙的挡风性能。分析加高挡板的受力类型和大小，建立计算加高挡板安全埋深的理论方法。保证改造后的土堤式挡风墙的使用安全。

1.2研究方法

主要采用数值模拟的方法对改造后的土堤式挡风墙进行数值分析，通过建立模型、模型离散化、建立离散化方程、迭代求解、数据处理等过程对挡风墙流场、压强场进行分析。通过数值模拟得到流场中的风速、压强数据，结合工程实测的风沙流密度数据，应用结构力学、土力学、流体力学原理计算加高挡板的受力、支座反力，最终确定其固定埋置深度。

2研究内容

2.1改造形式

兰新铁路既有土堤式挡风墙高度为3.0 m，顶部宽为1 m，左右边坡坡率都为1∶1.5。在其两侧边坡都覆盖有C15混凝土预制板，其尺寸为500 mm×500 mm×8 mm，用来防止大风对挡风墙的风蚀作用。土堤式挡风墙详见图1。挡风墙最终的改造形式是在其顶部的中部位置加设高度为1 m的柱板式挡墙。柱的尺寸为300 mm×300 mm，板的厚度为150 mm，柱与柱之间的距离为1.5 m，材料均为钢筋混凝土。加高挡板的柱埋置在土堤式挡风墙顶部中间位置。改造后的土堤式挡风墙如图2所示。

图1　既有土堤式挡风墙

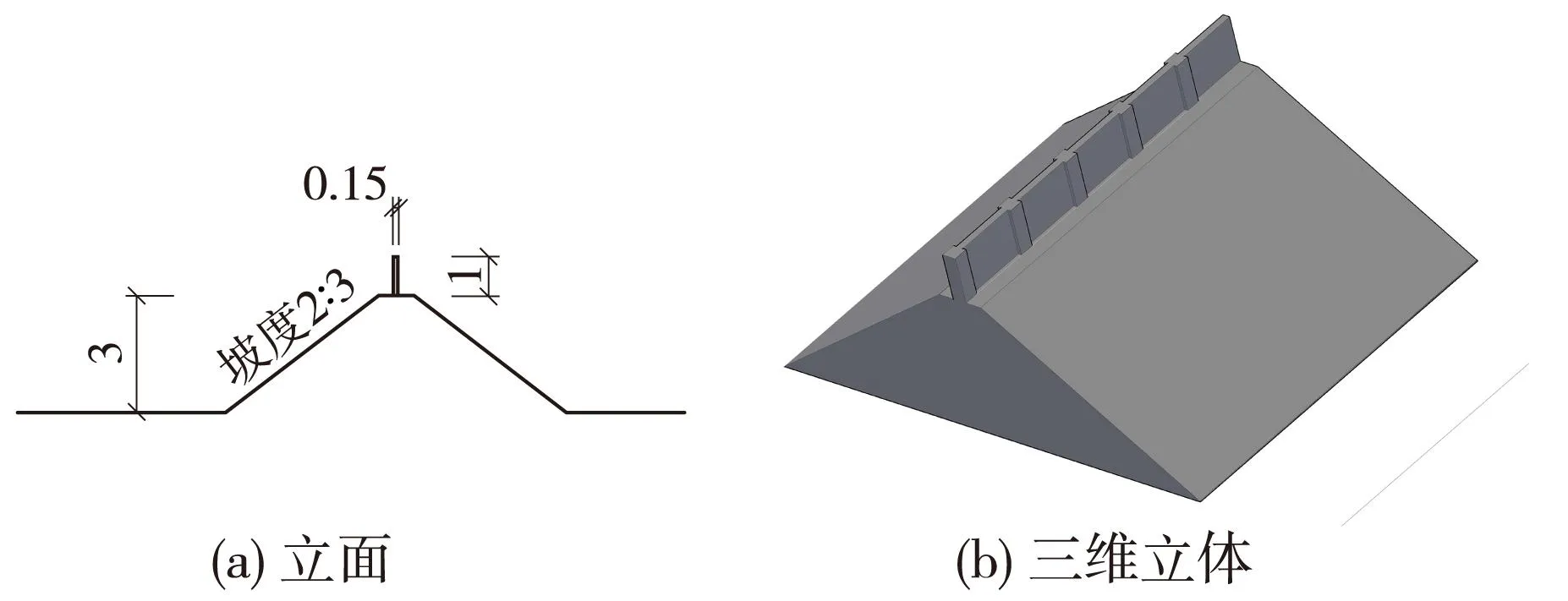
图2　改造后土堤式挡风墙模型(单位：m)

2.2加高挡板固定形式及稳定性计算

为了确定加高挡板立柱的具体埋深，需要分析加高挡板所受荷载的种类及大小。应用流体力学、结构力学、土力学的相关知识，并结合野外实测数据对加高挡板埋深建立理论近似计算公式。

2.2.1荷载的种类

建(构)筑物在设计建造时必须要考虑其本身的抗风沙荷载稳定性，但《建筑结构荷载规范》(GB50009—2012)[7]中仅仅要求计算净风荷载而忽略大风所携沙粒对建筑的冲击荷载，这在风沙流密度与风速较低的情况下是可以接受的，但因为戈壁地区地质物理环境的特殊，风速、风沙流密度大，风沙流结构分布也有异于其他区域。沙物质不仅仅集中在地表附近，大风携沙高度可达8 m以上。当风速达到一定值后，沙荷载甚至大于风荷载。所以沙荷载在计算中应该考虑。故挡风墙加高挡板受到的主要荷载有：风荷载、沙荷载。

2.2.2风荷载的计算

建筑物表面实际受到的风压称为风荷载，风荷载是一种随机作用，包括了基本风压和脉动风引起的等效风压。本文中采用数值模拟的方法确定极限条件下的风荷载。数值模拟中风速的最大值为50 m/s，最低风速取15 m/s，以5 m/s为一个增量，一共计算9种风速条件下的挡板受力。首先确定加高挡板单位长度所受到的风荷载和沙荷载，从而得到立柱受到板传递来的荷载。

图3　风荷载计算简图

以最大风速50 m/s为例。相邻节点之间风荷载可以划分为矩形部分和三角形部分，两部分的叠加则为两节点间的风荷载。由图3可以直观地看出加高挡板迎风面与背风面的风荷载。矩形部分单位长度荷载计算公式为

三角形部分单位长度荷载计算公式为

式中，Fij，1为i，j两节点间矩形部分单位长度的荷载，N；Mij，1为i，j两节点间矩形部分单位长度的荷载对埋置位置的弯矩，N·m；h1为矩形中合力作用点到埋置位置的高度，m；Fij，2为i，j两节点间三角形部分单位长度的荷载大小，N；Mij2为i，j两节点间三角形部分单位长度的荷载对埋置位置的弯矩，N·m；h2为三角形中合力作用点到埋置位置的高度，m；pmin为i，j两节点上压强较小的节点压强，Pa；pmax为i，j两节点上压强较大的节点压强，Pa；Δh为i，j两节点的竖直高度，m。

叠加后的单位长度加高挡板风荷载大小为∑F=3 334.67 N/m，其值同时也是埋置位置单位长度板断面的剪力大小。叠加后的风荷载对加高挡板埋置位置的弯矩大小为∑M=1 472.13((N·m)/m)。

所有风速下的加高挡板风荷载大小与叠加后的风荷载对加高挡板埋置位置的弯矩大小统计见表1。

2.2.3沙荷载的计算

建筑物表面受到高速沙粒的冲击压称为沙荷载，

表1　风荷载及支座弯矩计算

本文应用动量定理推导沙荷载的大小。假设高速运动的沙粒为形状规则，大小均一的圆形颗粒，沙粒与结构的冲击看作完全弹性碰撞，碰撞方向为垂直挡板表面，反弹速度与冲撞速度一致。根据动量定理有

公式变换为

2mvi=F·Δt

m为Δt时间内撞击挡风墙的颗粒质量，由风沙流密度与沙粒速度的关系式可以知道

式中，m为沙粒的质量，kg；vi为沙粒运动的速度，m/s；Δt为撞击时间，s；F为碰撞作用力，N；s为接触面积，m2；ρ为风沙流密度，g/m3。

经过公式变换，沙粒撞击挡风墙的冲击压强为

Fs=ps·h

式中，ps为沙荷载的冲击压强，Pa；h为加高挡板的高度(h=1 m)；Fs为单位长度加高挡板的水平荷载，N。

风沙流密度与风速、高度、地质环境、地貌环境都有较大的关系。风沙流密度随高度的增加呈现下降趋势，在分界点之下，下降趋势较剧烈。分界点以上，下降趋势较平缓。随着风速的继续增大，风沙流密度的分界点也会向上移动。所以沙粒的冲击压强计算公式中的风沙流密度并非定值。为了简化计算，冲击荷载中的风沙流密度将沙害较为严重的“十三间房”作为参照。应用该地区风沙流密度拟合方程

可以得到风速为50 m/s时3 m高处风沙流密度为ρ=18.03 g/m3。最终得到单位长度加高挡板沙荷载大小为Fs=90.2(N/m)。叠加后的沙荷载对单位长度加高挡板埋置位置的弯矩大小为Ms=45.1(N·m)/m)。

所有风速下的加高挡板沙荷载大小与沙荷载对加高挡板埋置位置的弯矩大小统计见表2。

表2　沙荷载及支座弯矩计算

2.2.4柱埋深计算

加高挡板采用钢筋混凝土制作而成，研究其受力时可视其为刚体。填埋材料为人工填土，研究其受力时可以看作弹性体。加高挡板将受到的风荷载、沙荷载传递给立柱，立柱再将荷载传递给土体。土地受到柱的侧向挤压，从而反作用于立柱，保证立柱的稳定。由于立柱的重力，摩擦阻力数值较小，予以忽略。计算方法是：在假定埋深的条件下通过计算立柱对土体的最大压应力，使之小于被动土压力与主动土压力之差，即可满足加高挡板的固定要求。

在加高挡板上，单根立柱受到的风荷载为：1.8×∑F=6 081.10 N；沙荷载为：1.8×Fs=162.27 N。折算为柱在埋置位置断面处的剪力Q0=8 180.5+162.3=8 342.8(N)；柱在埋置位置断面处的弯矩M0=(1.8×1 998.6)+(1.8×45.1)=3 678.7(N·m)。

图4为立柱埋深的计算示意图，柱的变位为ΔX，计算公式为

因为变形较小，所以tanφ可以用φ替代。土体所受到的侧应力σy可以表示为

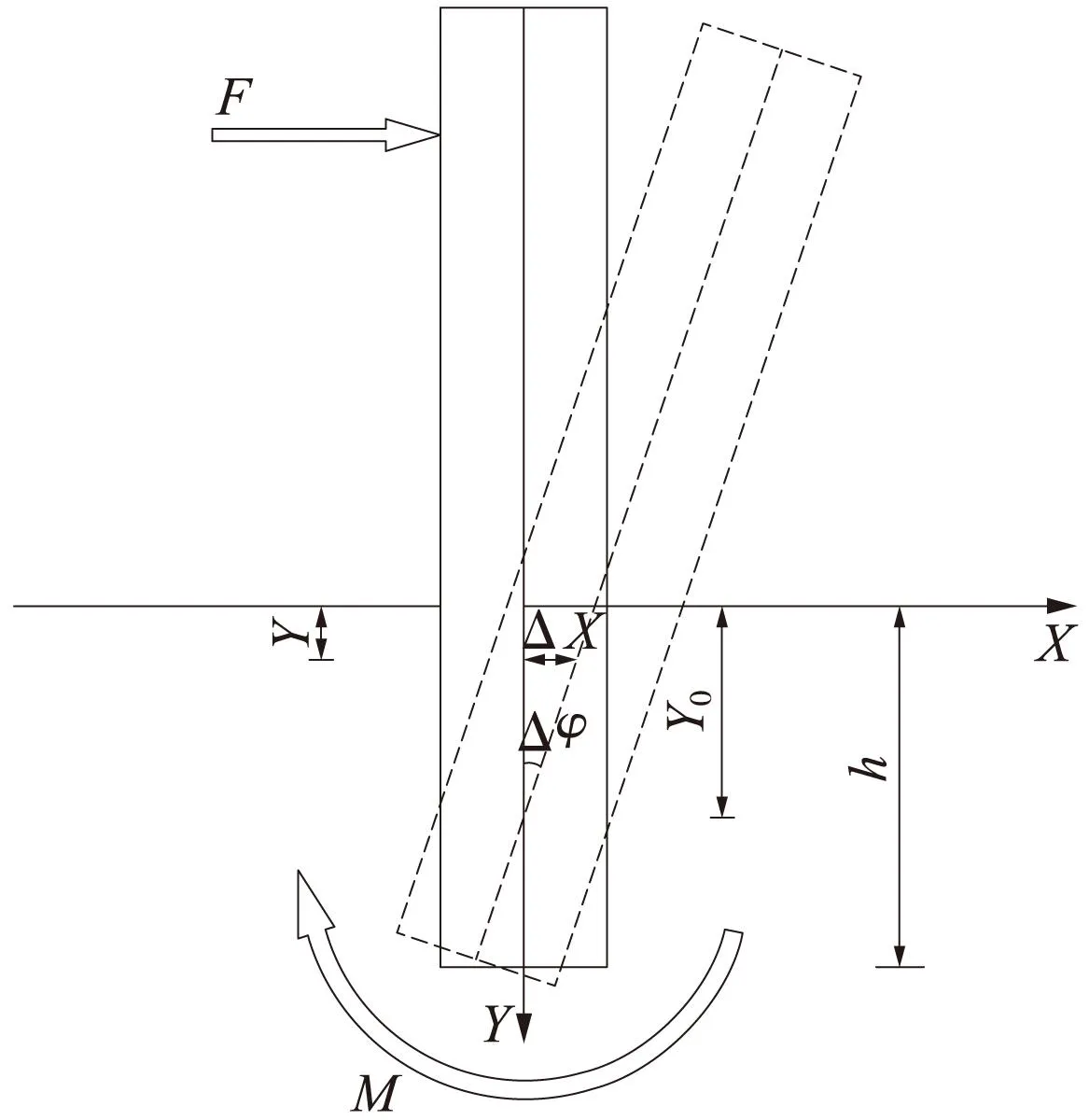
图4　立柱埋深计算示意

柱的剪力Qy的计算公式如下

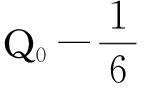
弯矩计算公式

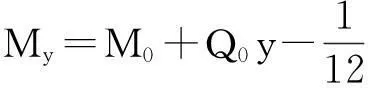
在柱受到荷载时，根据柱底的边界条件，剪力、弯矩分别为零，得出

对侧应力公式中y进行求导，令导函数为零。求出在什么位置达到侧应力极限值。

上述各式中，h为柱子的埋深；m为土的侧向地基系数随深度的变化比例系数，kN·m-4，人工填土m视为10 000(kN·m-4)；y0为旋转中心至埋置位置的距离；Δφ为旋转角度；Bp为柱子的计算宽度，矩形柱，Bp=b+1(b为正截面长)。

被动土压力计算公式

主动土压力计算公式

被动土压力与主动土压力之差

式中，γ为地基土容重，kN·m-3;φ为地基土的内摩擦角，(°)；C为地基土的单位黏聚力，kN·m-2，人工填土可以取0。

柱的埋深设定为1 m，将荷载值代入上述算式中进行计算

y0=0.72mΔφ=0.013 8°σmax=16.85kPa

沙的容重按18kN·m-3，内摩擦角按30°，黏聚力为0。

上述算例说明：加高挡板埋深在1m时，可以满足风速在50m/s以下各工况加高挡板的埋深安全要求。在各风速条件下，立柱对土体的最大压应力，以及被动土压力与主动土压力差值如表3所示。

表3　侧应力极限值及被动土压力与主动土压力之差计算　kPa

由此可知，当风速在55 m/s时，挡板埋深1 m已经不能满足最小埋深的要求。将埋深h=1.2 m代入上式，可以得到在风速为55 m/s时的σmax=17.26 kPa，σp-σa=18.44 kPa。σmax<σp-σa，则说明1.2 m的埋深满足要求。

3结论

通过对改造后土堤式挡风墙的数值模拟，以及相关的公式推导，得到了关于土堤式挡风墙加高挡板所受到的风荷载、沙荷载的规律。推导出加高挡板的安全埋深近似计算方法。主要结论如下。

(1)沙荷载的大小与风沙流密度、风速大小关系密切相关。在风沙流密度不变时，风速低于某一数值时，沙荷载的大小可以忽略不计，当风速大于该风速值时，沙荷载随着风速的增大迅速增大，以至于超过沙荷载的作用效果。

(2)在考虑风荷载与沙荷载的共同作用下，改造后的土堤式挡风墙加高挡板的安全埋深可以参照本文的算式进行近似计算。在典型区域内风沙两相流的作用下，通过计算得出：在风速不大于50 m/s的情况下，按照实际工程中的加高挡板的材料和尺寸，加高挡板的立柱埋深在1.2 m可以满足设计安全要求。对既有土堤式挡风墙加高挡板的埋深提出的理论近似计算方法，可以为将来类似防风沙工程优化设计提供参考和依据。

参考文献：

[1]葛盛昌，蒋富强.兰新铁路强风地区风沙成因及挡风墙防风效果分析[J].铁道工程学报，2009(5):1-4.

[2]孙庆伟，王涛，韩致文，等.北疆铁路沿线风沙危害的研究[J].中国沙漠，2004，24(3):182-186．

[3]唐士晟，史永革，张小勇.新疆铁路百里风区大风特征统计分析[J].铁道技术监督，2011，39(1):36-40．

[4]尹永顺，王厚雄.兰新复线防风安全工程研究报告[R].乌鲁木齐:乌鲁木齐铁路局，1993．

[5]庞巧东，程建军，蒋富强，等.戈壁铁路挡风墙背风侧流场特征与挡风功效研究[J].铁道标准设计，2011(2):1-5．

[6]程建军，蒋富强，杨印海，等.戈壁铁路沿线风沙灾害特征与挡风沙措施及功效研究[J].中国铁道科学，2010，32(5):15-20．

[7]中华人民共和国住房和城乡建设部.GB50009—2012建筑结构荷载规范[S].北京:中国建筑工业出版社，2012．

[8]蒋富强，邸耀全，张红利.沙障立柱受力分析及埋深计算[J].中国沙漠，1999，19(2):187-190.

[9]钱征宇.西北地区铁路大风灾害及其防治对策[J].中国铁路，2009，(3):1-4．

[10]杨斌，刘堂红，杨明智.大风区铁路挡风墙合理设置[J].铁道科学与工程学报，2011(3):67-72.

[11]Araujo A D， Andrade J S， Maia L P， et al. Efficiency of sediment samplers for wind erosion measurement[J]. Granular Matterr， 2009(9):131-139.

[12]Bagnold R A. The physics of blown sand and desert dunes[M]. London: Methuen， 1941:255-259.

[13]黄本才，汪从军.结构抗风分析原理及应用[M].上海:同济大学出版社，2008:26-33.

Analysis and Research on the Stability of Earth Embankment Wind-break Wall with High Dam BoardZHU Wen-zhi1, CHENG Jian-jun1, ZHANG Yun-peng1, JING Wen-hong1, JIANG Fu-qiang2

(1.College of Water Resources and Architectural Engineering, Shihezi University, Shihezi 832003, China;

2.Northwest Research Institute Co., Ltd., of CREC, Lanzhou, 730000, China)

Abstract：This paper intends to determine the fixed form of dam-board installed on earth embankment wind-break wall and to find the computational method for safe burial depth in wind-blown-sand with two phase flow in the case of the combined action of strong wind and sand. Numerical simulation software is employed to analyze the characteristics and rules of flow field around the dam-board through at different wind speeds. The stresses of heightened dam-board under the loads of wind and sand are calculated separately, and the support reaction is also computed. Finally, the approximate calculation method of burial depth of heighten dam-board in extreme condition is determined to provide some references and basis for safe operation and the design of sandy air prevention of railways.

Key words：Wind-break wall; Sand load; Wind load; Numerical simulation; Buried depth calculation

中图分类号：U216.41+3

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2015.01.004

文章编号：1004-2954(2015)01-0016-05

作者简介：朱文智(1990—)，男，硕士研究生，E-mail:zwz7895123@sina.com。

基金项目：国家自然科学基金(51268050)；国家青年科学基金(50908152)

收稿日期：2014-04-24