基于排队论的突发性事件中应用医疗救援小组的优选研究*

李 浩 宣绍伍

(武警警官学院 成都 610213)



基于排队论的突发性事件中应用医疗救援小组的优选研究*

李 浩 宣绍伍

(武警警官学院 成都 610213)

论文针对大规模突发性事件所带来的医疗问题进行了分析,提出了两种医疗方案,并运用排队轮模型对两种方案进行评价,得出结论。该方案有较好的实用性,而且简单易行,容易推广。

排队论; 医疗小组; 优选

Class Number O226

1 引言

建立突发性医疗救援小组新形势下武警部队建设势在必行的一个发展方向。然而针对当前形势和面对的多样化频繁化突发性事件,针对不同性质、规模突发性事件所带来的不同医疗问题,如何合理地使用我们新建立的医疗救援小组是当前一个迫在眉睫的问题。本节就主要针对常态、零散性突发性事件、大规模突发性事件合理安排运用救援小组进行了分析,并针对可能发生的大规模突发性事件进行了合理假设,在如何提高医疗小组救援效率的问题中采用多种排队讨论的方法对方案进行研究。

2 问题的引入

根据藏区大规模突发性事件的情况,假设两类伤员的到达分别服从于参数为λ1,λ2(λ2≥λ1>0)的Poisson流,将重伤伤员和轻伤伤员分别叫做1类B类伤员。为了提高医疗小组的医疗效率,在医疗救援的中心的战备预案中也将医疗小组分为了A、B两类医疗救援小组以便能够快速地投入救援工作。

本次大规模突发性事件发生后,藏区应急救援小组迅速收拢人员,将全部兵力、全部精力投入在处置突发性事件的救援工作中。医疗救援中心最短时间组建16支救援小组投入救援,分别为A类10组,B类6组。现在我们知道的情况是A类救援小组治疗A类、B类伤员分别要30min、25min；B类救援小组治疗A类、B类伤员分别要35min、40min。

现在要解决的问题是将电脑模拟泊松流(附件工作表1和2)给出了该次突发性事件中A类和B类伤员陆续到达某救援中心的时间。在保证每个伤员等待时间尽量不超过30min的条件下,给出最合理的A和B两类救援单元的救援策略,并对救援结果给出评价分析。

3 两种方案的分析

首先,我们将所有的伤员数目进行分析,得知B伤员的数目为177个,A伤员的数目为235个,而A类救援单元的数量是B类救援单元数量的1.5倍。我们采用分类医疗的方法(即A对A,B对B),两组按照各自的先来先救的原则。分类医疗流程图如图1所示。

图1 零散性突发性事件形势医疗救援小组工作分布

同样将表1数据代入此流程图计算单位时间(每110min为一个单位)A、B两类伤员的等待时间。

由表1可以看出该种策略虽然保住A类伤员的及时救援,但B类伤员的等待时间是线性增长趋势。若仅仅将伤员与救援单元的类型简单匹配(即A对A,B对B),会出现A类救援单元经常出现空时,而B类救援单元始终处于工作状态且无法完成救援任务。对于A类救援小组,工作强度虽小但工作效率很低；对于B类救援小组,会出处于高强度的治疗中。

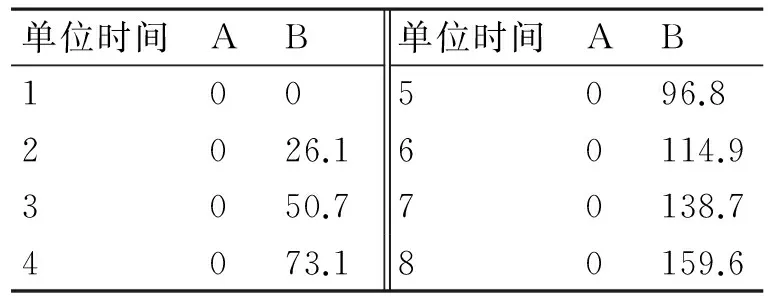
表1

此种情况是我们不想看见的,所以基于不发生伤员死亡和提高救援效率的原则制定以下方案:两类伤员分别为A类和B类,其中A类伤员具有高优先权,B类伤员具有低优先权。医疗救援单元分为A类和B类,当两类救援单元均处于可接收伤员的状态瞬间,只要系统上有排队等待的伤员,则立即对伤员进行A对应A,B对应B的治疗；当两类救援单元只有一个处于可接收伤员的状态瞬间,按照同类伤员先到先治疗的原则,不同类伤员优先权高的先治疗；当两类治疗对应均处于不可接收状态,等待队伍应按照优先权高的先排队。

A类伤员优先治疗流程图如图2所示。

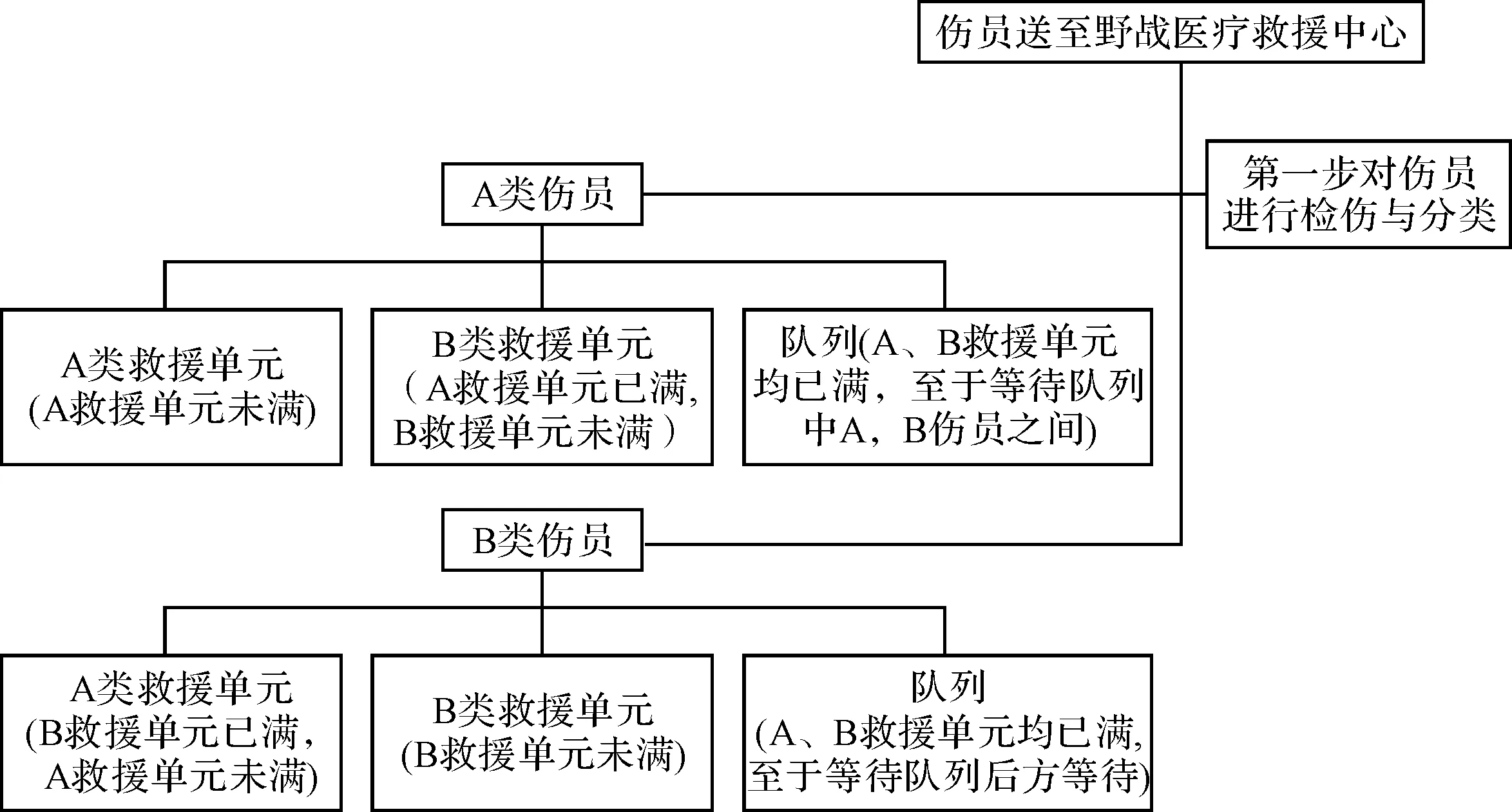
图2 优先治疗图

现将表1中数据代入计算出在排队高峰段为8:50～9:40；11:00～11:50；13:10～14:40；15:20～16:10；17:30～18:20；19:40～20:30这几个时间段A、B类伤员的平均等待时间如表2所示。

表2

如表2所示,进一步计算可以得出整个一天治疗A、B伤员的平均等待时间分别是1min,7min。

该种策略采用只要有医疗单元空闲立即送入伤员,所以对于A、B两类医疗单元的平均工作强度为λ/u=1.075。

4 基于排队论的数字分析

M/M/1模型[1～2]要求到达规律服从泊松过程,伤员到达参数为的负指数分布:

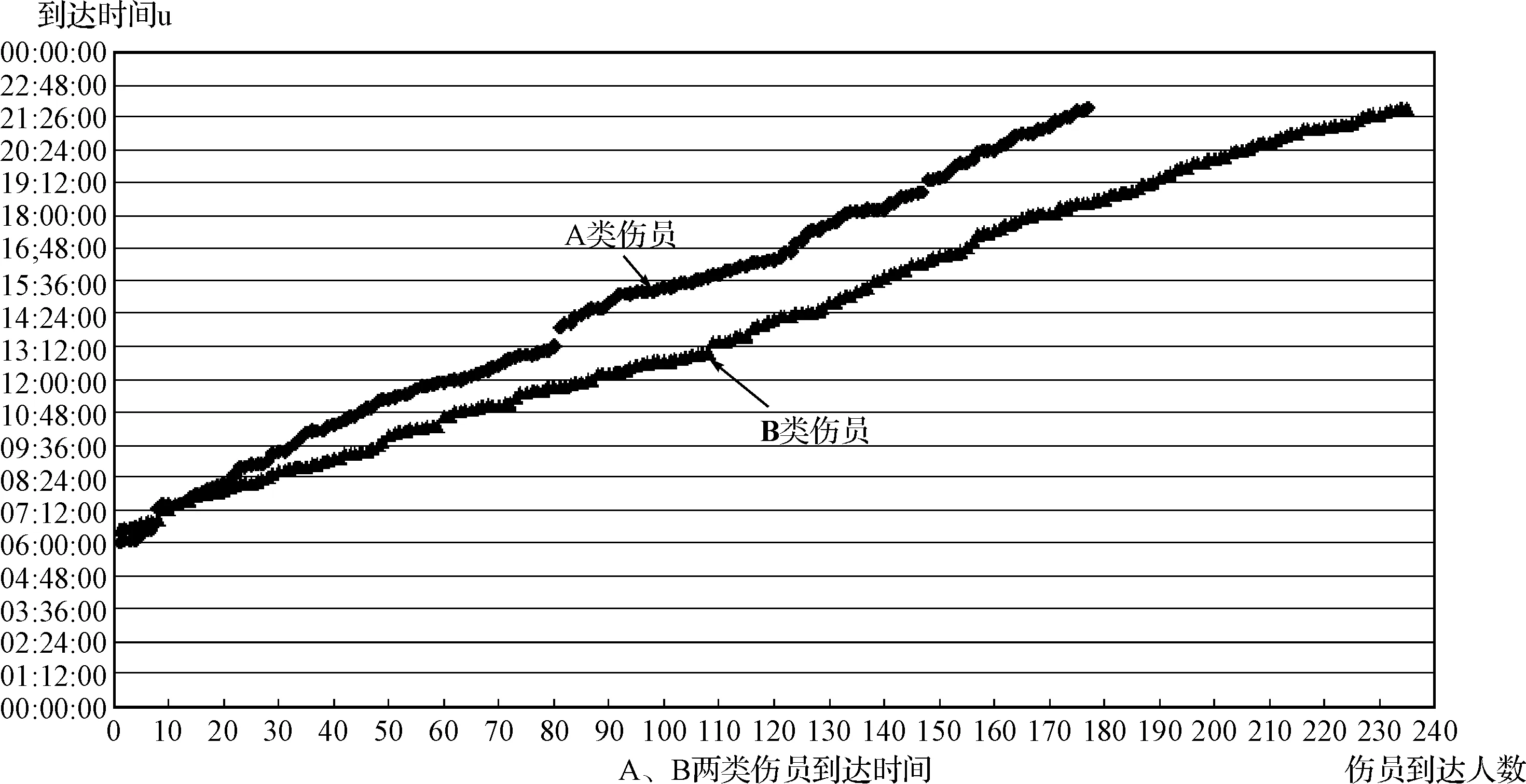
图3 A、B两类伤员到达时间

(1)

(2)

5 医疗救援小组运用方案的综合评价

下面是针对大规模突发性事件中两种不同的模拟策略,并带入题设中两类伤员到达的时间,进行流程图的推演。得到所要的评价值,通过对比分析,得出优化策略为A优先策略。该策略对于A、B两类伤员在紧急与非紧急的不同情况给出了,对A紧急给予了优先治疗权,充分考虑到了A类“重伤紧急组”伤员的黄金一小时,而对于B轻伤非紧急的平均等待时间也在良好的可控制范围内,不会出现一边排长队,一边治疗单元休息的情况。对于工作强度来讲,A、B两组治疗单元都做到了同时最优化。与之相比,另外一种策略——分组策略,虽然也充分保证了A紧急组的及时治疗,但B组等待时间成线性增长,带来了B组医疗排长队,A组医疗则是无人的资源浪费。在工作强度方面也极为不合理,B组工作强度与工作量明显高于A组。

表3为10:00～18:00的治疗救援情况: 1) 10:00～13:59:A、B两类伤员人数明显增加,但是B类伤员人数大于A类,所以在缓解B类救治单元工作强度的同时,必须考虑在完成A类救治单元前提下再考虑进行B救治单位的救治,但此举会导致B类伤员的堆积。 2) 13:00～17:59:在此段两类伤员的个数明显下降,可以把B适当的安排在A类救治单元,来缓解B类救治组的工作压力,以免出现堆积,造成死亡。

表3

6 结语

本文采用了专家评析法,比较符合解决可能发生问题的逻辑思维。通过专家的经验、实际的情况能够比较准确合理地得到结果。本文的医疗救援小组在大量伤员的医疗救援问题策略是:考虑情况全面,问题分析系统合理,采用方法理论充分,可加以发展,运用到抗震救灾、抗洪抢险等更大规模需要武警医疗救援部队的决策中。

[1] 王兴贵.基于排队论的银行排队问题研究[J].湘潭师范学院学报,2008(1):30-34.

[2] 高志华.基于排队论的防空作战效能评估[J].舰船电子工程,2012(8):45-49.

[3] 毛德耀.基于排队论的舰船装备维修保障模型[J].兵工自动化,2012(6):56-60.

[4] 潭乐祖.武警学院效能评估方法研究[J].火力指挥控制,2011(12):78-83.

[5] 胡贵安.一种新的炮兵装备维修资源优化配置模型[J].舰船电子工程,2010(6):65-70.

Optimization of Medical Rescue Team in Emergencies Based on Queuing Theory

LI Hao XUAN Shaowu

(Officers College of the CAPF, Chengdu 610213)

In this paper, large-scale emergencies caused by medical problems are analyzed, two medical programs are proposed, and the role of queuing theory model is used to evaluate the two programs. The program has good usability and simple, easy to promote.

queuing theory, the medical team, preferably

2014年7月11日,

2014年8月23日 基金项目:国家自然科学基金项目(70471031)资助。

李浩,男,硕士,讲师,研究方向:军事系统建模与优化决策。宣绍伍,男,研究方向:军事系统建模与优化决策。

O226

10.3969/j.issn1672-9730.2015.01.032