一种新的INS/LOG组合导航算法

高　薪，卞鸿巍，刘文超

(海军工程大学 导航工程系，湖北 武汉 430033)

一种新的INS/LOG组合导航算法

高薪，卞鸿巍，刘文超

(海军工程大学 导航工程系，湖北 武汉 430033)

摘要：针对电磁计程仪引入的海流速度可能会导致INS/LOG组合导航系统的卡尔曼滤波器输出发散问题，设计一种新的INS/LOG组合方式。以计程仪速度2次采样的差分值(即速度增量)作为系统观测量以抑制慢变海流的影响，采用基于延迟状态卡尔曼滤波算法，推导这种组合方式的观测方程，实现INS误差的最优估计。为抑制计程仪速度差分对其高频噪声的放大效应，采用巴特沃斯低通滤波器对其输出进行平滑处理。通过对3种INS/LOG组合方式的仿真比较，验证该算法的有效性。

关键词：组合导航；惯导；电磁计程仪；速度增量；延迟状态卡尔曼滤波

0引言

惯性导航系统(INS)的误差会随着时间积累，长时间工作后因超差而无法满足要求，因此须与其他导航设备组合才能得到精度更高的导航信息。目前，INS与GPS等卫星导航系统组合方法的研究较成熟，效果也较好。但卫星导航系统需依赖外界信息的支持，并且在水下导航场合无法使用。计程仪属于自主式导航装备，可为舰艇提供较高精度的速度信息，它可与惯导系统组成自主、隐蔽、可靠且精度较高的组合导航系统。

目前，得到广泛应用的计程仪与惯导的组合方案是通过设计阻尼网络[1]，引入计程仪的速度信息对惯导水正回路进行阻尼以抑制舒拉周期振荡。惯导的水正回路是典型的二阶临界稳定系统，在常值误差源激励下会产生舒拉周期形式的等幅振荡(无阻尼振荡)。而在陀螺随机漂移、加速度计随机误差的激励下，惯导系统的无阻尼振荡幅值会随着时间发散[2]，最终造成系统超差。采用经典控制理论设计的阻尼网络，可以改善水平回路的稳定特性，使舒拉和付科周期性震荡得到衰减。但这种方法只能抑制振荡性误差，对于常值或者随时间增长的误差量[1]，如经度误差随时间增长的部分没有抑制作用。

利用卡尔曼滤波器将惯导系统与计程仪进行信息融合，不仅可以获得与传统阻尼网络同样的阻尼效果[3]，还可以进一步提高系统的精度。目前，利用外部速度信息与惯导系统组合滤波的研究多是关于多普勒、声相关等绝对计程仪的，如文献[4]中建立了多普勒计程仪的误差特性方程，并使用多普勒计程仪来设计组合导航系统，有效提高了系统精度。目前，仍在大量使用的电磁计程仪本身具有较高的测速精度，然而由于电磁计程只能提供对水速度，海流速度会严重影响组合系统的精度。但海流在较短的时间内相对稳定，流速、流向基本不变。因此，若将计程仪的2次采样值进行差分，就可消除慢变海流的影响，得到较为准确的舰船对地速度增量。基于以上思想，本文以速度增量作为观测量，建立系统观测方程，并采用与之相应的基于延迟状态的卡尔曼滤波算法，建立了一种新的INS/LOG组合方式，以消除海流速度的影响，提高系统精度。

1状态方程的建立

惯导的陀螺和加速度计误差都可以用随机常数加上白噪声的形式表示[5-6]：

(1)

(2)

式中：εbi为陀螺常值漂移；▽Abi加速度计常值零偏；εwi为陀螺随机漂移；wi为加速度计随机误差(i=x,y,z)。将εbi和▽Abi列为状态量，则连同惯导7项误差量一起构成12维状态量：

X=[δφ,δλ,δVx,δVy,φx,φy,φz,▽Abx,▽Aby,

εbx,εby,εbz]T。

(3)

式中：δφ和δλ分别为纬度、经度误差；δVx和δVy分别为东向、北向速度误差；φx， φy， φz为平台失准角；▽Abx和▽Aby分别为东向、北向加速度计常值零偏；εbx,εby,εbz分别为东向、北向和天向陀螺常值漂移。则根据惯导误差方程可得状态方程为：

X)X(t)+W(t)。

(4)

其中状态传递矩阵F(t)可参考文献[7]，W(t)为系统噪声：

W(t)=[0,0,wx,wy,εwx,εwy,εwz,0,0,0,0,0]。

(5)

2观测方程的建立

2.1　观测量的选取

电磁计程仪的测量值为舰船相对海水的速度，因而电磁计程仪输出的速度值应为舰船对地真实速度、海流速度及计程仪误差的和：

Vj=Vr+Vf+δVj。

(6)

式中：Vj为计程仪测得的舰船对水速度；Vf为海流速度；Vr为舰船对地真实速度，δVj为计程仪测量误差。

海水流速一般小于2 kn，但有些海流的流速可达4~5 kn以上[8]。根据海洋学原理，海样是一个不可压缩的流场，海流的空间尺度大，一般具有数百甚至数千千米的流动范围。在较短的时间内海流相对稳定，流速、流向基本不变[8]，因此可认为采样时间较短时，计程仪速度的2次采样值中的海水流速不变。2次采样值差分可得：

ΔVj(k)=Vj(k)-Vj(k-1)=

Vr(k)+Vf(k)+δVj(k)-[Vr(k-1)+

Vf(k-1)+δVj(k-1)]=[Vr(k)-Vr(k-1)]+

[δVj(k)+δVj(k-1)]。

(7)

计程仪速度差分后，已消除了海流的影响，ΔVj(k)较真实地反映了载体在1个采样周期内的对地速度增量[Vr(k)-Vr(k-1)]。但式(7)含有的[δVj(k)+δVj(k-1)]项可能会“放大”计程仪噪声中的高频成分，因而需要设计低通滤波器，消除计程仪输出中的高频成分，ΔVj(k)才能准确表示舰艇的对地速度增量。

2.2　低通滤波器的设计

电磁计程仪测量误差主要由零位误差、刻度系数误差和随机误差组成。文献[6]对电磁计程仪误差进行了分析，并建立了电磁计程仪误差的数学模型，将计程仪误差分为常值误差，一阶马尔科夫过程和白噪声。在频域上计程仪噪声可分为低频部分和高频部分：

δVj=δVjL+δVjH。

(9)

式中：δVjL为计程仪误差的低频部分；δVjH为计程仪误差的高频部分。

巴特沃斯(Butterworth)滤波器是一种具有最大平坦响应的低通滤波器，在实际工程中应用广泛[9]。巴特沃斯低通滤波器的幅频特性为：

(10)

式中：n为滤波器阶数；ωb为低通滤波器截止频率。当阶次n增大时，滤波器的特性曲线会变得更加陡峭，其特性更接近理想的矩形幅频特性，低频信号的保真度越高。巴特沃斯低通滤波器的阶数n由下式求得：

(11)

式中：αs为阻带最小衰减；αp为通带最大衰减；ωb为通带截止频率。显然归一化后，λp=ωb/ωb=1，λs=ωs/ωb，其中ωs为阻带截止频率。

由上分析可知：阶数n越高，其幅频特性越好 ，低频检测信号保真度越高。因此。可尽量选择阶数较高的低通滤波器。设计低通数字滤波器的目的就是通过该滤波器获得所需的低频信号。为电磁计程仪的输出信号设计低通滤波器的目的是为了获取其 “直流”输出，故其截止频率应为0。当然，设计这种滤波器 ，不论在理论上还是在实践上，都相当困难。因此，本文的设计思想是归一化后的频率λs尽量小。

在船载条件下,大部分扰动频率都在1/15 Hz以上[11]，为得到较为准确的载体线运动信息，本文选择ωb=0.1 Hz，ωs=0.2 Hz，带通最大衰减为αp=3 dB，阻带最小衰减为αs=35 dB。则由式(11)可算出n=3，将ωb， αp， n代入下式：

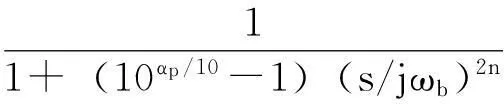
(12)

计算出滤波器3个极点分别为：

(13)

则可得巴特沃斯低通滤波器的传递函数为：

(14)

为验证低通滤波器效果，对上述滤波器进行仿真，结果如图1所示。由图中可看出，本文设计的巴特沃斯低通滤波器可有效抑制信号中的高频成分。

图1　巴特沃斯低通滤波器输出Fig.1　Result of Butterworth low pass filter

2.3　建立量测方程

由以上分析可知，计程仪2次采样值的差值可以较为准确地反映出舰船在采样周期内的对地速度增量。以计程仪速度差分得到的东、北向速度增量与惯导测得的东、北向速度增量的差值作为观测量：

(15)

式中：ΔVIx和ΔVIy分别为惯导测得的一个采样周期内东、北向速度增量：

(16)

将式(7)和式(16)式代入式(15)得：

H(k)X(k)+L(k)X(k-1)+Vj(k)。

(17)

上式即为含有延迟状态的观测方程，其中δvjx(k)和δvjy(k)分别为计程仪东北向速度差分后量测噪声。认为是白噪声，H(k)和L(k)分别为：

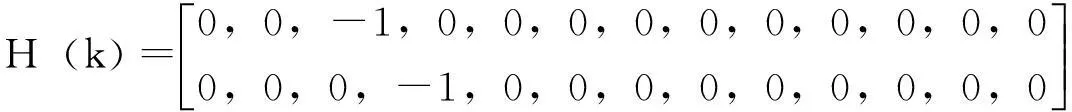
3延迟状态卡尔曼滤波算法

由于式(16)观测方程中含有延迟状态X(k-1)项，即K时刻的观测值与上一时刻的状态量有关。因此不能使用普通形式的卡尔曼滤波器，含有延迟状态量的观测方程可使用延迟状态卡尔曼滤波器[10]：

状态一步预测：

X^k/k-1=Φk,k-1X^k-1；

状态估计：

X^k=X^k/k-1+Kk(Zk-HkX^k/k-1-LkX^k-1)；

滤波增益：

一步预测均方误差：

估计均方误差：

其中：

本文采用输出校正的方式将计程仪与惯导系统进行组合，系统原理如图2所示。

图2　INS/LOG组合到导航系统原理图Fig.2　Schematic diagram of the INS/LOG intergraded system

4系统仿真

为验证本文方法的效果，在考虑海流影响的情况下，分别对平台式惯导与电磁计程仪3种不同组合方式在Simulink中进行仿真：模式1为传统的外速度水平阻尼方案；模式2为以计程仪速度值为观测量的普通卡尔曼滤波方案；模式3为本文提出的组合方案方案。

仿真条件为：假定舰船匀速直航，航速15 kn，航向45°；初始位置：φ0=30°，λ0=120°；初始平台角误差：φx=1′,φy=1′，航向误差φz=3′；加速度计常值零偏为100 μg，随机零偏为50 μg；陀螺常值漂移均为0.001°/h，随机漂移0.000 5°/h；电磁计程仪量测误差0.2 kn(看作白噪声)。计程仪速度值的采样周期和滤波周期都为10 s，仿真时间48 h。假定海流Vf由3部分组成：

Vf=Vs+Vc+Vw。

式中：Vs=sin[(1/24×3 600)t]是周期为24 h、峰值为0.3 kn的潮汐流(看作是时间的正弦函数)；Vc为1 kn恒定海流，Vw是强度为0.2 kn的随机海流，海水流向为45°。

仿真结果如图3~图5所示。

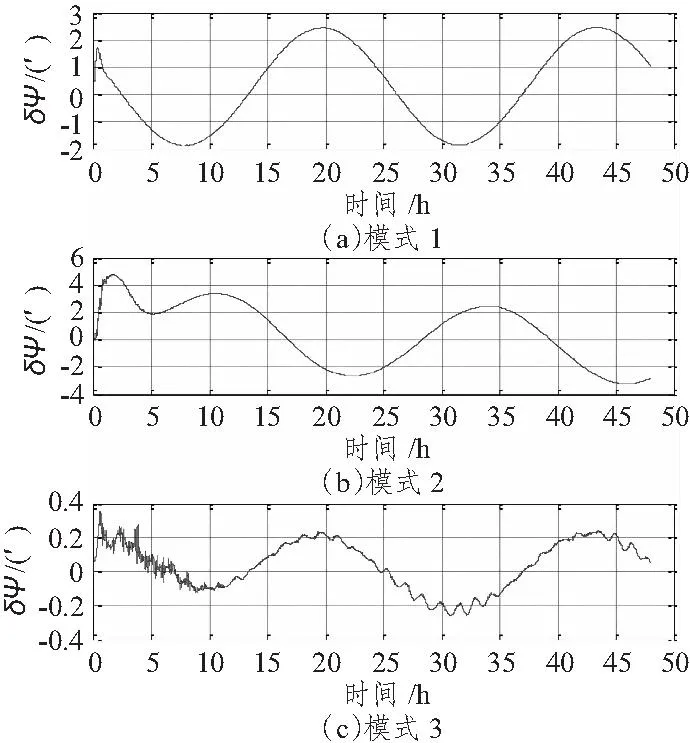
图3　系统纬度误差Fig.3　Latitude errors of the system

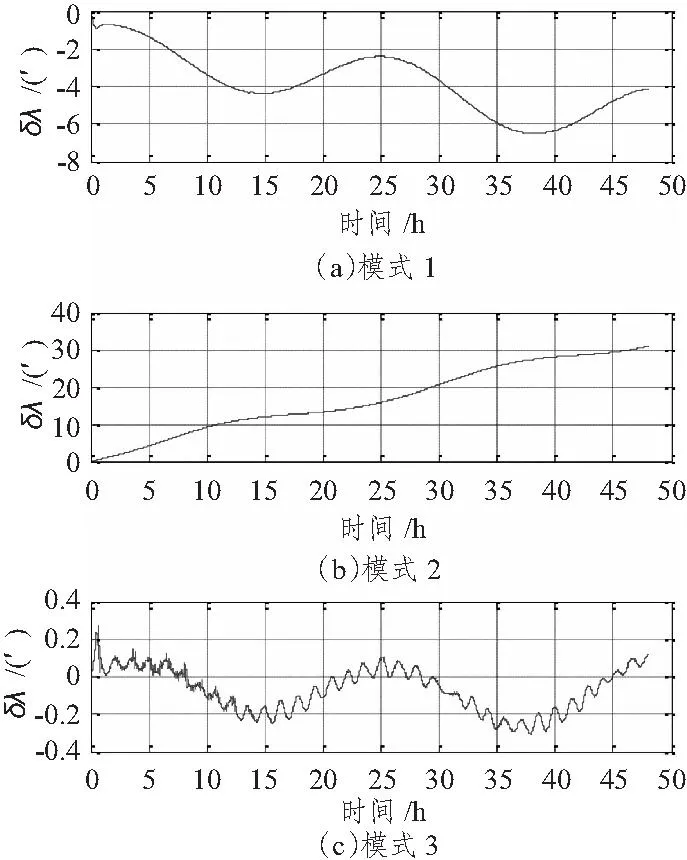
图4　系统经度误差Fig.4　Longitude errors of the system

图5　航向误差Fig.5　Heading errors of the system

由图可看出，组合模式1中的传统阻尼网络可以消除纬度舒拉震荡成分，纬度误差为地球周期震荡，峰值约为2′，经度误差在经过2 d以后发散到大约6′，航向误差也为地球周期震荡，并且含有常值误差，误差峰值约为3′；在组合模式2中，由于恒定海流及缓慢变化的潮汐流的影响，计程仪输出速度中含有较大常值海流成分，造成纬度误差缓慢发散，2 d后达到3′，经度误差则发散到了30′，航向误差最大值为2.8′，表明海流对模式2的精度影响较大；组合模式3由于消除了稳定海流的影响，位置误差精度较高，其中纬度误差控制在0.4′，经度误差抑制效果较明显，经过2 d后误差控制在0.3′以内，航向误差则控制在0.5′以内。

仿真结果表明，电磁计程仪引入的稳定海流速度误差对传统阻尼网络的精度影响不大；普通卡尔曼滤波器则由于海流影响，位置估计精度变差，特别是经度误差比传统外速度阻尼误差更大；模式3中采用速度增量为观测量，基本可以消除海流速度的影响，位置及航向精度均优于模式1和模式2。

5结语

为解决电磁计程仪引入的海流速度可能会导致INS/LOG组合导航系统精度发散的问题，本文提出了采用了计程仪2次采样的差分(即速度增量)为观测量，基于延迟状态卡尔曼滤波算法将惯导和计程仪数据进行信息融合。仿真结果证明本文方法可有抑制系统精度的发散，提高了系统精度。

参考文献：

[1]陈永冰，钟斌.惯性导航原理[M].北京：国防工业出版社，2007.

[2]查峰，许江宁，覃方君,等.捷联惯导系统内水平阻尼网络设计[J].兵工学报，2011，32(8)：997-1001.

ZHA Feng，XU Jiang-ning，QIN Fang-jun,et al.Damp Network design of horizontal loop in strapdown inertial navigation system[J]. Acta Armamen-Tarii， 2011，32(8)： 996-1001.

[3]BROWN R G，HWANG P Y C.Introduction for random signals and applied kalman filtering [M].New York：John Wiley & Sons，1997：255-276.

[4]李佩娟，徐晓苏， 张涛.信息融合技术在水下组合导航系统中的应用[J].中国惯性技术学报，2009，17(3)：344-349.

LI Pei-juan，XU Xiao-su，ZHANG Tao.Application of information fusion to integrated navigation system of underwater vehicle[J].Journal of Chinese Inertial Technology，2009，17(3)：344-349.

[5]秦永元，张洪钺，汪叔化.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，1998：286-301.

[6]汪凤林，蔡体菁，罗斌.速率方位惯性平台/GPS/计程仪组合导航系统仿真研究[J].中国惯性技术学报，2005，13(2)：35-40.

WANG Feng-lin，CAI Ti-jing，LUO Bin.Rate azimuth inerial platforn/GPS/log intergrated navigation system[J].Journal of Chinese Inertial Technology，2005，13(2)：35-40.

[7]卞鸿巍，李安，许江宁,等.现代信息融合技术在组合导航中的应用[M].北京：国防工业出版社，2010：100-102.

[8]郭亚娜.航海气象与海洋学[M].大连：大连海事出版社，2011：145-152.

[9]李钟慎.基于MATLAB设计巴特沃斯低通滤波器[J].信息技术，2003，27(3)：49-52.

LI Zhong-shen.The design of butterworth low-pass filter based on MATLAB[J].Information Technology，2003，27(3)：49-52.

[10]STANWAY M J.Dalayed-state sigma point Kalman filter for underwater navigation[C]//Autonomous Underwater Vehicles(AUV).IEEE，2010：1-9.

[11]WAN D，HUANG Y，REN T.Study on new kalman filter mechanization for initial alignment of INS in random rocking vehicles[C]//ΠΠStuttgart, West Germany，1989.

A new algorithm for INS/LOG integrated navigation system

GAO Xin,BIAN Hong-wei,LIU Wen-chao

(Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033,China)

Abstract：Since the measurement of electromagnetic LOG contain ocean current velocity, and this might cause the divergence of the Kalman filter of the INS/LOG integrated navigation system. A new INS/LOG integrated navigation system is designed, which base on the Delayed-state Kalman filter, twice sampling of LOG speed difference is adopted as its measurement variables (i.e. velocity increment) to restrain the error caused from the . The paper deduces the observation equation of this new integrated navigation system in detail and applies this INS/LOG integrated navigation system to estimate INS error. To restrain amplification effect on the high frequency noise, butterworth low pass filter is introduced to smooth the LOG data. Comparing the perfomance of this new INS/LOG system integrated system with that of other two INS/LOG system, and the simulation result verified the effectiveness of the proposed algorithm.

Key words：intergraded navigation system; INS; electromagnetic LOG; velocity increment; delayed-state kalman filter

作者简介：高薪(1982-)，男，博士研究生，从事导航制导与控制研究。

基金项目：航空科学基金资助项目(920120816001)

收稿日期：2013-11-06； 修回日期： 2013-12-12

文章编号：1672-7649(2015)02-0053-05

doi：10.3404/j.issn.1672-7649.2015.02.011

中图分类号：U666.1

文献标识码：A