基于SST k-ω湍流模型的二维圆柱涡激振动数值仿真计算

李　骏，李　威

(华中科技大学 船舶与海洋工程学院，湖北 武汉 430074)

基于SSTk-ω湍流模型的二维圆柱涡激振动数值仿真计算

李骏，李威

(华中科技大学 船舶与海洋工程学院，湖北 武汉 430074)

摘要：随着海洋工程逐渐向深海发展，广泛使用的柔性立管因为高频振动很容易受到严重的损伤。因此对于这类细长柔性结构的涡激振动(VIV)研究是当今的一个热点，同时随着计算机的快速发展，CFD (计算流体力学) 技术成为研究涡激振动问题不可或缺的一种方法。本文采用雷诺平均纳维尔-斯托克斯(RANS)方程，并结合SST k-ω 湍流模型，研究低质量比弹性支撑刚性圆柱体的涡激振动问题。从振幅响应、频率响应、3个响应分支的水动力性能、尾涡模式等方面和Williamson相关实验作对比。结果表明，SST k-ω 湍流模型能够有效准确地模拟圆柱绕流的涡激振动。本文丰富了海洋工程的理论研究，为柔性立管的实际应用提供了一定的理论指导。

关键词：涡激振动；SST k-ω湍流模型；立管

0引言

很多工程领域中都会涉及到涡激振动 (VIV) 问题，在海洋管道、立管或者其他水下结构中尤其明显。近年来随着柔性材料的广泛应用，产生了大量关于低质量比的圆柱涡激振动研究成果[1-3]。

对于弹性支撑的刚性圆柱在自由来流下的横向涡激振动研究，Williamson 的团队通过一系列实验[4-7]为这项研究做出了巨大贡献。他们的实验结果可以概括成以下3点：一是对于低质量比的弹性支撑刚性圆柱在横向振动方向会产生3种明显的振幅响应分支，分别是初始分支、上端分支和下端分支；二是在不同的响应分支，尾涡的脱落模式也各有不同；三是在相邻响应分支的过渡点会伴随着相应的相位角突变。

借助CFD (计算流体力学) 模拟涡激振动时，大致有3个方法处理N-S(纳维尔-斯托克斯) 方程，分别是雷诺平均纳维-斯托克斯(RANS)、直接数值模拟(DNS)和大涡模拟(LES)。相比其他2种方法，RANS方法已经足够成熟，并且可以在较短的计算时间内得到相当精确的结果。Pan和Cui[8]在Khalak和Williamson实验基础上使用RANS方法来模拟二维数值模型。他们发现在涡脱模式和不同分支之间的转变方面与实验结果基本一致，但是模拟获得的响应振幅远低于实验结果，尤其是最大响应振幅的时间点只有1个，这与实验结果完全不一致。

本文参照Khalak 和 Williamson 的实验模型，定义圆柱的质量比m*=2.4 ，质量阻尼比 m*ξ=0.013；折合速度U*=Uinlet/(fnD)从2.0增加13.9；相应的雷诺数从1 700增加到11 600。采用SSTk-ω湍流模型研究弹性支撑刚性圆柱在自由来流下的横向涡激振动问题，为评判该模型在这一研究的正确性，所有数值仿真结果都将与Khalak 和 Williamson 的相关实验结果作对比。

1计算模型

1.1　控制方程

对于非定常不可压缩流体，其RANS方程可以写作：

(1)

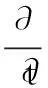
(2)

(3)

式中：涡流粘度μt由湍流模型给出；δij为克罗内克函数；k为湍流动能。

(4)

同时，结合“切片理论”，可将计算模型简化至二维：首先将结构看成大量的沿立管轴向的切片，每个切片都可以当做1个弹性支撑的刚性圆柱，并且等效于只有1个自由度的线性弹簧质量阻尼系统。简化过程如图1所示。

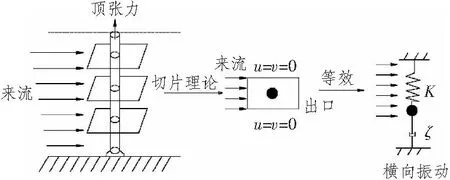
图1　三维立管简化过程Fig.1　The simplification process of a 3D riser

因此，圆柱在其横向方向的无量纲运动方程为：

(5)

式中：U*为折合速度；ζ为系统结构的阻尼比；m*为质量比；y为无量纲的横向位移；CL为横向的升力系数。

比较两组治疗前后呼吸困难程度评分（MMRC）、6 min步行距离（6MWD）、肺功能状态（FEV1预计值）等。

当圆柱涡激振动进入“锁定区域”，尾涡的涡脱频率与圆柱振动频率完全相同，此时圆柱的位移为：

y=A*sin(ωext)，

(6)

CL=CL0sin(ωext+φ)，

(7)

CL=CLvcos(ωext)+CLa[-sin(ωext)]，

(8)

CLv=CL0sinφ,CLa=-CL0cosφ，

(9)

φ=arctan(-CLv/CLa)。

(10)

式中：CL0，CLv及CLa分别为升力系数的振幅及它在速度方向与加速度方向上的分量；ωex为圆柱振动圆频率；φ为升力系数和响应位移之间的相位角。

根据Parkinson[9]的研究，响应振幅比(A*=Ymax/D)和频率比(f*=fex/fn)为

(11)

(12)

因此，一旦得到了响应振幅比和频率比，就可通过上面2个方程反推得到CLv和CLa，以及相位角φ。

此外，根据Lighthill[10]的研究，圆柱体上的总流体力F可以分解为附加质量力Fpotential和旋涡力Fvortex。同样，将上述力无量纲化后可得到：

Cvortex=CL0-Cpotential，

(13)

其中，

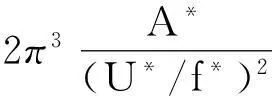
(14)

类似地，相应的无量纲运动方程还可以表示为：

(15)

式中：ma为圆柱的附加质量；ζ′为包含了附加质量系统结构的阻尼比；φvortex为旋涡升力系数与响应位移之间的相位角，可通过之前提到的相似方法求解得到。

采用Newmar k-β方法求解圆柱的横向振动响应位移，同时通过求解二维的RANS方程获得相应的流体力系数。

1.2　网格划分及边界条件

图2(a)为仿真模型的计算域，圆柱直径为D，计算域是一个宽为20D和长为30D的矩形。来流的边界条件在圆柱体中心左边10D的位置处，计算域右端则是流动出口边界。对称边界则分别在圆柱体上下10D的位置处，无滑移边界则是在圆柱体表面处。图2(b)为计算模型的网格划分，采用混合网格划分方式，由小及大的网格分布不仅可以减少仿真计算时间，并且可以得到更精确的计算结果。圆柱周围较密的网格可以精确模拟流动的尾涡情况。对于任意的折合速度，圆柱体外的第一圈网格始终划分在y+≤0.5的范围内。

图2　计算域和网格模型Fig.2　Computational field and grid model

2结果与分析

采用SSTk-ω湍流模型模拟弹性支撑的刚性圆柱体的涡激振动问题。需要指出的是，在流体域的仿真计算过程中，无量纲时间步U∞Δt/D=0.005 。同时以二阶隐式时间离散和二阶迎风空间离散格式对控制方程进行离散，并采用Simplec算法耦合求解平均速度场合压力场；而针对结构域的计算，则是通过对Fluent进行二次开发完成，即通过Fluent的用户自定义函数 (UDF), 在C语言环境下编写求解结构动力学运动方程的程序，来求解圆柱的振动响应；同时，结构变形引起的流场网格变化通过Fluent的动网格模型完成。

2.1　圆柱振动响应幅值比A*及频率比f*

在对圆柱涡激振动的研究中，圆柱的响应振幅比和频率比始终是最关注的2个因素。图3给出了用SSTk-ω湍流模型计算得到的振幅比和频率比分别与实验结果的对比(本文实验结果数值全部以空心圆点表示)。

从图3(a)可以看出，SSTk-ω模型成功计算出3种响应分支。在折合速度U*=3.5的时候，原始分支向上端分支转变；当折合速度U*=5.2时，出现下端分支。在上端分支中振幅达到最大值0.747，而在下端分支中振幅最大值0.642 ；当折合速度U*=11.0的时候，圆柱体的响应位移又回落到一个很小的数值，表明此时圆柱已进入了“涡脱区域”。

图3　不同折合速度下的最大振幅及振动频率(m*=2.4)Fig.3　Amplitude and frequency responses as a function of　reduced velocity (m*=2.4)

图3(b)给出了不同折速下对应的响应频率比，在锁定区内部，圆柱体的实际振动频率fex与固定圆柱体的泄涡频率fst分离，同时频率比稳定在1.15附近，而在解锁区，圆柱体的实际振动频率fex与固定圆柱体的涡脱频率fst相同，这与前人的实验结果大致相同。

2.2　圆柱尾涡涡脱模式

Govardhan和Williamson的研究结果[11]表明，圆柱涡激振动的不同响应分支对应的尾涡泄涡模式也各不相同：初始分支对应的泄涡是2S模式(即在一个涡脱周期内有2个单独的尾涡形成)，而在上端分支和下端分支对应的涡脱都是2P模式(即在一个涡脱周期内有2对尾涡形成)，不同的是上端分支中2对涡的涡强大致相等，而下端分支中第2个涡强度较第1个涡强度更小。图4所示为U*=3.0，4.8和7.3时一个泄涡周期内涡量变化的等值线图。

折速U*=3.0时，位于初始分支。尾涡泄放并不同于经典的卡门涡街(2S模式)，而更像是P+S模式(每个涡脱周期中从圆柱一侧泄放出2对涡，而在另一侧泄放出1个单涡)。

折速U*=4.8时，位于上端分支。从图4(b)可知,仿真模拟的泄涡模式是一个典型的2P涡脱模式，并与Williamson的实验结果完全吻合。

图4　一个涡脱周期内的涡量等值线图Fig.4　Vorticity magnitude contours within a vortex　shedding period

但在下端分支，SSTk-ω湍流模型的模拟结果似乎也不是2P模式，这说明泄涡模式还与圆柱的振动形式有关。采用SSTk-ω湍流模型成功模拟出2P模式，这是由于SSTk-ω湍流模型的湍流粘度计算中考虑到了湍流切应力的传播，而从可以有效的模拟流动分离。

2.3　流体力系数和相位角

如前所述，一旦圆柱的响应振幅比A*和频率比f*的值已知，就可以通过相关方程求得总升力系数CL，漩涡力系数Cvortex，以及对应的总相位角φ和涡相角φvortex。图5给出了相应的流体力系数和对应的相位角随折合速度的变化关系。

图5　不同折合速度下的升力系数和相位角(m*=2.4)Fig.5　Force and phase angle variations with U*(m*=2.4)

从图中可看出，在初始分支中涡相位角φvortex接近0°，表明漩涡力系数Cvortex和附加质量力系数Cpotential同相，因此总升力系数CL值很大。在上端分支，尽管涡相位角φvortex接近180°导致Cvortex和Cpotential异相，但由于圆柱振幅很大，因此Cpotential很大，且远远超过了Cvortex的值，所以此时CL值也较大。但在下端分支，Cvortex和Cpotential大小相当且异相，故升力系数CL变得相当小。此外，在初始分支过渡到上端分支处，由于φvortex发生突变，因此泄涡模式发生变化，由2S模式变为2P模式；而在上端分支过渡到下端分支时，φvortex并没有发生突变，因此泄涡模式也并未发生变化，依然保持在2P模式，这说明φvortex是否发生突变是评判泄涡模式是否发生变化的标准。

3结语

本文基于雷诺平均纳维-斯托克斯(RANS)方程, 研究了低质量比m*=2.4时的圆柱横向涡激振动问题，采用SSTk-ω湍流模型求解RANS方程，较好地再现了实验中的很多现象。

1)圆柱横向振动上端分支最大响应幅值为0.747，略小于实验值，可能原因是实际实验模型向二维的简化,而在频率响应计算中，圆柱锁定区的频率比稳定在1.15附近，与实验值较为接近。

2)SSTk-ω湍流模型成功模拟出了处于上端分支的2P涡脱模式，这得益于该模型在计算湍流粘度中考虑到了湍流切应力的传播，能有效模拟流动分离。

3)在初始分支向上端分支的过渡中，涡相角φvortex发生突变，且尾涡的泄涡模式也发生改变，由2S模式变为2P模式；而在上端分支过渡到下端分支时φvortex并没有发生突变，涡脱模式也未变化，说明φvortex是否发生突变是评判泄涡模式是否发生变化的标准。

从上面的分析可看出，无论是振幅响应和频率响应的计算，还是对升力系数和相位角的分析，SSTk-ω湍流模型的模拟结果较接近于真实的物理现象，并且采用SSTk-ω湍流模型成功地模拟出了2P模式，这些结论不仅为今后的数值模拟工作提供

借鉴，而且还为进一步的实验和理论研究提供了参考。

参考文献：

[1]BEARMAN P W.Circular cylinder wakes and vortex-induced vibrations[J].Journal of Fluids and Structures,2011(27):648-658.

[2]CATALANO P,WANG M,IACCARINO G.Numerical simulation of the flow around a circular cylinder at high Reynolds numbers[J].International Journal of Heat and Fluid Flow,2003(24)：463-469.

[3]GAO D M F,MINGHAM C G.Numerical and experimental investigation of turbulent flow around a vertical circular cylinder[C]//20th International Offshore and Offshore and Polar Engineering Conference Proceedings,2010：639-643.

[4]KHALAK A,WILLIAMSON C H K.Dynamics of a hydr-oelastic cylinder with very low mass and damping[J].Journal of Fluids and Structures,1996(10)：455-472.

[5]WILLIAMSON C H K.Advances in our understanding of vortex dynamics in bluff body wakes[J].Journal of Wind Engineering and Industrial Aerodynamics,1997:3-32.

[6]KHALAK A,WILLIAMSON C H K.Motions, forces and mode transitions in vortex dynamics in bluff body wakes[J].Journal of Wind Engineering and Industrial Aerodynamics,1999(13)：813-851.

[7]GOVARDHAN R,WILLIAMSON C H K.Modes of vortex formation and frequency response of a freely vibrating cylinder[J].Journal of Fluid Mechanics,2000：85-130.

[8]PAN Z Y,CUI W C,MIAO Q M.Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code[J].Journal of Fluids and Structures,2007(23):23-37.

[9]PARKINSON G V.Mathematical models of flow-induced vibrations of bluff bodies[J].Flow-Induced Structural Vibrations,1974:81-127.

[10]LIGHTHILL J.Fundamentals concerning wave loading on offshore structures[J].Journal of Fluid Mechanics,1986：667-681.

[11]GOVARDHAN R,WILLIAMSON C H K.Mean and fluctuating velocity fields in the wake of a freely-vibrating cylinder[J].Journal of Fluid and Structures,2000(15)：85-130.

Numerical simulation of vortex-induced vibration of a two-dimensional circularcylinder based on the SSTk-ωturbulent model

LI Jun1，LI Wei1,2

(Department of Naval Architecture and Ocean Engineering, Huazhong University of Science and

Technology,Wuhan 430074,China)

Abstract：Due to the great damage to widely utilized flexible structures in ocean engineering, vortex-induced vibration (VIV) of such long flexible marine structures is still a hot issue that needs more theoretical research, and CFD techniques become gradually indispensable to study the VIV problem. In this paper, two-dimensional Reynolds-averaged Navier-Stokes (RANS) equations are adopted to investigate transverse VIV of elastically mounted rigid cylinder with low mass-damping, and SST k-ω turbulent model is applied to solve the RANS equations. By comparing the cylinder displacement response, frequency response, vortex shedding modes of three different response branches, and other hydrodynamic coefficients with the previous research in detail, the numerical results indicate that SST k-ω model is invalid and accurate for VIV of the elastically mounted rigid cylinder. This investigation provides theoretical evidence for the numerical simulation of VIV of marine riser in engineering application.

Key words：vortex-induced vibration (VIV); SST k-ω turbulent model;riser

作者简介：李骏( 1990 - ) ，男，硕士研究生，主要从事海洋结构物设计与制造工作。

收稿日期：2014-03-05； 修回日期： 2014-07-07

文章编号：1672-7649(2015)02-0030-05

doi：10.3404/j.issn.1672-7649.2015.02.006

中图分类号：U661.44

文献标识码：A