缓波形钢悬链立管时域动力与疲劳分析

，，，

(1.中国船舶工业集团第七〇八研究所，上海 200000； 2.哈尔滨工程大学 船舶工程学院 深海工程技术研究中心，哈尔滨 150001)

缓波形钢悬链立管在工程中的应用近年来刚刚起步[1]，为保证立管工作的安全性，进行完整的设计分析尤为重要。此外，由于浮力材的添加，立管构型更加复杂，此前对不同构型的钢悬链立管计算分析发现，不同构型的立管强度与疲劳等性能有较大的不同。这表明具有较复杂构型的缓波形钢悬链立管的强度与疲劳等特性将表现出不确定性，其相比于简单钢悬链立管在性能上的具体变化也需要在设计分析中重点考虑。因此，为保证缓波形钢悬链立管工作的安全性并系统研究其相对于简单钢悬链立管的性能变化，基于悬链线法、集中质量法及S-N曲线法对缓波形钢悬链立管进行强度与疲劳等特性分析。采用OrcaFlex软件在时域范围内对简单钢悬链立管以及缓波形钢悬链立管进行计算对比分析，包括立管静态特性、动态特性、强度、疲劳等方面，探讨缓波形钢悬链立管整体特性及优势，并采用控制变量的方法分析不同设计参数对缓波形立管整体强度和疲劳特性的影响。

1 钢悬链立管动力分析方法

1.1 立管力学模型

管线分析采用的模型为集中质量模型，该方法计算速度较快，易收敛。

管线的时域动力方程表达式为[5]

(1)

式中：y为各节点位移；M为管线集中质量矩阵；B为阻尼矩阵；K为刚度矩阵；F(t)为管线所受外力，包括流体力、重力、管土接触力，对于缓波形立管，还包括浮力材产生的浮力等。

海洋立管在海洋环境中受到的海流、波浪等流体力常用半经验的广义莫里森方程计算[6]。管线切片ds所受流体力可以表示为

(2)

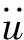
对海床的模拟采用线性无质量弹簧，当立管与海床相接触时，每个节点受到的海床垂向作用力为两侧单元受力之和的一半，可表示为

(3)

式中：ksb为土体刚度；Asbi为单元i与海床的接触面积，Asbi=Dli；i为节点两侧单元；dsb为立管中心渗入海床的深度，dsb=(D/2)-y。

1.2 疲劳分析方法

工程结构的疲劳分析一般采用两种方法：S-N曲线法和断裂力学法[7-8]。这里采用S-N曲线法进行疲劳分析。

S-N曲线描述了疲劳强度S和截止材料破坏时的应力循环次数N之间的关系。若在固定应力幅值S的循环作用下，将结构达到疲劳破坏所经历的循环次数记为N，则S-N曲线表达式为

N=aS-m

(4)

式中:a和m为材料参数，在试验过程中获得。对表达式两侧取对数，其形式近似为一条直线

lgN=lga-mlgS

(5)

应力幅值S需要经过壁厚纠正因子和应力集中系数的修正，即

(6)

式中：S0为公称应力幅；SCF为应力集中系数；tref为参考壁厚；k为壁厚指数。对于S-N曲线的选取，已有大量的工程经验，可查询相关规范选取合适的S-N曲线。

2 立管模型与环境载荷

2.1 立管参数

选取相同尺寸的缓波形钢悬链立管和简单钢悬链立管进行对比，具体参数见表1、2。

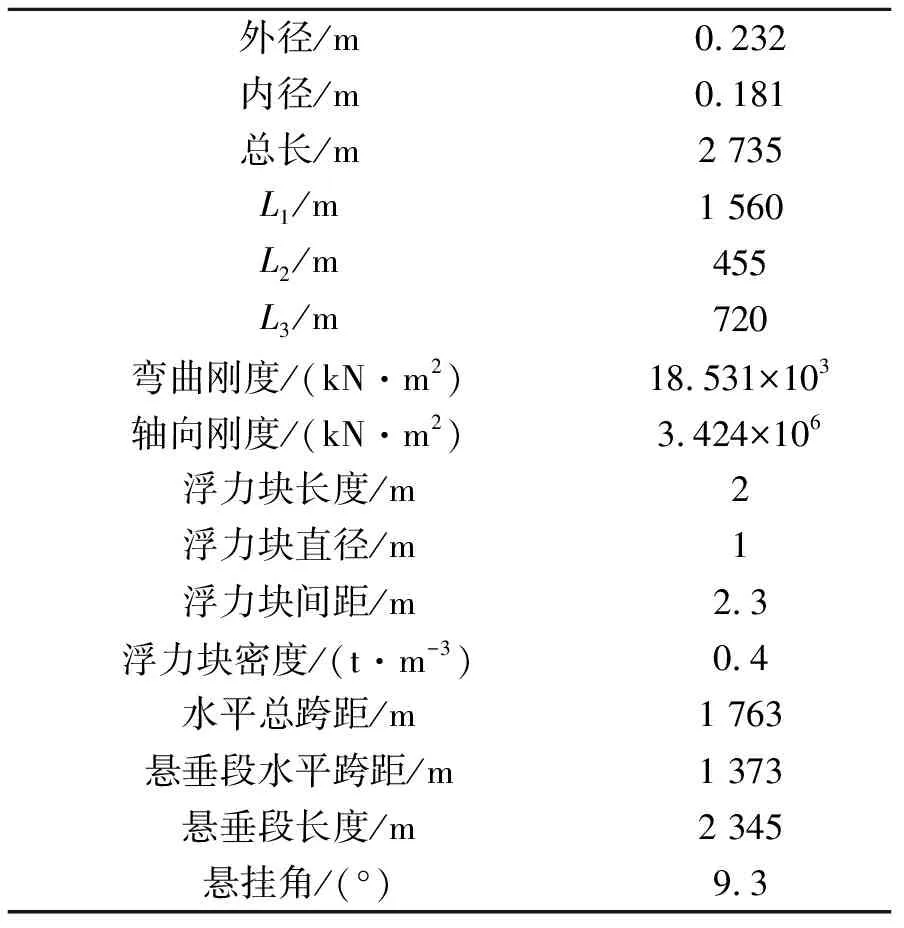
表1 缓波形钢悬链立管参数

表2 简单悬链线参数

2.2 平台参数

在对缓波形立管性能的分析中，采用半潜平台作为浮体，主要尺寸参数见表3。

2.3 强度分析环境参数

风浪流参数见表4、表5。

2.4 疲劳分析环境参数

浪致疲劳分析的波浪统计参数见表6。

表3 半潜平台主要参数

表4 波浪参数

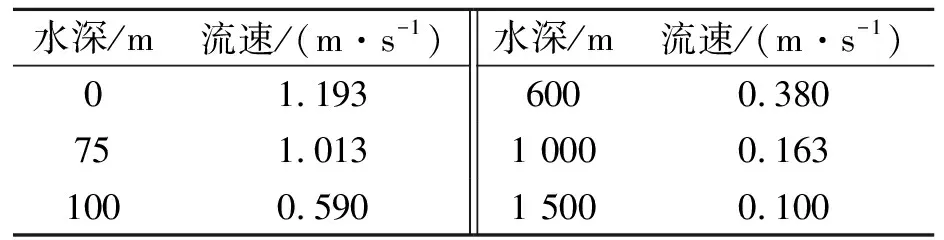
表5 洋流极限流速 m/s

表6 长期波浪分布统计表

3 立管动态运动与强度分析

3.1 静态分析

在对比分析缓波形与简单钢悬链立管的动态特性之前，先简要分析其静态特性。在OrcaFlex软件中利用悬链线法计算得到了2种立管的静态构型、张力、弯曲和应力特性曲线，见图1。

可以发现缓波形立管通过在立管中部添加浮力材，实现中部的凸起，这与简单悬链线立管显著不同。通过对比有效张力，发现缓波形立管顶部张力比悬链线型小很多，这是由于缓波形立管的顶部只需支撑顶部到波谷段立管的湿重，因此，在由于水深、管径等因素造成的立管顶部张力过大时，可采用缓波构型以减小平台的负荷。另外，立管弯矩与其曲率直接相关，相比悬链线构型，缓波形立管弯矩更大，这与浮力材布置密切相关。缓波形立管的顶部最大等效应力比悬链线构型小，为198.97 MPa，而简单悬链线立管最大等效应力为211.02 MPa，由此可见，缓波构型可以缓解立管顶部应力节的应力水平。

3.2 整体动态分析

在静态分析的基础上对缓波形钢悬链立管与简单钢悬链立管进行时域动态分析，得到立管有效张力、弯矩和等效应力的最大值、最小值和平均值，见图2～4。

对于缓波形立管，管线顶部的有效张力、弯矩和应力水平都有显著变化；浮力材部分运动幅值较大，该处由于浮力材的添加，所受流体力比较大，通过图3和图4可以看出，浮力材部分弯矩以及等效应力变化比较剧烈；但缓波形立管触地点位于沿管长2 340 m左右，触地点的有效张力、弯矩以及等效应力变化很小。

触地点位于沿管长1 780 m左右，该处有效张力、弯矩和等效应力变化剧烈，与缓波形立管形成鲜明对比，因此，缓波形钢悬链立管能够对触地区域形成保护，使平台运动对触地区域的影响有所减小，同时减小立管顶部的动态载荷与应力。

立管在平台慢漂运动下不同位置处的构型见图5。可以发现在触地点附近，缓波构型的变化幅值比简单悬链线型小很多，缓波构型在平台慢漂作用下可以产生一定程度的伸缩，使触地点得到保护，对平台慢漂的适应性更好。

3.3 不同构型立管的强度特性

对于缓波形钢悬链立管，其浮力材的参数，主要包括浮力材段位置和长度对立管的整体性能具有一定的影响。

将缓波形立管第一段长度，即立管从平台处至浮力材起始处的长度设为1 265 m、1 465 m和1 665 m，计算结果见图6。

由图6可见，随着第一段立管长度的增加，立管顶部产生更大的有效张力；随着浮力材位置降低，波形变缓，触地点之前的悬链线变短，使得浮力材与第三段交接处的有效张力减小；波形变缓使得立管各处曲率减小，立管弯矩变小，而顶部弯矩变化不大。立管等效应力的变化与有效张力和弯矩的变化紧密相关，在立管顶部到构型波谷之前，浮力材位置的降低使应力变大；在构型波谷之后，波形变缓导致的弯矩减小，使得等效应力随之减小。

浮力材长度分别为350 m、455 m和550 m的动态响应计算结果见图7。

可以发现随着浮力材长度的增加，使其悬跨段长度和跨距变长，构型波峰位置升高，波形变大，波谷和触地点处弯曲程度有所增强。立管的顶部张力随浮力材段的长度的增加有所减小，并使浮力材段末端的有效张力增加，并且峰值后移。对于立管的弯矩和等效应力，发现单纯地增加浮力材的长度，不能改善其弯曲性能，对应力极值的影响也较小，只是使波形更大，立管更长。

总之，通过调节浮力材的位置，能够显著改变立管顶部、浮力材段以及触地点的强度水平；调节浮力材的长度能够改变波形的大小，但对强度水平影响较小。

4 缓波形立管整体疲劳特性分析

4.1 缓波形与简单悬链线形疲劳对比分析

缓波形钢悬链立管与简单悬链线立管的疲劳性能计算工况为模拟时间1 200 s。为了使结果更具可比性，立管的网格划分尽量一致，在触地点附近的网格密度相同，疲劳寿命分布见图8。

缓波形钢悬链立管的疲劳危险点主要位于立管顶部应力节处、浮力材段和触地点。简单悬链线构型的立管，其疲劳危险点是顶部应力节处和触地点处，并且触地点的疲劳损伤尤为明显。触地点附近，简单悬链线立管疲劳寿命为44.86年，缓波构型立管疲劳寿命为388.65年，相比之下，缓波构型的疲劳寿命是简单悬链线构型的将近9倍；在顶部应力节附近，简单悬链线构型立管疲劳寿命为2 345.01年，缓波构型疲劳寿命为3 355.09年，缓波构型在顶部应力节附近的疲劳性能也有很大提升。可见，缓波构型大大减小了平台运动对触地点的影响，使得触地点疲劳寿命大幅提升，同时顶部应力节附近的疲劳性能提高。

4.2 缓波形钢悬链立管疲劳损伤特性

对立管损伤影响最大的5个工况下的总体疲劳损伤和触地点处的疲劳损伤见图9。

由图9a)可见，随着有义波高的增加，船体运动对立管顶部造成的疲劳损伤越明显，这是因为应力节直接与船体相连，船体运动的剧烈程度对立管顶部的疲劳影响更加明显。由图9b)可见，有义波高为2.5 m的工况造成的触地点疲劳损伤最大，在触地点附近的20 m范围内，疲劳损伤极其明显，而两侧疲劳损伤很小，如果该处的疲劳寿命仍然不满足要求，可以采取局部加厚等方式提高疲劳性能。

5 结论

1)缓波形钢悬链立管有4个应力高点，分别为立管顶部应力节下端，线性波谷、波峰和触地点；疲劳危险点有3个，分别为立管顶部应力节下端、浮力材段和触地点。在缓波形钢悬链立管设计时，需重点考虑这些危险点处的强度与疲劳，保证其在安全范围以内。

2)缓波形立管相对于简单悬链线立管的优势具体体现在动态运动、受力及疲劳三方面。缓波形立管在对平台运动以及慢漂具有更好的适应性，但其侧向位移较大，应防止立管干涉的发生；并且其顶部张力和应力较小，其顶部以及触地点区域的疲劳性能得到显著改善，具有更好的强度与疲劳安全性，可以更好地满足工程与规范要求。

3)立管浮力材段的位置、长度对缓波形立管整体强度有不同程度的影响，在设计时应谨慎选取。后续的工作可以针对更多的参数进行强度与疲劳敏感性分析，并采取相应的方法对各参数进行优化，以进一步提升缓波形立管的安全性能，增加其工程适用范围。

[1] 徐显明,朱克强,姬芬芬,等.转塔式系泊FPSO中的缓波型立管水动力分析[J].中国航海,2016,39(4):71-75.

[2] WU M, HUANG K. The comparison of various SCR configurations for bow turret moored FPSO in west africa[C]. The Seventeenth International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers,2007.

[3] FOYT E, GRIFFIN C, CAMPBELL M, et al. Weight Optimized SCR: Enabling Technology for Turret Moored FPSO Developments[C].ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers,2007:31-39.

[4] YUE B, WALTERS D, YU W, et al. Lazy wave SCR on turret moored FPSO[C].The Twenty-first International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers,2011.

[5] 祝庆斌,王玮,康庄,等.钢悬链立管的敏感性分析与疲劳寿命预估[J].中国海洋平台,2017,32(1):85-90.

[6] 梁宁,黄维平,周阳,等.深吃水半潜式平台钢悬链式立管的强度性能[J].中国海洋平台,2017,32(2):60-68.

[7] FAV Bazán, ECPD Lima, MQD Siqueira, et al. A methodology for structural analysis and optimization of riser connection joints[J]. Applied Ocean Research,2011,33(4):344-365.

[8] 周阳,杨超凡,黄维平.海床土刚度非线性的钢悬链式立管响应分析[J].哈尔滨工程大学学报,2017,38(3):356-362.