单相受热管动态数学模型的改进

徐啸虎 周克毅 韦红旗 黄军林

(东南大学能源热转换及其过程测控教育部重点实验室，南京210096)

单相受热管集总参数建模是电站锅炉实时仿真领域中的重要研究内容之一［1-8］.动态过程中，管壁与工质存在蓄热、储质变化，管壁对工质的放热量一般与稳态计算值并不一致.但建模时，管壁与工质间的放热量基本都采用静态方程计算，这不利于受热管仿真精度的进一步提高.理论分析表明，以出口参数为代表参数的一维集总参数模型，单段上的精度仅同一阶迎风格式相当［8-9］.尽管通过各种分多段方式，如多段串联方法［2］、两段嵌套方法［10］和三段链式方法［11］等，理论上可以提高受热管整体的仿真精度，但就单段控制体而言，上述建模方式并没有本质的区别，单段控制体的精度也没有提高.

为提高集总参数模型在单个控制体上的仿真精度，20 世纪90年代以来，出现了基于动态补偿或修正的建模方法［12-15］.通过对比分析集总参数模型与分布参数模型在系统传递函数上的差异，进而建立用以补偿或修正的数学模型［12-13］，或在集总参数的选择上采用“移动参数”，用以修正模型的输运延迟［14-15］.因补偿或修正环节的特征参数与研究对象有关，此类方法对于特定物理参数及工况的受热管易取得较好的效果.

为使管壁放热量计算能反映管内工质动态过程，提高单段上控制体模型的精度，同时保持多段模型易于显式求解的优点，本文从描述单相受热管动态过程的一维偏微分方程出发，将方程中的时空分离，采用解析和集总参数相结合的方法，建立了一种新的单相受热管动态数学模型(以下简称混合模型).其中，管壁对工质放热量的计算模型不再是静态计算公式，而是同管内工质蓄热和储质过程相关的动态方程.理论分析和仿真结果表明，相同情况下(集总参数均取出口参数)，混合模型比以往采用静态传热公式的集总参数模型更接近分布参数模型;模型在入口温度阶跃响应方面的改进尤为明显，可以更好地反映系统响应的输运延迟特性.

1 建模原理

1.1 描述单相管动态过程的一维微分方程组

一维集总参数的物理模型是在空间上对三维分布参数物理模型进行一维简化后得到的［1-2］，物理模型如图1所示.

描述单相管动态过程的一维微分方程有:

质量守恒方程(连续性方程)

图1 单相受热管物理模型

式中，D 为工质流量;ρ 为工质密度;z 为长度;τ 为时间;F 为管内横截面积.

能量守恒方程

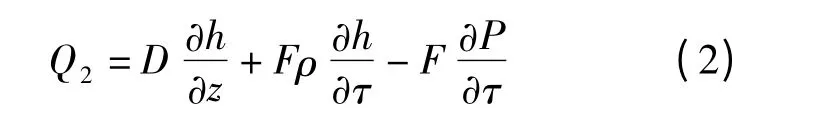
式中，Q2为单位长度上管壁对工质的放热量;h 为工质焓;P 为工作压力.

单位长度上管壁对工质的放热方程

式中，T 为工质温度;Tj为管壁金属温度;α2为管内壁对工质的放热系数，精度和理论分析时近似认为与流量的n 次方成正比，并取n=0.8;K2为比例系数;d2为管内直径;U2为管内壁周长.

动量守恒方程

式中，Pd为单位长度的压损.

热力学状态方程

管壁金属热平衡方程

式中，Q1为单位长度上烟气对管壁的放热量;cj为金属比热;mj为单位长度的金属质量.

式(7)仅在时间维上对管壁温度有热平衡约束，沿长度方向上，管壁温度为集总参数，即0.在采用强制热流量分析受热管动态特性时，方程组不包括烟气侧放热方程.此时，Q1作为预先计算值或边界条件代入计算.以下在精度分析时也将Q1作强制热流量处理.

1.2 工质出口温度和管壁放热量动态方程

由式(6)可得到如下链式表达式:

式中，cp为工质比热.对于同样有:

将式(8)和(9)代入式(2)，得

式中，ω 为工质流速.

考虑到压力-流量通道的动态过程远快于焓-温通道，在进行焓-温通道计算时，通常认为压力-流量通道的动态过程已经结束，即另一方面，对于阻力集中于入口或出口的压力-流量通道模型，认为管内压力是沿空间均匀分布的，即Pd=0.进一步简化式(10)，得

式(11)为时变的非线性偏微分方程，若任一τ 时刻，等式右边项可确定上述方程可转换为常系数的非齐次微分方程.积分并代入τ 时刻的边界条件(Tj－T)z=0=Tj－T1，其解为

式中，T1，T2分别为管内工质入口和出口温度;L 为受热管总长度;A2为管内表面积，A2=U2L.

同样，利用式(11)也可得到沿管长方向任意位置的工质温度，将其代入式(3)并积分，得到管壁对工质的放热量的动态方程:

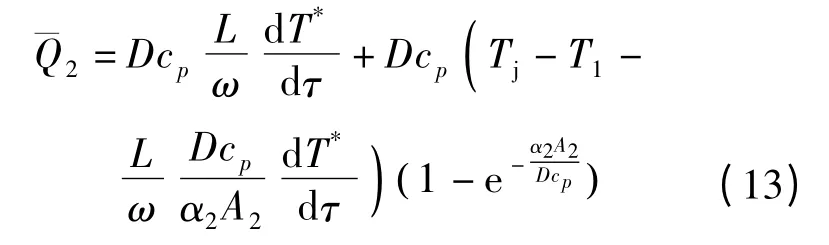
式(7)、(12)和(13)构成了新的单相受热管动态数学模型.模型的推导过程是按照传热微元积分的方法进行的，因此管壁放热量模型反映了管内工质的动态过程，而以往的集总参数模型均不具备这一特点.

为了考察混合模型的最终稳态值，令式(12)和(13)中的时变项得到

式中，下标0 表示稳态时参数.由传热学可知，式(14)、(15)与按对数传热温差计算传热量的稳态方程是等价的，且同参数T*的选择无关.

对于参数T*，从建模的角度分析，也可认为是管内工质的集总参数，可按已有集总参数模型选择.如选择工质出口温度T2，此时方程组待求量为和用矩阵形式可描述为A·y=S，其中

式中，Mj为管壁金属总质量，Mj=mjL;ˉQ1为烟气对受热管的总放热量.

由于混合模型与传统的集总参数模型在形式上存在明显差别，因此有必要对其进行精度分析和仿真实验.在以下分析和计算中，混合模型均采用T2代替T*的形式.

2 模型精度分析

由基本方程(7)、(12)和(13)分别得到工质在入口温度、热流量和流量这3 种扰动下的对象传递函数，并对其在零点(s=0)作泰勒展开，以考察混合模型与分布参数模型［1-2］的逼近程度，以及混合模型相对传统集总参数模型(以下称集总参数模型)的优势.

2.1 传递函数

分别对式(7)、(12)和(13)进行线性化处理，并以时间τ 为自变量进行Laplace 变换，得到入口温度扰动时的传递函数Wη(s)为［16］

式中，Tm为管壁金属蓄热时间常数;ad为动态参数，ad=α20A2/(D0cp);τ0为流动时间，τ0=L/ω0.

热流量扰动时的传递函数Wq(s)为［16］

流量扰动时的传递函数Wd(s)为［16］

2.2 精度分析

理论上常用时域分析法来比较分析热工环节的动态特性.通过对比传递函数在s=0 点的Taylor 展开式，可定性地分析模型间的逼近程度.对于模型在扰动初始时刻和稳态终值方面的响应特性，则可应用Laplace 变换的初值定理和终值定理进行分析.简化的分布参数模型的传递函数有如下形式［2］:

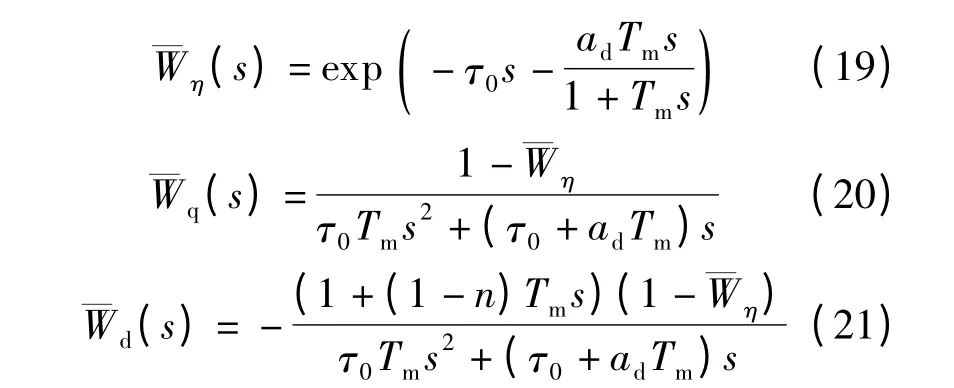
在相同条件下，集总参数模型的传递函数为［1］

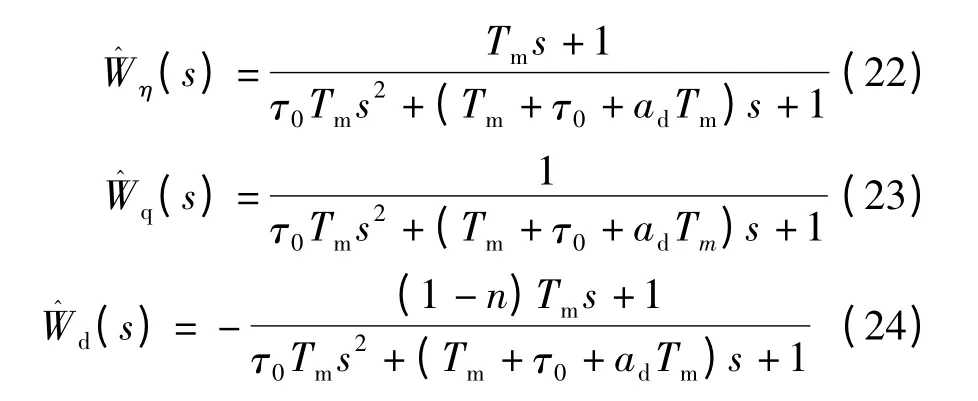
根据Laplace 初值定理和终值定理，易得到在s→∞和s→0 时混合模型的3 个传递函数均与分布参数模型对应的传递函数的计算结果一致.这表明，混合模型在动态响应的初值和终值方面均无误差.将式(16)～(24)在s=0 处作Taylor 展开，省略高阶项后得到3 种模型入口温度扰动传递函数的Taylor 展开式:

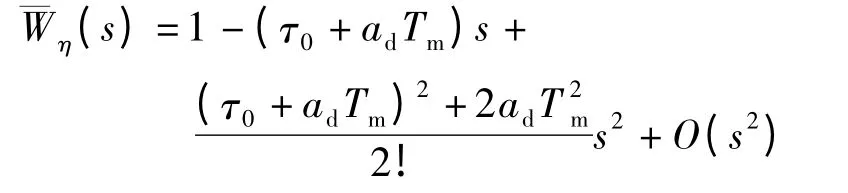
得到的3 种模型热流量扰动传递函数的Taylor 展开式如下:

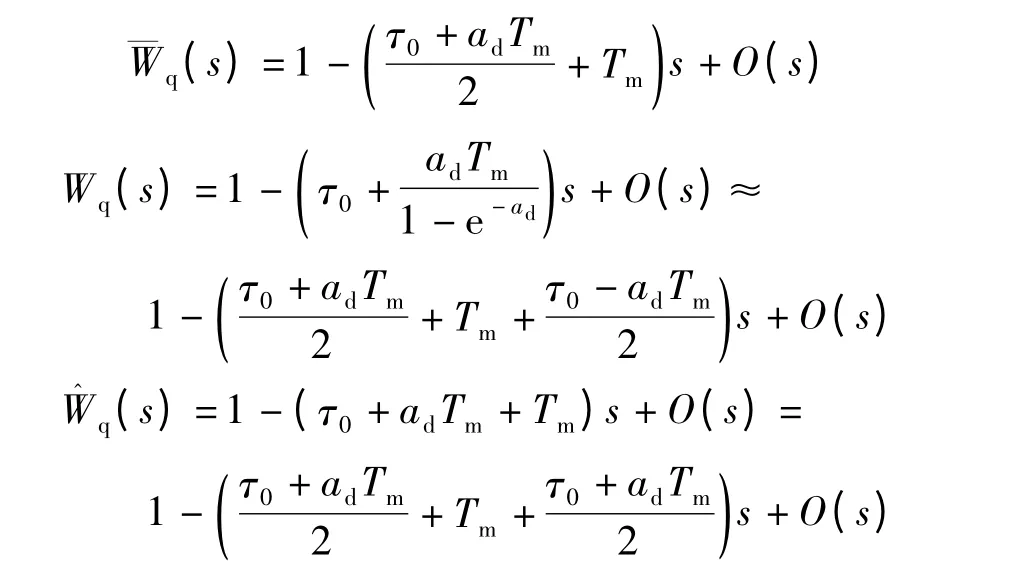
得到的3 种模型流量扰动传递函数的Taylor 展开式如下:

分别将混合模型、集总参数模型与分布参数模型所对应的传递函数相减，对于入口温度扰动的传递函数，二阶精度上的比较结果为

对于热流量扰动的传递函数，一阶精度上的比较结果为

对于流量扰动的传递函数(n=0.8)，一阶精度上的比较结果为

以上分析表明，同样选择工质出口参数为集总参数的情况下，混合模型比集总参数模型更加接近于分布参数模型.

2.3 仿真结果比较

2.2 节理论精度分析是在不分段的情况下进行的，分析内容也仅限于在s=0 处作Taylor 展开.为进一步说明3 种模型在动态过程的差异，有必要进行仿真计算比较.仿真计算的对象为某超超临界压力锅炉的过热器，管内工质压力为26.7 MPa，特征参数τ0=4.0 s，Tm=21.8 s.三种扰动的仿真结果对比如图2所示.

图2 入口参数阶跃扰动后出口温度响应(物性不变)

从仿真结果可看出，集总参数模型和混合模型的响应趋势与分布参数基本一致，但混合模型的响应过程均介于集总参数模型和分布参数模型之间.即在相同分段数情况下，混合模型的计算结果都更接近于分布参数模型，尤其是在入口温度扰动时，3段混合模型的精度明显高于5 段集总参数模型.

3 考虑物性变化的混合数学模型

为考虑工质储质和蓄热过程对管壁放热量的影响，还需补充连续性方程.结合传统的多段集总参数建模思想，将受热管沿管长均分为n 段，其中第i 段的物理模型如图3所示.

图3 考虑物性变化的单个控制体物理模型

3.1 考虑物性变化的连续性方程

密度对时间的偏导数存在如下链式关系:

将式(25)代入式(1)，推导得到第i 段内工质的连续性方程:

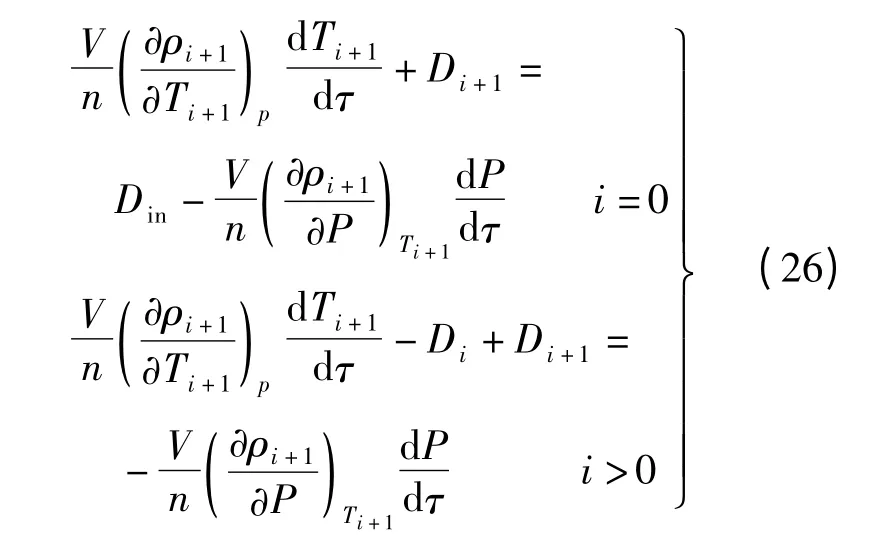
式中，V 为管内总容积，V=FL;Din为受热管入口流量.

式(26)与式(7)、(12)、(13)一起构成了考虑物性变化的混合模型.各段模型中的待求量分别为工质出口温度、管壁金属壁温、流量和管壁对工质的放热量，且均为显式形式.当受热管均分为n 段时，待求参数向量y 共有4n 个元素，表示为

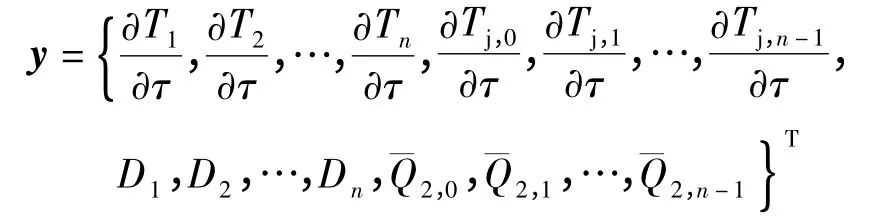
3.2 考虑物性变化时的仿真结果对比

分别建立单相受热管多段混合模型与多段集总参数模型.仿真对象与2.3 节一致，时间步长均取0.1 s.计算结果如图4所示.其中，用来比较的分布参数模型是通过流体力学计算软件FLUENT建立的.采用FLUENT 数值模型可充分利用其中已有的大量经验证的、较成熟的数学模型及其算法，确保混合模型、集总参数模型对比验证的合理性.

图4 入口参数阶跃扰动后出口温度响应(物性变化)

计算结果显示，在相同条件下，混合模型比集总参数模型更接近分布参数模型的计算结果.尤其是在入口温度阶跃响应方面，3 段混合模型的初始响应便可较好地表现出管内工质特有的输运延迟现象，且同分布参数模型基本一致，而集总参数模型则与分布参数模型相差较大.

此外，混合模型的稳态方程与按对数传热温差求解传热量的计算公式是等价的，但两者在形式上并不一致.混合模型不会出现对数传热温差计算病态问题，其动态方程对大扰动也有很好的适应性，可用于锅炉全工况的实时仿真计算［16］.

4 结论

1)混合模型是从描述受热管传热和流动的一维偏微分方程出发，按照传热微元积分的方式推导得到的，符合单相受热管动态过程机理.

2)由于管壁放热量的动态方程反映了管内工质蓄热和储质过程对其计算值的影响，且其稳态值与按对数传热温差计算传热量的方程是等价的，使得模型在单个控制体上的仿真精度优于常用的多段集总参数模型;精度分析表明，即使不考虑物性变化，混合模型的仿真精度也高于传统的集总参数模型.

3)仿真结果表明，相比入口流量和热流量的阶跃响应，混合模型对入口温度阶跃响应的改进尤为突出，能更好地反映系统响应的输运延迟特性.

4)管内工质集总参数的选择具有独立性，这给模型的具体应用带来较高的自由度和通用性.既可以按多段串联的方式建模，也可按多段嵌套或链式方式建模;对于特定研究对象，也可以按照移动参数方式建立相关数学模型.

References)

［1］ 吕崇德，任挺进，姜学智，等.大型火电机组系统仿真与建模［M］.北京:清华大学出版社，2002.

［2］ 章臣樾.锅炉动态特性及其数学模型［M］.北京:水利电力出版社，1987.

［3］ Liu Changliang，Wang Hong，Ding Jinliang，et al.An overview of modelling and simulation of thermal power plant［C］//2011 International Conference on Advanced Mechatronic Systems.Zhengzhou，China，2011:86-91.

［4］ Oko E，Wang M H.Dynamic modelling，validation and analysis of coal-fired subcritical power plant［J］.Fuel，2014，135(6):292-300.

［5］ Hou G L，Huang F R，Sun T Y，et al.Mathematical model for ultra-supercritical unit by physical principles［C］//IEEE 9th Conference on Industrial Electronics and Applications.Beijing，China，2014:781-786.

［6］ Chandrasekharan S，Panda R C，Swaminathan B N.Modeling，identification，and control of coal-fired thermal power plants［J］.Reviews in Chemical Engineering，2014，30(2):1-17.(in Chinese)

［7］ 梁庆姣，刘吉臻，薛彦广，等.超超临界机组的非线性模型及动态特性研究［J］.动力工程学报，2012，32(2):118-123.Liang Qingjiao，Liu Jizhen，Xue Yanguang，et al.A non-linear model for ultra-supercritical power unit and the dynamic characteristic study［J］.Journal of Chinese Society of Power Engineering，2012，32(2):118-123.(in Chinese)

［8］ 王泽宁，周强泰.单相受热管通用数学模型［J］.东南大学学报:自然科学版，1994，24(S1):83-89.Wang Zening，Zhou Qiangtai.A universal mathematical model for single-phase heated tubes［J］.Journal of Southeast University:Natural Science Edition，1994，24(S1):83-89.(in Chinese)

［9］ 王泽宁，周强泰，孔红军.单相受热管集中参数简化模型的讨论［J］.中国电机工程学报，1993，13(4):44-51.Wang Zening，Zhou Qiangtai，Kong Hongjun.Investigation on the simplified lumped-parameter model of single-phase heated tubes［J］.Proceedings of the CSEE，1993，13(4):44-51.(in Chinese)

［10］ 范永胜，徐治皋，陈来九.锅炉单相区段的嵌套建模方法［J］.动力工程，1995，15(5):7-12.Fang Yongsheng，Xu Zhigao，Chen Laijiu.A insertion modelling method applied to uni-phase boiler sections［J］.Power Engineering，1995，15(5):7-12.(in Chinese)

［11］ 任挺进，谢茂清，李志刚，等.锅炉单相受热面链式建模新方法［J］.中国电机工程学报，2003，23(3):175-178.Ren Tingjin，Xie Maoqing，Li Zhigang，et al.A new method of chain structure modeling on boiler’s singlephase heat-exchanger［J］.Proceedings of the CSEE，2003，23(3):175-178.(in Chinese)

［12］ 范永胜，眭喆，姜学智，等.一种高精度的锅炉单相区段集总参数动态修正模型［J］.中国电机工程学报，2000，20(1):50-54.Fan Yongsheng，Shui Zhe，Jiang Xuezhi，et al.A highprecision modified lumped-parameter dynamic model applied to uniphase boiler section［J］.Proceedings of the CSEE，2000，20(1):50-54.(in Chinese)

［13］ 闫水保，李晶晶，张晓东，等.电站过热汽温建模方法的改进［J］.郑州大学学报:工学版，2012，33(1):55-58.Yan Shuibao，Li Jingjing，Zhang Xiaodong，et al.Improved modelling method of superheated steam in power plant［J］.Journal of Zhengzhou University:Engineering Science，2012，33(1):55-58.(in Chinese)

［14］ 刘笑驰，蔡瑞忠，吕崇德.单相受热管的移动参数模型［J］.清华大学学报:自然科学版，2003，43(6):772-774，790.Liu Xiaochi，Cai Ruizhong，Lü Chongde.Moving parameter model for single phase flow in heated pipes［J］.Journal of Tsinghua University:Science ＆Technology，2003，43(6):772-774，790.(in Chinese)

［15］ 陈钢，任挺进.单相受热管移动参数模型的修正［J］.清华大学学报:自然科学版，2007，47(5):695-698.Chen Gang，Ren Tingjin.Moving parameter model modification for single phase flow in heated pipes［J］.Journal of Tsinghua University:Science ＆Technology，2007，47(5):695-698.(in Chinese)

［16］ 徐啸虎.超临界压力锅炉汽水系统动态特性及其数学模型［D］.南京:东南大学能源与环境学院，2013.