双馈风力发电机无速度传感器控制研究

2015-03-12李金杰张继勇柏龙青

微特电机 2015年8期

李金杰，张继勇，柏龙青，郭鑫

(1.南京中人能源科技有限公司，南京211102;2.扬州大学，扬州225127;3.南通大学，南通226019;4.南京广播电视集团，南京210001)

0 引言

目前，双馈风力发电系统均采用有速度传感器的矢量控制技术［1-3］。速度传感器的安装不仅给系统的维护带来了困难，还增加了风力发电系统的成本，降低了系统的可靠性，所以无速度传感器控制技术的研究具有重要意义，成为近年来的研究热点［4-5］。

双馈风力发电机无速度传感器控制的关键是转子位置和转速的精确辨识，本文结合双馈风力发电机定子电压定向矢量控制的基本原理，通过容易检测到的定子电压、电流和转子电流以及双馈电机数学模型的分析，提出一种新的基于MRAS 双馈风力发电机无速度传感器矢量控制方案，并在理论分析、Simulink 仿真的基础上和双馈风力发电机组实验平台上进行了亚同步和超同步以及在低转速下的不同工作方式的实验，实现了对转子速度和转子位置的精确辨识，实验结果表明了本文提出的双馈风力发电机组无速度传感器矢量控制方案的可行性和正确性。

1 数学模型［6］

采用电动机惯例，假定定、转子三相绕组对称且不考虑零轴分量，则DFIG 在d -q 两相同步旋转坐标系下的数学模型:

磁链方程:

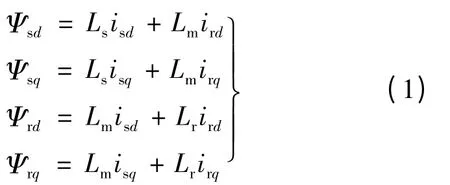
电压方程:

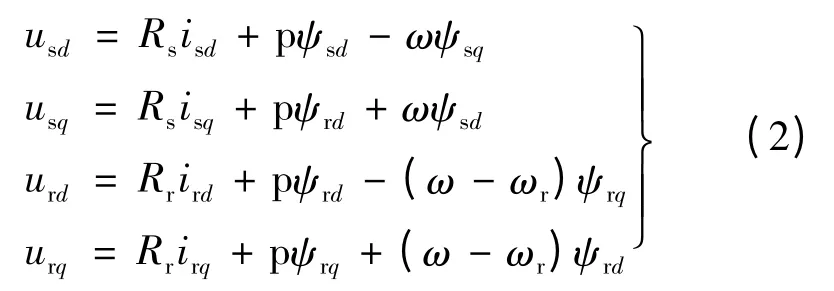
电磁转矩方程:

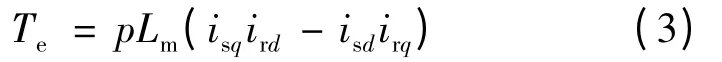
式中:Ψsd，Ψsq，Ψrd，Ψrq，usd，usq，urd，urq，isd，isq，ird，irq分别为定、转子磁链和电压以及电流在d，q 轴的分量;Lm，Ls，Lr分别为定子和转子同轴等效互感、定子等效自感、转子等效自感;Rs，Rr分别为定、转子电阻;p 为微分算子;Te为电磁转矩;ω，ωr分别为同步电角速度、转子电角速度。

传统的定子磁链定向矢量控制中要对定子磁链进行观测，在一定程度上增加了系统的控制性，并且定子电压定向矢量控制中，当机组并网时，定子电压就是电网电压且电网电压不受电机参数影响，可以直接测量，更具有准确性［7-8］。

当同步旋转坐标系的d 轴定向于定子电压矢量Us上时，有:

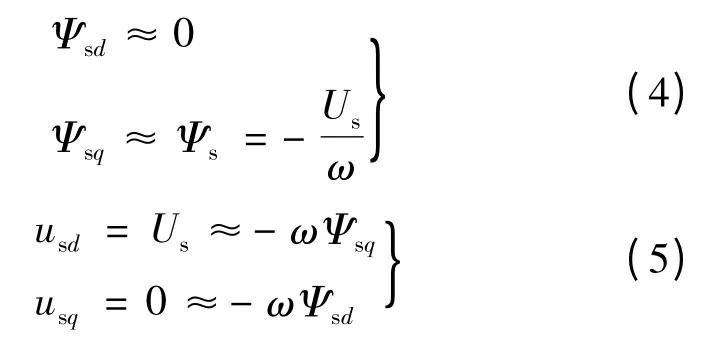
式中:Us为电压矢量的幅值。

在定子电压定向条件下，DFIG 定子输出有功、无功功率与转子d，q 轴电流的关系:

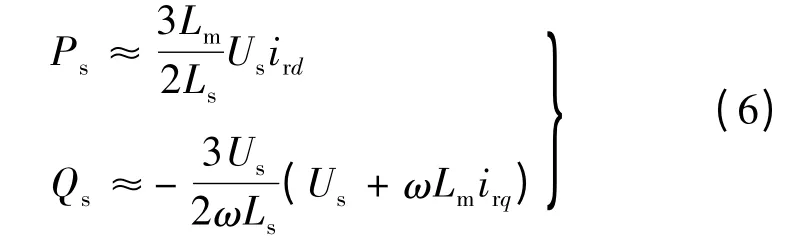
由上述可知，控制转子电流d、q 轴分量就可以控制有功功率和无功功率。

2 转速辨识

在定子电压矢量控制同步转速旋转坐标系下，由式(1)和式(5)得转子磁链模型:

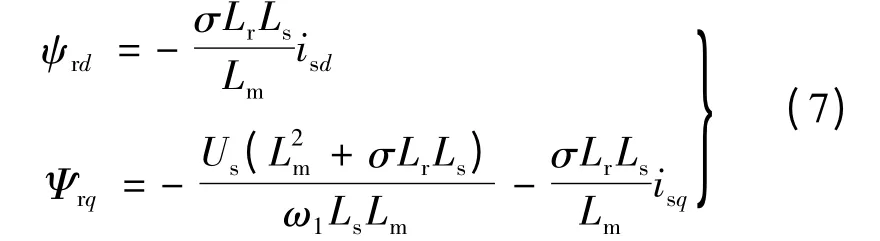
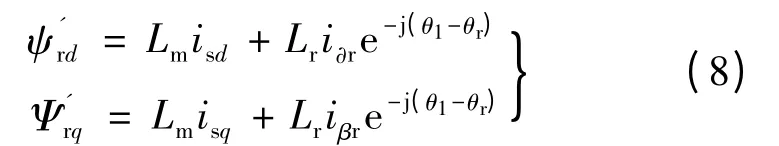
式中:iα，iβ是静止坐标系下的转子电流，可以直接测量得到。

实际测得的磁链模型不含有θr项，而估测模型含有θr项，因此，选取Ψr作为参考模型，Ψ'r 作为自适应模型，其控制系统如图1 所示。

在MRAS 辨识系统中，系统的全局稳定性必须要考虑，由于电气实际常数比电机时间常数小得多，式(8)中的θr可看作常数，则自适应模型可视作为一个线性状态方程，因此，本设计系统稳定［9-10］。而且，由于转子磁链角出现偏差时，同步旋转坐标系下的转子磁链的实际值与估测值也会存在一定的误差，其基本原理如图2 所示。本文的关键就是消除这两个转子磁链角度差。

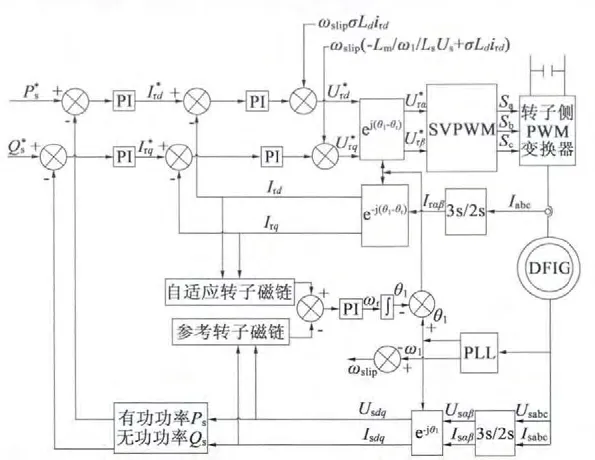
图1 基于定子电压定向矢量控制框图

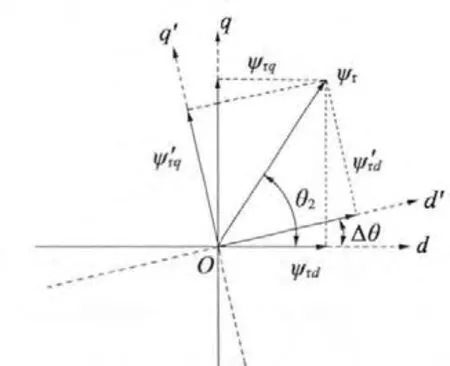
图2 转子磁链角度偏差与定子电压的关系

假设同步坐标系下转子磁链的实际值:

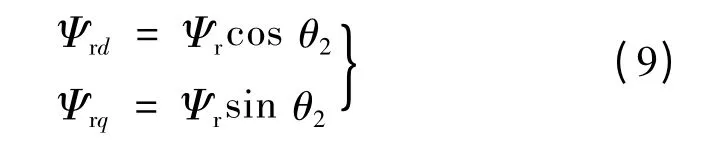
由于转子磁链角度的偏差，同步坐标系下转子磁链的测量值:

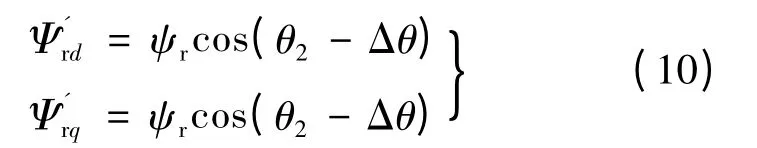
式中:Δθ 为转子磁链位置角误差。

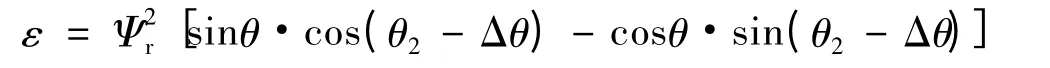
经三角函数和化积差得:

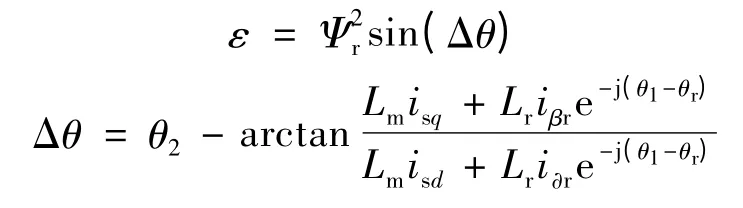
通过PI 自适应控制器将不断的调节θr，使转子磁链位置角误差Δθ 越来越小，且Ψr和Ψ'r 基本保持一致，相对误差ε 趋近于零。

3 仿真实验

为了验证上述原理和新的控制方案的有效性，在MATLAB/Simulink 平台上进行了DFIG 风力发电系统的仿真［11-12］。系统仿真参数:双馈电机额定功率为7.5 kW，额定线电压380 V，额定电流20 A，额定转速750 r/min，转动惯量Jm=0.2 kg·m2，定子电阻Rs=1.25 Ω，转子电阻Rr=0.035 49 Ω，转子电感Llr=0.009 745 66 H，定子电感Lls=0.092 733 21 H，互感Lm=0.067 751 33 H。网侧进线电感L=0.001 H，电阻R=0.1 Ω。直流母线电压Udc=650 V，母线电容C =4 000 μF，网侧额定线电压380 V，频率50 Hz。

图3 所示给出了双馈电机在无速度传感器矢量控制下的电机转速从亚同步变换到超同步情况下的仿真图形。由图3 可知，在此方案下，双馈电机不但在动态时能够较好较快地跟踪实际转速，而且在稳态情况下电机转速误差趋近于零，因此，本文提出的无速度传感器控制方案具有可行性。图4 是实际转子角度和估测转子角度实验波形。

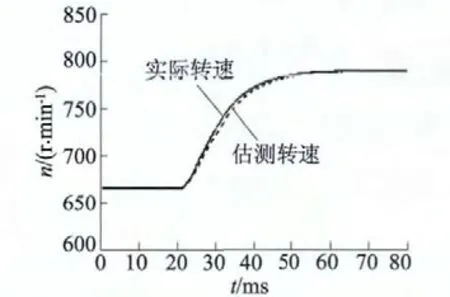
图3 电机实际转速与估测转速仿真波形

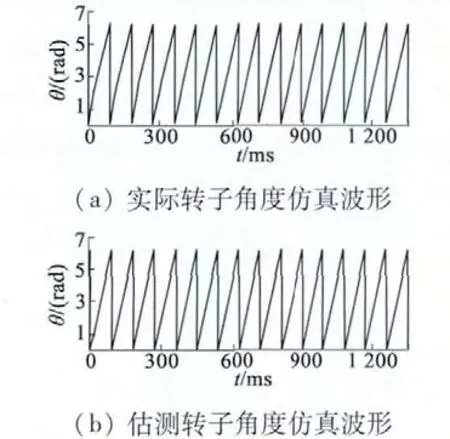
图4 实际转子角度与估测转子角度仿真波形

4 系统实验

为了更进一步验证此方案的理论和方法，利用实验室的双馈风力发电实验平台，进行了实验与研究。该实验平台采用双PWM 变换器，以及以TMS320F28335 为核心的DSP 控制芯片，配备EPIC12Q240I8 型FPGA 作为辅助控制器。双馈风力发电机的系统实验参数与仿真系统参数相同。

由图5、图6、图7 可知，当原动机使转子速度处于亚同步向超同步变化以及电机低速运行时，电机的实际转速由光电编码器测得，转速变化很快［13］。而估测转速的跟踪具有一定时间的延时，但是也能较快、较准地跟随实际转速。当转速处于稳定时，估测转速趋近于实际转速，系统动态性能良好，静差小，所以此方案可以准确地实现双馈风力发电机无速度传感器的矢量控制。

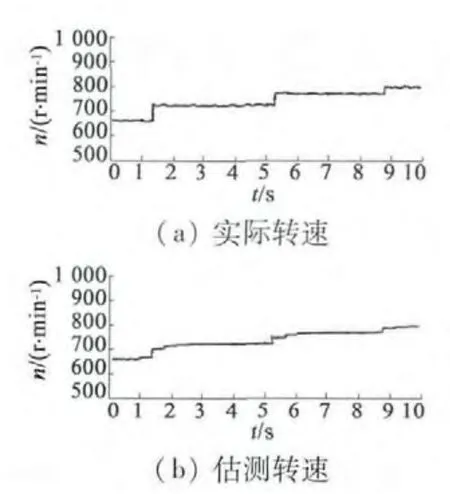
图5 电机实际转速与估测转速实验波形

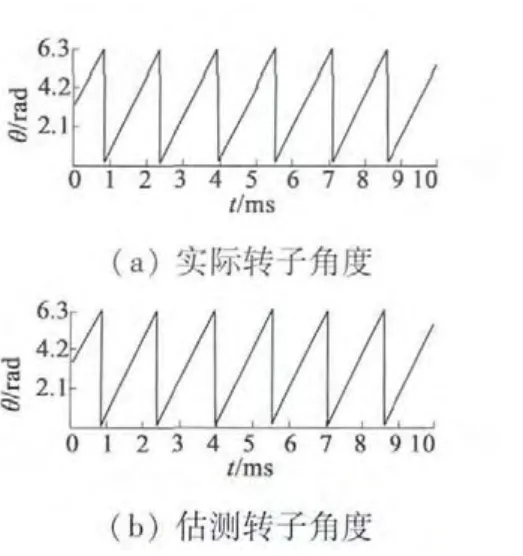
图6 实际转子角度与估测转子角度实验波形

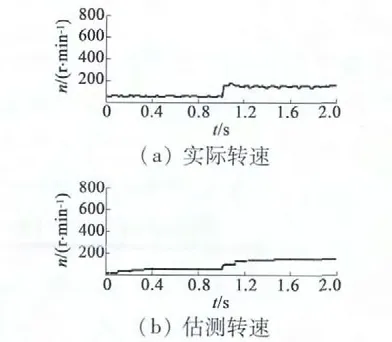
图7 实际转子与估测转子低速时实验波形

5 结语

常规的模型参考方法中引入了积分环节，因而存在了积分漂移的问题，虽然可以利用高通滤波器抑制积分漂移，但是其低速性能受到很大的影响［14-15］。针对这一问题，本文结合模型参考自适应法(MRAS)和定子电压定向矢量控制的特点，以及通过对双馈风力发电机的数学模型推导，提出了一种新的基于MRAS 双馈风力发电机无速度传感器矢量控制方案。此方案经过了系统的理论分析，Simulink 仿真和系统实验，结果证明了此方案的正确性和有效性，在不同的工作方式下系统响应快速且平稳，不仅具有超调量小、响应速度快，且在低速和高速时也能够满足双馈风力发电无速度矢量控制要求，具有广阔的发展前景。

［1］ MULLER S，DEICKE M，De Doncker，et al.Adjustable speed generators for wind turbines based on doubly-fed induction machines and quadrant IGBT converters linked to the rotor［J］.IEEE Transactions on Industry Applications，2000，30(3):231 -241.

［2］ PERESADA S，TILLI A，TONIELLI A. Power control of a doubly fed induction machine via output feedback［J］. Control Engineering Practice，2004，12(1):41 -57.

［3］智泽英，韩如成.无速度传感器异步电动机控制中的速度估算方法及比较［J］.太原重型机械学院学报，2001，22(2):160 -165.

［4］ SH N M H，HYUN D S，CHO S B，et al.An improved stator fluxe stimationson paver electronics［J］. Power Engineering Journal，2000，15(2):312 -318.

［5］刘丛伟，李崇坚，苏鹏声，等.双馈电机无速度传感器控制调速系统的研究［J］.清华大学学报，1999，39(5):54 -57.

［6］贺益康，胡家兵，徐列. 并网双馈异步风力发电机运行控制［M］.北京:中国电力出版社，2011.

［7］暴国辉，梅柏杉，邓德卫，等.定子磁场定向无速度传感器异步电机控制系统研究［J］.电气开关，2014，52(3):27 -32.

［8］丰胜成.定子磁链定向双馈电机转子初始角直接求解法［J］.问题探讨，2009，18(9):49 -51.

［9］杨胤铎，李汉强.基于磁通观测器无速度传感器转差频率型矢量控制系统［J］.武汉理工大学报，2002，5(10):646 -649.

［10］肖兵，薛琦，余师棠.基于DSP 的M/T 测速法改进［J］. 重庆工学院学报，2009，23(10):65 -76.

［11］苏小林，赵巧娥著.MATLAB 及其在电气工程中的应用［M］.北京:机械工业出版社，2014.

［12］张惠萍，施火泉. MATLAB 环境下的异步电动机的数学模型及仿真研究［J］.淮阴工学院学报，2003，12(3):41 -44.

［13］任志斌.电动机的DSP 控制技术与实践［M］.北京:中国电力出版社，2013.

［14］吴雪芬.一种能消除积分漂移的电压型磁链观测器［J］.机电工程，2007，24(8):14 -16.