优化灰色预测补偿永磁同步电动机转速控制

张 蓉，骆光照，张 莎，涂文聪

(西北工业大学，西安710129)

0 引 言

当前，诸如太阳能无人机、多电飞机等新型航空航天器电驱动系统对控制性能要求很高，而永磁同步电动机(以下简称PMSM)作为一种驱动装置，具有功率密度高、体积小、运行可靠、维护方便等特点，受到广泛关注［1-2］。

然而，在对PMSM 转速控制时，经常受到噪声、运行环境、温度、参数变化以及负载干扰等不确定因素的影响［3-4］，很难建立确定的PMSM 转速控制模型。

为了改善这些不确定性，提高转速的跟踪性能和鲁棒性，很多学者也进行了相关的研究。文献［5］采用鲁棒模型参考自适应控制方法，运用李雅谱诺夫稳定性理论，针对不确定参数带来的影响，设计了转速环和电流环的PI 控制参数，达到改善PMSM 转速跟随性能的目的;文献［6］采用带有前馈控制的电压参考模型鲁棒自适应控制，对干扰带来的不确定部分，设计了一种自适应干扰观测器，探讨了PMSM 在不同工作条件下对转速的控制性能。这些方法主要是对当前获得的值进行调节，一定程度上会影响系统的实时性。文献［7］在传统PID 控制器的基础上，采用灰色理论对转子转速不确定部分进行预测和补偿，设计了一种基于灰色预测补偿的转子转速PID 控制器，对未来的不确定影响进行了超前预测和补偿，提高了系统的实时性，并克服了不确定部分带来的影响。但是，实际模型总会与理想模型存在差异，没有一定的参考模型进行参考校正，会使得整个系统的输出标准没有约束，或者使达到给定值的时间延长。

PMSM 运行过程中的不确定干扰项多呈现随机性、复杂性、易受环境影响等特点，使得PMSM 转速偏差难以预知，即为灰色的。根据这一点，本文在经典矢量控制的基础上，对理想条件和实际控制中存在的噪声及扰动情况下获得的转速值进行比较，根据这一比较而得到的误差不确定项，采用灰色系统理论建立灰色预测模型，对因干扰项的存在而产生的转速偏差进行超前预测，进而对实际控制过程予以实时补偿，提高PMSM 的转速跟踪性能和鲁棒性。然而，灰色预测方法对于初值的选取比较敏感，传统方法将初值取为原始序列的第一个值，但是随着预测值的实时更新，这样的初值并不能反映实际预测情况，而且随着预测长度的增加，与初值距离也越来越远，规律性被弱化。针对这一点，首先提出了一种初值动态待定的方法，将灰色预测算法进行优化，然后再运用于PMSM 转速控制中。

1 PMSM 转速模型

为了研究问题方便，采用d -q 旋转坐标系，同时考虑不确定部分，则PMSM 的转速数学模型如下:

转速方程:

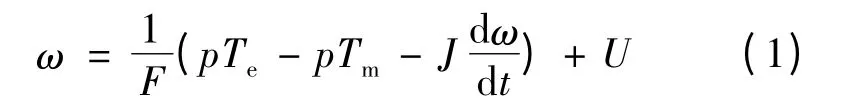
电磁转矩方程:

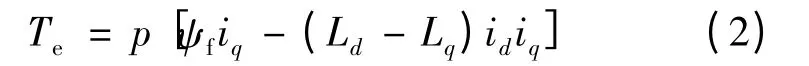
式中:id，iq分别为d-q 坐标下的电流;ψf为转子永磁体磁链;Ld，Lq为d -q 坐标系下的定子电感值;p为极对数;F 为粘滞系数;J 为转动惯量;ω 为转子电角速度;Tm为负载转矩;Te为电磁转矩;U 为噪声及扰动条件下转速的不确定部分。

2 优化灰色补偿控制策略

2.1 传统灰色算法

灰色预测是通过挖掘已获得数据之间的关系，预测其未来的变化趋势［8］。其基本建立过程如下:

假设获取了一组原始序列:

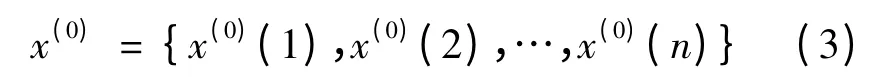
其中，n 表示序列的长度。将此序列按式(4)进行一次累加，即:

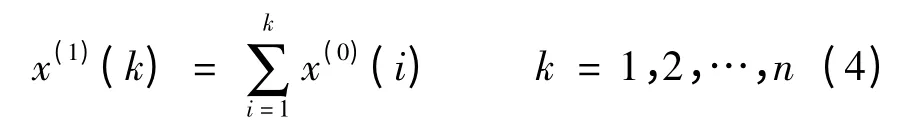
得到一次累加序列:

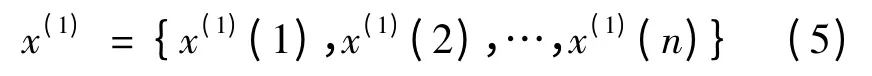
还原为原始序列，即:

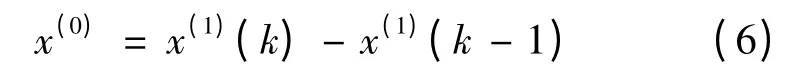
白化方程组:

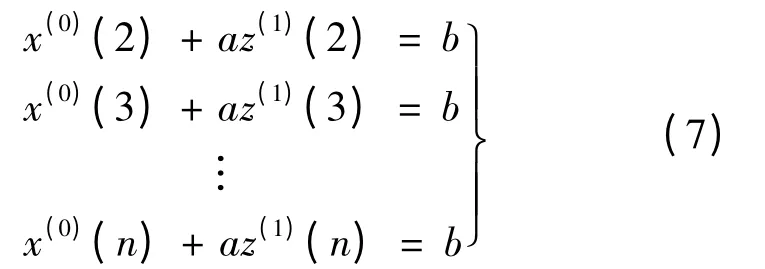
式中:a，b 为待估参数。

通过最小二乘求解公式可得待估参数a，b 满足:

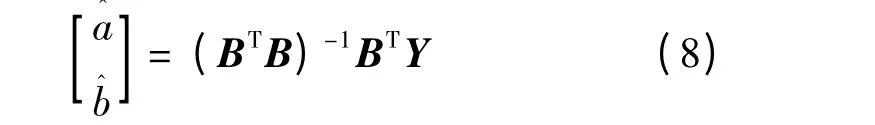
其中:

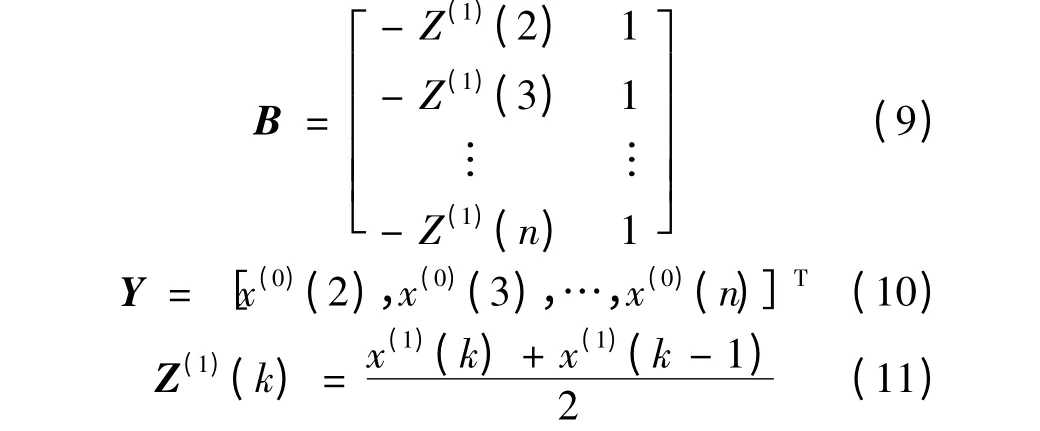
解微分方程得到:

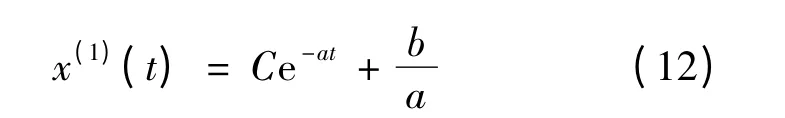
为了求解常数项C，把x(0)(1)作为求解微分方程的初值，得到的灰色预测模型:

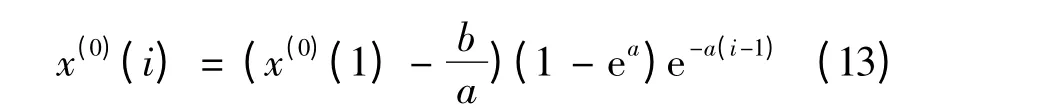
2.2 优化灰色预测

可以看出，传统灰色算法把初值选为原始序列的第一个值，然而随着预测值的更新，这样的初值选取方法并不能反映最新的预测结果，而且此初值与预测的距离越来越远，数据间的规律性逐渐被弱化，预测精度将受到影响。于是可以考虑初值动态待定的方法，得到一种实时跟随预测值的优化算法。具体实现过程如下:对于已有的n 个数据，根据式(12)，初值先待定，则常数项:

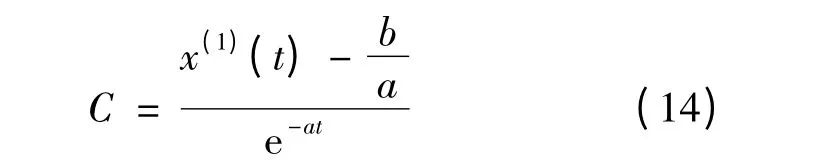
令式(14)中t=k，再将式(14)代入式(12)得到:

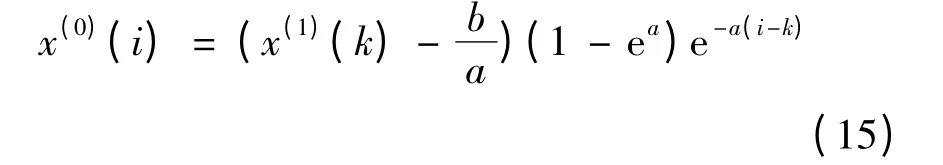
此时取k=i，则:

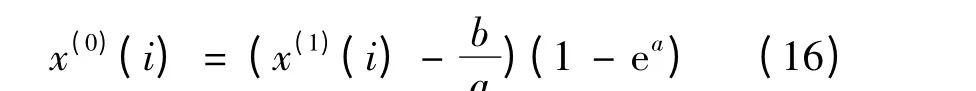
式中:i=1，2，…，n。

在此基础上，得到对原始序列的第n 个数的预测值，其规律性将更强，然后把预测的此序列按式(4)进行累加得到:

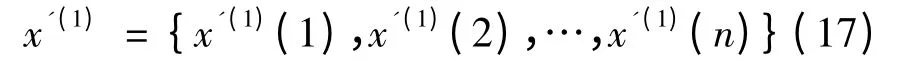
取最近的值x'(1)(n)为初值，同时a，b 值也相应改变，得到:

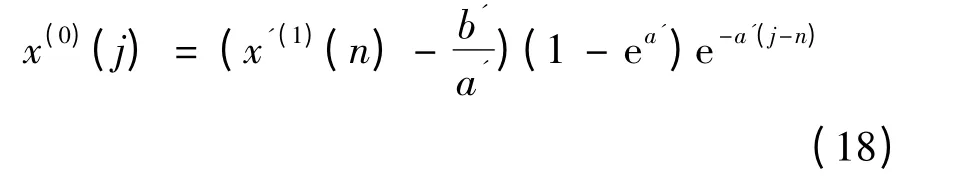
式中:i=1，2，…，n;j=n+1，n+2，…。

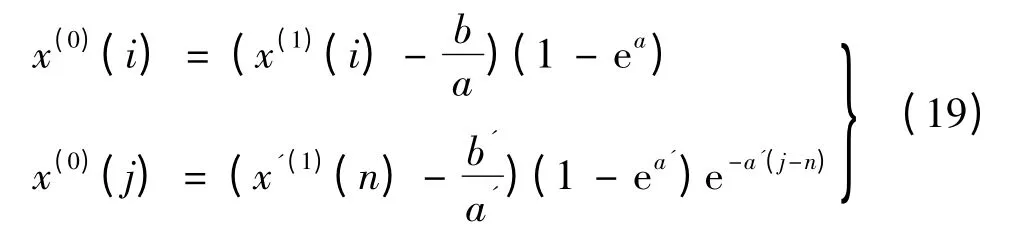
3 PMSM 优化灰色补偿控制

PMSM 矢量控制模拟直流电机性能，因具有转矩响应特性快、精度高等控制性能而广泛用于电机控制领域［9-10］。它通过模拟直流电机控制简单、高效的控制规律，对磁场定向，将电流矢量分解为相互垂直和独立的两个电流分量，然后分别调节，达到PMSM 高性能控制的目的。然而在有干扰存在的情况下，会对矢量控制的精度和快速性产生一定的影响，因此首先对理想情况及干扰条件下得到的转速误差进行采样，得到的转速误差采样序列为Δω(0)={Δω(0)(1)，Δω(0)(2)，…，Δω(0)(n)}，再根据推导出的式(19)，对因干扰而产生的速度偏差进行灰色超前预测，可得预测公式:

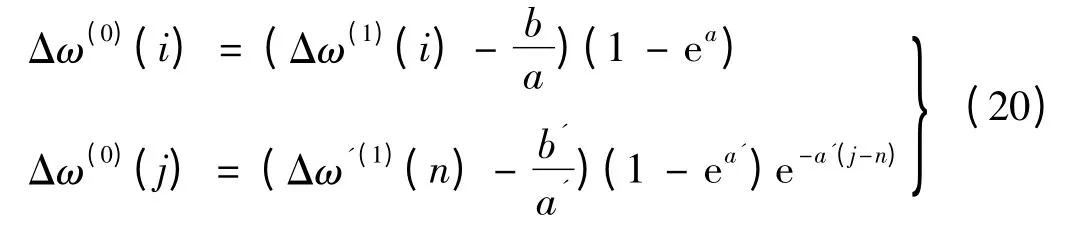
式中:i=1，2，…，n;j=n+1，n+2，…。

根据式(20)得到的转速误差预测值，用理想条件下的输出模型作为参考，将此预测值予以实时补偿，提高系统的控制精度和鲁棒性。整个控制系统结构图如图1 所示。

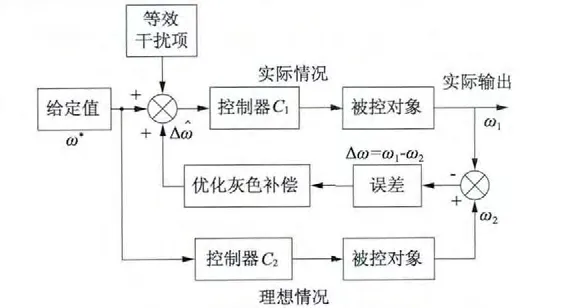
图1 优化灰色补偿控制算法框图

4 仿真分析

为验证控制算法对负载干扰及电机参数变化的有效性，根据图1 的控制框图，在MATLAB/Simulink 中搭建具体的仿真模型，如图2 所示。采用双闭环id=0 矢量控制策略，选取270 V直流供电的三相电压型逆变器，其中灰色补偿部分采用本文提出的优化算法。PMSM 的参数:Rs=0.054 5 Ω，p =2，L=0.226 589 mH，J =0.000 709 7 kg·m2，ψf=0.061 268 9 V·s，TL=25 N·m。

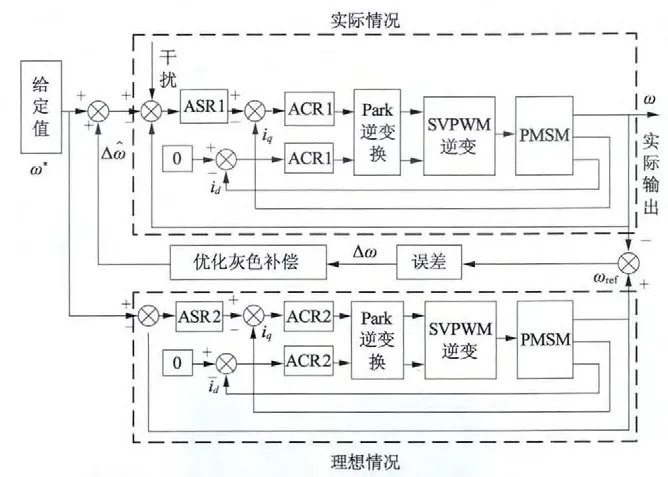
图2 PMSM 优化灰色补偿控制系统结构框图

为了验证本文所提出的PMSM 优化灰色补偿转速控制策略的有效性，与经典矢量控制算法进行了对比，通过以下两种情况进行分析:

(1)电机在运行过程中，经常会受到负载干扰的影响，为此在t=0.3 s 时突加额定负载扰动，分析控制系统的抗负载干扰特性，得到的仿真波形如图3 所示。

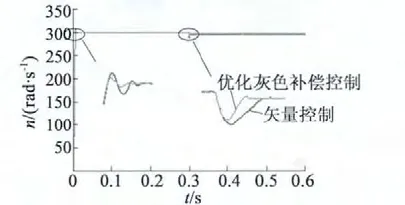
图3 突加负载时转速跟踪对比曲线

(2)电机起动过程中有时需带载起动，此时电机的转动惯量会受到影响，从而影响电机的转速跟踪性能和快速性。为此在电机起动时加额定负载并改变电机转动惯量为10JN，分析控制系统对电机参数变化的抗干扰性，得到的仿真波形如图4 所示。

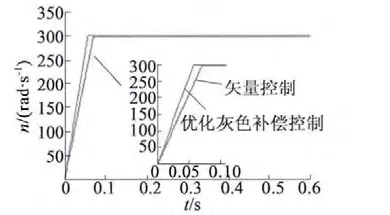
图4 额定负载+10JN 起动时转速跟踪对比曲线

从图3 和图4 中可以看出，与经典矢量控制相比，本文所提控制策略在空载起动过程中的转速经过小幅度振荡即可跟随给定转速;突加负载干扰时，转速经过较小波动后能迅速恢复，恢复时间短，抗干扰性能良好，而且脉动幅度也比经典矢量控制策略下的小;电机转动惯量变化时，转速上升时间缩短，并能很快跟随给定转速。验证了本文所提控制算法能改善PMSM 的转速动态响应性能。

5 dSPACE 半物理实验验证

为了进一步验证该算法在实际的PMSM 控制中的有效性，搭建了控制系统实验验证平台，如图5所示。它主要包括控制与驱动电路、上位机、dSPACE 半物理仿真系统、表贴式PMSM 等。其中控制板采用TMS320F2812，并配合EPM1270 做逻辑处理与保护功能，实际电机参数参见仿真部分。为了验证本文所提算法的有效性，得到的实际电机运行过程中的转速波形如图6 所示。同时也给出了与理想条件下传统矢量控制相比的转速误差曲线，如图7 所示。

图5 实验平台

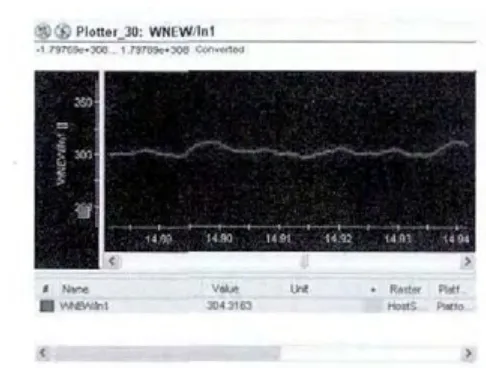
图6 优化灰色补偿PMSM转速曲线

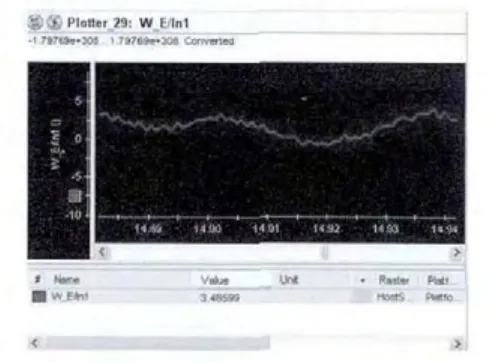
图7 与理想条件下矢量控制相比的转速误差曲线

通过图6 得到的dSPACE 半物理实验结果可以看出，本文所提控制策略能够很好地跟踪给定转速，跟踪性能良好。同时，从图7 可以看出，由于电机在实际运行过程中存在各种干扰影响，而采用本文所提优化灰色预测补偿的控制策略得到的输出转速，与理想条件下矢量控制的输出转速相比，误差在4 rad/s的范围内，转速波动幅度小，相当于实际运行的电机采用本文所提算法控制后，控制性能接近于理想条件下的矢量控制，从而进一步验证了本文所提的基于优化灰色补偿的PMSM 控制策略的有效性。

6 结 语

针对PMSM 运行过程中存在的不可预测干扰，影响转速跟随性能及抗干扰性能的问题，本文提出了一种基于经典矢量控制的优化灰色补偿PMSM转速控制方法，通过仿真和dSPACE 半物理实验，验证了所提控制策略的有效性，为PMSM 高性能控制提供了一定的参考。

［1］ KUNG Y - S，TSAI M - H. FPGA - based speed control IC for PMSM drive with adaptive fuzzy control［J］.IEEE Transactions on Power Electronics，2007，22(6):2476 -2486.

［2］ 王亮，朱臻赜，马跃江，等.系统参数变化对同步电机性能影响的研究［J］.微特电机，2014，42(9):33 -35.

［3］ 刘栋良，贺益康，严伟灿.基于灰色预测的永磁同步电动机速度控制［J］.仪器仪表学报，2007，28(1):145 -149.

［4］ 方一鸣，任少冲，王志杰，等.永磁同步电动机转速自适应模糊Backstepping 控制［J］. 电机与控制学报，2011，15(6):97 -102.

［5］ GOLEA N，GOLEA A，NOUREDDINE M K.Robust MRAC adaptive control of PMSM drive under general parameters uncertainties［C］//IEEE International Conference on Industrial Technology.Mumbai，2006:1533 -1537.

［6］ MOHAMED Y A-R I.Design and implementation of a robust current-control scheme for a PMSM vector drive with a simple adaptive disturbance observer［J］. IEEE Transactions on Industrial Electronics，2007，54(4):1981 -1988.

［7］ WANG Song，SHI Shuang -shuang，CHEN Chao，et al. Research on grey compensation-prediction PID controller for PMSM servo system［C］//Chinese Control and Decision Conference，Xuzhou，China，2010:1425 -1429.

［8］ 孙海军，赵成明，李俊，等.灰色预测法PMSM 无传感器控制系统［J］.电机与控制学报，2007，11(6):604 -608.

［9］ MARUFUZZMAN M，REAZ M B I，ALI M A M.FPGA implementation of an intelligent current dq PI controller for FOC PMSM drive［C］//IEEE International Conference on Computer Appications and Industrial Electronics，Kuala Lumpur，Malaysia. 2010:602 -605.

［10］ QI Hui，ZHAO Ya.Design and realization of PMSM vector control IP core based on FPGA［C］//IEEE International Conference on Electrical Machines and Systems，Wuhan，China，2008:1325 -1328.