基于场路耦合的双余度永磁同步电动机特性仿真分析

周 勰，陈益广

(天津大学，南开300072)

0 引 言

永磁同步电动机与余度控制技术［1-7］相结合构成的双余度永磁同步电动机系统，既能发挥永磁同步电动机功率密度高、动态响应快、调速范围宽的优势，又能提高驱动系统的可靠性与安全性。

在双余度永磁同步电动机的控制系统设计和调试过程中，对其进行比较准确地仿真工作十分必要。许多学者在研究双余度电机方面已做了大量工作。Byung-Geuk Cho 和Vaseghi B 等对电机驱动电路的余度控制进行了深入研究［3-5］;周元军、马瑞卿等在Simulink 中建立了双余度电机数学模型和控制系统模型［6-7］，对双余度电机的运行特性进行了分析研究。但是，由于电机磁路饱和造成的非线性和转子磁场谐波的影响［8］，仅仅基于Simulink 的线性数学仿真模型不如基于有限元建立的电机本体模型准确。

本文以各相绕组间低热耦合无电磁耦合的双余度永磁同步电动机为研究对象，采用有限元分析软件Ansoft，建立电机2D 模型，应用Simulink 设计控制算法，再将Simulink 控制模型与Maxwell 电机模型以元件的形式载入到多领域联合仿真软件中进行场路耦合的联合仿真，从而更加接近于真实地观察双余度永磁同步电动机的运行特性，掌握其内部物理变化规律。

1 新型双余度永磁同步电动机建模

对于定子槽数为Z0转子极对数为p0的三相定子绕组采用双层分数槽绕组的永磁同步电动机，若定子槽数和永磁转子的极对数满足:

且Z0与p0之间无公约数，则称此电机为单元电机。

满足式(1)的单元电机，定子每π/3 空间上放置的属于同一相的偶数个线圈按正、反或反、正的顺序串联，使得各相绕组之间的主互感为0;但是，相邻的两相绕组会在6 个槽中共槽，共槽的分属两相的两个线圈边之间存在槽漏互感。这种单元电机各相绕组间存在电气耦合、较弱的电磁耦合和较强的热耦合。

若在上述单元电机相邻两相绕组存在共槽的6个槽中心各增设一个小齿，则各相绕组间总互感为0，各相绕组间既无电气耦合，也无电磁耦合;再在小齿两侧放置隔热板，使各相绕组的热耦合减弱。于是得到了各相绕组间低热耦合无电磁耦合的双余度永磁同步电动机，其截面示意图如图1 所示，其定子绕组展开如图2 所示。6 个相绕组按照A1，B2，C1，A2，B1、C2的 顺 序 排 布，最 后 连 接 成A1B1C1和A2B2C2两套Y 接三相对称绕组，两套绕组中相同冠名相的电动势同大小、同相位;两套绕组在空间上互补交叉布置，便于单余度运行时绕组铜耗的散热。两套绕组由两台逆变桥供电，正常时，双余度运行，两台逆变桥同时供电;当某一套系统的绕组或逆变桥发生故障时，进行余度切换，单余度运行，由另一套无故障系统供电。

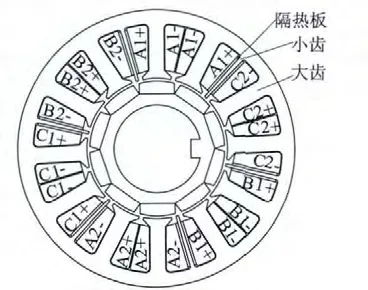
图1 双余度永磁同步电动机截面示意图

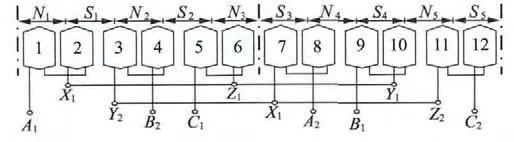
图2 双余度永磁同步电动机定子绕组连接图

定、转子铁心均为DW310 -35 硅钢片，永磁体是钕铁硼N35EH，平行充磁，充磁方向不等厚。线圈匝数为25，电机主要参数如表1 所示。

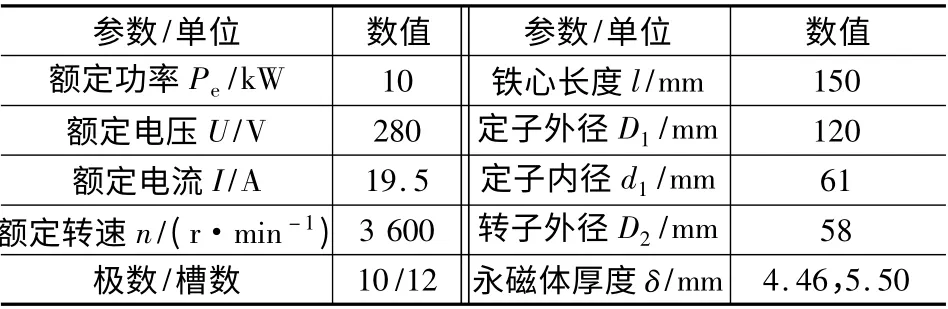
表1 双余度永磁同步电动机主要参数

依据上述参数在Ansoft 中建立起电机的有限元模型，通过静态磁场仿真得到该电机的电感参数矩阵列，如表2 所示。

表2 双余度永磁同步电动机电感矩阵参数

由表2 可知，各相之间的互感比相绕组的自感至少小两个数量级，可以忽略不计。由此也验证了该电机各相绕组之间互感为0，无电磁耦合的特点，两套绕组在电气和电磁上是相互独立的。由表2 可计算得到两套Y 接三相绕组的交、直轴电感为2.07 mH。

2 双余度永磁同步电动机控制系统建模

假设功率开关器件特性一致，忽略永磁体充磁方向不等厚带来的转子位置变化对电感参数的影响，认为交、直电感相同且等于各相绕组的自感L，各相绕组电阻为R。两套绕组在电磁效应完全一样，暂时忽略磁路饱和的影响，可以得到其定子双三相静止坐标系下的磁链方程和电压平衡方程:

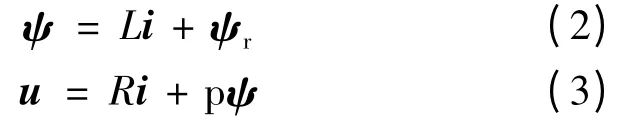
其中:

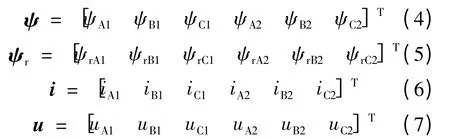
式中:下标i =1，2 用于标注两套Y 接三相绕组;ψAi，ψBi和ψCi为各相绕组交链的全磁链;ψrAi，ψrBi和ψrCi为各相绕组交链的永磁磁链;iAi，iBi和iCi为各相绕组的电流;uAi，uBi和uCi为各相绕组的电压;p 为微分因子。

通过Clarke-Park 变换，得到双dq 转子同步旋转坐标下的磁链与电压平衡方程:

式中:ψrm为转子永磁磁链峰值;ωe为三相交流电源的角频率。

dq 转子同步旋转坐标系下的电磁转矩方程与机械运动方程:

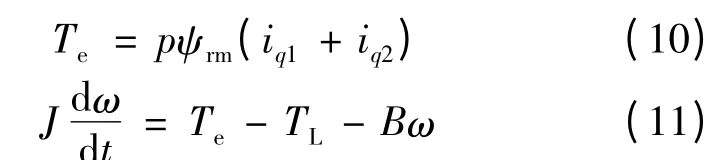
式中:Te为电磁转矩;p 为电机极对数;J 为转子集总转动惯量;ω 为转子机械角速度;TL为负载转矩;B 为粘滞系数。

由式(9)和式(11)进行拉普拉斯变换，得:

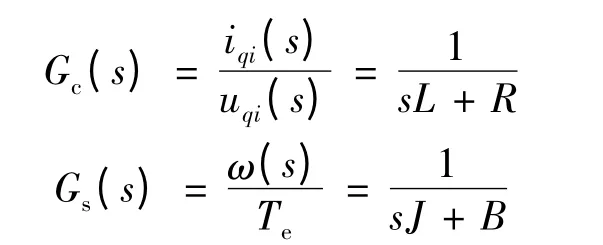
设转矩系数、反电动势系数分别为Kt，Ke，且:

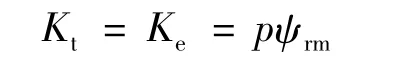
设GASR(s)，GACR(s)分别为采用PI 调节的速度调节器与电流调节器的传递函数，且:

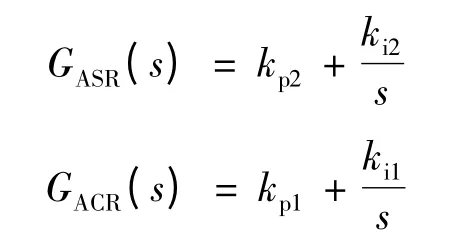
双余度永磁同步电动机的控制系统框图和结构框图分别如图3 和图4 所示。

图3 双余度永磁同步电动机的控制系统框图

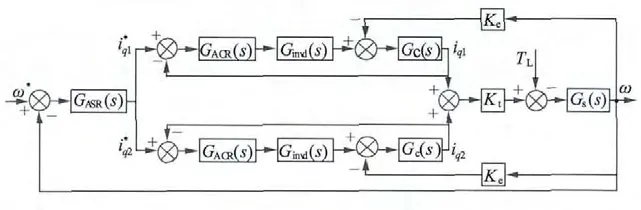
图4 双余度永磁同步电动机控制系统结构框图

图4 中，Ginvd(s)表示SVPWM 逆变的传递函数［9］，由于逆变的传函只对高频有较大影响，对系统中、低频响应特性影响很小，可忽略不计。由此可得电流环的开环传递函数［9］:

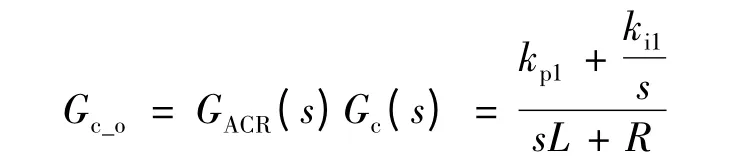
其中:kp1=ωcL;ki1=ωcR。

由式(12)可知，额定转速时电角频率为1 885 rad/s，为了既能快速响应，又保留足够的相角裕度，取ωc=2 500 rad/s，于是得到电流调节环的PI 参数，如表3 所示。

同样可得速度环的开环传递函数:

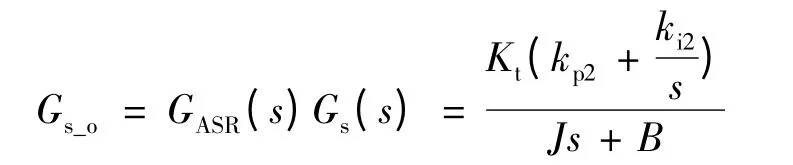
取额定角频率ωs=377 rad/s，转矩系数Kt=0.468，集总转动惯量J =9.13 ×104kg·m2。可以计算得到kp2=0.74，为了满足快速性、消除稳态静差，同时避免对电流环形成串扰，ki2取240，两个调节器的参数取值如表3 所示。

表3 电流调节器与速度调节器参数

在Simulink 中建立采用id=0 控制策略的双余度永磁同步电动机双闭环SVPWM 矢量控制模型［9-10］，如图5 所示。其中Control1、Control2 分别为内含电流调节和SVPWM 控制的两套绕组的电流控制模块，其构成如图6 所示。

图5 双余度永磁同步电动机矢量控制系统模型

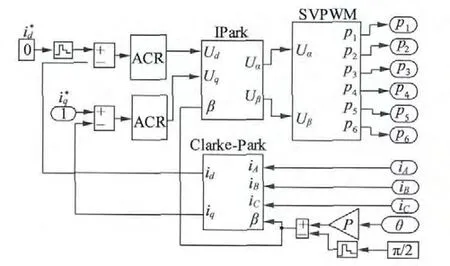
图6 内含电流调节和SVPWM 控制的电流控制模块

采用平均电流法［11］实现两套绕组的电流均衡，即将速度调节器的输出经限幅后作为两套绕组的q轴电流给定，避免出现电流不均衡以及由其所而引发的转矩纷争。在图5 中右半部分还构建了一个s函数Ansoft SFunction，该函数用于Simulink 模型与电机有限元模型进行耦合，仿真参数设置如表4 所示。

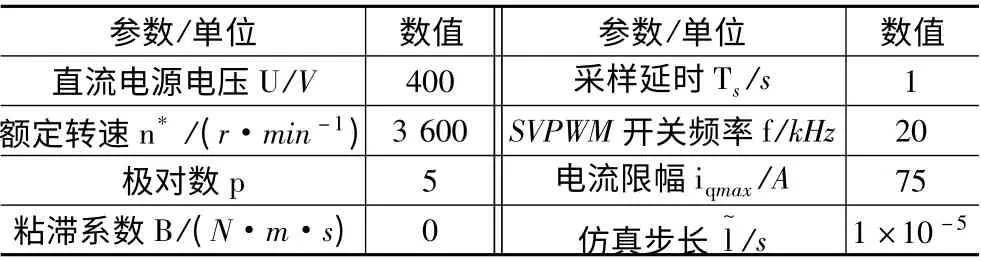
表4 Simulink 中控制系统模型参数

3 联合仿真

在场路耦合软件中，将双余度永磁同步电动机的有限元模型与Simulink 控制系统模型以元件的形式载入，建立如图7 所示的联合仿真。

图中左半部分是两个三相逆变桥。采集有限元电机模型瞬态仿真时两套绕组的各相电流、转子位置角和转速，反馈到Simulink 中完成均流、速度调节、电流调节的矢量控制;通过Simulink中的SV -PWM 脉冲信号控制IGBT 的导通与关断实现两套绕组的电流控制，从而控制电机有限元模型的瞬态仿真。联合仿真时间及仿真最大步长分别设置为40 ms、20 μs，且均与电机的有限元瞬态仿真模型保持一致。

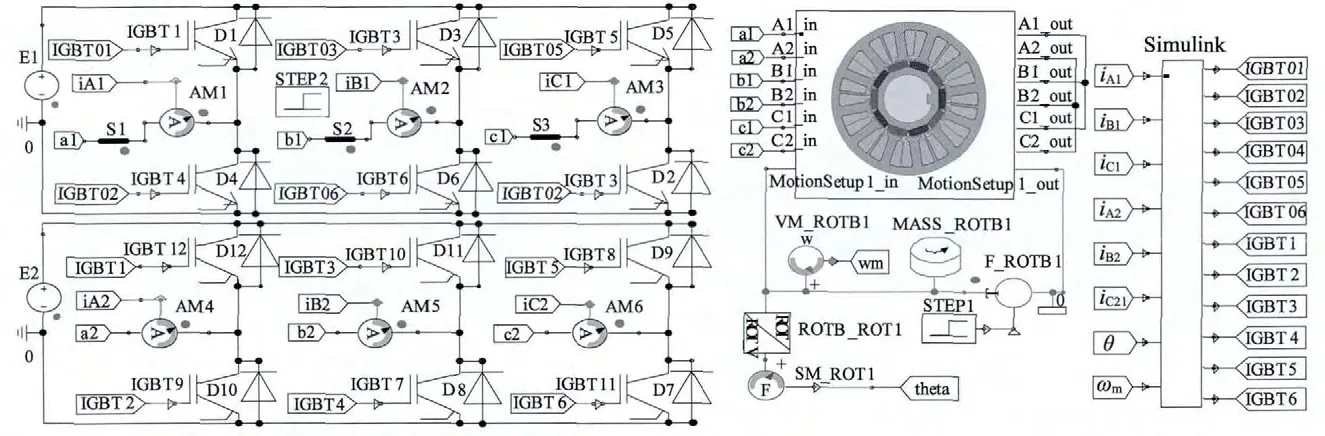
图7 双余度永磁同步电动机SVPWM 矢量控制联合仿真图

3.1 空载及额定负载运行时的特性仿真

电机空载起动，在23 ms 时刻突加额定转矩26.5 N·m，仿真后得到的电流、转速、转矩波形如图8 所示。由于两套绕组仿真模型参数一样，两套绕组的电流波形一样，突加负载稳定后，电流峰值为27.80 A，有效值为19.66 A。由图8 可见，起动过程，速度超调67 r/min，为额定转速的1.86%，经过12 ms 起动过程结束。突加负载后，经过2 ms 恢复到给定转速，说明速度调节器参数设置较合理;电机额定负载稳定运行时电流波形正弦性较好，说明电流调节器的参数设置也比较合理。

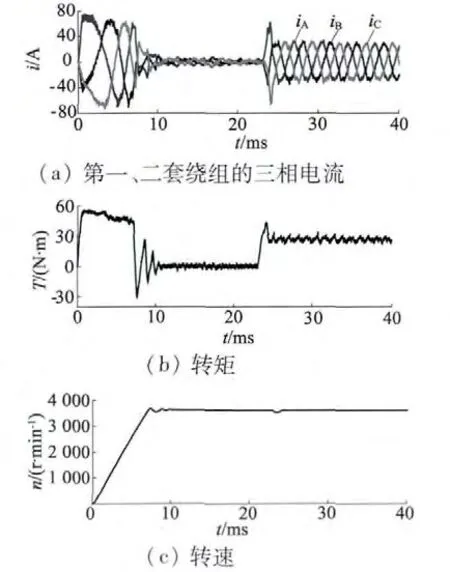
图8 空载起动及突加额定负载运行仿真结果

3.2 带0.7 倍负载实现余度切换时的运行特性

当双余度永磁同步电动机出现一套绕组断路或匝间短路等故障时，为了防止故障的进一步扩大，影响另一套健康绕组，在判别出故障绕组后，须将故障相所在那一套绕组全部切除，实现单余度运行。为了避免健康绕组过度发热，此时双余度永磁同步电动机须降额带0.7 倍额定负载，定子铜耗才与双余度运行时相当，电机才能长期安全运行。

仿真时，电机空载起动，在15 ms时刻突加18 N·m 的负载转矩，在25 ms 时刻利用定时开关断开第一套绕组，电机内部只有第二套绕组单独工作，仿真结果如图9 所示。

图9 带0.7 倍额定负载实现余度切换运行的仿真结果

由图9 可知，25 ms 时刻突然断开第一套绕组，此后该套绕组的感应电压变为永磁感应电动势。实现余度切换后，电磁转矩突然减少，转速下降;但是，在控制系统的调节下，第二套相绕组感应电压也明显增大，第二套绕组电流迅速增加，转矩重新达到平衡，转速重新恢复到给定，电机依然能够平稳运行。稳定运行时，第二套绕组电流显著变大，峰值由原来的19.14 A 变为40.15 A，有效值从13.53 A 变为28.39 A。忽略电阻随温升的影响，实现余度切换后绕组的铜耗约为余度切换前绕组铜耗的2.19 倍，是双余度带额定负载运行时铜耗的1.04 倍，电机仍能长期安全运行。这也说明受磁路饱和影响，单余度工作时，随着电枢电流的增加，电磁转矩增加变缓。这也是双余度电动机单余度长期工作时只能够带0.7 倍额定负载运行的原因。

4 结 语

本文对各相绕组间低热耦合无电磁耦合的新型双余度永磁同步电动机在正常工况下的运行特性进行了场路耦合的联合仿真，并对仿真结果进行了分析，仿真结果与理论相符。由于有限元电机模型考虑了磁路饱和造成的非线性和转子磁场谐波的影响，比单纯的Simulink 数学模型更加准确，能够更真实地反映电机的运行特性，为实际控制系统参数的设计和进一步优化提供了参考。

［1］ 王慧娟. 双余度电动伺服舵机系统设计［D］. 南京:南京航空航天大学，2010.

［2］ 高金行，戴志勇，全兴源，等. 舵机用双余度无刷直流电动机设计研究［J］. 微特电机，2011，39(12):13 -15，25.

［3］ CHO B - G，YOON Y - D，SUL S - K，et al. A separate double winding 12 -phase brushless DC motor drive fed from individual H-bridge inverters［C］//Energy Conversion Congress and Exposition，Atlanta，GA，2010.

［4］ VASEGHI B，TAKORABET N，Caron J P，et al. Study of different architectures of fault- tolerant actuator using a two-channel PM motor［J］. IEEE Transactions on Industry Applications，2011，47(1):47 -54.

［5］ MONDAL G，SIVAKUMAR K，RAMCHAND R，et al.A dual sevenlevel inverter supply for an open-end winding induction motor drive［J］. IEEE Transactions on Industrial Electronics，2009，56(5):1665 -1673.

［6］ 周元钧.双绕组无刷直流电动机的数学模型与转矩特性［J］.电工技术学报，2004，19(4):12 -16.

［7］ 马瑞卿，刘卫国，杨永亮.双余度无刷直流电动机的建模与余度控制技术［J］.微特电机，2008，36(7):32 -35.

［8］ 刘仕钊，宋琼，舒杨，等.考虑转子磁场谐波的永磁同步电动机仿真［J］. 微特电机，2013，41(9):17 -19.

［9］ 王莉娜，朱鸿悦.永磁同步电动机调速系统PI 控制器参数整定方法［J］.电工技术学报，2014，29(5):104 -117.

［10］ 洪熙闻，王钦若.永磁同步电机电压空间矢量控制仿真研究［J］.上海大中型电机，2010，(4):43 -47.

［11］ 林辉，戴志勇，马冬麒.双余度舵系统中的电流均衡策略研究［J］.微特电机，2012，40(4):10 -15.