基于遗传算法的铁路技术站取送车计划研究

薛玉玺，朱海笑，甘　宝，韩瑜睿

(兰州交通大学　交通运输学院，甘肃　兰州　730070)

基于遗传算法的铁路技术站取送车计划研究

薛玉玺，朱海笑，甘宝，韩瑜睿

(兰州交通大学交通运输学院，甘肃兰州730070)

薛玉玺(1990—)，硕士研究生，研究方向：交通运输规划与管理；

朱海笑(1989—)，助理工程师，研究方向：客运组织管理；

甘宝(1989—)，硕士研究生，研究方向：交通运输规划与管理；

韩瑜睿(1990—)，硕士研究生，研究方向：交通运输规划与管理。

摘要：为了研究更切合实际的铁路技术站取送车计划的合理编制方案，文章在考虑调机牵引能力、装卸线容车限制的约束下，以取送照顾编组为前提，在取送控制时间窗内，对站存车组及陆续到达车组的取送优化建立了以调机取送成本最小为目标的概念模型，并采用改进的遗传算法求解。通过算例求解，验证了该模型的正确性和算法的有效性。

关键词：取送车；时间窗；放射性专用线；遗传算法；整数编码

0引言

在我国，铁路运输有着极其重要的地位，因此有大量专门针对铁路取送车作业的研究。马许教授[1]率先提出了取送调车的概念，为取送车问题这一新的研究领域提供了最初的理论基础。李文权和杜文[2]针对组织装车地始发直达列车的树枝状车站，建立了图论模型，考虑取出车辆配合运行图发车时间以及机车作业和装卸作业的协调问题，建立了机器加工的排队模型。徐忠民、孔庆钤[3]对直达车流取送顺序问题的原理进行了分析，提出调机中断时间最小的方案即为最优方案，并改善了求解的效率。

大多文献都简化了取送问题，如假定车辆行驶时间及装卸时间确定，调机牵引能力和装卸线能力充分等，而这些都与实际生产不相符。本文在前人研究的基础上，从实际出发，将取送问题看作一个整体进行研究，从理论和方法两方面优化取送车作业，使之与车列的解体和编组紧密配合。

1取送车问题的概念模型

由于取送车问题同时涉及时间和空间两个方面，变量较多，比较复杂，并且数学解析模型难以同时描述时空约束，因此考虑建立概念模型。

1.1　变量及含义说明

为描述模型和构造解的方便，设定如下变量：

(1)对取送作业按类型编号，记为k，k=1，2，3分别表示送车、取车、专用线留存车组的取车。

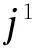
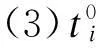
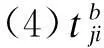
(5)Tji：车组ji货物作业时间，min。

(6)Tj：车站至专用线j的单程走行时间，min。

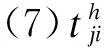
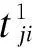
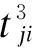
(10)用s表示某一车组的一项作业，设共有n项工作，送车和取车各算一项工作，一个编号唯一对应一个车组的一项工作，从而s=1，2，…，n。

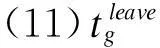
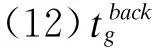
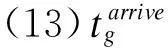
(14)调机送车包含挑选车组、对货位，取车包含收集车辆和分解车组的工作，用t0表示在车站内的消耗时间，t1表示在专用线上消耗的时间。

(15)M：调机最大牵引能力。

(16)B：计划阶段总时间。

(17)e0：调机的单位小时取送成本；e1：超过时间后的单位小时惩罚成本。

(18)y0：调机实际的总工作时间。

(19)y1：调机实际工时y0与B的差值，y1=y0-B，y1>0说明调机实际工时超过该计划时段，y1≤0说明没有超过。

综上，每一项作业都有一个编号s，而每个编号都唯一对应一个数组：

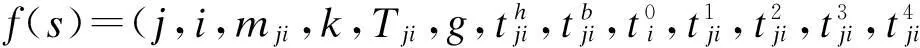
调车作业需要满足一定的时间窗约束，现推导不同工作的取送控制时间窗：

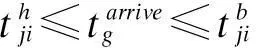
对于专用线既有车组，上述两个取车控制时刻已知，而计划阶段内从车站送入专用线的车组，仅知道最晚取车时刻，而货物作业时间需要送入时刻来计算。未规定挂运车次的任何一种取车车组，取车只需在货物作业完毕之后，同理最晚编组时刻=∞。

1.2　概念模型的建立

(1)解的形式

对于每一项工作，都有一个唯一的编号s与之对应，可用编号s的序列来表示取送顺序，显然s是随机编排的，因此问题的解可以表示为X=s1s2s3…sn，其中的每一个su(u=1，2，…，n)代表一项工作，u是该工作在这个方案中的顺序。

该编码方式虽然不能一眼看出调机工作内容，但易于解码还原，可以用遗传算法来求解。每一个编码都唯一对应一个问题的解，任意解都对应着一个编码，这些都符合编码的不冗余性、合法性和完备性要求，且利于遗传算法求解时的操作。

(2)方案值计算函数

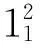
函数1批次划分函数

根据相异放射枝不同批约束条件，判断某个方案中相邻的两项取送作业是否可以划分为同一批次。所谓相异放射枝不同批约是指：两项相继完成的取送作业如果对应于不同放射枝，则不属于同一批次。

函数2每批作业取送车数计算函数

对已经划分批次的取送作业方案，求得每一个批次的取送作业中，调车机车所牵引的车辆数，包括送车作业的车辆数和取车作业的车辆数，并将其值返回主调函数。

函数3调机牵引能力判断函数

判断每一批次的取送作业中，调车机车所牵引的车辆数是否超出了机车的最大牵引能力M，若超出给主调函数返回0，否则返回1。

函数4专用线容车限制判断函数

判断某批次的行车作业中，调车机车牵引的车辆数加上专用线原有的车辆数是否会超出专用线的容车能力限制，若超出给主调函数返回0，否则返回1。

函数5取送时刻判断函数

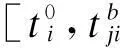
函数6方案值计算主函数

输入：解序列

Step1：剔除不合理方案，同一车组先取后送的方案不可行，将该解放入第一类不可行解集合内，结束；否则转step2。

Step2：调用函数1，对初始解划分批次，记录最大批次max g；对每个批次判断批次规模Bg。

Step3：调用函数2，计算每批次的送、取车数。

Step4：调用函数3，判断每批次是否超过调机牵引能力；若未超出转step6；否则，将该初始解放入第二类不可行解集合内，结束。

Step5：调用函数4，判断每批次是否超过专用线容车量；若未超出转step7；否则，将该初始解放入第二类不可行解集合内，结束。

Step6：调用函数5，判断取送作业时刻是否满足时间窗，并记录每批作业的离站时间和返站时间；若满足转step8；否则，将该初始解放入第三类不可行解集合内，结束。

Step7：计算调机总取送时间y0。

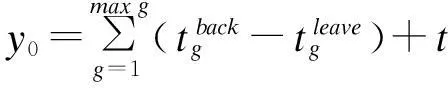
y1=y0-B；

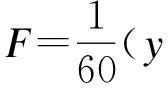
3算法描述及改进

由于遗传算法本身的高度并行、随机、自适应等优点，本文用改进的遗传算法求解。

(1)初始群体的产生

由于取送车问题的约束条件多且时间要求苛刻，可行解较少，所以选用改进方法来产生初始群体。本文中染色体X=s1s2s3…sn，每一个su代表一个基因，u是该基因在整个染色体中的位置，也是工作顺序，su的取值范围是[1，n]。在每个基因位随机产生编号时，对前r个基因位的取值给定一个范围，来保证靠后时段的作业编码不会在靠前位置。通过这种优化，就能很快产生N个可行解。

(2)交叉操作

交叉操作用于组合出新的个体，并使算法能够搜索更多的解[4]。本文中选择部分映射交叉。先任选两个交叉点，交换两个个体交叉点之间的基因片段，对于原有基因，如果与交换过来的基因片段不冲突则保留，否则通过映射来找交换所得基因原位置的基因，直到没有冲突基因为止。

(3)变异操作

变异操作可以扩大算法的搜索范围，经过变异的染色体将成为一个全新的个体，操作之前会赋予每一个基因一个相对较小的变异概率。组合优化问题中一般会采用互换、逆序和插入变异[5]。本文中，算法的优化主要就是通过变异操作，将各类不可行解调整为可行解。

第一类是同车组取车作业在送车之前的，采用

互换变异，将送、取作业颠倒变为可行方案；第二类是不满足调机、专用线容量限制采用随机互换变异，将大规模的批次分开作业，使其满足约束，成为可行解；第三类是不满足最晚编组时刻，采用向前插入变异，即将该工作的顺序提前从而满足时刻，成为可行解。

(4)选择和替换操作

本文中：不可行解直接变异产生新个体；可行解用轮盘赌的方法选择优秀个体交叉变异产生新个体，二者共同产生N-a个新个体，并保留父代中较好的前a个个体，这样共产生N个子代。

(5)算法终止条件

遗传算法理论上能以概率1收敛到最优，但实际中很难实现，因此实际中通常求得具有一定质量的满意解。常用的终止规则有：给定最大遗传迭代步数、给定最佳搜索解的最大滞留步数、给定问题的下界和一个偏差度，若当前最优解与下界的差不大于偏差度时停止运算[6]。本文采取最大迭代步数终止法。

4算例分析

以连接4条放射形专用线的铁路技术站为例，各专用线的调机走行时间及需取回车组的各时刻信息如表1所示，陆续到达的各趟列车包含的车组信息如表2所示。M=30车，B=720 min，t0=t1=10 min，e0=18元/h，e1=6元/h，现需确定调机的作业顺序及批次信息。

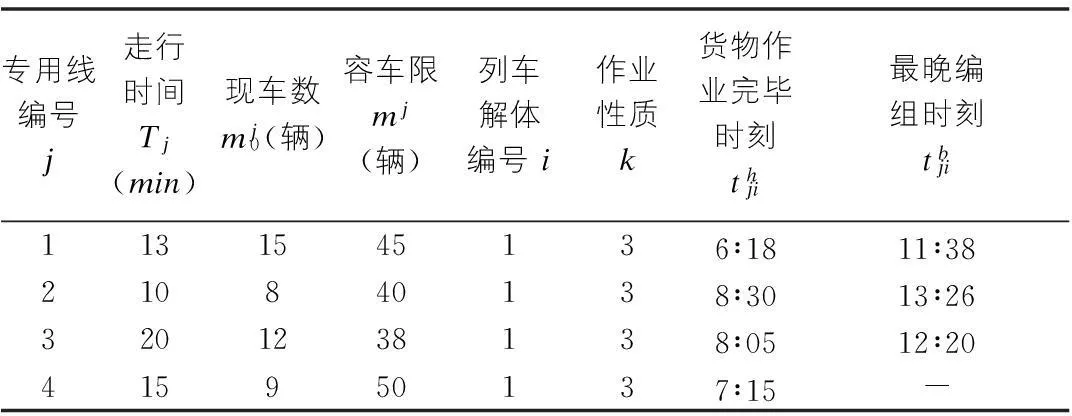
表1　专用线车组信息表

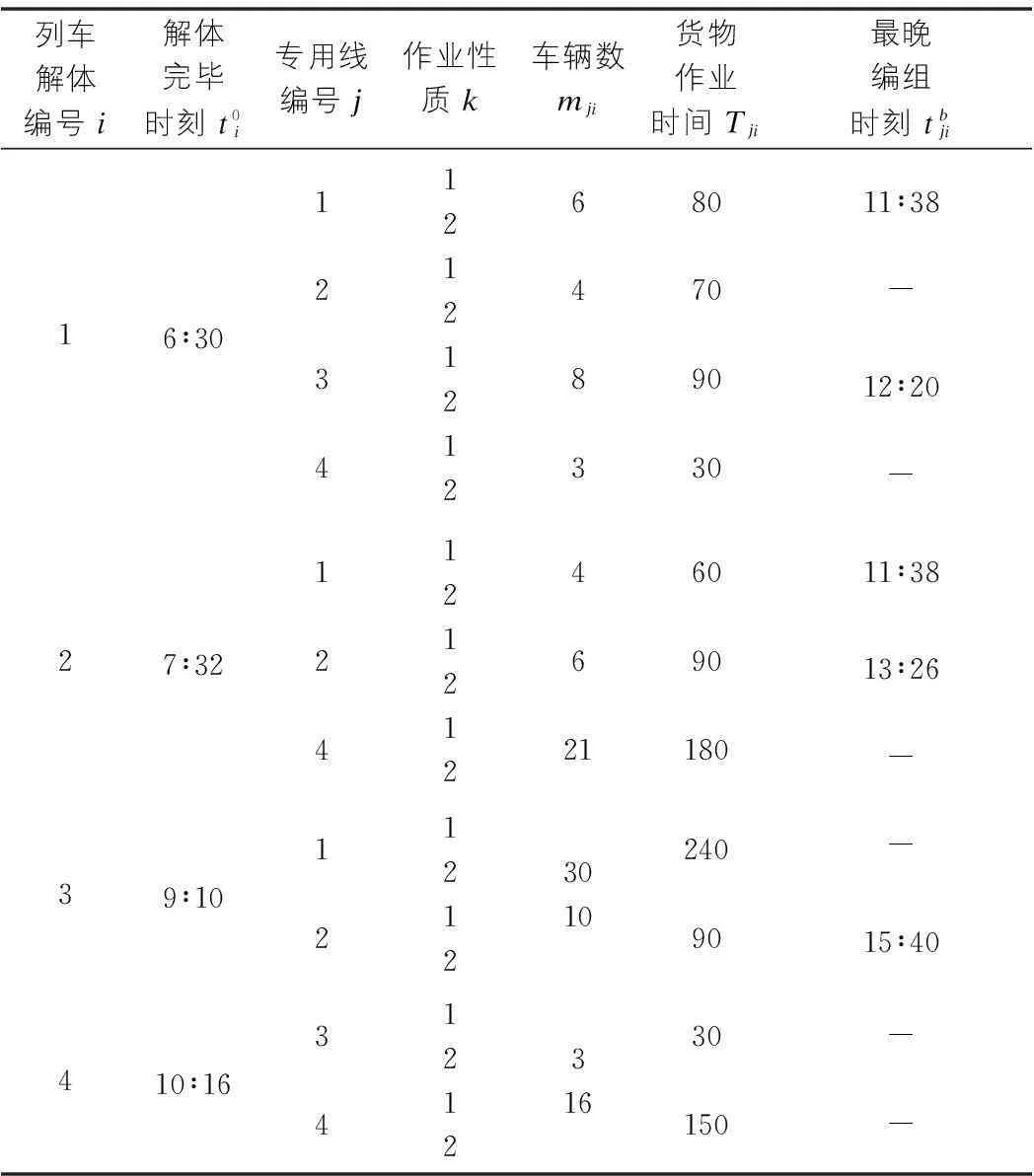
表2　到达车组信息表

首先需要按照时段对各作业编上唯一的编号，如表3所示。

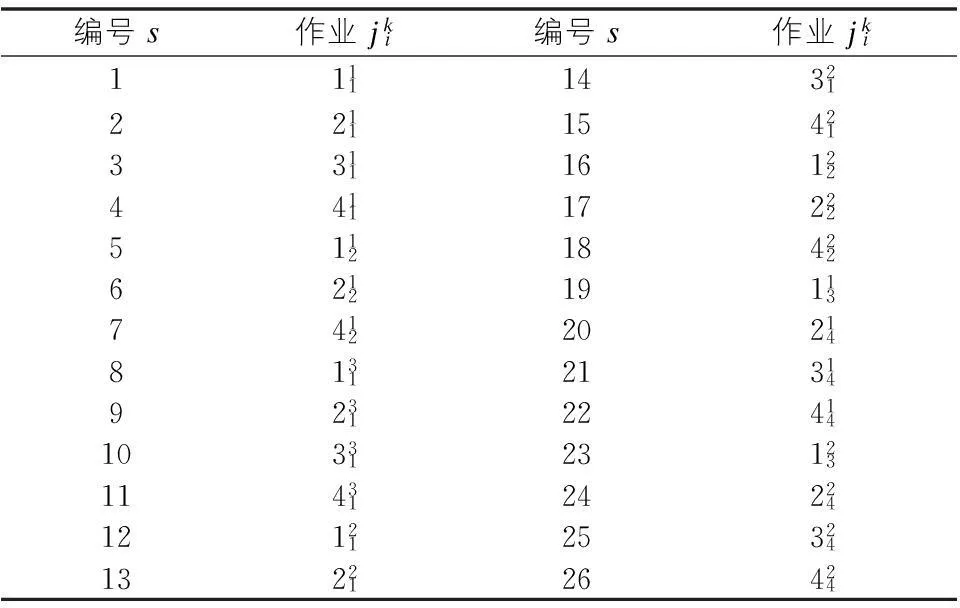
表3　工作编号表

(1)对上述案例采用C++语言编写的遗传算法求解，编译环境为CodeBlocks13.12，运行环境为RAM4G，CPU2.53 GHz，计算时间为8 s左右。将案例内各时间转换为十进制数，以6：00为起点0，各参数设置为N=100，pc=0.85，pm=0.03，保留父代较优的10个个体，最大迭代步数为500，所得满意解解码如下：

X1=1531281620621410139172471921252218411231526

X2=1531281620621410139172471921252241811231526

两等值方案中，虽然调机最终的取送离站与返站时间相同，但方案2少一个批次，从调机能耗方面显然优于方案1，之所以全部取送完成返站时间相同，是方案2在1专用线等取车组23。

实际作业时，可以进行调整，让调机在做完第10批作业以后，可以先做取送以外的调车工作，如辅助解体、编组等，在第686 min时开始第11批作业，达到1专用线时车组23刚好作业完毕取回，然后紧接着做第12批作业。调整以后取送调机多出近1 h时间辅助其他调机作业，合理利用了调机能力，加强了各作业间的协调配合。调整前调机总取送工作时间678 min，成本是203.4元，调整之后总取送时间为624 min，总取送成本187.2元。因此，现场操作时，可以按照表4所示时间及内容进行取送作业。

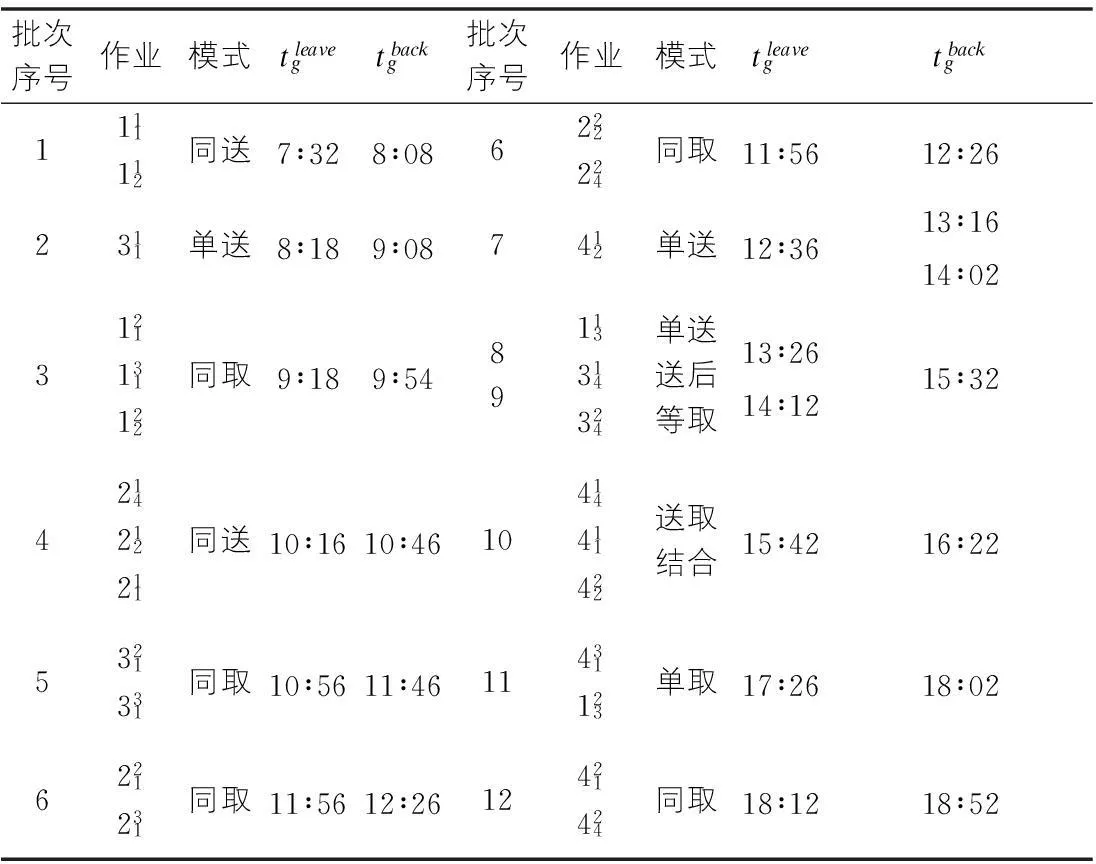
表4　取送批次及时机数值表

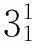
计划时段起始时间为6：00，而第一批作业开始时间为7：32，另外第10批和第11批作业之间也有空闲时间，取送调机可以辅助其他调机作业。

5结语

本文分析了放射形专用线非直达车流的取送车流程，从取车照顾编组的角度，利用取送车控制时刻的概念，考虑了调机牵引能力及专用线装卸区的容车约束，建立了以调机取送成本最小为目标的概念模型。优化后的解不仅包括取送顺序还自动划分了批次，使取送顺序、时机与批次得到统一，以调机取送成本最小为目标的优化，会使取送作业计划尽量以较少的批次完成所有作业，充分利用调机与装卸线的能力，更加经济合理。

论文虽然做了一定的改进，但依然存在很多需要改进和完善的地方：

(1)在建立模型的假设中，将调机的走行时间假设为定值，不符合实际。

(2)为了简化，超过调机或装卸线能力限制就全部不送或不取，与实际情况有些出入。

(3)本文采用了常用的遗传算法求解模型，并没有与其他智能算法相比较或相结合，因此不能说明该算法是最优的，只能说明其有效性。所以算法方面需要更深入地研究。

参考文献

[1]马许.车站与专用线在统一技术作业过程中相互配合条件之研究[C].北京铁道学院第一次科学讨论会论文选集(铁道运输部分)，1956.

[2]李文权，杜文.树枝状铁路专用线取送车问题的数学模型及算法[J].河南大学学报(自然科学版)，1997，27(2)：11-8.

[3]徐忠民，孔庆铃.直达列车取送车顺序的优化[J].北方交通大学学报，1988.2：70-74.

[4]曾凡超.车辆路径问题的改进遗传算法[D].重庆：重庆大学，2007.

[5]占焱发.基于遗传算法的物流配送车辆路径问题研究[D].西安：长安大学，2010.

[6]玄光男，程润伟.遗传算法与工程优化[M].北京：清华大学出版社，2004.

Research on Vehicle Pick-up and Return Plan of Railway Technical Station Based on Genetic Algorithm

XUE Yu-xi，ZHU Hai-xiao，GAN Bao，HAN Yu-rui

(School of Traffic and Transportation，Lanzhou Jiaotong University，Lanzhou，Gansu，730070)

Abstract：In order to study more realistic and reasonable preparation for vehicle pick-up and return plan of railway technical station，then under the constraints of considering the machine towing capacity of and vehicle capacity limitations of loading/unloading lines，with the priority pickup and return grouping as the premise，and within the pickup/return control time window，this article established the concept model for the pickup/return optimization of vehicle groups stored in the station and vehicle groups arriving with the minimum machine pickup/return cost as the goal，and used the improved genetic algorithm for the solu-tions.Through the solutions of numerical examples，it verified the correctness of this model and the va-lidity of this algorithm.

Keywords：Vehicle pick-up and return；Time window；Radioactive dedicated line；Genetic algorithm；In-teger coding

文章编号：1673-4874(2015)12-0053-05

中图分类号：U292.2+9

文献标识码：A

DOI：10.13282/j.cnki.wccst.2015.12.013

作者简介

收稿日期：2015-11-18