饱和铁心型超导限流器的暂态特性分析

何健，郭丰瑞

(1.中国能源建设集团广东省电力设计研究院有限公司，广州市 510663；2.国网天津市电力公司，天津市 300072)



饱和铁心型超导限流器的暂态特性分析

何健1，郭丰瑞2

(1.中国能源建设集团广东省电力设计研究院有限公司，广州市 510663；2.国网天津市电力公司，天津市 300072)

随着电网规模的不断扩大，短路电流超标问题已成为制约电网负荷增长和电网发展的突出因素之一。传统的限流措施已经很难满足现代电力系统发展的需要，随着超导材料的快速发展，超导限流器这种利用新兴超导技术而研制出的快速有效的限流装置应运而生。由于饱和铁心型超导限流器拥有突出的优越性能，其被广泛应用于输电线路及配电系统中。考虑到饱和铁心型超导限流器的实际结构，提出了一种新式等效磁路法，进而可以精确、有效地分析限流器的暂态特性。等效磁路法的提出对饱和铁心型超导限流器的理论分析及实际应用都有重要的意义。

饱和铁心型超导限流器；电磁暂态分析；等效磁路法；牛顿迭代

0 引 言

随着电网规模的不断扩大，短路电流超标问题已成为制约电网负荷增长和电网发展的突出因素之一。在欧美及发达国家和国内都是如此，特别是近些年在国内的广东电网。近年来，随着电网的装机容量和各电压等级网架建设得到高速发展，500 kV网架结构大大加强，很多地区基本形成双回路内外环网结构。电网满足了电网负荷增长和可靠供电的需求，但同时也使电网的短路容量持续增长。虽然电网已采取优化电源布局、调整电网结构、合理安排运行方式(分区供电、母线分段运行)、采用传统限流设备(高阻抗变压器、加装变压器中性点小电抗)等措施来抑制和降低电网的短路电流水平，但也不同程度降低了电网运行的可靠性和灵活性[1]。

超导限流器是利用新兴的超导技术而研制出的快速有效的限流装置[2]。饱和铁心型超导限流器(saturated iron-core superconductive fault current limiter，SISFCL)[3]：如图1所示，其由一对铁心组成，每个铁心有铜的交流限制绕组以及直流超导绕组。2个交流限制绕组极性相反地串联，直流超导绕组串联并加直流偏压源。正常运行时，调节直流偏压源使2个铁心饱和，呈现低阻抗。当线路故障时，短路电流使2个铁心在1个周期内交替去饱和，从而产生很大的电抗以限制短路电流。由于饱和铁心型超导限流器的超导线圈始终维持在不失超的状态，因此其不存在失超恢复时间，可以在故障发生后迅速响应，并且饱和铁心型超导限流器具备多次自动启动功能，从目前的技术水平看，适于自动重合闸运行。且饱和铁心型超导限流器从正常运行向故障状态转变是渐进的，产生的过电压小[4]。饱和铁心型超导限流器采用了松耦合设计，分离限流器的高压(交流绕组)和低压(直流绕组和铁心其他部分)，使整体结构更紧凑，在体积、质量、消耗材料等方面都有较大改进。直流超导电缆绕组制作比较容易，制成的限流器体积小。饱和铁心型超导限流器优点众多，具有无可比拟的优势，是未来限流器的发展与应用方向。

图1 饱和铁心型超导限流器Fig.1 The saturated iron-core superconductive fault current limiter (SISFCL)

由于超导限流器在电力系统的应用越来越广泛，因此有效、精确的仿真模型对于其理论分析及实际应用都有重要的意义[5]。现在国内外对超导限流器仿真有一些方法，例如时域分析法、基于等效磁路法的非线性电感实现及有限元分析法等[6-8]。以上仿真方法都存在自身的缺陷，时域分析法、基于等效磁路法的非线性电感实现只能分析超导限流器的理论模型，即铁心各处截面积相等[9]。但实际应用时，饱和铁心型超导限流器往往采用铁心不等截面积设计，即直流侧铁心截面积大于交流侧铁心，使直流侧铁心中的磁通更多地输送到交流侧铁心，从而有效地保证交流铁心的过饱和程度。有限元分析法可以有效分析超导限流器自身的电磁暂态特性，但是其与实际电网耦合度较差，无法准确分析超导限流器接入输电线路时对系统的影响[10]。因此本文针对饱和铁心型超导限流器的实际应用结构，提出一种新式的等效磁路法，可以有效、精确地研究超导限流器自身及其接入输电线路后的电磁暂态特性。

1 饱和铁心型超导限流器及其磁路分析

1.1 饱和铁心型超导限流器工作原理

饱和铁心型超导故障限流器的基本原理如图1所示。其由铁心、常规交流绕组、直流超导绕组3个部分组成[11]。其中铁心由2个“口”字形铁心组成，交流绕组为2个常规导体绕制的线圈，串联在电网中，分置于不同的铁心上，线圈产生的磁场方向相同；直流绕组为超导材料绕制而成，为2个铁心提供直流励磁。

图2为被动式饱和铁心型超导限流器的工作模式[12]。正常运行时，直流电源为超导绕组提供励磁电流，产生一个偏置磁场，使铁心处于深度饱和状态，铁心工作于工作点HDC。此时，额定的交流电流通过交流绕组线圈所产生的交流磁场不足以使铁心脱离饱和区，铁心内的磁通量几乎不变，根据法拉第电磁感应定律，交流绕组的感应电动势为0，即超导限流器两端电压为0。此时铁心磁导率处于较低水平，即铁心等效电感较低，说明此时超导限流器对系统基本无影响。当短路故障发生时，短路电流大大增加，使铁心脱离饱和区进入非饱和区，此时铁心磁导率迅速增大，使得超导限流器的限流阻抗呈现较大值，从而自动限制了电网的短路电流。从根本上说，饱和铁心型超导限流器是利用铁心材料磁导率的非线性变化来限制短路电流[13]。

图2 饱和铁心型超导限流器工作原理Fig.2 The working principle of saturated iron-core superconductive fault current limiter

同时，被动式饱和铁心型超导限流器采用了两级铁心，短路电流迫使2个铁心在1个周期内交替退出饱和，由此可以在正半周和负半周分别限制短路电流。显然，对于用作限流器的铁心，其磁化曲线的饱和区和非饱和区的区分越明显越好，饱和区越平缓越好，这样正常工作时绕组的电压降越小，对系统的影响越小。超导绕组体所起的作用是无阻承载直流偏置电流，提供更大的直流磁化场克服交流磁化场，使得铁心处于深度饱和状态。

1.2 饱和铁心型超导限流器等效磁路分析法

在实际电力系统的应用中，饱和铁心型超导限流器采用三相合一结构，然而考虑到设备绝缘及电力系统操作要求，超导限流器实际由3个独立的单相限流器组合而成。每一相限流器主要由铁心、2个交流绕组和1个直流超导绕组构成，其中铁心由直流中柱、轭铁、交流边柱组成，下面将针对单相超导限流器的结构，对其等效磁路法进行分析研究。

超导限流器单相结构示意图如图3所示。因2个中柱之间的气隙有几cm，所以可以认为2个铁心分别为2个独立的磁路。实际超导限流器铁心采用了不等截面积设计，所以其等效磁路如图4所示。由于3个独立的单相超导限流器电磁暂态过程相同，因此这里我们仅以一相为例加以说明。

图3 单相超导限流器铁心结构示意图Fig.3 Iron structure of single-phase superconducting fault current limiter

由图3所示，2个铁心直流中柱间存在几cm的气隙，因此可认为超导限流器由2个独立的磁路C1和C2组成。由图4所示的超导限流器的各物理量以及正方向，根据基尔霍夫第二定律[14]，两磁路C1和C2的磁动势分别满足式(1)和(2)：

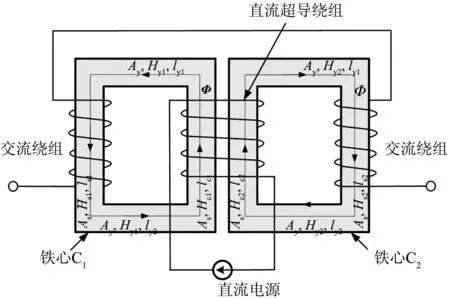
图4 超导限流器铁心等效磁路示意图Fig.4 Equivalent magnetic circuit of iron core of superconducting fault current limiterHs1ls+Hy1ly+Hc1lc=Naciac+Ndcidc=F1

(1)

Hs2ls+Hy2ly+Hc2lc=Naciac-Ndcidc=F2

(2)

式中：ls、ly(ly=ly1+ly2)和lc分别为交流边柱、轭铁和直流中柱的中心线长度；Hs1、Hs2、Hy1、Hy2、Hc1、Hc2分别是磁路C1和C2的交流边柱、轭铁和直流中柱的磁场强度；Nac和Ndc分别是交流绕组及直流绕组的匝数；iac和idc分别为交流绕组及直流绕组的电流大小。

根据等效原则，将励磁电流折算到直流侧，并且令

Naciac+Ndcidc=Ndciμ1

(3)

Naciac-Ndcidc=Ndciμ2

(4)

式中iμ1和iμ2分别为等效变换后的铁心励磁电流。可得两铁心磁路的磁压降表达式为

Hs1ls+Hy1ly+Hc1lc=Ndciμ1

(5)

Hs2ls+Hy2ly+Hc2lc=Ndciμ2

(6)

由于在每个铁心中，交流边柱、轭铁和直流中柱的截面积不同，因此在流过相同磁通的情况下各部分的磁压降大小不同。简而言之，可以将等效励磁电流iμ1和iμ2分别分解为对应交流边柱、轭铁和直流中柱3个部分。

iμ1=iμ1.s+iμ1.y+iμ1.c

(7)

iμ2=iμ2.s+iμ2.y+iμ2.c

(8)

且满足如下条件

Hs1ls=Ndciμ1.s，Hy1ly=Ndciμ1.y，Hc1lc=Ndciμ1.c

(9)

Hs2ls=Ndciμ2.s，Hy2ly=Ndciμ2.y，Hc2lc=Ndciμ2.c

(10)

公式(7)、(8)表明，对每个铁心而言，其等效励磁电流都可以分解为3部分，并且这3部分可以分别表示3个拥有不同均匀截面积及磁路长度的独立闭合铁心的励磁电流。根据公式(9)、(10)，这3个等效独立闭合铁心的磁动势分别与交流边柱、轭铁和直流中柱的磁压降对应。并且等效后的励磁电流iμ1.s、iμ1.y、iμ1.c(或者iμ2.s、iμ2.y、iμ2.c)由3个独立铁心的非线性B-H曲线决定。

基于上述分析可知，超导限流器完整的等效电路图如图5所示。可以看出，图4所示的每个铁心及其绕组关系可以等效为3个均匀独立的闭合铁心并联。并且这3个铁心的中心线长度、铁心截面积分别与交流边柱、轭铁和直流中柱相一致。因此超导限流器的限流电感Lμ等于等效的3个铁心限流电感的并联值，即

(11)

式中：Lμ1、Lμ2分别为2个铁心的实际限流电感；Ls1、Ls2、Ly1、Ly2、Lc1、Lc2分别为图5中每个励磁支路的励磁电感。对于图5所示的每个闭合铁心的等效电感

图5 超导限流器铁心等效电路图Fig.5 Equivalent circuit diagram of iron-core of superconducting fault current limiter

值可以根据式(12)得出[15]

(12)

式中：N为铁心绕组匝数；A为铁心截面积；l为铁心中心线长度；μ为铁心磁导率。由于对于结构确定的超导限流器来说，N、A和l为已知常数，因此只要求出铁心相应的磁导率μ，就可以精确地估算出超导限流器的限流电感值Lμ。

2 超导限流器仿真实现

2.1 基于Simulink/Stateflow的超导限流器的模型实现

本文以两独立铁心结构的主动式饱和铁心型超导限流器为例，详细阐述等效磁路法在Simulink/Stateflow中的算法实现流程[16]。

磁通φ、磁感应强度B以及磁场强度矢量H的关系可由式(13)～(14)表示

φ=BA

(13)

B=μH

(14)

在忽略漏磁的情况下，如图4所示，磁路C1、C2流过的磁通分别为φC1、φC2。因此公式(1)、(2)可以转换为

(15)

(16)

式中：μs1、μy1、μc1、μs2、μy2、μc2分别为等效铁心Cs1、Cy1、Cc1、Cs2、Cy2、Cc2的磁导率。进一步转化得

(17)

(18)

也就是说，当求出流过2个铁心的磁通后，我们就可以根据公式(17)、(18)得出超导限流器的实际限流电感值。

根据上述分析，超导限流器可以根据下述步骤实现其电磁暂态仿真：(1)由于在仿真中，iac、idc、Nac、Ndc均为已知量，因此对于每个仿真节点来说，超导限流器2个铁心的磁动势F1、F2均可求出；(2)根据磁动势F1、F2及铁心的基本磁化曲线，通过解非线性方程(15)、(16)求得铁心磁通大小φC1、φC2以及每个等效铁心的磁导率μs1、μy1、μc1、μs2、μy2、μc2；(3)最后通过公式(12)求得超导限流器的限流电感Lμ。

在整个计算流程中，难度在于第2步。在给定磁动势大小的情况下，由于磁动势F与磁通φ是较复杂的非线性关系，难以用一般方法求解，这就需要用迭代算法来求取，进而得到等效限流电感。本文采用牛顿迭代法完成求解过程，牛顿法的核心是把非线性方程的求解过程，转变为反复求解对应的线性分量方程，并用线性分量方程的解不断修正非线性方程解的过程。

由于磁通φ为未知量，因此式(15)、(16)可以转化为

f(φ)=0

(18)

根据牛顿法，其修正方程可以表示为

f(φ(k))+f′(φ(k))Δφ(k)=0

(19)

式中：k为迭代次数，因此磁通φ的k+1步迭代解向量可以表示为

φ(k+1)=φ(k)+Δφ(k)=φ(k)-f(φ(k))/f′(φ(k))

(20)

当迭代算法满足收敛条件时，退出迭代，输出磁通φ在当前磁动势F下的解。

(21)

式中ε是设定的最大容许误差。

基于Simulink/Stateflow平台，实现了上述算法流程，最终实现了对超导限流器接入输电线路电磁暂态的分析。图6为Simulink/Stateflow中的算法实现流程图。

图6 基于Simulink/Stateflow超导限流器算法流程图Fig. 6 Algorithm process in Matlab/Stateflow

2.2 超导限流器电磁暂态仿真验证

超导限流器拟安装于500 kV超高压输电线路M至N站线路。超导限流器安装在M站变电站内，具体位置在M站至N站上M站侧线路出口处，其拓扑结构图如图7所示。

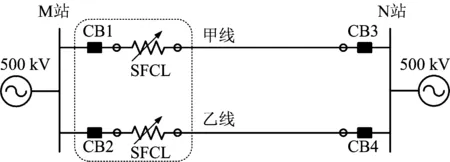
图7 超导限流器接入500 kV输电线路示意图Fig.7 Schematic plot of superconducting fault current limiter switching into 500 kV transmission line

应用上述等效磁路法及图6所示的非线性算法流程，对超导限流器在故障发生后的电磁暂态过程进行了详细分析。在仿真中，超导限流器各项结构参数如表1所示。

仿真设置在0.3 s时输电线路发生单相接地故障，此时超导限流器开始限流。图8为故障发生前后故障

表1 超导限流器主要结构参数

Table 1 Main structural parameters of superconducting fault current limiter

相的短路电流曲线。可以看出，在故障发生前，超导限流器的限流阻抗几乎可以忽略，这是由于此时流经交流绕组的电流比较小，不足以使铁心退饱和运行，铁心磁导率较低，呈现的阻抗较小。在发生故障后，故障相短路电流较未安装超导限流器时显著下降，这是因为短路后故障相短路电流足够大，使得故障相超导限流器铁心退出饱和区进入非饱和区，铁心磁导率急速增大，限流阻抗增大，超导限流器开始限流。

图9为故障发生前后故障相超导限流器电压变化曲线。可以看出，在故障发生前，超导限流器电压降几乎为0，也就是说其接入对线路基本无影响。在故障发生后，超导限流器的电压迅速增大，起到限流器作用。在1个周期内，当超导限流器铁心退出饱和区时，铁心磁导率迅速增大，使得超导限流器限流阻抗急剧增大，超导限流器电压降随之迅速增大；当超导限流器运行在饱和区时，铁心磁导率迅速下降，限流阻抗急剧下降，超导限流器电压降随之迅速减小。因此在1个周期内，超导限流器的电压波形呈现出尖顶波。

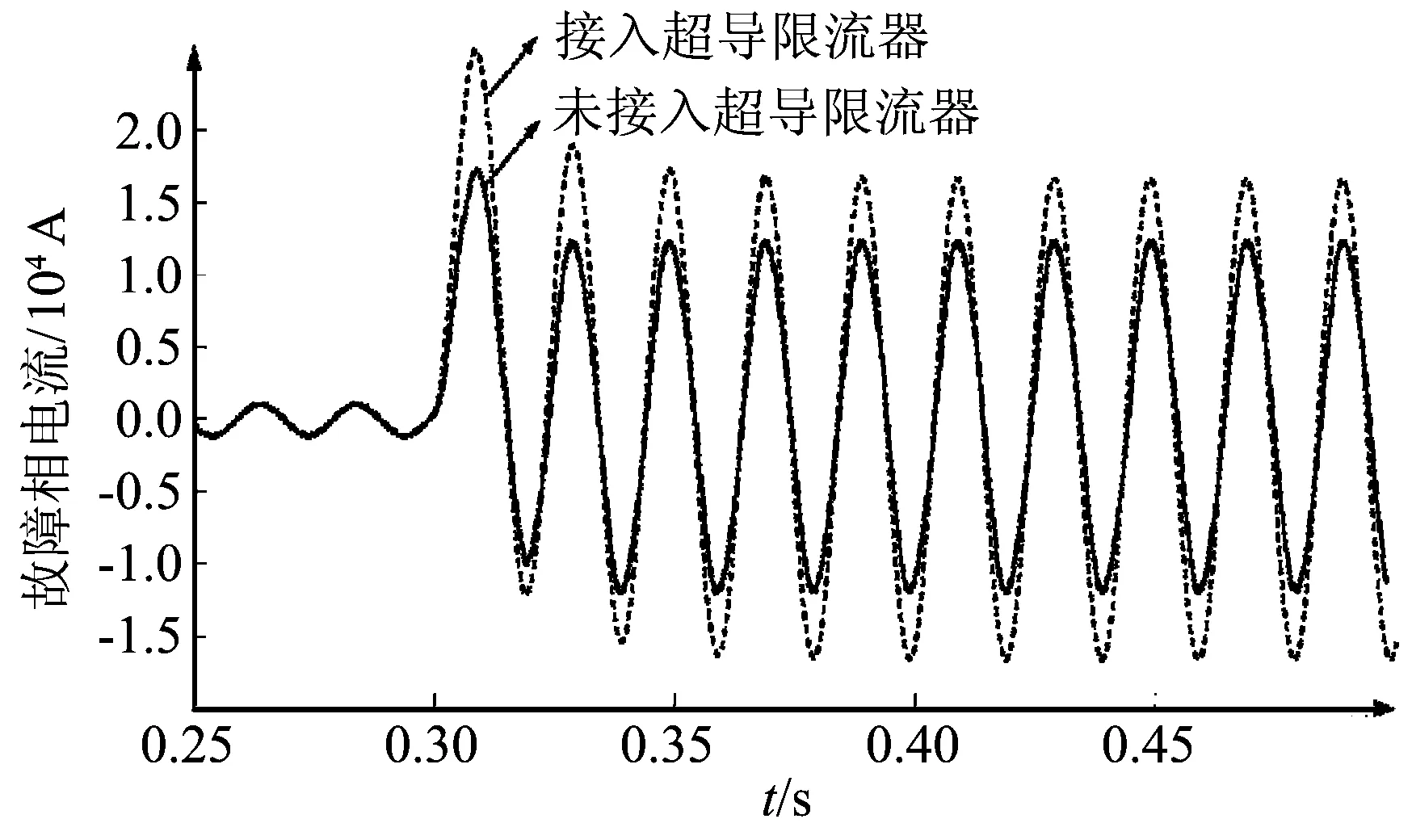
图8 超导限流器限流效果Fig.8 Current-limiting effect of superconducting fault current limiter

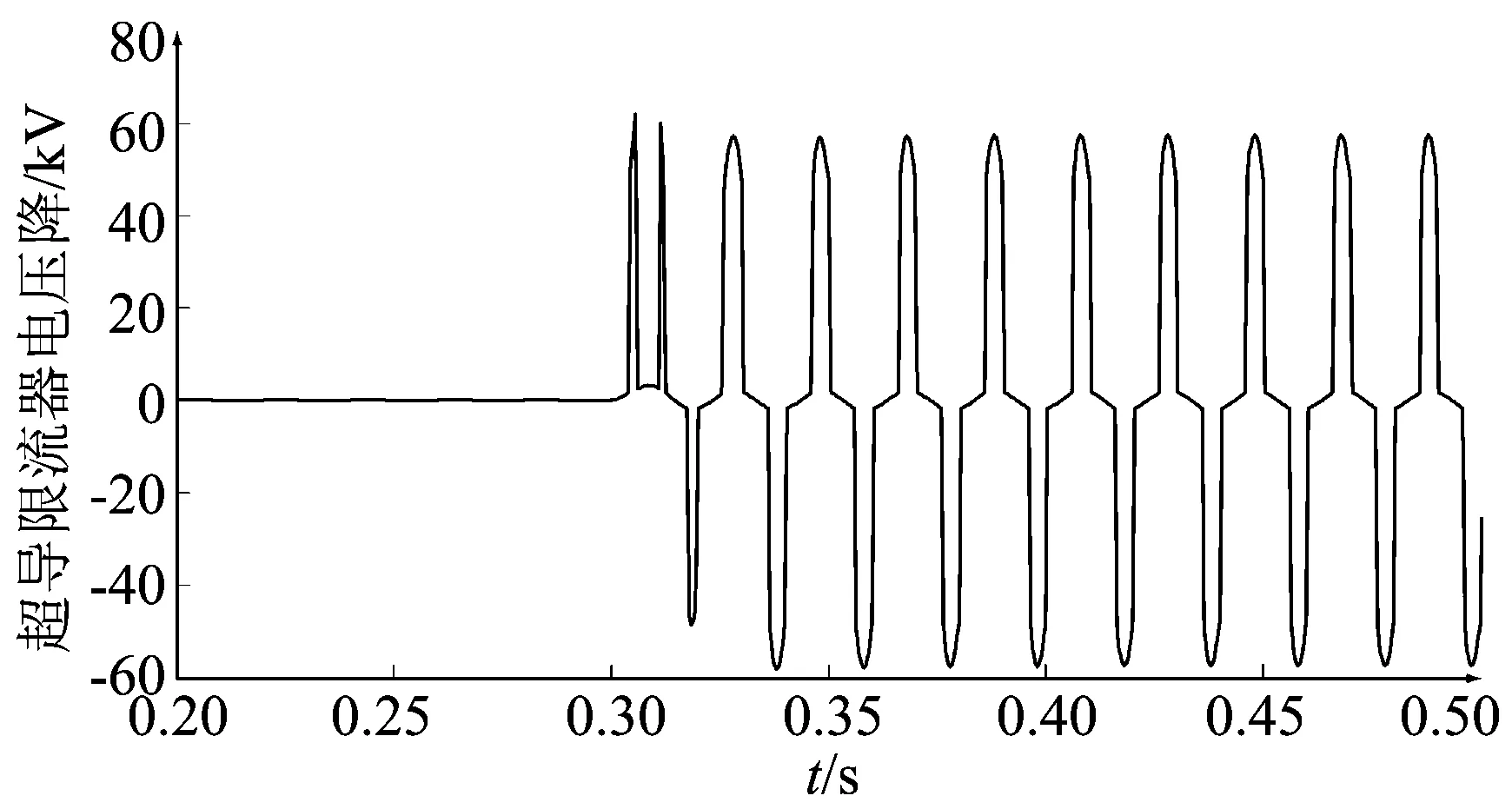
图9 超导限流器电压降Fig.9 Voltage drop across superconducting fault current limiter

图10和图11分别为故障发生前后超导限流器两铁心的磁动势及磁通变化曲线。铁心的磁动势及磁通在故障发生前分别为3.96×105 A和1.298 Wb。故障发生后铁心磁动势随着短路电流的变化而变化，而通过迭代算法，磁通曲线也可以得到。由图11可以看出，故障发生后，当短路电流足够大而使得铁心退出饱和区时，铁心的磁通急剧减小。

以上仿真结果与理论分析完全吻合，为分析超导限流器接入对电网的影响，其电磁暂态过程是分析的基础，因此等效磁路法的提出对超导限流器的实际应用有重大的意义。

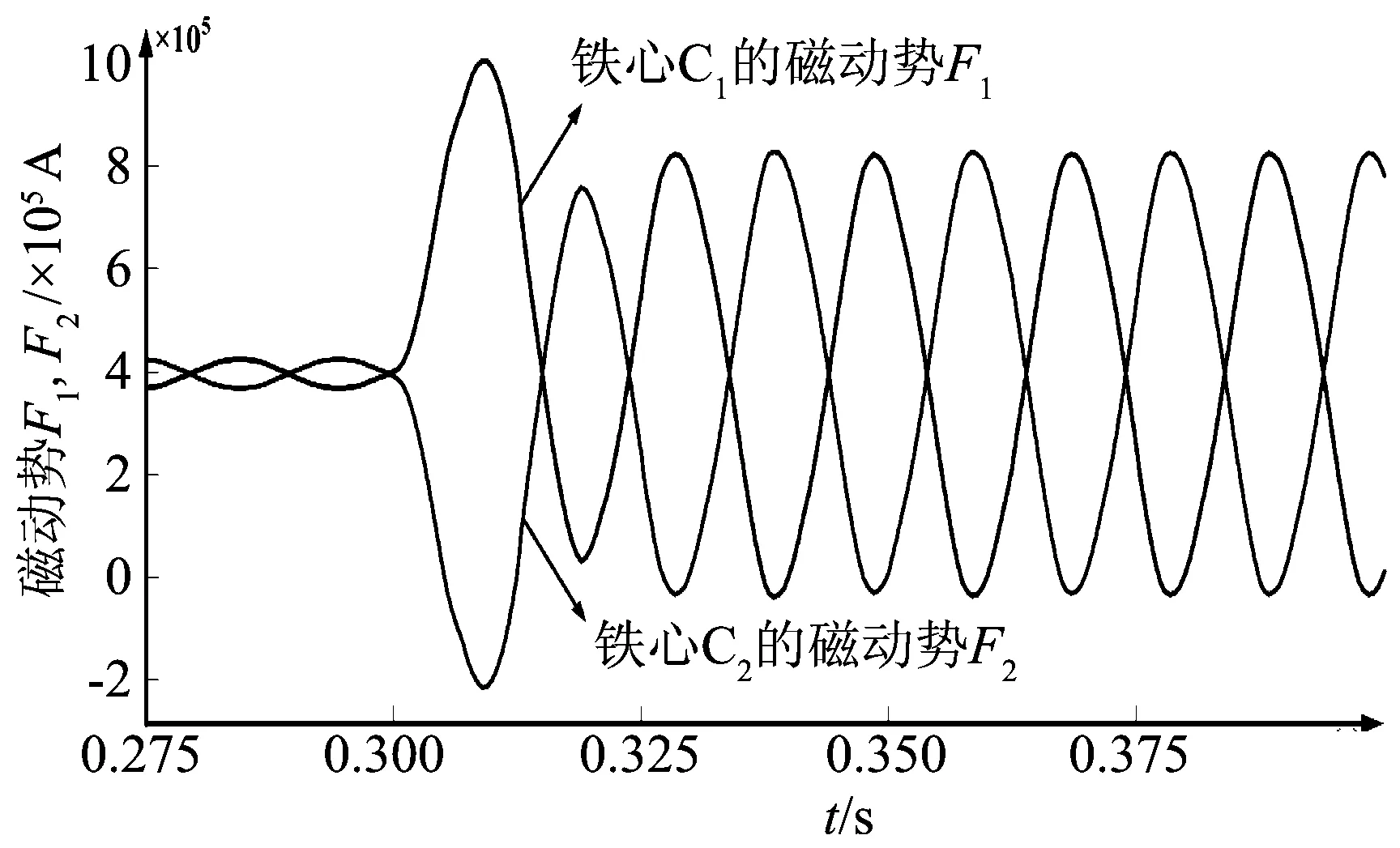
图10 超导限流器两铁心磁动势变化曲线Fig.10 Magnetomotive force change of two iron cores in superconducting fault current limiter

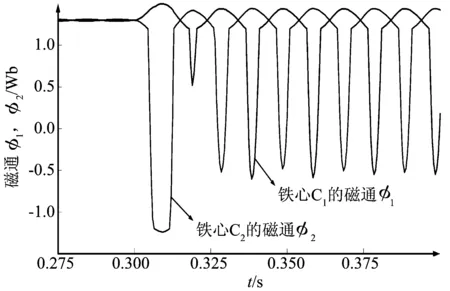
图11 超导限流器两铁心磁通变化曲线Fig.11 Magnetic flux change of two iron cores in superconducting fault current limiter

3 结 论

本文对饱和铁心型超导限流器的原理进行了详细分析，饱和铁心型超导限流器是一种基于铁心磁导率非线性特性变化而改变限流阻抗的非失超型超导限流器。针对超导限流器的非线性特性及其实际应用结构(采用铁心不等截面积设计)，本文提出了一种新式等效磁路法，有效、精确地分析了饱和铁心型超导限流器接入线路发生故障后的电磁暂态特性，并在Simulink/Stateflow仿真平台实现了饱和铁心型超导限流器的仿真实现，所得结果与理论结果完全吻合。新等效磁路法的提出对于饱和铁心型超导限流器的理论研究与实际应用都有重大意义。

[1]Leonard K， Xing Y， Kasegn T， et al. Applications of superconducting fault current limiters in electric power transmission systems [J]. IEEE Trans on Applied Superconductivity， 2005， 15(2)： 2130-2133. [2]金涛， 徐颖， 周世平， 等. 饱和铁芯型超导限流器研究进展综述[J]. 低温与超导， 2012， 41(1)： 13-18. Jin Tao, Xu Ying. Zhou Shiping, et al. Summarization of R&D on DC biased iron core type superconductive fault current limiter[J]. Cryo. & Supercond., 2012,41(1):13-18.

[3]Abbott S B， Robinson D A， Perera S， et al. Simulation of HTS saturable core-type FCLs for MV distribution systems [J]. IEEE Trans on Power Delivery， 2006， 21(2)： 1013-1018.

[4]Zhao C X， Wang S H， Qiu J， et al. Transient simulation and analysis for saturated core high temperature superconducting fault current limiter [J]. IEEE Trans on Magnetics， 2007， 43(4)：1813-1816.

[5]Rozenshtein V， Friedman A， Wolfus Y， et al. Saturated cores FCL-A new approach [J]. IEEE Trans on Applied Superconductivity， 2007， 17(4)： 1756-1759.

[6]Xin Y， Gong W Z， Niu X Y， et al. Development of saturated Iron core HTS fault current limiters [J]. IEEE Trans on Applied Superconductivity， 2007， 17(2)： 1760-1763.

[7]王付胜， 刘小宁. 饱和铁心型高温超导故障限流器数学模型的分析与参数设计[J]. 电气工程学报， 2003， 23(8)： 135-139.

[8]Li B， Li C， Guo F R， et al. Coordination of superconductive fault current limiters with zero-sequence current protection of transmission lines [J]. IEEE Trans on Applied Superconductivity， 2014，24(5)： 5602105.

[9]Philip A C， Jeffrey W M. Analytical nonlinear reluctance model of a single-phase saturated core fault current limiter[J]. IEEE Trans on Power Delivery， 2013， 28(1)： 450-457.

[10]Moriconi F， Koshnick N， Rosa F， et al. Modeling and test validation of a 15 kV 24 MVA superconducting fault current limiter. Proc [C]// IEEE Power Energy Soc Transm Distrib Conf Expo，2010:1-6.

[11]Li B, Li C, Guo F R, et al. Overcurrent Protection Corrdination in A Power Distribution Network with The Active Superconductive Fault Current Limiter[J]. IEEE Trans. on Applied Superconductivity, IEEE Trans. Applied Superconductivity, 2014, 24(5): 5602004.

[12]陆婷. 饱和铁心型高温超导限流器的设计与仿真[D]. 成都： 电子科技大学， 2008.

[13]Jaime C A， Jose L-R， Jacob C C et al. Magnetic flux analysis in superconducting fault current limiters under short-circuit conditions [C]. IEEE International Conference on Power System Technology (POWERCON)， 2012:1-5.

[14]Noe M， Steurer M. High-temperature fault current limiters： concepts， applications and development status [J]. Superconductor Science and Technology， 2007， 20(3)： 15-27.

[15]Raju B P， Parton K C， Bartram T C. A current limiting device using superconducting d.c. bias applications and prospects [J]. IEEE Trans on Power Appar & Syst， 1982， 101(5) ：3173-3177.

[16]Yang X， Kirby B， Zhao Q， et al. Model-based design process for product development of substation IEDS [C]. IEEE ENERGYCON Conference & Exhibition，2012: 968-974.

(编辑：刘文莹)

Electromagnetic Transient Analysis of Saturated Iron-Core Superconducting Fault Current Limiter

HE Jian1， GUO Fengrui2

(1.China Energy Engineering Group Guangdong Power Engineering Co., Ltd., Guangzhou 510663, China;2.State Grid Tianjin Electric Power Company, Tianjin 300072, China)

With the continuous expansion of power grids, the limit-exceeding problems of short-circuit current has become one of the prominent factors restricting the growth and development of power grid load. The traditional limiting measures have been difficult to meet the development of modern power system. Along with the rapid development of superconducting material, the fast and effective current limiting devices—superconducting fault current limiter has emerged as the times require. Due to the outstanding performance, the saturated iron-core superconducting fault current limiter (SICSFCL) has been applied in transmission lines and distribution systems. Considering the actual structure of SICSFCL, a new equivalent magnetic circuit method was proposed, which could accurately and effectively analyze the transient characteristics of the current limiter. The equivalent magnetic circuit method is important for the theoretical analysis on SICSFCL and its actual application.

saturated iron-core superconducting fault current limiter (SICSFCL); electromagnetic transient analysis; equivalent magnetic circuit method; Newton iteration

TM 72

A

1000-7229(2015)06-0070-07

10.3969/j.issn.1000-7229.2015.06.012

2014-12-25

2015-04-29

何健(1982)，男，硕士，主要从事电网输变电工程设计研究及项目管理等工作；

郭丰瑞(1989)，男，通信作者，硕士研究生，主要研究方向为电力系统保护与控制。