配电网中分布式储能系统一致性主动控制
2015-03-11吴鸣崔光鲁季宇刘海涛李洋于辉陈中
吴鸣,崔光鲁,季宇,刘海涛,李洋,于辉,陈中
(1.中国电力科学研究院,北京市100192;2. 东南大学电气工程学院,南京市 210096)
配电网中分布式储能系统一致性主动控制
吴鸣1,崔光鲁2,季宇1,刘海涛1,李洋1,于辉1,陈中2
(1.中国电力科学研究院,北京市100192;2. 东南大学电气工程学院,南京市 210096)
提出了一致性主动控制的方法对分布式储能装置进行优化控制,每一控制目标只需和邻近目标交互局部信息,在没有全局性信息的场景下实现全局最优一致性控制。一致性主动控制方法使系统中储能装置处于相同的放电比例状态,以满足实际应用的要求。该方法通过对一个Leader节点的监控,结合局部储能装置间主动的信息通信实现最终一致性的目标。基于IEEE3和IEEE32系统的算例结果验证了配电网分布式储能系统一致性主动控制算法的可行性和有效性。
分布式储能;一致性主动控制;局部信息通信;配电网
0 引 言
分布式电源,尤其是风力发电、太阳能光伏发电等可再生能源,直接布置在配电网或分布在负荷附近,对于能源集约利用具有重要意义。然而,风电、光伏发电等功率输出具有较大的随机性,而用户自备分布式电源一般是根据用户自身需要安排机组运行,因此分布式电源的大量接入增加了配电网调度与运行的复杂性,对配电网的规划、建设和运营都有着深刻的影响[1-6]。储能系统的应用可以有效改善功率分布,减小随机能源的影响,提高配电网的运行经济水平。
目前在配电网中通常会配置多个分布式小容量储能装置,相比单个大容量储能装置,更易于提高配电网运行的安全性和经济性,但对储能系统功率分配的协同控制提出了更高要求。针对配电网储能系统的优化控制,国内外已有一些研究[7-13]。文献[9]提出了一个独立的可再生能源发电系统模型,采用配套的电解剂和燃料电池组合来解决分布式电力系统中的峰值能量控制,并用电池进行能量缓冲。文献[10]建立了分布式发电系统和储能系统互补的数学模型,采用直接转矩控制算法对系统的能量互补过程进行控制。文献[11]根据分布式电源的类型以及与储能装置的不同组合方式,采用不同的控制策略分别进行了相应控制器的设计,实现了负荷功率变化时不同分布式电源间变化功率的共享,在微电网孤岛运行时能为孤网运行系统提供频率支撑。
储能系统功率分配主要有2种控制管理方式:集中式控制管理和分布式控制管理。集中式控制管理方法是通过一个中心控制器经过在线计算后向全网发布控制命令[14-16]。该方法需要收集全局信息和全局的命令交互,如果分布式储能数量较大,运行成本会大大增加,同时长距离的信息通信也会影响系统控制的时效性。分布式控制管理方法的优越性在于使用的信息都来自于局部各个节点的测量,由于缺少全局信息很难及时处理全局性问题,比如解决总功率越限等问题时,无法通过整体的调度来实现功率的最优分配,效率不高。近年来基于多代理系统的分布式协调控制方法得到了广泛的研究,其中一致性算法是一种基于网络的完全分布式控制协议,在控制领域取得了较大的研究成果[17-19]。
本文研究一致性主动控制算法在配电网储能系统运行控制中的应用。通过相邻储能装置间的信息交互,配合一致性控制的优化算法使系统中分布式储能装置响应功率和容量的比例保持一致,以实现系统整体最优的目标。该方法并不要求全局信息进行通信,只需要局部信息的通信便可达到全局的最优化。同时,该方法还具有强鲁棒性的特点,在某些局部信息交互发生故障而无法通信时,该方法仍然可以通过有效局部信息交互完成全局的最优化。文章首先对一致性问题进行简单描述,然后分析功率约束条件和一致性主动控制方法,最后形成系统控制算法,建立一致性控制的模型,结合潮流计算形成控制算法,并通过在IEEE3和IEEE32系统中仿真,验证该控制算法的可行性和有效性。
1 控制策略
1.1 问题描述
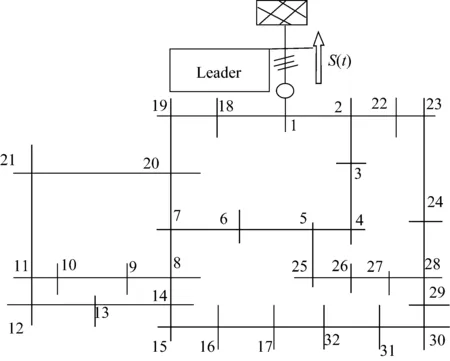
如图1所示,在带有分布式电源及储能装置的配电网中,考虑每一个负荷节点附近都装设的分布式电源和储能装置的协调控制问题。
以分布式光伏发电为例,在阳光照射条件很好的白天,光伏发电量比较大,而此时当地负荷相对较小,过剩功率从配电网流向外部系统,在连接节点上就有可能出现正向功率超过允许值的情况;相反在晚上,光伏发电较少,而当地负荷相对较大,外电网向配电网输送的功率也有可能出现超过反向允许值的情况。本文提出的一致性控制方法通过优化分配储能装置功率,不仅解决功率越限的问题,还根据电网稳定性要求设置了一个合理安全的运行点并使之运行在该点附近,确保配网安全运行。
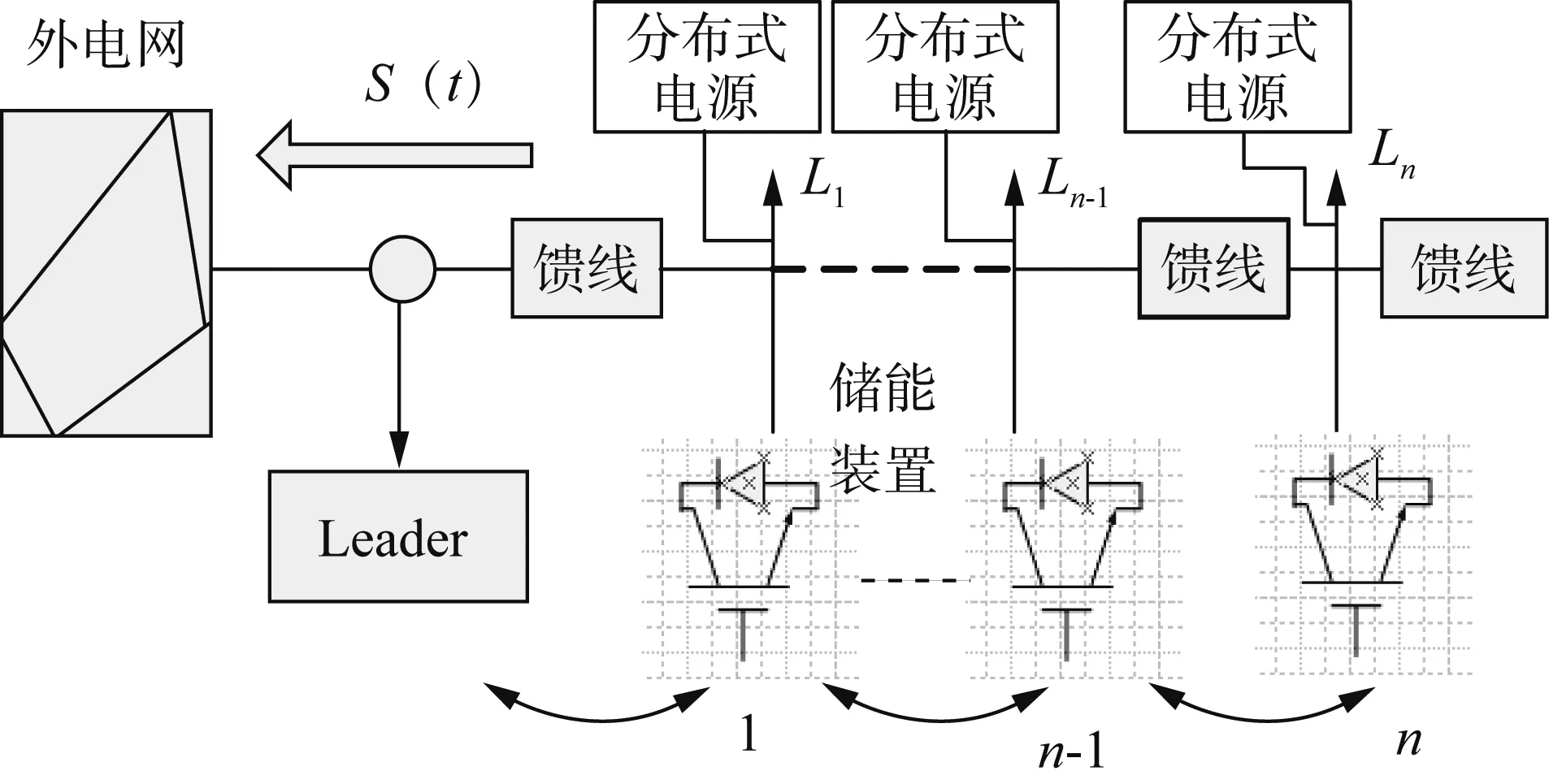
图1 带有分布式储能装置的配电网控制框图Fig.1 Control diagram of distribution network incorporating distributed storages
针对数量较大的分布式储能装置,如果是系统统一控制,对中心服务器以及信息通信系统的要求很高。本文采用局部联系的方法,通过相邻节点进行信息的通信,结合一致性控制算法达到全局一致的要求。本文的能量控制以储能装置输出功率保持比例一致为目标,这样使得储能装置可以根据自身容量条件合理安排出力大小。
1.2 功率约束描述
本文建立的控制模型中,在于外电网连接的馈线处设有控制装置Leader(如图1中所示),通过对流过Leader的功率进行监测来对一致性控制进行初始化,系统中所有的储能装置的控制都会与Leader保持一致,控制策略如图2所示。
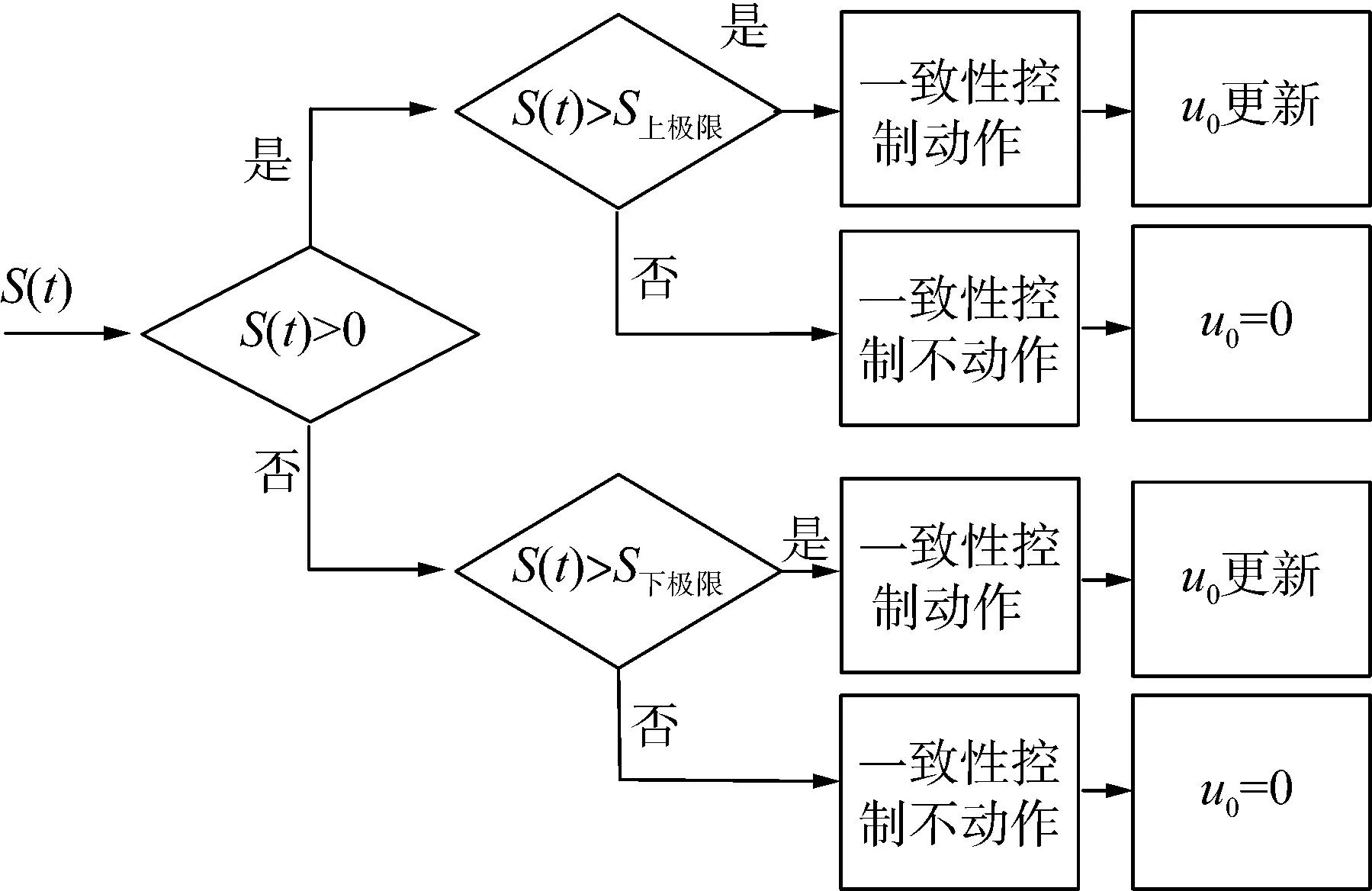
图2 Leader的控制策略Fig.2 Control strategy of Leader
如果Leader监测到功率由配电网流向外电网,那么S(t)为正,否则为负,利用S(t)作为电网负荷的控制变量。同时还定义了4个功率限制值:S下极限、S下合理、S上合理、S上极限(其中前2个为负值,后2个为正值)。在用电高峰期,如果S(t)比S下极限大,那么系统处于正常状态,一致性控制装置不动作;一旦S(t)比S下极限小,那么Leader会按照设置的算法主动启动一致性控制装置,直到S(t)比S下合理大,系统会保持前一刻状态运行。在用电低谷配电网功率过剩时的控制策略与前者类似。
本文中的功率约束就是将节点流过的功率控制在一定范围内,控制目标如下:
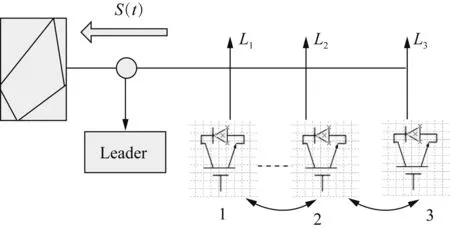
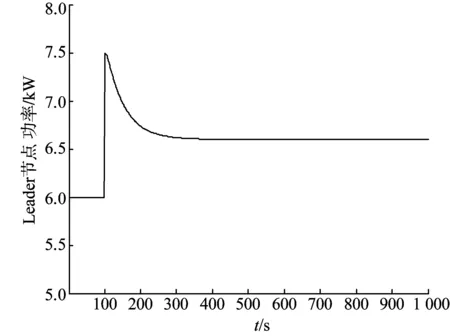
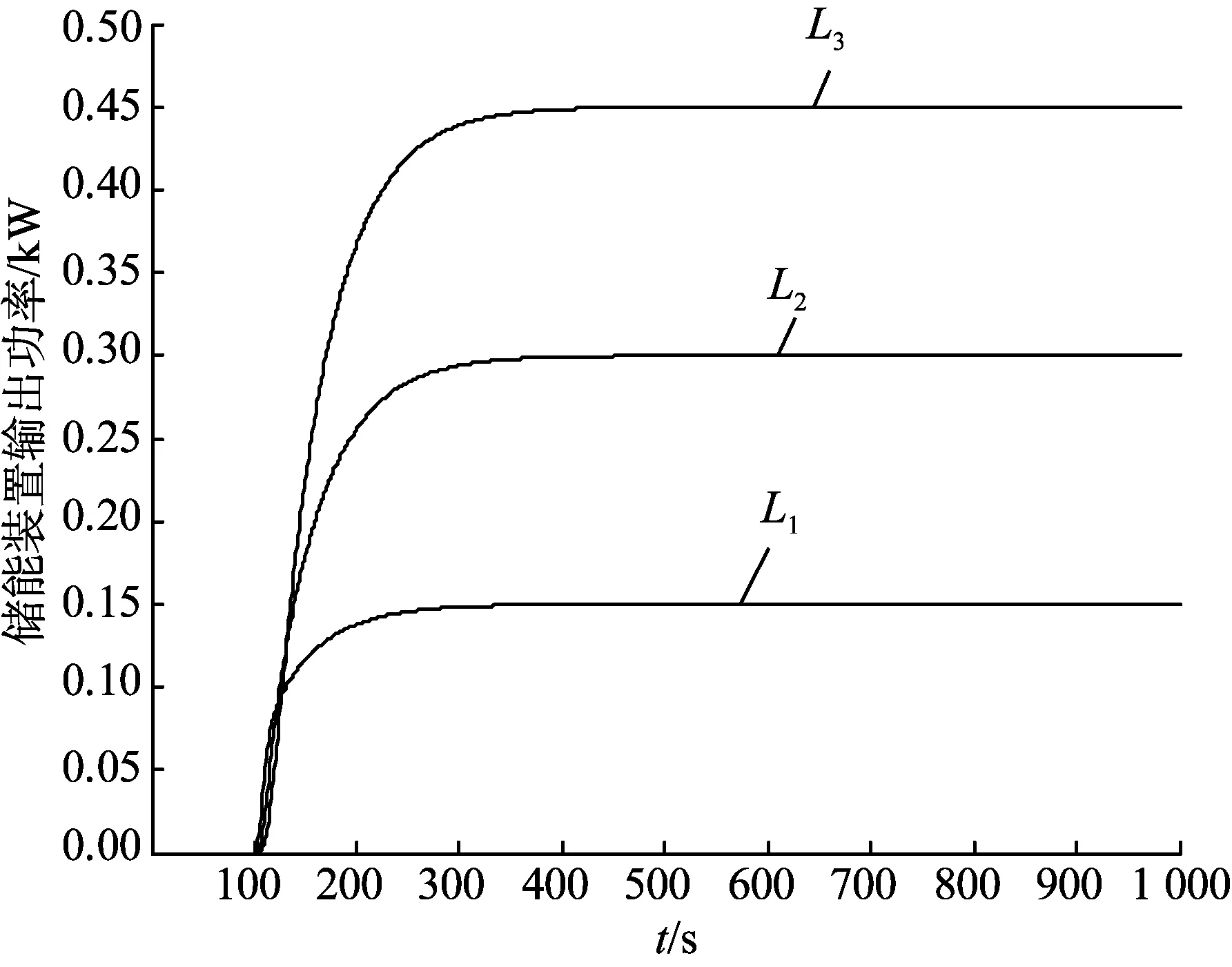
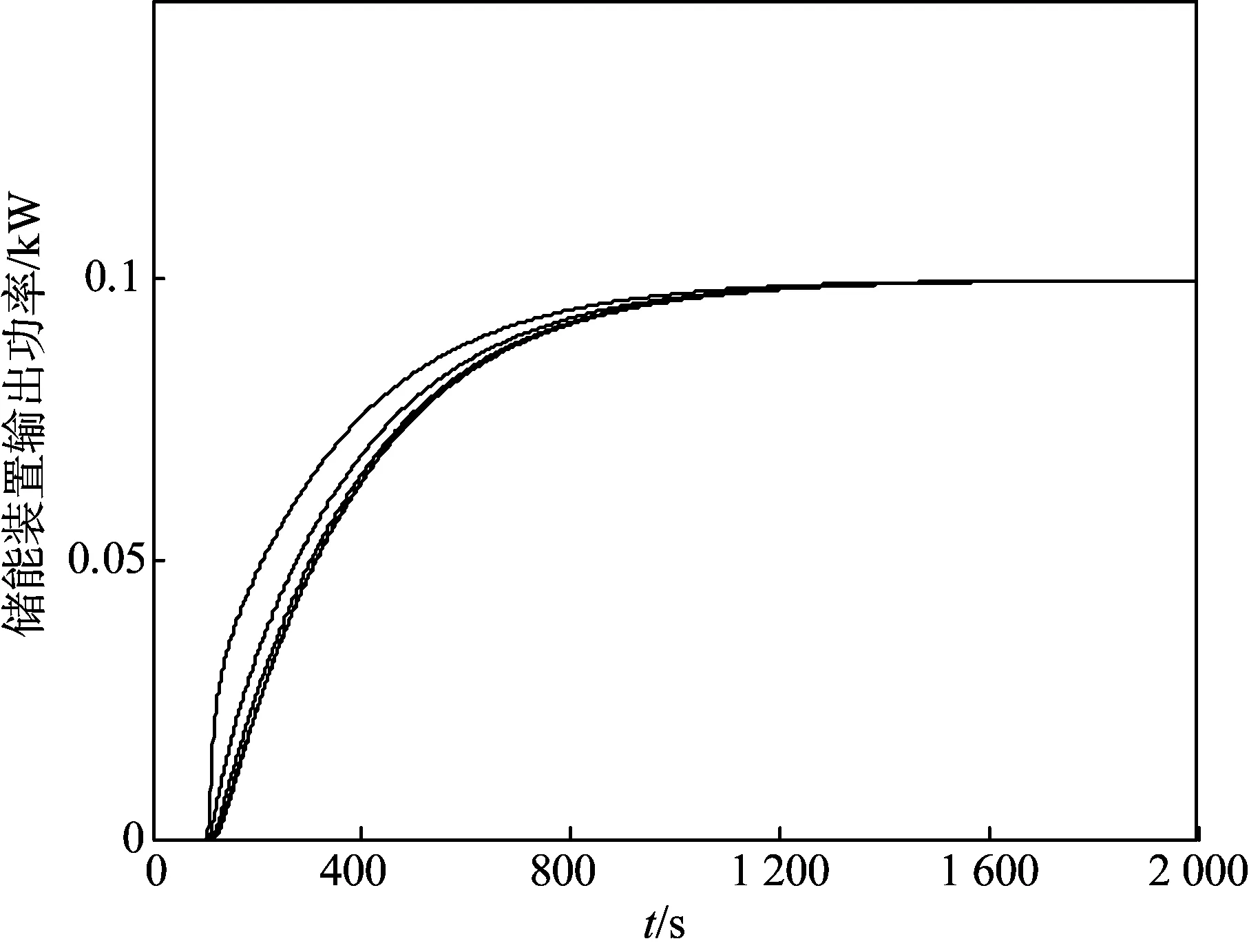
S下极限 (1) 当功率不满足限定条件时,各个储能装置会在Leader的协调下作出相应的功率输出调整。 1.3 一致性主动控制策略 在本文的一致性控制策略中,为了实现大规模的储能装置功率输出更加科学合理,控制所有的储能装置处于相同的放电状态,即所有储能装置都有共同的放电比例,即 (2) 式中:Pi表示第i个储能装置的输出功率;Pmaxi表示第i个储能装置能提供的最大功率。 对于大规模的储能系统,一致性控制的控制策略会比前文提到的2种控制方法更为有效,因为该方法仅需要局部的网络信息交互,而且综合了前2种方法的优点,避免了其不足之处。 储能系统中,各个储能装置的控制状态信息可以表示为 (3) 式中:ui(t)表示第i个节点在t时刻储能装置的控制信息;u0(t)表示Leader节点在t时刻的控制信息;cij表示第i个储能装置和第j个储能装置之间的通信联系,如果第i个储能装置和第j个储能装置之间可以通信,那么cij=1,否则cij=0,。此外,如果第i个储能装置可以与Leader通信,那么ci0=1,否则ci0=0,cii=1适合于任意一个储能装置,表示所有的储能装置都能从自己得到信息。 (4) 式(4)所表示的矩阵为一个稀疏矩阵,由于本文采用的是局部的一致性控制,必然会有一些点之间没有联系,这些点之间的通信系数都是0,矩阵也就是一个稀疏矩阵。同时,必须注意的是,该矩阵还是一个时变的矩阵,因为2个储能装置之间的联系并不是不变的,由于某种原因在某些时刻,2个储能装置之间的通信会发生中断等故障,考虑时变的通信系数矩阵有利于在故障状态下对储能系统进行分析。 为了实现系统的一致性控制,根据一致性控制理论[19-20],选择控制策略如下: 在储能系统中,第i个储能装置的端电压表示为Ui,输出电流表示为Ii,输出有功功率可以表示为 Pi=UiIi (5) 则 (6) 在配电网中,考虑到无功充足的情况下,节点电压Ui一般保持额定值,公式(6)可化简为 (7) 如果 (8) 则,要实现公式(3)中的一致性,只需要ui(i=1,2,…,n)达到一致即可。式(8)可表示为 (9) 式(14)满足多智能体一般动态方程,储能装置的一致性算法可描述为 总之,德育是一切教育的前提,我们应不断改革和完善德育工作模式,让德育教育更加贴近学生的生活,让学生真正成长为德才兼备的有用之材。 ci0[u0(t-td)-ui(t-td)]} (10) 式中ki>0为储能装置的控制增益。 (11) 那么,第i个储能装置的控制信息为 (12) 对于Leader节点的控制信息,可由图2的Leader控制策略知,当S(t) (13) 式中kp为控制调节系数,用来调节到达一致状态速度。 当S(t)>S上极限时,有 (14) 可得: (15) (16) 因此,每个储能装置在一个时间段内需要输出的功率可以表示为 Pi(t)=ui(t)×Pmaxi (17) 式中Pi(t)表示第i个储能装置在t时间段内输出的功率。值得注意的是,公式中未考虑储能装置内部的动态特性,因为本文只关心储能装置的功率输出,而且储能装置内部的动态特性要比功率输出的变化慢得多,所以式(17)具有一定的可行性。 在储能装置调整结束之后,需要对配电网进行一次潮流计算,更新配电网状态。 (18) 式中:Pj(j=1,2,…,n)表示各个节的点注入功率;x为控制变量;y为状态变量。 控制算法中,Leader节点的控制信息是通过监测Leader节点实时潮流状态,结合系统限定功率情况,经过式(13)~(16)计算而来;各个储能装置的控制信息是由前一状态的控制信息,结合相邻储能装置通信的信息,经过公式(10)~(12)计算而来。由控制器发出控制信息,经过电力电子装置根据控制要求控制输出功率,以满足配电网潮流的平衡和功率不越限的条件。 完整的控制算法可以由公式(12)~(18)表示。其中,公式(12)~(14)表示控制功率不越限的条件,主要的控制对象是Leader,当S(t)>S上极限时,一致性控制便会启动,Leader将会被初始化,控制信息u0会被更新;由公式(15)~(16)可知ui也会随着u0而改变,各个储能装置会相应的减少功率输出,直到S(t)降到S上合理各个储能装置才会停止减少输出功率,并维持该状态直到负荷变化。在Leader检测到负荷并未越限的情况下,如果配电网当前实际负荷S(t) 公式(18)表示配电网的潮流计算,在进入当前时间段之前,系统都会进行一次潮流计算,潮流计算的原始数据主要来自上个时间段功率输出调整之后的储能装置节点信息,当前的潮流计算会被用作此次Leader节点是否动作的判断依据。 系统的完整流程图如图3所示。 3.1 算例1 为了验证配电网一致性主动控制算法的可行性,采用了典型的配电网络。配电网包含3个等效负荷节点,在每个等效负荷节点处都装设有分布式电源、 图3 控制系统算法完整流程图Fig.3 Flow chart of control algorithm 负荷和储能装置,具体的通信联系如图4所示。负荷节点的负荷信息如表1所示,储能装置所能提供的功率如表2所示,功率限定情况如表3所示。等效负荷在100 s时突然增加25%负荷,仿真结果如图5、6所示。 图4 算例1 配电网示意图Fig.4 Distribution network in Example 1表1 节点的负荷信息Table 1 Bus load information 表2 储能装置最大功率Table 2 Maximum power of energy storage devices 表3 功率限定值Table 3 Power limit kW 图5 功率限制条件Fig.5 Power constraints 图6 储能装置功率输出Fig.6 Output power of energy storage devices 由图5可知,在t=0到t=100 s之间,配电网的负荷在允许的范围之内,因此,所有的储能装置都没有发生动作。当t=101 s时负荷突然增加了25%,这使得配电网负荷超过了S上极限,所以此时Leader节点控制信息被更新,一致性控制开始动作。经过一段时间的调整,配电网负荷逐渐降低至S上极限以下;本算法的控制目标是降低到合理运行点,所以一致性控制会继续调整,一段时间后,功率调整目标向S上合理靠近,当达到S上合理时,控制信息保持前一状态不变,控制到达稳定状态。此时已经满足了功率限定的条件。此外,由图6可知,P1/Pmax1=0.15/0.5=0.3,P2/Pmax2=0.30/1=0.3,P3/Pmax3=0.45/1.5=0.3此时,三者相等,满足一致性控制的要求。 3.2 算例2 在算例2中,本文采用了IEEE32节点的网状配电网来验证文中一致性主动控制算法在不同配电网中的有效性。这是一个12.66 kV的环形网络,具体情况可见文献[21]。配电网络如图7所示,每个节点都接入分布式电源和当地负荷,并安装储能装置。为了模拟的简化,假设每个负荷节点的等效负荷都相同,均为100 kW,在100 s时,由于分布式电源和负荷的波动,等效负荷增加了25%;同时,设定每个储能装置最大能提供的功率也相同,为50 kW。功率限定如表4所示,仿真结果如图8、9所示。 图7 算例2配电网环形网络Fig.7 Loop distribution network in Example 2表4 功率限定值Table 4 Power limit kW 由图8可知,在t=0到t=100 s之间,配电网的负荷在允许的范围之内,因此,所有的储能装置都没有发生动作。在101 s时,配电网负荷突然向上波动,超出了功率限制的范围,此时,Leader节点监测到功率越限,一致性控制便主动开始动作。经过一段时间的调整,功率逐渐降到允许范围内、但由于控制目标是运行合理点,一致性控制会继续调整,直到降低到S上合理以下。图9分别是5,10,15,20,25,30号节点储能装置的有功出力。在t=0到t=100 s之间,储能装置没有动作,储能输出均为0,在101 s时,配电网负荷超出功率限制的范围,储能会根据自身的调节能力调整出力最终达到出力一致。 图8 功率限制条件Fig.8 Power constraints 图9 储能装置功率输出Fig.9 Output power of energy storage devices 本文提出了储能系统一致性主动控制的方法,在功率约束的条件下,对系统一致性控制进行研究。通过控制原理中的一致性算法,将储能系统中各个储能装置的输出功率控制在同一比例;相比于传统方法,该算法的优越性在于只需要局部信息的通信便可达到全局的最优化,提高了控制效率,降低了控制成本。算例的结果表明,该算法能够实现配电网中储能系统的一致性主动控制。 [1]蒋心泽,董晓文,包海龙.分布式电源接人对配电网的影响[J].电力与能源,2011,01(1):83-86. Jiang Xinze,Dong Xiaowen,Bao Hailong.Research on theImpactof distributed generation sources on distribution networks[J].Power and Energy, 2011,1(1):83-86. [2]许素强.分布式电源接入对配电网的影响[J].中国科技纵横,2013(5):222. [3]刘锐,刘敏,辜俊明.浅析分布式电源接入对配电网的影响[J]. 机械工程与自动化,2013(3):220-222. Liu Rui, Liu Min, Gu Junming. Impact of distributed generation on distribution network[J]. Mechanicai Engineering Automation, 2013(3):220-222. [4]袁王峥,梁伟,陈思佳,等.分布式电源接入城市配电网规则分析[J].中国电力,2013,46(7):43-46. Wang Zheng, Liang Wei, Chen Sijia, et al.Rules of distributed generator integration to urban distribution network[J].Electric Power,2013,46(7):43-46. [5]袁沔齐,邹振宇,孙凯祺,等.基于遗传算法和微分进化算法的分布式电源优化配置[J].中国电力,2013,46(1):16-20. Yuan Mianqi, Zou Zhenyu, Sun Kaiqi, et al.Optimal allocation of distributed generation based on genetic algorithms and differential evolution algorithm[J].Electric Power,2013,46(1):16-20. [6]李泓泽,王宝,郭森.分布式电源接入配电网的经济效益及电压稳定性[J].中国电力,2012,45(3):33-37. Li Hongze, Wang Bao, Guo Sen. Economic benefits and voltage stability of distributed generation integrated into distribution network[J].Electric Power,2012,45(3):33-37. [7]田军.分布式发电系统储能优化配置[D].北京:华北电力大学,2011. Tian Jun. Optimal configuration of energy storage in distributed generation system[D]. Beijing: North China Electric Power University, 2011. [8]陈益哲.微网中分布式储能系统的建模与控制研究[D].武汉:华中科技大学,2011. Chen Yizhe. Studies on modeling and control of distributed energy storage system in microgrid[J]. Wuhan: Huazhong University of Science and Technology, 2011. [9]Bilodeau A,Agbossou K.Control analysis of renewable energy system with hydrogen storage for residential applications[J].Journalof Power Sources,2006,162(2),:757-764. [10]王健,康龙云,曹秉刚.可再生能源分布式发电系统能量互补控制的研究 [J].西安交通大学学报,2005,39(7):766-770. Wang Jian, Kang Longyun, Cao Binggang. Energy complementary control of a distributed renewable energy power generation system[J]. Journal of Xi’an Jiaotong University, 2005, 29(7):766-770. [11]王成山,肖朝霞,王守相.微网综合控制与分析[J].电力系统自动化,2008,32(7):98-103. Wang Chengshan, Xiao Zhaoxia, Wang Shouxiang. Synthetical control and analysis of microgrid[J]. Automation of Electric Power System, 2008, 32(7):98-103. [12]高文杰,井天军,杨明皓,等.微电网储能系统控制及其经济调度方法[J].中国电力,2013,46(1):11-15. Gao Wenjie, Jing Tianjun, Yang Minghao, et al.Operation control and economic dispatch of energy storage system for micro-grid[J].Electric Power,2013,46(1):11-15. [13]靳文涛,李建林.电池储能系统用于风电功率部分“削峰填谷”控制及容量配置[J].中国电力,2013,46(8):16-21. Jin Wentao, Li Jianlin. BESS for wind power “peak shaving” control and capacity configuration[J].Electric Power,2013,46(8):16-21. [14]Gan D, Thomas R, Zimmerman R. Stability-constrained optimalpower flow[J]. IEEE Transaction on Power System, 2000, 15(2):535-540. [15]Dent C, Ochoa L, Harrison G, et al. Efficient secure AC OPFfor network generation capacity assessment, IEEE Transaction on Power System, 2010, 25(1):575-583. [16]Saber R O,Murray R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transaction on Automatic Control,2004,49(9):1520-1533. [17]Fax J A,Murray R M.Information flow and cooperative control of vehicle formations[J].IEEE Transaction on Automatic Control,2004,49(9):1465-1476. [18]Saber R O. Flocking for multi-agent dynamic systems: Algorithms and theory[J].IEEE Transactionon Automatic Control,2006,51(3):401-420. [19]Xin H, Gan D, Huang Z, et al. Applications of stability-constrained optimal power flow in the East China system[J]. IEEE Transaction on Power System, 2010, 25(3):1423-1433. [20]Xin H, Qu Z, Seuss J, et al.A self-organizingstrategy for power flow control of photovoltaic generators in adistribution network[J]. IEEE Transaction on Power System, 2011, 26(3):1462-1473. [21]Kundur P. Power system stability and control[M]. New York: McGraw-hill, 1994. (编辑:张小飞) Consistent and Active Control for Distributed Energy Storage System in Distribution Network WU Ming1,CUI Guanglu2, JI Yu1, LIU Haitao1, LI Yang1, YU Hui1, CHEN Zhong2 (1. China Electric Power Research Institute, 100192, Beijing, China;2. School of Electrical Engineering, Southeast University, Nanjing 210096, China) The consistent and active control strategy was proposed for optimally controlling the distributed energy storage devices. Each control objectives only needed to interact with the neighboring target, and it could achieve the goal of global optimal consistency control without global information. The consistent and active control strategy could make the system energy storage device in the same proportion of discharge state to meet the requirements of practical application, which was based on the monitoring of the Leader node and combined with the interaction between local energy storage devices. The efficiency and feasibility of the consistent and active control algorithm for distributed energy storage system in distribution network were demonstrated by the example results of IEEE3 and IEEE32 bus systems. distributed energy storage; consistent and active control; communication of local information; distribution network 国家电网科技项目(多能互补小型化分布式电源应用模式与并网关键技术)。 TM 76 A 1000-7229(2015)06-0020-07 10.3969/j.issn.1000-7229.2015.06.004 2015-04-20 2015-05-10 吴鸣(1981),男,博士,高级工程师,主要从事分布式发电与微电网,主动配电网等方面的研究; 崔光鲁(1989),男,硕士,主要研究方向为电力系统配电网规划,继电保护测试; 季宇(1982),男,主要研究分布式电源、微电网运行控制与保护技术; 刘海涛(1978),男,主要研究方向为分布式电源、微电网的规划、控制技术,配网信息化技术; 李洋(1982),男,主要研究方向为分布式电源、微电网运行控制与能量管理技术; 于辉(1982),男,主要研究方向为分布式电源、微电网运行控制与能量管理技术; 陈中(1975),男,研究员,主要研究方向为电力系统稳定与控制,新能源的开发和应用。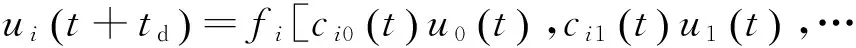
2 系统控制流程
3 算例分析






4 结 论
