解非线性优化问题GM(1,1)模型的多子群遗传算法

刘兵兵，郝庆一

(安庆师范学院 数学与计算科学学院，安徽 安庆 246133)



解非线性优化问题GM(1,1)模型的多子群遗传算法

刘兵兵，郝庆一

(安庆师范学院 数学与计算科学学院，安徽 安庆 246133)

摘要：针对非线性优化问题约束条件中待定参数的时间序列数据，首先使用GM(1,1)方法进行建模预测得到参数的预测值，进而将参数预测值代入原问题中提出一个确定型的非线性优化问题。对该确定型问题设计了一个多子种群并行进化的遗传算法进行求解，在分析所提算法的收敛性的基础上，给出了初步的数值算例。数值算例实验结果表明：该算法能够较为精确地获得预测型非线性优化问题的(近似)全局最优解。

关键词：GM(1,1)模型；非线性优化问题；均值白化；多子群遗传算法；全局最优解

灰色非线性优化问题从上世纪八十年代提出以后，在实际应用中取得了初步成效[1-6]。灰色非线性优化问题可以看作是普通非线性优化问题的拓展，但又与普通非线性优化问题有着明显不同的特点：灰色非线性优化问题在处理实际问题中的贫信息不确定小样本的参数数据特别有效。关于灰色非线性优化问题的研究可见[7-13]，文[10]考虑灰色线性和非线性优化问题的约束条件中的约束值的可变性，并给出一个预测型灰色线性模型的算例，通过GM(1,1)对使用时间序列描述的约束值进行建模预测，得到了约束参数变化趋势的时间序列函数模型。然后将预测值代入线性优化问题中再进行优化。文[10]虽然提出了预测型的灰色非线性优化问题，但是将约束值的预测结果带入原问题中得到的普通非线性优化问题在实践中大多呈现非凸非可微性，因此使用传统的求解方法将不再可行，即使转化以后的普通非线性优化问题具有可微与凸性，对于规模很大的问题，使用传统的优化方法难以保证实时性。因此本文首先考虑使用GM(1,1)建模方法来预测得到预测模型的白化问题，进而设计了一个多子种群并行进化的遗传算法进行求解，最后给出了初步的数值算例。

1灰色非线性优化问题的数学模型

普通的非线性优化模型中所有参数都视为固定不变的，事实上，实际问题的非线性优化问题中参数都在或大或小的范围内呈现一些波动性，灰色非线性优化问题就应运而生了。对于灰色非线性优化问题求解方法可见文[7-9]等。如果灰色非线性优化问题约束条件中的右端参数是由时间序列描述的，则不仅可以求解当前问题的最优解，而且可以通过灰色预测方法来预测这些参数在将来某特定时间节点的预测值，将这些参数的预测值带入灰色非线性优化问题中，就可以预测实际问题在将来特定时间节点的目标值，这在实践中有着非常重要的意义，可以给决策者提供较为可靠的信息以帮助决策者采取更合适的行动策略。下面给出非线性优化问题的灰色预测模型：

定义1设x=(x1,x2,…xn)T为决策变量，⊗(1)，⊗(i)(i=1,2,…,m),⊗(j)(j=1,2,…,l)均为灰参数集，并设r1=(r11,…,ri1,…,rm1)T与r2=(r12,…,rj2,…,rl2)T为约束右端参数向量，均由时间序列来描述，则称

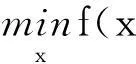
为预测型灰色非线性优化问题，记为PGCNLOP(Predicted-typeGrayConstrainedNonlinearOptimizationProblem)。其中f(x,⊗(1))为灰色目标泛函，gi(x,⊗(i))(i=1,2,…,m)与hj(x,⊗(j))(j=1,2,…,l)为灰色约束泛函。

如果上述PGCNLOP问题中的约束右端参数向量固定不变，则可以使用灰色优化问题的均值白化技术将PGCNLOP转化为一个普通的非线性优化问题，定义如下。

定义2对PGCNLOP中的灰色参数进行白化，可得如下的普通非线性约束优化问题

称该问题为PGCNLOP的白化问题。

如果对PGCNLOP中的约束右端参数的时间序列进行GM(1,1)建模，预测得到在未来特定时间节点的参数值，分别记为ri1(t)和rj2(t)。将ri1(t)和rj2(t)代入定义2中的白化问题，则可以得到如下的预测型白化问题。

定义3称下面的非线性约束优化问题

为问题PGCNLOP的预测型白化问题。

2约束参数向量的GM(1,1)建模

考虑问题PGCNLOP约束中的右端参数向量设r1=(r11,…,ri1,…,rm1)T与r2=(r12,…,rj2,…,rl2)T，设分量ri1(i=1,…,m)和rj2(j=1,…,l)均由时间序列来刻画，可采用GM(1,1)建模方法来得到它们的预测函数模型，具体建模步骤如下(以参数ri1为例)：

(2)ρ(s)∈[0,ε],s=2,3,…,m;

(3)ε<0.5，

第六步：确定序列预测模型的白化方程及时间响应式分别为

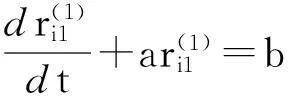
第八步：检验误差。算出残差平方和进而得到平均相对误差。若满足精度要求，则建模结束；否则可对残差序列建立GM(1,1)模型，对原来的模型进行修正。

3多子群遗传算法与数值算例

3.1多子群并行进化遗传算法

对于定义3中给出的预测型均值白化问题，使用上节中的GM(1,1)建模得到预测型均值白化问题的约束右端参数向量在时刻点T(T>k)预测值并代入该模型中，便可得到下面的确定型约束非线性优化问题，记为DNLOP(T)

由于在实践建模中得到的约束非线性优化问题大多都是非凸非光滑的，甚至连续性都难以保证，因此使用传统的基于导数的优化方法基本不再可行。即使问题满足凸性和光滑性，当问题的数据规模很大时，传统的求解方法也难以保证实时性。基于此，我们设计了一个多子种群并行进化的遗传算法来求解该问题。

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，它是一种通过模拟自然进化过程搜索最优解的方法，由密西根大学Holland教授在1975年首先提出来。基本遗传算法的步骤主要包括：生成初始种群、通过适应度函数进行选择、对种群中的个体进行交叉与变异操作以得到下一代种群。为了保证能够找到问题的最优解，在遗传操作中一般都是用最优保存策略，也就是把当前种群中最好解保存起来与下一代种群的所有个体的适应度相比较，如果有更好的个体，则将该个体替换所保存的个体，否则不替换。

为了加快进化速度，提高计算结果的实时性，我们设计了一个采用实数编码多子种群并行进化的遗传算法，算法的主要思想是：采用实数编码，将整个种群分成N(N≥2)个子群，每个子群各自独立遗传进化，在当前种群中所有子群都进化完毕时，将各自保存的最优解比较得到整个种群在当前代的最优解并保存。然后进入下一代遗传操作，如此反复，直到最大进化迭代次数为止，输出最终保存的最优解。

3.1.1初始种群的选取

根据问题DNLOP(T)的约束域，按照均匀分布随机产生算法的初始种群。

3.1.2适应度评价函数的选取

算法中个体的适应度用来表示该个体适应环境的能力，同时也表示其繁殖后代的能力。适应度越大表明该个体适应环境和繁殖后代的能力越强，又因为适应度函数在比较排序的基础上计算选择概率，所以适应度评价函数要取正值。因此在本文中我们采用如下的适应度评价函数，即

3.1.3选择算子

采用无回放随机选择算子，即根据种群中个体在下一代种群中的生存期望值进行选择，具体选择步骤如下：

步1：计算个体xi的生存期望值

步2：如个体xi未被选中，则令Ei=Ei-0.5；否则Ei=Ei-1；

步3：若种群中某个体的生存期望值小于等于零，则淘汰该个体，并使用最优保存策略将上一代的最优个体代替该个体。

3.1.4交叉算子

采用启发式交叉算子，设x(t)和y(t)为第t代进行交叉运算的两个指定个体，则两个子代个体的第j个分量的交叉运算公式为

xj(t+1)=xj(t)+λ[xj(t)-yj(t)]，

yj(t+1)=xj(t)-λ[xj(t)-yj(t)]。

3.1.5变异算子

采用非均匀变异算子，设对个体x(t)的第j个分量xj(t)进行变异操作，其中又知xj(t)∈[U,L]，U和L分别为xj(t)的上下界，则

其中Δ(t,w)=w(1-r(1-t/s)θ)，这里的S为最大进化迭代次数，r是(0,1)内均匀产生的随机数，θ是系统参数，决定着算法的收敛压力。

3.1.6算法终止条件

若算法完成最大进化代数且问题的最优值连续n代无变化则算法停止，输出最优解。

综上，设计算法的主要步骤如下。

步1：设定最大迭代次数为S，种群规模为M，交叉概率为pc，变异概率pm，子群组数为N，并保证N能整除M，令t∶=0；

步2：在约束域中随机生成M个初始个体，把整个种群分成N个子群；

步3：计算各子群中所有个体的适应度值，并对每个子群进行交叉，变异，选择操作，

步4：将各子群的最优个体比较并保存整个种群的最优个体；

步5：若满足终止条件，则算法停止输出保存的最优解，否则令t∶=t+1，转步3。

算法的收敛性分析如下：采用最优保存策略的遗传算法已经被证明能够以概率1收敛到问题的近似最优解[14-15]。在种群的初始化阶段，因种群的所有个体都是在问题的约束域中随机生成，所以在该阶段的时间复杂度为O(M)，在算法的运行阶段，由算法的第三步，可知时间复杂度为O(S×M)。综合两个阶段可知，该算法的时间复杂度为O(S×M)。

3.2数值算例

设使用甲、乙、丙三种有限资源生产A，B，C，D四种产品，产品的资源消耗系数由表1给出，四种产品的需求函数分别为：p1=8-⊗1x1，p2=

9-⊗2x2，p3=10-⊗3x3和p4=11-⊗4x4，其中x1，x2，x3和x4分别为四种产品的生产量，⊗为灰色系数。资源甲和乙在一个生产周期内可供应量分别为200单位和300单位，资源丙的供应量是由时间序列描述，见表2。问在第6周期应如何安排生产计划，才能使工厂的总收益最大？

表1　产品的资源消耗系数

表2　资源丙供应量的时间序列

解对该问题建模可得如下灰色非线性优化问题：

maxf(x,⊗)=(8x1+9x2+10x3+11x4)-

其中⊗1∈[0,0.02]，⊗2∈[0.01,0.03]，⊗3∈[0.03,0.05]和⊗4∈[0.02,0.08]。

约束中r(t)的时间序列经检查均满足准光滑条件和准指数规律，故按照第2节的方法进行GM(1,1)建模，得

则有

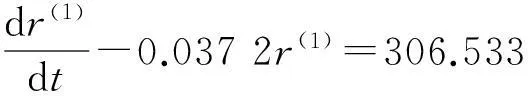
时间响应式为

进而可预测第6周期资源丙的供应量为375。将问题均值白化以后可得如下确定性非线性优化问题：

maxf(x)=(8x1+9x2+10x3+11x4)-

使用多子种群遗传算法进行求解，设定最大迭代次数为S=200，种群规模为M=80，交叉概率为pc=0.7，变异概率pm=0.2，子群组数N=2。使用MATLAB 2010a平台编程求出最优解为x=(0,9.592,20.376,50.661)，最优效益预测值为700.586。

4结语

针对灰色非线性优化问题的灰色预测数学模型，基于GM(1,1)模型对约束中的参数时间序列进行预测，并使用均值白化模型将其转化为确定型的非线性优化问题，进而设计了一个多子群遗传算法，实际算例表明求解策略和算法是可行的。

参考文献:

[1] 马良荔, 李刚, 陶道强. 基于灰色GM(1,1)模型的故障预测方法[J]. 计算机应用与软件, 2013, 30(4): 198-200.

[2] 曾振东. 基于灰色支持向量机的网络舆情预测模型[J]. 计算机应用与软件, 2014, 31(2): 300-302, 311.

[3] 李茂达, 樊磊, 李磊, 等. 隧道与地下工程围岩变形的灰色优化与预测[J]. 土木建筑与环境工程, 2013, 35(S2): 143-145.

[4] 张岐山, 陈华, 刘虹. 灰需求下供应链配送网络优化研究[J]. 中国管理科学, 2013, 21(S1): 26-30.

[5] 杨悦. 基于离散灰色模型的优化方法研究[J]. 科学技术与工程, 2013, 13(26): 7856-7861.

[6] 王渭明, 王国富, 冯玉国. 三角模糊数型多属性决策灰色优化模型及其在工程设计方案评价中的应用[J]. 数学的实践与认识, 2012, 42(12): 21-27.

[7] 邓聚龙．灰色多维规划[M]．武汉: 华中理工大学出版社, 1988.

[8] 张曙红, 陈绵云. 灰色非线性规划问题及其遗传算法求解方法[J]. 系统工程理论与实践, 2002, 22(7): 128-130.

[9] 刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2010.

[10] 何勇. 灰色线性和非线性规划的一种通用解法[J]. 科技通报, 1988, 4(4): 16-19.

[11] 刘兵兵, 郭亚君. 灰色多随从二层线性规划问题及其解法[J]. 吉林大学学报(理学版), 2011, 49(04): 625-632.

[12] 刘兵兵. 一类灰色二层线性多目标规划问题及其算法[J]. 山东大学学报(理学版), 2012, 47(5): 122-126.

[13] 周伟平, 刘兵兵. 解灰色非线性规划问题的一种随机搜索算法[J]. 计算机应用, 2013, 33(10): 2819-2821.

[14] 徐宗本, 陈志平, 章祥荪. 遗传算法基础理论研究的新近发展[J]. 数学进展, 2000, 46(2): 97-114.

[15] 张文修，梁怡. 遗传算法的数学基础[M]. 西安: 西安交通大学出版社, 2000.

A Multi-subgroup Genetic Algorithm for Solving GM (1, 1)Model of Nonlinear Optimization Problem

LIU Bing-bing， HAO Qing-yi

(School of Mathematics and Computation Science, Anqing Teachers College, Anqing 246133, China)

Abstract:According to the historical data of the time series of the constraints parameters in the nonlinear optimization problem, the values of the constraints parameters are modeled and predicted using GM(1,1) method. Substituting the predicted values of the parameters into the grey nonlinear optimization problem, we obtain a determinate nonlinear optimization problem. Then, we design a multi-subgroup genetic algorithm genetic algorithm to solve the resulting problem. Moreover, we analyze the convergence of our method and develop preliminary the numerical experiment which shows that the (approximated) global optimal solution of the predicted nonlinear optimization problem can be found using the proposed method.

Key words:GM(1,1) model，nonlinear optimization problem，mean whitenization，multi-subgroup genetic algorithm，global optimal solution

文章编号：1007-4260(2015)03-0026-05

中图分类号：TP391.9

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.008

作者简介：刘兵兵，男，河北武安人，硕士，安庆师范学院副教授，研究方向为优化理论与方法。

基金项目：安徽省高校省级自然科学基金重点项目(KJ2014A139)。

收稿日期：2014-12-09

郝庆一，男，安徽霍邱人，博士，安庆师范学院副教授，主要研究领域为博弈论及其应用。

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.008.html