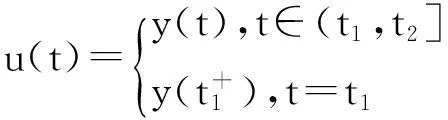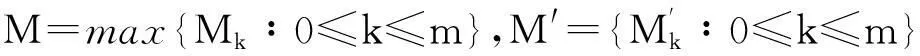Banach空间中二阶非线性脉冲微分方程初值问题解的存在性

张 海 燕

(宿州学院 数学与统计学院, 安徽 宿州 234000)



Banach空间中二阶非线性脉冲微分方程初值问题解的存在性

张 海 燕

(宿州学院 数学与统计学院, 安徽 宿州 234000)

摘要：利用Monch不动点定理和分段估计方法, 结合Gronwall不等式, 研究了Banach空间中一类二阶非线性脉冲微分方程初值问题解的存在性。 将该问题转化为等价的一阶非线性脉冲积分方程, 在较弱的非紧性条件和先验估计条件下, 获得了其解的存在性充分条件, 改进和推广了相关文献的结果。

关键词：脉冲微分方程；初值问题；不动点定理； 非紧性测度

脉冲现象作为一种瞬时突变现象，其数学模型可归结为脉冲微分系统。这类脉冲系统在人口动力系统、经济学、物理学和控制理论等学科中有具体的模型应用。本文考虑实Banach空间中二阶非线性脉冲微分方程初值问题(IVP)：

(1)

1预备知识和引理

J′=J{t1,t2,…,tm},J0=[0,t1],J1=(t1,t2],…,Jm-1=(tm-1,tm]，

Jm=(tm,a],Tr={x′∈E|‖x′‖PC≤r},

Br={x∈PC1[J,E]|‖x‖PC1≤r}。

若x∈PC1[J,E]∩C2[J′,E]满足(1)式，则称x是(1)的解。对Banach空间中的有界集V用α(V)来表示V的Kuratowskii非紧性测度,有关非紧性测度的定义及性质参见[6]。为了后文表述方便，首先给出下列引理：

引理1[7]设H={xn}⊂L[J,E]且存在

g∈L[J,R+],使得对一切

xn∈H,‖xn(t)‖≤g(t),a.e.,t∈J，

2主要结果

为方便起见，先列出下列条件

(H1)对任何r>0,f在J×Tr×Tr×Tr上一致连续，Ik在Tr上有界。

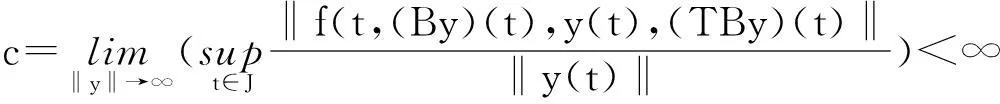
(H3)存在Mi≥0(i=1,2,3)，使得对任何H⊂Br,t∈J有α(t(t,(BH)(t),H(t),(TBH)(t))≤M1α((BH)(t))+M2α(H(t))+M3α((TBH)(t))

定理1设条件(H1)-(H3)满足，则IVP(1)在PC1[J,E]∩C2[J′,E]中至少有一个解。

证明IVP(1)等价于一阶非线性脉冲微分方程组

(2)

IVP(2)等价于非线性脉冲积分方程组

(3)

IVP(3)等价于一阶非线性脉冲积分方程

(4)

则IVP(1)与积分方程(4)的解等价。而积分方程(4)的解等价于算子A有不动点，即存在y∈PC[J,E]，使得(Ay)(t)=y(t)。由(H1)和(H3)易知A∶PC[J,E]→PC[J,E]是连续算子。

下面利用Monch定理证明算子A有不动点。首先由假设(H2)知存在β>c和N>0使得

‖f(t,(By)(t),y(t),(TBy)(t)‖<β‖y(t)‖,

t∈J,‖y(t)‖>N，

再由(H1)中f的一致连续性可知

‖f(t,(By)(t),y(t),(TBy)(t)‖<

β‖y(t)‖+G,t∈J

(5)

其中G=sup{‖f(t,(By)(t),y(t),(TBy)(t)‖∶t∈J,‖y(t)‖

下证Ω0={y∈PC[J,E]|y=λAy,0≤λ≤1}是PC[J,E]中的有界集。对任给y∈Ω0，则存在0≤λ0≤1，使得y(t)=λ0(Ay)(t)。

当t∈J0=[0,t1]时，由(4)(5)式得

(6)

故由(6)式和Gronwall不等式知

‖y(t)‖≤(‖y0‖+Gt1)eβt1=M0

‖I1((By)(t),y(t))‖≤β0

(7)

于是由(4)式和(7)式得

M0+β0

(8)

I1((By)(t1),y(t1))]

(9)

于是由(5)，(7)~(9)式得

‖u(t)‖≤‖y0‖+(1+t1)β0+

(10)

由(10)式和Gronwall不等式知

‖u(t)‖≤[‖y0‖+(1+t1)β0+

(t2-t1)G]eβ(t2-t1)=M1

故‖y‖PC≤M1,t∈J1。

以下验证满足引理2的两条件。首先取R>M″=max{M,M′}，令Ω={y∈PC[J,E]|max{‖y‖PC,‖By‖PC}

当t∈J0=[0,t1]时，由非紧性测度的性质、(4)式和假设(H3)以及引理1有

M3α((TBH)(s))]ds

(11)

因为BH,TBH在每个区间Jk上都是等度连续的有界集，所以由引理1得

(12)

将(12)式代入(11)式知

(13)

于是由(13)式和Gronwall不等式有

α(H(t))=0,t∈J0

(14)

当t∈J1=(t1,t2]时，由(13),(14)式可得

α(I1(BH)(t1),H(t1))=

M3(t2-t1)k0(t-s)α(H(s))]ds≤

(15)

由(15)式及Gronwall不等式,知α(H(t))=0,

3小结

文[1-3]在讨论IVP(1)时，使用了脉冲项紧性条件和非紧性测度的先验估计限制性条件。本文利用分段估计方法，去掉了上述条件，获得一般情形下IVP(1)解的存在性结果，本质上推广和改进了文[1-3]的结果。

参考文献:

[1] L.Liu. Iterative method for solutions and coupled quasi-solutions of nonlinear integro-differential equations mixed type in Banach spaces[J]. Nonlinear Analysis, 2000, 42(4): 583-598.

[2] G.Song. Initial value problems for systems of integro-differential equations in Banach spaces[J]. Journal of Mathematical Analysis and Applications, 2001, 264(1): 68-75.

[3] 蔡增霞, 刘立山, 焦圣华, 等. Banach 空间一阶脉冲微分积分方程组初值问题的解[J]. 数学研究, 2007, 40(2): 164-172.

[4] 李耀红, 张晓燕. Banach空间中一类二阶非线性脉冲积分-微分方程边值问题解的存在性[J]. 应用数学, 2011, 24(1): 112-119.

[5] 张晓燕. Banach 空间中一阶非线性脉冲积分-微分方程初值问题[J]. 系统科学与数学, 2011, 30(12): 1695-1703.

[6] D.Guo, V.Lakskmikantham. Nonlinear problems in abstract cones[M]. New York : Academic press, 1988: 1-137.

[7] H.Heinz. On the behaviour of measure noncompactness with respect to differentiation an integration of vectorvalue functions[J]. Nonlinear Analysis, 1983, 7(12): 1351-1371.

[8] K.Deimling. Nonlinear functional analysis[M]. Berlin: spring-Verlag, 1985: 203-215.

Existence of Solutions for a Class Initial Value Problems of Second-Order Nonlinear Impulsive Differential Equations in Banach Spaces

ZHANG Hai-yan

(School of Mathematics and Statistics, Suzhou University, Suzhou 234000, China)

Abstract:By using the Monch fixed theorem and a piece wise estimation method, and combining with a Gronwall inequality, a class initial value problems of second-order nonlinear impulsive differential equations in Banach Spaces is investigated, which can be reduced to the equivalent first-order nonlinear impulsive integral equation. Under weaker noncompactness and priori estimate conditions, some sufficient results on the existence of solution for the initial value problem are established. Some known results are extended and improved.

Key words:impulsive differential equations, initial value problems, fixed point theorem, measure of noncompactness

文章编号：1007-4260(2015)03-0019-03

中图分类号：O175.8

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.006

作者简介：张海燕，女，安徽灵璧人，硕士，宿州学院数学与统计学院副教授，主要从事非线性泛函分析及研究。

基金项目：安徽省教育厅自然科学基金重点项目(KJ2014A252)。

收稿日期：2015-02-02

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.006.html