不同体系斜拉桥车桥耦合共振效应研究

2015-03-11王凌波马印平蒋培文周勇军

合肥工业大学学报（自然科学版） 2015年10期

王凌波，马印平，蒋培文，周勇军，任伟

（1.长安大学公路学院，陕西西安 710064；2.陕西省交通厅基本建设工程质量监督站，陕西西安 710075）

国外学者早在20世纪之前便开始对铁路车桥耦合振动进行研究，通过采用忽略惯性力等近似手段建立车桥振动方程并求解，结果与实际情况较为吻合，但误差依然存在。文献［1－2］对客运专线和高速铁路桥梁车桥相互作用的理论及其应用进行了较系统的研究，先后建立了各具特色的车桥振动分析模型，使车桥耦合振动的研究取得了巨大的进展。国内的车桥耦合振动研究也起始于铁路桥梁。文献［3］以列车荷载通过悬索桥为工程背景，进行了桥梁的强迫振动等方面的研究；文献［4］介绍了车辆与结构动力相互作用的分析理论、分析方法及其工程应用。而对于公路桥梁，由于公路交通荷载较小，早期的研究忽略车桥振动问题。随着我国公路交通建设的飞速发展，车辆载重及行驶速度均显著提高，公路桥梁的车桥耦合振动问题已逐渐受到国内外众多学者的广泛关注。文献［5］以大跨斜拉桥为研究对象，应用拉索侧向振动影响的车桥耦合振动分析方法研究了钢索和碳纤维增强复合材料（carbon fiber reinforced polymer plastic，CFRP）索斜拉桥的交通振动响应，比较了车辆计算模型、行车速度对计算结果的影响，并分析了斜拉桥的动力冲击系数。文献［6］采用移动振动模型，考虑了桥梁的几何非线性影响因素，建立车桥耦合系统的运动微分方程，并分析了非线性因素对桥梁跨中最大位移的影响，探讨了车速、车辆质量、桥梁阻尼和桥梁跨径等参数对振动的影响。文献［7］将桥梁简化为两端简支的欧拉－伯努梁模型，以桥面结构表面不平度功率谱密度函数作为输入，建立了多个移动车辆系统与桥梁的耦合力学分析模型，并结合算例分析了在不同桥梁跨度、不同桥面等级、不同车辆移动速度下桥梁跨中位移均方根值响应的变化规律。文献［8－9］针对主梁刚度下降对车桥耦合振动响应的影响问题，提出基于ANSYS单一环境下的车桥耦合振动响应数值分析方法，在ANSYS环境下通过APDL编程语言实现耦合关系，得到了振动时程响应曲线；文献［10］提出了连续刚构桥的车桥耦合共振效应判定方法。

1 车桥振动及共振问题

由于公路交通事业的迅猛发展，车速、车重、车流量与日俱增，近年来公路桥梁的车桥振动问题逐步受到学者们的关注，车桥振动研究、地震研究、风振研究已成为目前桥梁振动3大主要研究方向。车桥振动分析具体又可分为模态分析、动态响应分析、共振效应分析等几个方面［11］。

车桥耦合模态分析通常将单车辆或多车辆简化为质量－弹簧－阻尼系统，固定于桥面指定位置，并计算车桥系统耦合振动模态，该分析计算过程相对简单，可直观地体现出桥面车辆的存在对桥梁模态的影响。研究结果表明，车辆位置相同时，车桥频率比与车桥质量比是影响桥梁模态变化的主要参数，车桥频率比越接近1，车桥质量比越大，车桥系统模态变化越大［12］。

车桥耦合动态响应分析是车桥耦合振动研究的重点所在，从移动荷载模型、移动质量模型到弹簧－质量模型甚至全车模型，从公式解析法到数值求解法，对车桥耦合动态响应分析的研究已有上百年的历史。车桥耦合振动响应分析较为复杂，可模拟车辆过桥全过程，从而获得任意位置处的挠度、弯矩等响应的动态变化曲线，进而可对冲击系数等参数的变化规律进行研究［13］。

共振效应分析中，行人的质量相对于桥梁结构几乎可忽略不计，故对行人过桥时的动态响应分析较少，然而大队人群齐步过桥时可能引起桥梁的剧烈晃动甚至损伤、坍塌。究其原因，并不是人群质量超限，而是由于齐步频率与桥梁固有频率接近从而产生共振，导致荷载效应成倍增长。鉴于此，许多国家的军队都规定大队人马过桥时，改齐步走为便步走。综合以上研究可以发现，无共振现象时的桥梁动态效应与静态效应相比增量通常不大，而共振产生时该增量却可达几倍甚至几十倍［14］。

对于单车辆或某种形式的车流过桥时产生共振的问题，目前的研究成果表明，简支梁结构在现有车辆技术参数下不可能产生共振，而高墩柔性连续刚构桥在单车辆或等间距车流作用下均有可能发生共振［10，15－16］，而对于斜拉桥、悬索桥等复杂桥梁的车桥共振研究很少，应该加强研究。共振虽属于小概率事件，一旦出现却影响巨大，值得对其发生的可能性进行理论分析及试验研究，并提出相应的预防措施。

目前车桥耦合振动的研究主要针对结构的动态响应分析，而对于共振效应的研究却少有提及［17］。荷载集度并不大的风、人群、地震等因素都曾因与结构物自振频率接近，从而出现共振现象并造成严重后果，对公路车流是否与各种桥型产生共振的可能性研究应给予足够重视，防范于未然，避免车桥共振现象带来的负面效应。

公路斜拉桥跨越能力较大、施工技术较成熟，在我国大跨径桥梁中已占有较大比例。公路斜拉桥的风振、地震响应研究成果较多，而其车桥耦合振动响应研究往往由于车辆荷载较小、大跨结构冲击系数较小而被忽略。由于共振效应会使荷载效应成倍增长，故即使公路车辆静力荷载效应相对较小，对其进行车桥耦合共振效应研究亦有十分重要的意义。车桥耦合振动的数值求解研究已较为成熟，本文将桥梁与车辆模型均独立建立在ANSYS环境下，其耦合作用关系通过APDL编程语言计算并将其在任意时刻施加于车辆及桥梁结构，最终得到振动的时程响应，进而对常见的漂浮体系、半漂浮体系斜拉桥进行车桥耦合共振效应的研究。

2 不同体系斜拉桥车桥耦合共振效应

斜拉桥按照结构体系主要分为漂浮体系、半漂浮体系和塔梁固结体系、刚构体系4种，本文以漂浮体系与半漂浮体系2种常见结构体系为背景，研究各种体系斜拉桥出现车桥共振的可能性及判定条件。由于单车辆产生的荷载效应与斜拉桥设计荷载相比较小，即使冲击系数较大对桥梁的安全性也无较大影响，且行驶车辆通过桥梁的时间有限，不会产生长时间的共振响应，故本节以车流为研究对象，研究车桥共振现场。对于车流量基本饱和时的高速公路，驾驶员保持的安全车间距较为接近，小轿车流或特殊车队行进时，车重亦较为接近，故在此取对车桥共振响应较为不利的等间距车辆组成的车流为对象，研究公路斜拉桥的车桥耦合振动响应及共振判定条件。

2.1 桥梁与车辆模型

以某座全长670m的大跨径双塔公路斜拉桥为研究对象，其边跨各设置1个辅助墩，全桥跨径组合为（50＋120＋330＋120＋50）m，桥塔采用钻石形混凝土桥塔，塔高135m，塔顶至加劲梁距离100m。根据漂浮体系、半漂浮体系的结构特点，在塔梁连接处建立相应边界条件，该斜拉桥有限元模型如图1所示。车流中的行驶车辆采用五自由度三轴车辆模型，如图2所示，车辆技术参数见表1所列。

图1 桥梁有限元模型

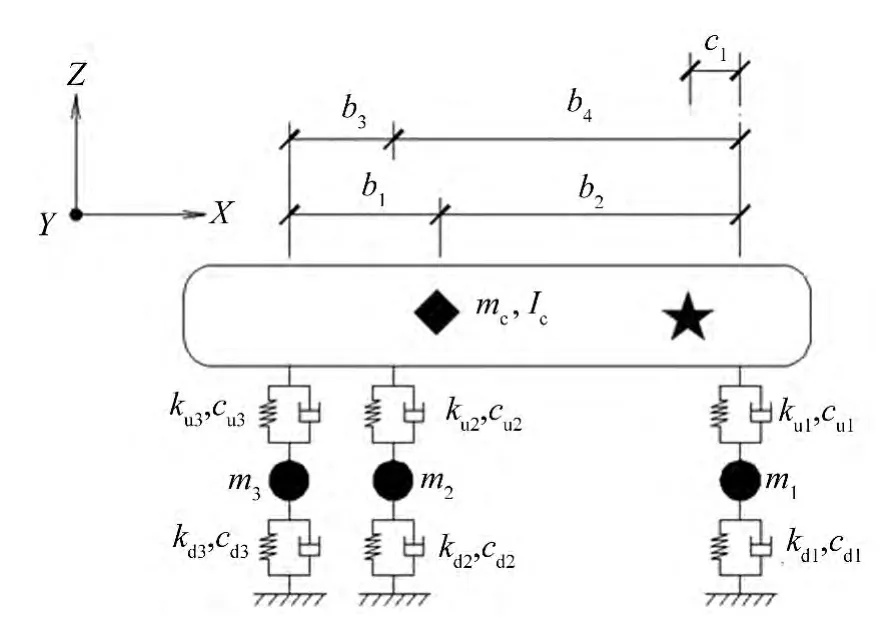
图2 五自由度三轴车辆模型

图2中，mc为车体质量；Ic为车体质心绕z轴转动惯矩；mi、kui、cui、kdi及cdi（i＝1，2，3）分别为各车轮处的质量、刚度及阻尼参数；b1、b2分别为车体质心距后轴、前轴的距离；b3、b4分别为中轴距后轴、前轴的距离；c1为驾驶员位置处距前轴的距离。

表1 三轴车辆参数

2.2 公路斜拉桥车桥共振判定方法及算例

对于多车辆组成的车流荷载，计算结果表明，不同车辆与不同车间距组成的“杂乱车流”产生车桥共振概率极小，本文着重讨论了对于车桥共振效应较为不利的相同车型等间距过桥工况。由于车辆为等间距布置，当车流布满全桥时，t0时刻桥面的车辆位置与t0＋t时刻完全一致，如图3所示（t为车辆行驶1个车间距所需时间）。由此可见，等间距车流对桥梁的荷载效应以车辆间隔时间t为周期，即车流对桥梁的激扰频率fv＝v／sv，其中，v为车辆行驶速度；sv为相邻车辆纵向间隔距离。

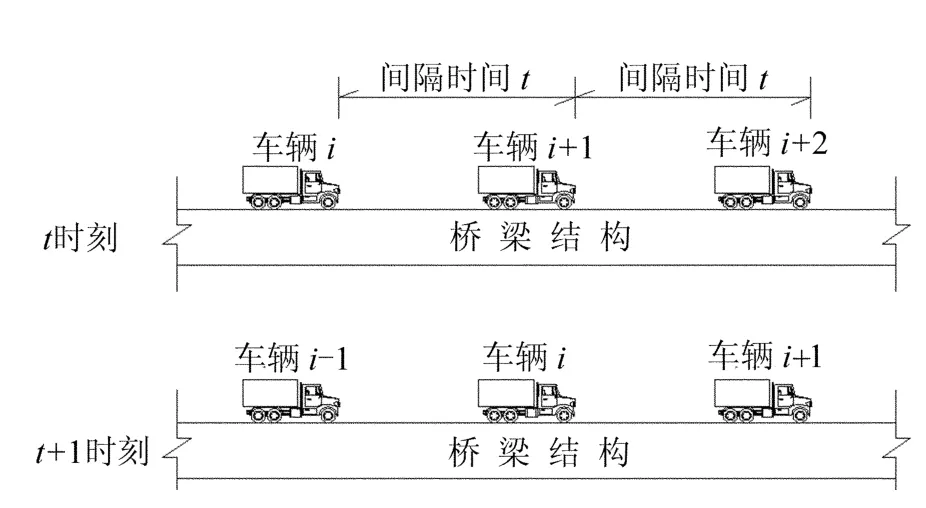
图3 不同时刻车辆位置对比

由以上分析可得，当车辆激扰频率fv与桥梁基频fb接近时结构会产生较明显的共振效应，反之则不会产生明显共振。对于漂浮体系及半漂浮体系斜拉桥，其基频fb及对应的振型如图4所示。

以图1桥梁与图2车辆模型为例，采用本文方法对不同工况下的车桥耦合振动进行分析，各工况计算参数见表2所列，各工况时程响应分析结果如图5所示。

图4 不同漂浮体系一阶振型

表2 车桥共振计算工况

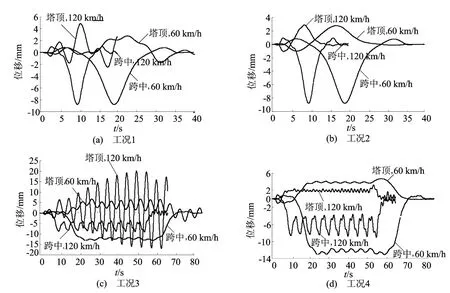
图5 不同工况下的时程响应

由图5可知，实漂浮体系斜拉桥由于基频较小，可能与等间距车流产生共振现象，而半漂浮及其他体系斜拉桥通常基频较大，等间距车流以安全范围内的车间距行驶时的激扰频率无法与其接近，故不会产生共振现象。由于漂浮体系斜拉桥基频对应振型主要体现在桥塔位移，加劲梁位移很小，故桥塔响应的共振现象十分明显，而加劲梁共振现象不明显。现行规范中结构的冲击系数随结构基频降低而减小，但考虑共振效应后的漂浮体系斜拉桥（尤其是桥塔动态响应）并不满足该规律。等间距车流作用下，对桥梁的激扰频率主要由行驶车辆纵向间隔时间确定，车辆分析模型及桥面平整度对冲击系数有影响但不改变共振状态，移动车辆的自身振动频率对共振状态影响极小。

3 结束语

本文提出一种基于ANSYS单一环境下的车桥耦合振动数值求解方法，该方法将桥梁与车辆模型均建立在ANSYS环境下，但两者之间无任何直接联系，两者间耦合作用关系通过APDL编程语言计算，并将其在任意时刻施加于车辆及桥梁结构，最终得到振动响应曲线。该方法易于操作，结果精度较高。通过与既有文献及实桥测试的结果对比验证了本文方法的正确性，为公路复杂桥型的车桥耦合振动研究提供了一种可行的数值方法。

本文提出了等间距车流与斜拉桥发生共振响应的判定方法，对漂浮体系及半漂浮体系斜拉桥在不同工况下的车桥耦合振动响应及共振状态进行了算例分析，共振响应判定结果吻合良好。为防止结构产生共振，建议漂浮体系斜拉桥运营时可在桥面各车道纵向不同位置分别设置减速标志，将车流“打乱”，减小共振概率。对于特殊状况下的车队，过桥时尽量分散行驶于各车道，避免单车道等间距行驶而与桥梁产生共振。

［1］ Dahlberg T.Vehicle－bridge interaction ［J］.Vehicle System Dynamics，1984，13（1）：187－206.

［2］ Diana G，Cheli F.Dynamic interaction of railway systems with large bridges［J］.Vehicle System Dynamics，1989，18（1）：71－106.

［3］李国豪.桥梁结构稳定与振动［M］.北京：中国铁道出版社，1983：386－420.

［4］夏禾，张楠.车辆与结构动力相互作用［M］.北京：科学出版社，2002：186－253.

［5］谢旭，朱越峰，申永刚.大跨度钢索和CFRP索斜拉桥车桥耦合振动研究［J］.工程力学，2007，24（Z1）：53－61.

［6］肖勇刚，朱素红.车桥耦合系统的非线性动力分析［J］.振动与冲击，2007，26（8）：104－108.

［7］叶茂，谭平，任珉，等.多个车辆荷载作用下桥梁演变随机振动分析［J］.振动工程学报，2010，23（3）：269－274.

［8］蒋培文，贺拴海，宋一凡，等.简支梁车桥耦合振动及其影响因素［J］.长安大学学报：自然科学版，2013，33（1）：60－66.

［9］蒋培文，贺拴海，宋一凡，等.大跨径连续梁多工况车桥耦合振动规律分析［J］.武汉理工大学学报，2011，33（7）：62－67.

［10］蒋培文.公路大跨径连续体系桥梁车桥耦合振动研究［D］.西安：长安大学，2012.

［11］陈榕峰.公路桥梁车桥耦合主要影响因素仿真分析方法研究［D］.西安：长安大学，2007.

［12］崔圣爱.基于多体系统动力学和有限元法的车桥耦合振动精细化仿真研究［D］.成都：西南交通大学，2009.