基于FLAC3D地铁车站基坑开挖的变形规律研究

杨 伦， 朱大勇， 袁海平， 蒋泽锋

（1.合肥工业大学 土木与水利工程学院，安徽 合肥 230009；2.土木工程结构与材料安徽省重点实验室，安徽 合肥 230009）

随着城市建设的不断发展，城市交通变得更加拥挤，因此大力开发和利用地下资源，不断发展地下交通，缓解地面交通压力已成为趋势。我国大中城市都在新建或准备新建地铁，地铁建设已成为城市可持续发展的重要组成部分，这就涉及深基坑工程。虽然研究人员对深基坑的变形规律进行了较为深入的研究［1－7］，但我国深基坑工程的理论研究仍需加强，以指导工程实践。本文依托合肥轨道交通2号线潜山路车站深基坑工程，将FLAC3D有限差分软件模拟和监测方法相结合，对地铁车站围护结构的变形规律进行了研究。

1 工程概况

合肥轨道交通2号线西起长宁大道口，东至大众路口，沿长江路敷设。设计全长27.764km，全线为地下线。潜山路站为2、3号线换乘车站，位于长江西路与潜山路交叉路口，车站周边主要以科教用地与居住用地为主。潜山路站起讫里程：YDK24＋282.314～YDK24＋507.901，有效站台中心里程为YDK24＋438.899。车站总长为224.12m，有效站台长为120m，标准段宽度21.4m，最大开挖深度26m，为地下3层岛式车站。本车站主体结构和附属结构拟采用明挖顺筑法施工，采用φ1 000＠1 200钻孔灌注桩，桩长31.5m，设置900×800钢筋混凝土支撑和φ＝600、壁厚t＝16mm的钢支撑，主体围护结构的剖面如图1所示。根据岩土工程勘察报告提供各土层物理力学指标见表1所列。

图1 主体围护结构剖面图

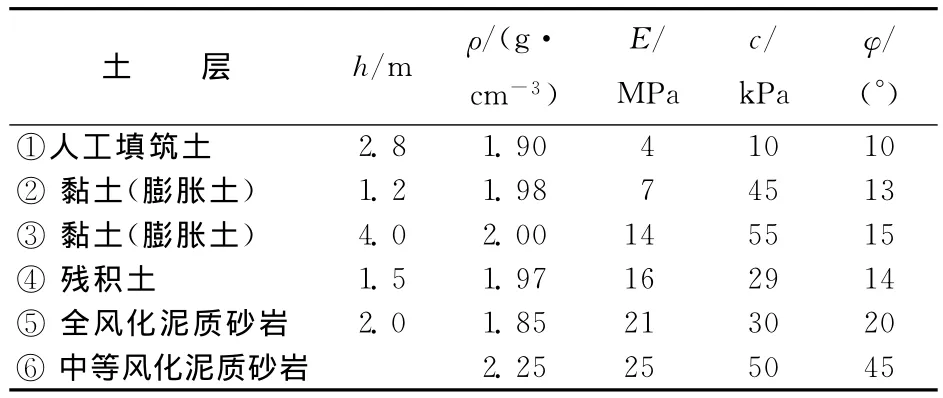
表1 岩土物理力学参数

2 施工工序

基坑施工共分为1个初始平衡步和5个开挖步，具体计算步骤如下：① 考虑围护结构和立柱桩的初始地力平衡，保留应力场，位移清零；② 开挖第1层土至第1道支撑底面，施工第1道混凝土支撑（－2.0m）；③ 开挖第2层土至第2道支撑底面，施工第2道钢支撑（－9.0m）；④ 开挖第3层土至第3道支撑底面，施工第3道钢支撑（－15.0m）；⑤ 开挖第4层土至第4道支撑底面，施工第4道钢支撑（－21.0m）；⑥ 开挖第5层土至坑底（－26.0m）。

基坑开挖前初始地应力平衡时基坑围护结构及坑内立柱桩采用其实际计算参数，在后续的分析中使用实际的刚度，并通过model null或delete命令模拟施工开挖过程，每步执行计算循环达到稳定状态。

3 数值模拟

3.1 数值模型的建立

采用岩土工程常用FLAC3D有限差分软件进行数值模拟分析。由于基坑是长条形基坑，根据对称性建立基坑1／2模型进行分析，实际开挖长度、宽度与深度分别为92m×22m×26m，建立模型相应的尺寸为180m×144m×80m，建立的三维基坑模型计算单元比较多，现有计算机运算能力有限，为降低计算机运行时间，对基坑模型进行了一定的简化，在模型中选取基坑长边中部标准施工段一檩24m作为模拟对象，计算模型的尺寸为180m×24m×80m，计算模型网格共59 808个单元，66 150个节点，如图2所示。

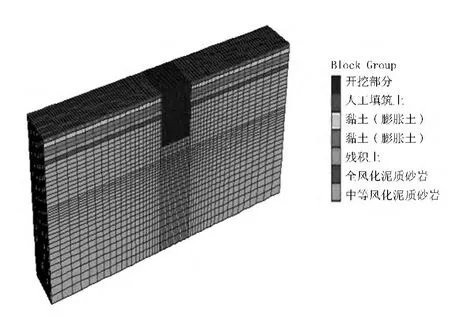
图2 计算模型

土体的计算模型采用摩尔－库伦弹塑性模型，由于钻孔灌注桩围护结构的受力形式与地下连续墙相似，因此本文根据抗弯刚度等效原则，将钻孔灌注桩折算成一定厚度的地下连续墙，用实体单元进行模拟，并将地下连续墙设置为弹性模型［8］。墙土之间的接触面问题可以用接触面单元进行处理，钢筋混凝土支撑和钢支撑用beam单元模拟。

3.2 模拟方案计算工况

本模型分5步开挖，具体步骤如下：① 基坑开挖至－2.0m处设置第1道钢筋混凝土支撑；② 基坑开挖至－9.0m处设置第2道钢支撑；③ 基坑开挖至－15.0m处设置第3道钢支撑；④ 基坑开挖至－21.0m处设置第4道钢支撑；⑤ 基坑开挖至基底－26.0m处。

由于基坑第1步开挖深度比较小，基坑变形不明显，从第2步基坑开挖进行分析，把施工过程分为4个工况进行模拟，开挖工况如图3所示。

4 模拟值与实测值对比分析

4.1 围护结构水平位移分析

本模型以基坑长边中点附近测斜孔CX6为研究对象，基坑分步开挖各工况水平位移云图如图4所示，围护结构各工况水平位移计算结果与实测结果如图5所示。

由图5可以看出，围护结构水平位移模拟值与实测值的分布规律基本一致，且最大水平位移值及位置与实测值略有偏差，实测值比模拟值大，这是由于模拟基坑开挖过程中将围护结构与墙后土体用耦合弹簧方式连成一个整体，较好地约束了围护结构的变形。随着基坑开挖深度的不断增加，围护结构的最大水平位移逐渐增大，形成两端小、中间大的“抛物线形”分布；且最大水平位移逐渐下移，其最大变形位置位于开挖面附近。

由图5可以看出，每个工况下存在水平支撑的地方都会出现拐点，说明水平支撑的存在可以有效地抑制围护结构的变形。拐点的位置并不是水平支撑架设的位置，而是低于其水平支撑1m左右。

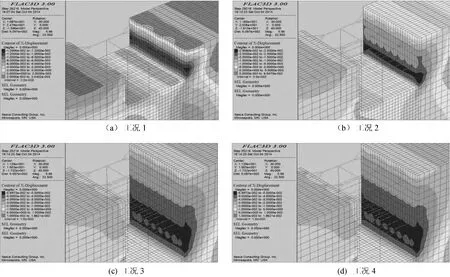
图4 各工况下基坑北侧深层水平位移云图

围护结构水平位移模拟值与实测值的偏差可能是由于在建模时把天然土体每层的厚度取加权平均值，而没有考虑实际的土层分布和地下水的升降对模型的影响；基坑开挖过程中不考虑时空效应和施工过程中对土体的力学性能影响等。

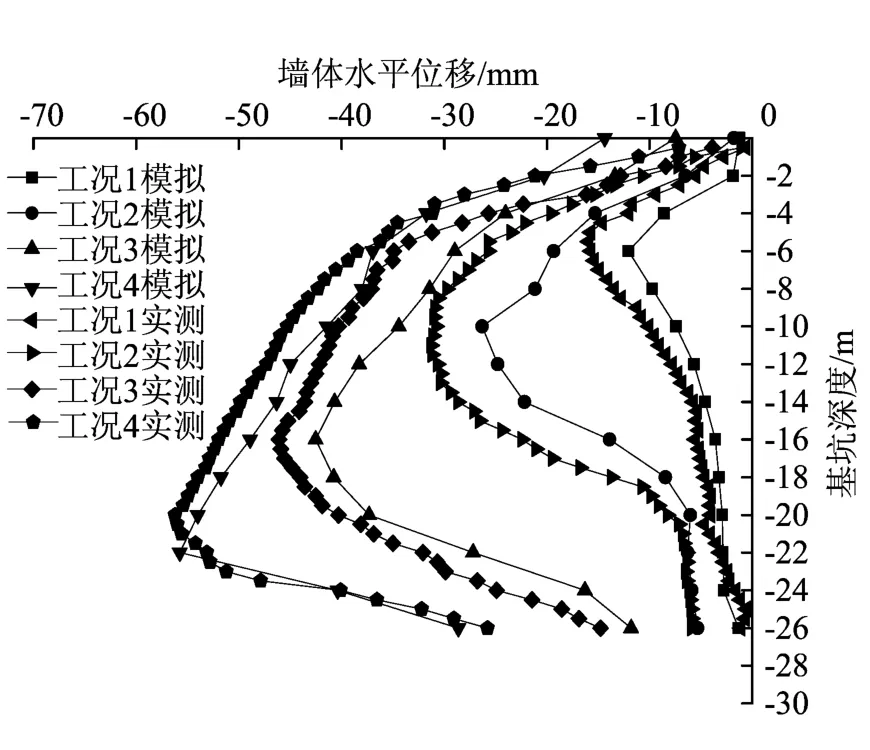
图5 各工况下围护结构水平位移模拟值与实测值

由图5可知，工况1和工况2基坑底部的水平位移为1～6mm，在开挖到基坑底部时位移突增到28mm左右，说明基坑内的土体对围护结构的水平位移具有较强的约束作用。

基坑的开挖都在施工变形的容许范围之内，从总体上看，模拟结果与监测结果变形曲线发展趋势大致相同，初步验证了该模型模拟基坑开挖的可行性。

4.2 基坑外地表沉降分析

基坑分步开挖各工况基坑北侧深层竖向位移云图如图6所示，深层竖向位移计算结果与实测结果如图7所示。

图7表明，地表沉降模拟值与实测值虽然在数值上存在一些差异，但沉降曲线总体的发展趋势大致相同。随着基坑开挖深度的不断增加，地表沉降明显增大，呈“凹槽形”分布。

由图7可以看出，由于监测点的实测数据比较少，曲线并不平滑，地表的最大沉降不是在墙后，而是在距基坑边缘10m左右处。即墙后虽有沉降变形，但其沉降值并非最大，而是随着离基坑边缘距离的增加而逐渐增大，在离基坑边缘10m左右处沉降值达到最大，然后随着离基坑边缘距离的增加沉降值逐渐减小，最后趋近于0。实测最大沉降值的位置相比于模拟值要靠近基坑，而且每步开挖实测最大沉降值比模拟值略大。这是由于模拟值是假设土层均匀分布，与实际土层存在差异；地表实际荷载总是不断变化的，时而超载，时而无载，并且机械的施工不可避免对土体造成扰动，导致土体物理力学参数的改变。此外，模拟值中没有考虑坑外水位变动对其影响，而实测值中包括了这部分的沉降。

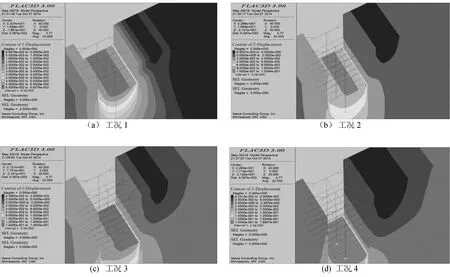
图6 各工况下基坑北侧深层竖向位移云图

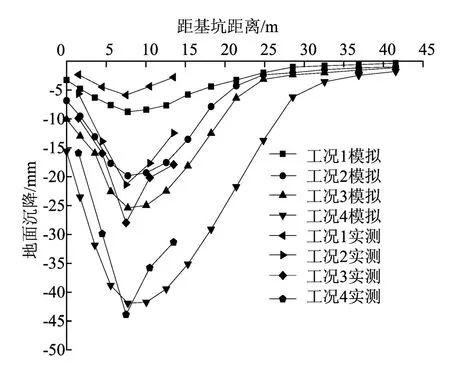
图7 各工况下地表沉降模拟值与实测值

4.3 围护结构变形与周围地表沉降相关性分析

地层损失法［9］认为围护结构变形和地表沉降具有内在关系，从而利用围护结构的水平变形来计算地表沉降。其原理为：墙前土体的挖除破坏了原有力系的平衡状态，墙体向基坑内发生位移，必然导致墙后土体的应力释放和达到新的平衡，引起墙后土体产生位移。文献［10］指出软黏土中支撑基坑的地表沉降的纵剖面图与墙体挠曲的纵剖面基本相同，所以在理想情况下，可以近似地认为地表最大沉降值等于墙体最大水平位移。

下面利用各工况围护结构水平位移曲线和基坑外地表沉降曲线所形成的面积，动态研究支护结构地下连续墙的变形对基坑外地表沉降的影响。以工况1为例，围护结构水平位移和基坑外地表沉降组合曲线所形成的面积如图8所示。

图8 工况1围护结构水平位移和地表沉降计算面积

为了简化计算，采用近似三角形面积法，把不规则的图形面积等效为三角形面积计算。各工况下，墙体水平位移面积Sw和墙后地表沉降面积Sc的计算结果见表2所列。

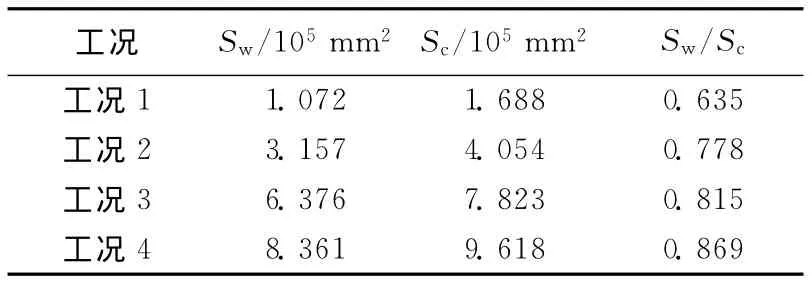
表2 各工况Sw和Sc及其比值

由表2可知，工况1的Sw／Sc值为0.635，工况2的比值为0.778，工况3的比值为0.815，工况1到工况2Sw／Sc值增大的速率较大，工况2到工况3比值增大的速率减缓，说明基坑刚开挖阶段，支护结构还没有完全发挥作用，围护结构水平位移的增速比墙后地表沉降增速快，随着开挖深度的增加，钢筋混凝土支撑和钢支撑对围护结构水平位移的抑制作用越来越明显，导致水平位移增速逐渐减缓。显然，Sw／Sc随着开挖深度的增加，其值是递增的，并逐渐趋近于1。

计算结果表明，Sw／Sc的比值为0.6～0.9时，在各工况下其比值变化幅度不大，并与实测数据的Sw／Sc比 值0.7～0.9比较吻合，由此可认为基坑开挖引起围护结构的变形是导致墙后地表沉降的主要原因。

5 结 论

本文通过FLAC3D有限差分软件对潜山路车站基坑工程施工全过程开挖进行数值模拟，分析得出围护结构的变形曲线呈两端小、中间大的“抛物线”分布，基坑外地表沉降变形曲线呈“凹槽型”分布。模拟值与实测值具有较好的拟合性，其变形规律基本一致，可初步验证本模型模拟开挖是可行的。

随着基坑开挖深度的增加，围护结构水平位移逐渐增大，且最大水平位移逐渐下移，其最大变形位置位于开挖面附近；地表沉降明显增大，且最大沉降不在墙后，而是在距基坑边缘10m左右处。由围护结构变形与周围地表沉降相关性分析可得，基坑开挖引起围护结构变形是导致墙后地表沉降的主要原因。

［1］ Hsiao E C L，Schuster M，Juang C H，et al.Reliability analysis and updating of excavation－induced ground settlement for building serviceability assessment［J］.Journal of Geotechnical and Geoenvironmental Engineering，2008，134（10）：1448－1458.

［2］ 王 伟，程 彦，谭晓慧，等.合肥轨道交通锦绣站深基坑支护监测分析［J］.合肥工业大学学报：自然科学版，2011，34（7）：1031－1034，1049.

［3］ 曹燕霞.深基坑开挖引起变形的数值模拟［D］.武汉：华中科技大学，2008.

［4］ 刘井学，陈有亮，陈剑亮.某深基坑开挖的三维有限元模拟与分析［J］.建筑结构，2007，37（6）：66－68.

［5］ 吕小军，杨 琪，钱德玲，等.非对称超载条件下深基坑支护结构的变形分析［J］.合肥工业大学学报：自然科学版，2012，35（6）：809－813.

［6］ 孙 凯，许振刚，刘庭金，等.深基坑的施工监测及其数值模拟分析［J］.岩石力学与工程学报，2004，23（2）：293－298.

［7］ 张明聚，何 欢，李春辉，等.明挖地铁车站围护结构受力变

形监测与数值模拟分析［J］.北京工业大学学报，2013，39（6）：875－880.

［8］ 陈育民，徐鼎平.FLAC／FLAC3D基础与工程实例［M］.北京：中国水利水电出版社，2008：58－61.

［9］ 刘国彬，王卫东.基坑工程手册［M］.第2版.北京：中国建筑工业出版社，2009：236－239.

［10］ Peck R B.Deep excavation and tunneling in soft ground［C］／／Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering，State－of－the－Art－Volume，Mexico City，1969：225－290.