环Z4＋vZ4上的斜循环码

刘清清， 刘 丽

（合肥工业大学 数学学院，安徽 合肥 230009）

0 引 言

20世纪90年代，文献［1］证明了某些高效二元非线性码可以看作Z4－线性码的Gray象，自此人们对有限环上编码理论的研究产生了浓厚的兴趣，尤其是环上的循环码和常循环码的研究成为编码理论的热点。文献［2－4］第1次提出了利用非交换的斜多项式环来构造一种更广义的循环码，称之为斜循环码，并通过斜多项式环上的码构造出了许多好码；文献［5－6］将有限域上的斜循环码推广到伽罗瓦环和有限链环上；文献［7］通过斜多项式环上模来研究斜循环码及其对偶码的相关性质；文献［8］研究了环F2＋vF2上的斜多项式环的结构，并给出了斜循环码及其对偶码的生成元；文献［9］利用Gray映射讨论了F4＋vF4上斜循环码和环F2＋vF2以及F4上的斜循环码的关系；文献［10］介绍了Fp＋vFp上斜循环码的性质；文献［11－12］研究了有限环Z4＋vZ4（v2＝v）的结构以及该环上的线性码的性质。

本文对环Z4＋vZ4（v2＝v）上的斜循环码进行研究，给出了斜多项式环R［x；θ］的结构与性质以及斜循环码的定义，并证明了R上长度为n的斜循环码C 为R［x；θ］／（xn－1）的左R［x；θ］－子模。最后给出了斜循环码的欧几里得对偶码和厄米特对偶码的定义及其生成多项式，并讨论了斜循环自对偶码存在的条件。

1 预备知识

设R为有限交换环，Rn为环R上n维向量组成的集合。R上长为n的码为Rn的一个非空子集，若它是Rn的一个加法子群或者Rn的R－子容模，则该码为线性码。对于R上长为n的线性码C 中任意的码字c＝（c0，c1，…，cn－1）∈C，它的循环移位（cn－1，c0，…，cn－2）∈C，则称该码为循环码。码C 中每个码字c＝（c0，c1，…，cn－1）均可以对应于R［x］中的一个码字多项式，即

c（x）＝c0＋c1x＋…＋cn－1xn－1。设环R＝Z4＋vZ4＝｛a＋vb｜a，b∈Z4｝，其中v2＝v，该环与多项式环Z4［v］／（v2）同构。环R的单位群U（R）＝｛1，3，1＋2v，3＋2v｝，且R中的非单位元均为零因子。环R为半局部的有限非链环，通过计算R只有2个极大理想〈v＋1〉和〈v＋2〉。故由中国剩余定理知，R＝〈v＋1〉8〈v＋2〉，那么对于任意的α∈R，α可唯一表示成a（v＋1）＋b（v＋2），其中a，b∈Z4。

2 斜循环码

定义环R上非平凡的自同构如下：

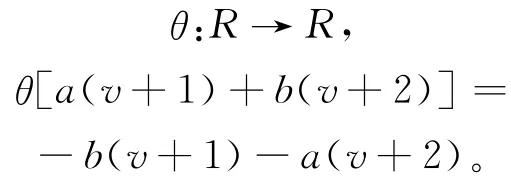
对于任意的α∈R，都有θ2（α）＝α，即θ是阶为2的环自同构。对于任意的e∈Z4，有θ（e）＝e，所以Z4为θ的固定环。

定义1 环R上的多项式集合R［x；θ］＝｛a0＋a1x＋…＋anxn｜ai∈R，0≤i≤n，n∈N｝为斜多项式环，其中加法定义为通常的多项式加法，乘法定义如下：

其中，fs、gt为R 中的单位，则存在R［x；θ］中唯一的多项式p（x）、q（x）使得：

其中，deg（q（x））＜deg（g（x））或者q（x）＝0。若q（x）＝0，则称g（x）为f（x）的右因式，g（x）右整除f（x）。

定理 1 R［x；θ］的 中 心 Z（R［x；θ］）是Z4［x2］。

证明 θ是阶为2的环自同构，对于∀r∈R有x2i＊r＝（θ2）i（r）x2i＝r＊x2i。因此 x2i∈Z（R［x；θ］）。由Z4为θ的固定环可知，f（x）＝f0＋f1x2＋…＋fkx2k为R［x；θ］中心中的一元，其中fj∈Z4，0≤j≤k。反之，对∀f（x）∈Z（R［x；θ］），r∈R，有f（x）＊r＝r＊f（x），x＊f（x）＝f（x）＊x，则

推论1 若xn－1∈Z（R［x；θ］），当且仅当n为偶数。

推论2 若n为偶数，且在R［x；θ］中，xn－1＝g（x）＊h（x），则

xn－1＝g（x）＊h（x）＝h（x）＊g（x）。

证明 参考文献［3］中定理10的证明。

定义2 Rn的子集C叫做斜循环码（也称θ－循环码），若C满足以下条件：

（1）C为Rn的R－子容模。

（2）若 （c0，c1，…，cn－1）∈C，则 （θ（cn－1），θ（c0），…，θ（cn－2））∈C。

若θ为R上平凡的自同构，则定义2的码C为循环码。

令Rn＝R［x；θ］／（xn－1），Rn中的加法为通常的多项式加法，乘法定义如下：

设f（x）∈Rn，对于任意的r（x）∈R［x；θ］，r（x）＊（f（x）＋（xn－1））＝r（x）＊f（x）＋（xn－1），称Rn是左R［x；θ］－模。

定理2 码C是R上长度为n的斜循环码，当且仅当码C是左R［x；θ］－模Rn的左R［x；θ］－子容模。

证明 若码C为斜循环码，则对于∀c＝（c0，c1，…，cn－1）∈C，有（θ（cn－1），θ（c0），…，θ（cn－2））∈C，即f（x）＝c0＋c1x＋…＋cn－1xn－1∈C，则x＊f（x）∈C。由线性可得∀g（x）∈R［x；θ］，g（x）＊f（x）∈C。所以C是左R［x；θ］－模Rn的左R［x；θ］－子容模。

若码C 是左R［x；θ］模Rn的左R［x；θ］－子模，则∀f（x）＝c0＋c1x＋…＋cn－1xn－1∈C，x＊f（x）＝θ（cn－1）＋θ（c0）x＋…＋θ（cn－2）xn－1∈C，即对于任意的c＝（c0，c1，…，cn－1）∈C，（θ（cn－1），θ（c0），…，θ（cn－2））∈C，所以码C为斜循环码。

定理3 设码C是Rn中的斜循环码，f（x）为码C中次数最低的多项式。若f（x）为首一多项式，则C＝（f（x））＝｛r（x）＊f（x）｜r（x）∈Rn｝，其中f（x）为xn－1的右因式。

证明 对于任意的c（x）∈C存在q（x），r（x）∈Rn，使得c（x）＝q（x）＊f（x）＋r（x），其中r（x）＝0或deg（r）＜deg（f）。因为码C 是线性的，r（x）＝c（x）－q（x）＊f（x）∈C。而f（x）为码C中次数最低的多项式，所以r（x）＝0，即c（x）＝q（x）＊f（x）。因此C＝（f（x））。

再证f（x）为xn－1的右因式。存在q1（x），r1（x）∈R［x；θ］，使xn－1＝q1（x）＊f（x）＋r1（x），其中r1（x）＝0或deg（r1）＜deg（f）。所以在Rn中，r1（x）＝－q1（x）＊f（x）∈C。由f（x）为码C中次数最低的多项式得r1（x）＝0，所以f（x）为xn－1的右因式。

引理1 若f（x）是码C中次数最低的但不是首一的多项式，则f（x）＝fkf1（x），其中fk∈R但fk∉U（R），f1（x）为R 中首一多项式。

证明 设f（x）＝f0＋f1x＋…＋fkxk，若fk为单位，则码C中必存在k次首一的多项式，所以fk不为单位。由于环R中的不可逆元均为零因子，可设S＝｛u｜u∈R，ufk＝0｝。对∀a∈S，有af（x）＝af0＋…＋afkxk＝af0＋…＋afk－1xk－1，又由于f（x）是码C中最低次数多项式，af（x）＝0。对∀a∈S，afi＝0，其中0≤i≤k－1，即fi＝fkbi（bi∈R）。故f（x）＝fkf1（x），f1（x）为 R 中首一多项式。

定理4 设码C为环R上的斜循环码，f（x）为码C中次数最低的多项式，如果码C中没有首一多项式，则C＝（f（x）），其中f（x）＝fkf1（x），fk∈R＼U（R）。f1为R 中首一多项式，且f1是xn－1的右因式。

证明 对于∀c（x）∈C，存在R［x；θ］中多项式q（x）和r（x），使c（x）＝q（x）＊f（x）＋r（x），其中r（x）＝0或者deg（r）＜deg（f）。由于f（x）为码C中次数最低的多项式，码C中没有首一多项式，所以r（x）＝0，即C＝（f（x））。

令xn－1＝Q（x）＊f1（x）＋R（x），其中Q（x），R（x）∈R［x；θ］，R（x）＝0或者deg（R）＜deg（f1），易知Q（x）为首一多项式。再令Q（x）＝Q1（x）＋Q2（x），Q1（x）为Q（x）中所有的奇次项，Q2（x）为Q（x）中所有的偶次项，fk＝a（1＋v）＋b（2＋v）。若Q1（x）为首一多项式，那么有：

fk（xn－1）＝fk（Q（x）＊f1（x））＋fkR（x）＝fkQ1（x）＊f1（x）＋fkQ2（x）＊f1（x）＋fkR（x）＝Q1（x）＊θ（fk）f1（x）＋Q2（x）＊fkf1（x）＋fkR（x）＝Q1（x）＊fkf1（x）＋Q2（x）＊fkf1（x）＋fkR（x）＋Q1（x）＊（（a＋b）（1＋2v））f1（x）。

由于码C是斜循环码，在Rn中p（x）＝Q1（x）＊［（a＋b）（1＋2v）］f1（x）＋fkR（x）∈C，所以存在s（x）∈Rn满足p（x）＝s（x）＊fkf1（x），又因为Q1（x）、f1（x）首一且码C 中没有首一的多项式，所以a＋b≠1或3。若a＋b＝2，fk∉U（R），则a＝0，b＝2，fk＝2v或a＝2，b＝0，fk＝2＋2v。当a＝0，b＝2，fk＝2v时，p（x）的最高项系数为2，那么存在r∈R，使得r·θ（2v）＝2或者r·2v＝2，矛盾。当a＝2，b＝0，fk＝2＋2v时，同样是矛盾的。所以a＋b＝0，即p（x）＝fkR（x）∈C。又由f（x）为码C中次数最低的多项式得R（x）＝0。若Q2（x）为首一的多项式，可以通过讨论θ（fk）＊（xn－1）同理可得R（x）＝0，所以f1（x）为xn－1的右因式。

定理5 设码C为Rn中的含有部分首一多项式的斜循环码。假设码C中次数最低的多项式f（x）不为首一多项式，则C＝（f（x），g（x）），其中g（x）是在码C内的首一多项式中次数最低的多项式。

证明 对于任意的c（x）∈C，存在唯一的多项式q（x），r（x）∈R［x；θ］，使得c（x）＝q（x）＊g（x）＋r（x），其中r（x）＝0或者 deg（r（x））＜deg（g（x））。由码C 为斜循环码，g（x）∈C 可知r（x）∈C。如果r（x）＝0，则c（x）∈（f（x），g（x））。如果r（x）≠0，则r（x）不为首一多项式，令r（x）＝q1（x）＊f（x）＋r1（x），其中r1（x）＝0或者deg（r1）＜deg（f），由f（x）是码C中次数最低的多项式知r1（x）＝0，所以c（x）＝q（x）＊g（x）＋q1（x）＊f（x）∈ （f（x），g（x）），故 C＝（f（x），g（x））。

定理6 设码C是R上长度为n的斜循环码，若n为偶数，则码C等价于R上长度为n、指数为2的准循环码；若n为奇数，则码C等价于R上长度为n的循环码。

证明 若n为偶数，对于∀c＝（c0，c1，c2，…，cn－1）∈C，由θ2＝1可知：

θ2（c）＝ （θ2（cn－2），θ2（cn－1），θ2（c0），…，θ2（cn－3））＝（cn－2，cn－1，c0，…，cn－3）∈C。

再由准循环码的定义知，C等价于R上长度为n、指数为2的准循环码。

若n为奇数，对于任意的c＝（c0，c1，c2，…，cn－1）∈C，由斜循环码的定义知：

（θn（c0），θn（c1），…，θn（cn－1））∈C，

进而有（θn＋1（cn－1），θn＋1（c0），…，θn＋1（cn－2））∈C，又因 为n 为奇 数 且θ2＝1，所以 （cn－1，c0，…，cn－2）∈C，故C是R上长度为n的循环码。

3 环R上斜循环码的对偶码

定义3 设x＝（x1，x2，…，xn），y＝（y1，y2，…，yn）为Rn中的2个元素。x与y的欧几里得内积定义为：

〈x，y〉＝x1y1＋x2y2＋…＋xnyn，x与y的厄米特内积定义为：

［x，y］＝x1θ（y1）＋x2θ（y2）＋ … ＋xnθ（yn）。

定义4 设码C是R上长度为n的线性码，码C在欧几里得内积下的对偶码为：

C⊥＝｛x∈Rn｜〈x，c〉＝0，∀c∈C｝。码C在厄米特内积下的对偶码为：

C＊＝ ｛x∈Rn｜［x，c］＝0，∀c∈C｝。若C⊥＝C，则称码C为欧几里得自对偶码；若C＊＝C，则称码C为厄米特自对偶码。

定理7 设码C是R上长度n的斜循环码，则C⊥和C＊也为斜循环码。

证明 对∀c＝（c0，c1，…，cn－1）∈C⊥，a＝（a0，a1，…，an－1）∈C，有〈c，a〉＝0。若n为偶数，由斜循环码的定义知：

（θn－1（a1），θn－1（a2），…，θn－1（a0））∈C，c0θn－1（a1）＋c1θn－1（a2）＋…＋cn－1θn－1（a0）＝0，

即有θ（c0）θn（a1）＋θ（c1）θn（a2）＋ … ＋θ（cn－1）θn（a0）＝0。因为n为偶数，则有：

θ（cn－1）a0＋θ（c0）a1＋θ（c1）a2＋ …

＋θ（cn－2）an－1＝0，

（θ（cn－1），θ（c0），…，θ（cn－2））∈C⊥，所以C⊥为斜循环码。

若n 为奇数，可知（θn－1（a1），θn－1（a2），…，θn－1（a0））＝（a1，a2，…，a0）∈C，则a1c0＋a2c1＋…＋a0cn－1＝0，即（cn－1，c0，…，cn－2）∈C⊥，由于

（θn（a0），θn（a1），…，θn（an－1））＝（θ（a0），θ（a1），…，θ（an－1））∈C，

cn－1θ（a0）＋c0θ（a1）＋ … ＋cn－2θ（an－1）＝0，即a0θ（cn－1）＋…＋an－1θ（cn－2）＝0，所以有：（θ（cn－1），θ（c0），…，θ（cn－2））∈C⊥。同理可证C＊也为斜循环码。

引理2 如果n为偶数，且xn－1＝h（x）＊g（x），其中g（x）、h（x）为R［x；θ］中首一的多项式，码C＝（g（x））是Rn中的斜循环码，那么对于任意的c∈C，当且仅当在Rn中c（x）＊h（x）＝0。

证明 当c∈C时存在p（x）∈Rn使c（x）＝p（x）＊g（x）。由推论2知，在Rn中有：

c（x）＊h（x）＝ （p（x）＊g（x））＊h（x）＝

p（x）＊（h（x）＊g（x））＝0。

反之若在Rn中c（x）＊h（x）＝0，则

c（x）＊h（x）＝p（x）＊（xn－1）＝p（x）＊（h（x）＊g（x））＝（p（x）＊g（x））＊h（x），

又因为h（x）不为零因子，所以有c（x）＝p（x）＊g（x）∈C。

定理8 设C＝（g（x））为R上偶长度n、维数为k的斜循环码。假设xn－1＝h（x）＊g（x），其中g（x）＝g0＋g1x＋…＋gn－k－1xn－k－1＋xn－k，h（x）＝h0＋h1x＋…＋hk－1xk－1＋xk，则其对偶码C⊥＝（h（x）），h（x）＝θk（h0）xk＋θk－1（h1）xk－1＋…＋1。

证明 由 引理2知，对 ∀c＝ （c0，c1，…，cn－1）∈C，f（x）＝c（x）＊h（x）＝0。所以f（x）中xs（1≤s≤n－1）项的系数为0，即其中，hk＝1；ht＝0；k＋1≤t≤n－1。

令β＝（hs，θ（hs），…，θs（h0），θs＋1（hn－1），…，θn－1（hs－1）），那么〈c，β〉＝0，且c与β 及其所有的循环移位欧几里得正交，所以（h（x））⊆C⊥。

若k 为 奇 数，令g（x）＝1＋gn－k－1x ＋θ（gn－k－2）x2＋…＋θ（g1）xn－k－1＋g0xn－k。

若k为偶数，令g（x）＝1＋θ（gn－k－1）x＋gn－k－2x2＋…＋θ（g1）xn－k－1＋g0xn－k。

由于h（x）＊g（x）＝xn－1，在Rn中g（x）＊h（x）＝0，所以h（x）为xn－1的右因式。又｜（h（x））｜＝｜R｜n－k＝｜C⊥｜，故C⊥＝（h（x））。

定理9 设xn－1＝h（x）＊g（x），其中h（x）、g（x）为首一的多项式。C＝（g（x））为R上偶长度n、维数为k的斜循环码，则

证明 与定理8的证明类似。

推论3 若环R上的斜循环码为欧几里得自对偶码，那么该循环码的常数项系数和长度要满足：①g0＝1＋2v或3＋2v；②n＝2k，其中k为奇数。

证明 设码C＝（g（x））是环R上长度为n的斜循环自对偶码，其中，

g（x）＝g0＋g1x＋…＋gk－1xk－1＋xk，g0≠0。易知n＝2k，由定理8知（h（x））＝（g（x）），那么g0为单位，且

又因为在R［x；θ］中h（x）＊g（x）＝xn－1，故θk（g0）＝－g0，所以g0＝1＋2v或3＋2v，k为奇数。由此得n＝4，8，12时没有斜循环自对偶码，进一步得n＝2，6，10时也没有斜循环自对偶码，所以当n≤12时环R上没有斜循环自对偶码。

4 结束语

本文给出了环Z4＋vZ4上的自同构，讨论了该环上斜循环码C的生成多项式，进一步证明了偶长度的斜循环码等价于指数为2的准循环码，奇长度的斜循环码等价于循环码。并给出了在欧几里得内积和厄米特内积下环R上偶长度斜循环码的对偶码的生成多项式。由于Z4＋vZ4上斜循环码是广义的循环码，其个数比循环码要多，从而通过斜循环码有利于得出一些性质好的码。

［1］ Hammons A R，Kumar P V，Calderbank A R，et al.The linearity of Kerdock，Preparata，Goethals，and related codes［J］.IEEE Trans Inform Theory，1994，40（2）：301－319.

［2］ Boucher D，Geiselmann W，Ulmer F.Skew cyclic code［J］.Applied Algebra in Engineering，Communication and Computing，2007，18（4）：379－389.

［3］ Boucher D，Ulmer F.Coding with skew polynomial rings［J］.Journal of Symbolic Computation，2009，44（12）：1644－1656.

［4］ Abualrub T，Ghrayeb A，Aydin N，et al.On the construction of skew quasi－cyclic codes［J］.IEEE Trans Inform Theory，2012，56（5）：2081－2090.

［5］ Boucher D，Sole P，Ulmer F.Skew constacyclic codes over Galois rings［J］.Advances in Mathematics of Communications，2008，2（3）：273－292.

［6］ Jitman S，Ling S，Udomkavanich P.Skew constacyclic codes over finite chain rings［J］.Advances in Mathematics of Communications，2012，6（1）：29－63.

［7］ Boucher D，Ulmer F.Codes as modules over skew polynomial rings［J］.Lecture Notes in Computer Science，2009，5921：38－55.

［8］ Abualrub T，Aydin N，Seneviratne P.Onθ－cyclic codes over F2＋vF2［J］.Australasian Journal of Combinatorics，2012，54：115－126.

［9］ 徐贤奇，朱士信.环F4＋vF4上的斜循环码［J］.合肥工业大学学报：自然科学版，2011，34（9）：1429－1432.

［10］ Gao J.Skew cyclic codes over Fp＋vFp［J］.Journal of Applied Mathematics and Informatics，2013，31 （3／4）：337－342.

［11］ Bandi R K，Bhaintwal M.Codes over Z4＋vZ4with repect to Rosenbloom－Tsfasman metric［C］／／Advances in Computing，Communications and Informatics （ICACCI），2013 International Conference on.IEEE，2013：37－41.

［12］ Zhu S，Wang Y，Shi M.Some results on cyclic codesover F2＋vF2［J］.IEEE Trans Inform Theory，2010，56（4）：1680－1684.