缺陷对一维尘埃等离子体晶格色散关系的影响

黄雪梅， 王春华， 孙晓霞， 胡乐佳

（合肥工业大学 电子科学与应用物理学院，安徽 合肥 230009）

0 引 言

尘埃等离子体晶格研究自从在实验室中发现以来便得到了飞速的发展，除了等离子体物理自身研究的需要，还为凝聚态物理等学科的研究提供了非常好的“宏观”模型，如利用等离子体晶格来研究固体中的相变过程［1］。对于周期条件下的连续介质，如果存在不同的独立的周期模式，则2个周期模式的频率（能量）连续谱会在相交处线性耦合并产生能隙［2］。而由于杂质或缺陷等因素的存在则有可能在能隙中形成分立谱的本征模，如凝聚态物理中的隙模［3］和托卡马克等离子体中的环形阿尔芬本征模（TAE模）［4］。文献［5］通过磁场中尘埃晶格本身周期性以及回旋周期性得到了尘埃等离子体晶格中类似的能隙结构。为进一步深入研究等离子体晶格性质以及为凝聚态材料掺杂及缺陷性质的研究提供物理模型，本文采用一维尘埃等离子体晶格模型，通过引入杂质粒子，研究其中波传播的色散关系，进而分析缺陷对能级结构的影响。

1 模型的建立和色散关系的推导

一维尘埃等离子体晶格模型如图1所示。

图1中，由质量为m1、电量为Q1的尘埃粒子构成沿x方向的一维无限长尘埃等离子体晶格链，粒子平衡位置之间的距离为Δ，原点右边第1个位置的粒子被质量为m2、电量为Q2的缺陷尘埃粒子所取代。

图1 一维尘埃等离子体晶格模型

忽略尘埃粒子尺寸大小的影响，将其看作带负电的点电荷，并设：

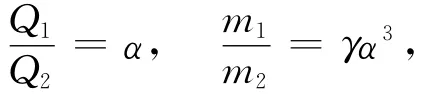
其中，α和γ为可变参数［6］。

已知等离子体中带电量为Q的粒子产生的电势为库仑屏蔽势［7］，即

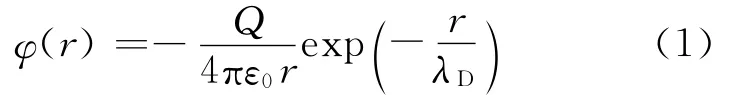
其中，λD为 德 拜 长 度；r＝ ［（x－x0）2＋ （yy0）2＋，为场点（x，y，z）与源点（x0，y0，z0）的距离。则在晶格链中，位于（x0，0，0）处的粒子满足的运动方程为：

其中，r′＝ξi＋ηj＋ζk为粒子离开其平衡位置的线性化位移，粒子总的位移为r＝（x0i＋r′）＝（x0＋ξ）i＋ηj＋ζk。

（2）式右边第1项为粒子受到的静电场力，E

＝－2φ，为所有带电粒子产生的电势之和；Fconf＝－2φconf，为鞘层对粒子的y方向上的约束力，其中，Ωy为粒子在y方向约束力作用下的共振频率［8］。

本文采用文献［9］给出的求解等离子体晶格波色散关系的方法，只考虑xy平面内传播的波，可设（ξ，η）＝（ξ0，η0）exp（ikx－iωt），对原有粒子和缺陷粒子都满足的（2）式进行线性化和傅立叶变换，并作如下归一化处理：

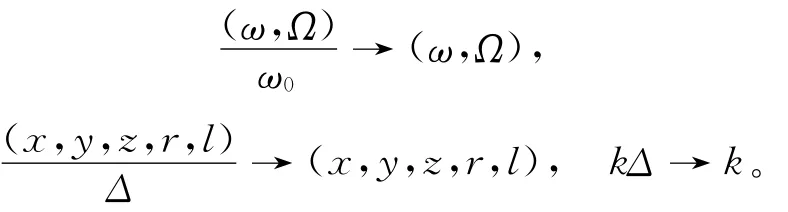
得到其中晶格纵波色散关系表达式为：

其中

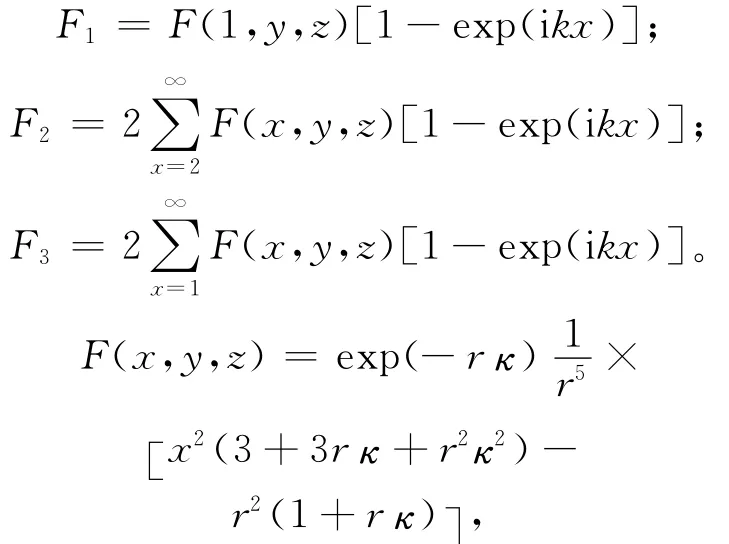
其中，κ＝Δ／λD为粒子间距与德拜长度之比。

对于横波，要考虑到y方向上鞘层对粒子的约束力Fconf。得到横波的色散关系为：

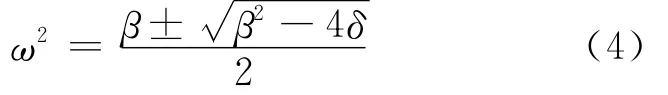
其中

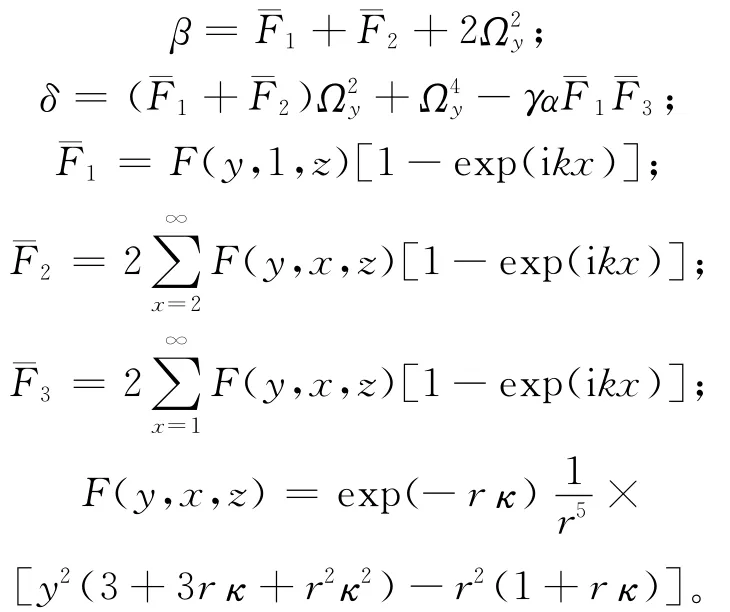
2 讨 论

采用实验室中可以测量的量，如无量纲化的κ＝0.84，尘埃粒子电量Q1＝759 5e，质量m1＝2.62×1014mp，mp为1个质子的质量，尘埃粒子间距Δ＝7.2×10－4m，以及由此得到的ω0＝Q1／（m1Δ3）1／2＝8.0s－1和共振频率Ωy＝2.63Hz。

一维尘埃等离子体晶格链中晶格波的色散关系如图2所示。

在上述尘埃粒子模型中，当参数α＝1，γ＝1时，可以得到单一尘埃粒子链色散关系，如图2a所示，此结果与以前的理论［10－11］相符合。

当α≠1，γ＝1时，即原点右边第1个位置的粒子被另一个与其不同电量和质量的缺陷粒子所取代，由图2b可以看出，当α＞1时，即晶格缺陷为带电量和质量均较小的带电粒子时，无能隙产生。而当α＜1时，即晶格缺陷为1个带电量和质量均较大的带电粒子时，则出现能隙结构如图2c，且随着α的减小，能隙增大，如图2d所示。

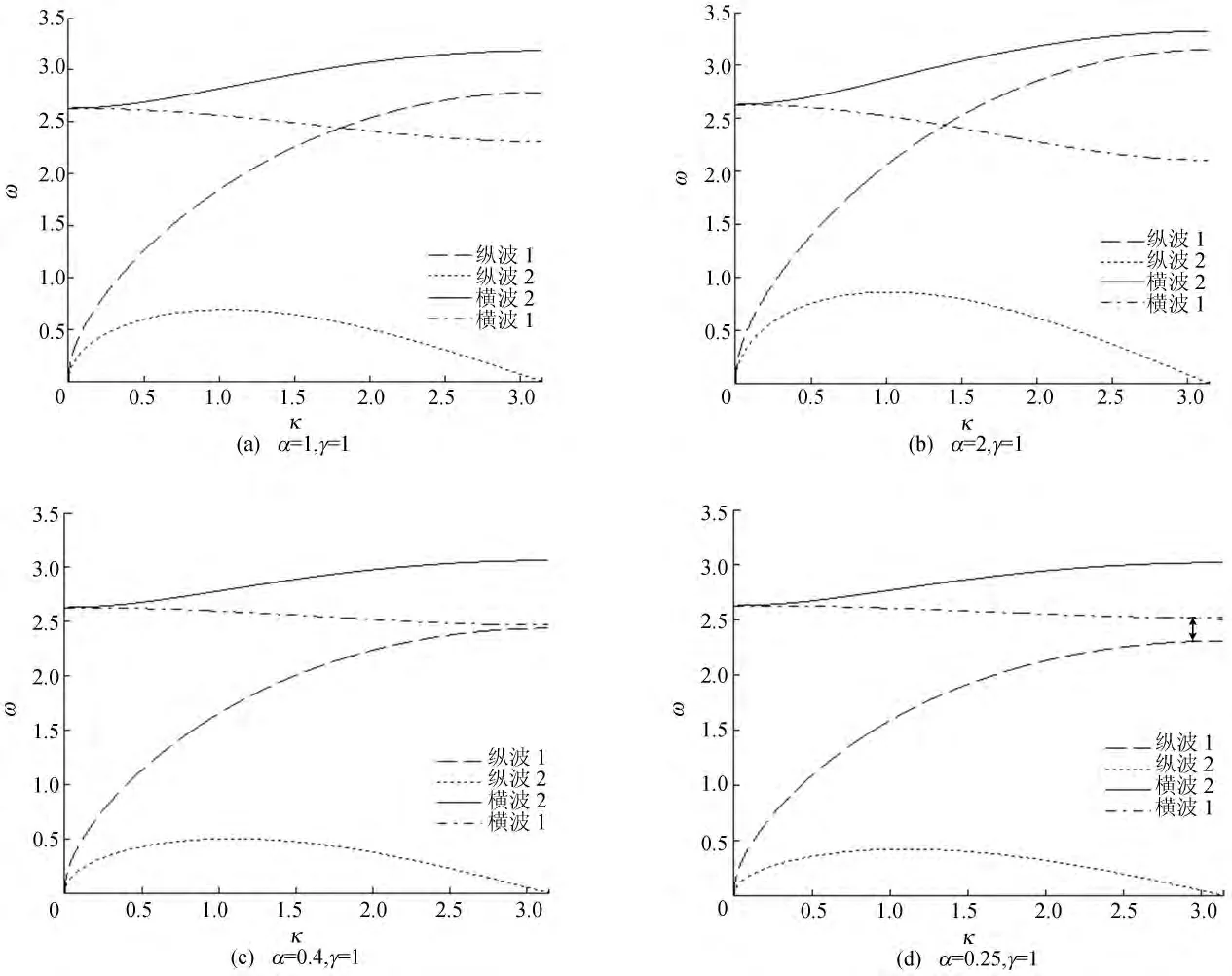
图2 一维尘埃等离子体晶格链中晶格波的色散关系图

3 结束语

本文采用库仑屏蔽作用势，当一维无限长尘埃等离子体晶格中存在单个晶格缺陷时，对其中传播的横波和纵波的色散关系进行推导和分析，进而研究其中的能隙结构。研究发现当缺陷粒子的电量和质量比原有带电粒子大时会出现能隙，即当原有晶格链的周期性被破坏时，会出现能隙结构。

［1］ Thomas H，Morfill G.Melting dynamics of a plasma crystal［J］.Nature，1996，379：806－809.

［2］ 孙晓霞，王春华.碳纳米管中晶格波的研究［J］.合肥工业大学学报：自然科学版，2010，33（7）：1086－1089.

［3］ Kittel C.Introduction to solid state physics［M］.8th ed.John Wiley ＆ Sons，Inc，2004：104－108.

［4］ Cheng C Z，Chen L，Chance M S.Highk－n ideal and resistive shear Alfvén waves in tokamaks ［J］.Annal Phys，1985，161：21－47.

［5］ Sun X，Wang C，Wang X.Dust lattice waves of dusty plasma chain with an external magnetic field［J］.Chin Phys Lett，2007，24：771－773.

［6］ 崔利娟.一维尘埃晶格链中的能隙及杂质能级［D］.大连：大连理工大学，2007.

［7］ Konopka U，Morfill G E，Ratke L.Measurement of the interaction potential of microspheres in the sheath of a rf discharge［J］.Phys Rev Lett，2000，84（5）：891－894.

［8］ Lvlev A V，Morfill G.Anisotropic dust lattice modes［J］.Phys Rev E，2000，63（1）：016409.

［9］ Wang X，Bhattaeharjee A，Hu S.Longitudinal and transverse waves in Yukawa crystals［J］.Phys Rev Lett，2001，86（12）：2569－2572.

［10］ Liu B，Avinash K，Goree J.Transverse optical mode in a one－dimensional Yukawa chain［J］.Phys Rev Lett，2003，91（25）：255003.

［11］ Liu B，Avinash K，Goree J.Characterizing potentials using the structure of a one－dimensional chain demonstrated using a dusty plasma crystal［J］.Phys Rev E，2004，69：036410.