基于三坐标测量的螺旋锥齿轮检测关键技术

武冠宏， 赵 韩， 吴占雨， 余 晗

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

随着国内外三坐标测量机的迅速发展，三坐标检测技术已经成为检测齿轮精度的重要手段［1］。三坐标测量主要实现方法是在计量级三坐标测量机或齿轮测量机上，按照预定的遍布全齿面的网格测量网格结点处的齿面坐标，再通过适当的软件处理，得到网格结点处的法向偏差，进而求得差曲面的几何参数，并运用误差相关性识别技术，求得最佳切齿修正方案［2－3］。

螺旋锥齿轮传动啮合齿面之间的接触方式为空间点接触，在考虑啮合过程中齿面弹性变形的情况下，两齿面间的接触是以接触点为中心形成的一个椭圆形接触区［4］。且传动效率与两齿面间的接触轨迹有直接关系，为了使齿面的动静态性能良好，实际生产时螺旋锥齿轮齿面以经过理论优化的齿面为目标齿面，这样可以在实际生产中重复制造出经过几何精度控制技术和实践检验而设计出的齿面。因此，基于三坐标测量机的齿面几何精度控制技术和齿面接触分析已成为现代螺旋锥齿轮加工精度技术的发展趋势，未来的应用会更加广泛。

1 基于啮合原理的齿面方程理论

建立螺旋锥齿轮的齿面数学模型是三坐标测量的基础，在此基础上，齿面几何建模、齿面网格测量点计算以及真实齿面建模等步骤可以有章可循，为研究真实齿面接触分析、断裂分析和建立调整机床加工参数与齿面误差之间的方程提供了必要准备。

小轮加工中使用了刀倾机构，因此在具体处理时会复杂得多，为了不失一般性，本文只建立左旋小轮的齿面模型。首先建立小轮的加工坐标系如图1所示，其中，Sm1＝｛om1：xm1ym1zm1｝，Sq＝｛oq：xqyqzq｝，为机床和工件坐 标系并 与床身固连。Sc＝｛oc：xcyczc｝、S1＝｛o1：x1y1z1｝分别为与摇台、齿轮固连的可运动坐标系；St1＝｛ot1：xt1yt1zt1｝为与刀具固连的坐标系；Sb＝｛ob：xbybzb｝为刀具刀倾刀转前与摇台固连的坐标系；Sn＝｛on：xnynzn｝为辅助坐标系并与机床固连［5］。

图1 机床与刀具关系

由文献［6］可知齿面方程建立所需参数。小轮刀盘圆锥面方程可表示为：

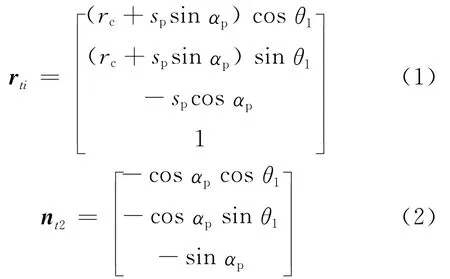
其中，rc为刀尖半径；α为刀具齿形角，αp＝－α；sp为刀刃与轮坯啮合点到刀顶的距离。

刀盘坐标系St1到固连于摇台的坐标系Sc的坐标变换为：

固连于摇台的坐标系Sc到固连于机床的坐标系Sm1的坐标变换为：

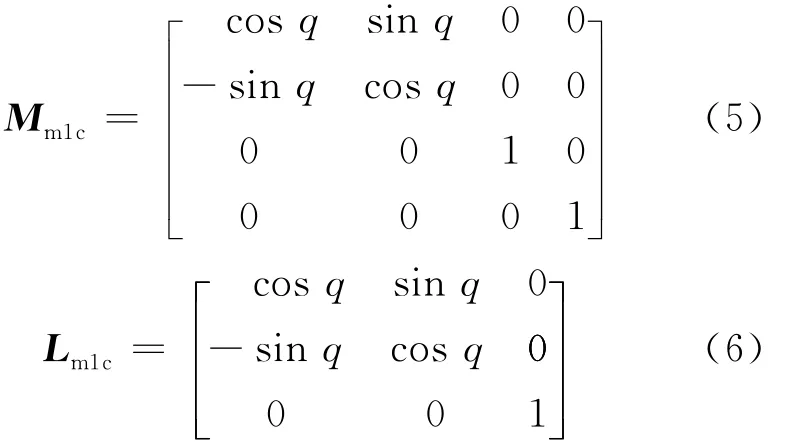
固连于机床的坐标系Sm1到工件坐标系S1的坐标变换为：

以切削面为第1曲面，小轮为第2曲面，设小轮在坐标系Sm1下的角速度为：

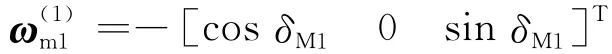
则小轮加工时产形轮在坐标系Sm1下的角速度为，令

根据齿轮啮合原理有：

则啮合方程可表示为：

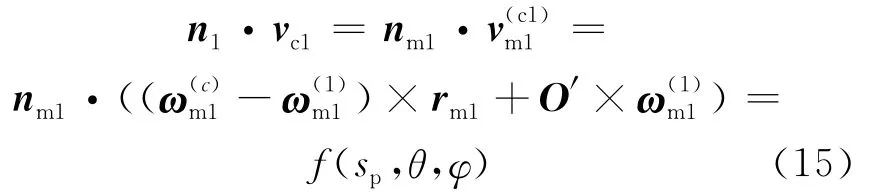
将（15）式写成sp的表达式，小轮齿面方程在齿轮坐标系S1中可简写成曲面坐标函数的形式：

2 齿面网格划分、节点测量及误差修正

螺旋锥齿轮的齿面是复杂空间曲面，为了最大范围取得齿轮啮合范围的测量点，一般将齿面旋转投影到轴截面上形成拓扑图，选取平面映像与齿面点一一对应均匀的点。

在螺旋锥齿轮齿面的投影边界被确定以后，就可以进行网格划分，采用螺旋锥齿轮测量的相关标准，求得旋转投影面上的网格节点函数后，将投影面上的节点坐标转换到齿面上，实现真实齿面数字化表达。最后，设曲面上任一网格节点处到齿轮轴线的距离为S＝nr（θ，u），通过迭代和坐标变换即可求出节点坐标值。

三坐标测量步骤如下：

（1）齿轮定位，保证被测齿轮中心与转台中心重合。

（2）确定基准，建立坐标系。三坐标测头在齿轮基准面上取点以确定基准面在三坐标测量机中的位置，进而可以确定齿轮在坐标测量机中的位置，然后建立齿轮坐标系。

（3）选取测针。测针的选择原则是被测点的切平面与过该点的端平面的交线与测针的夹角必须大于0［7］，所以对于节锥角大的大轮，一般采用一根垂直测针来完成，节锥角小的齿轮则采用水平测针来完成。但利用点测量方法在描述真实齿面的过程中，精确度往往会降低，对误差的合成产生影响。

以机载格里森螺旋锥齿轮为例，齿轮模数为3.5，螺旋角为14°07′47″，压力角为20°00′00′，齿数为62。根据齿轮参数计算待测网格节点的三坐标值并把各节点坐标值存入数据库中，为减少随机误差，一般选取齿轮的4个齿进行测量［8］；根据文献［9］方法可知，该齿轮测量选用5×9的网格节点。因为网格过密则可能把测量误差带入测量结果，网格过疏又不能很好反映齿轮的齿面形状，所以一般都取5×9的网格。最后，将三坐标测量机依次测量各个节点的实际坐标值存入数据库中。至此，完成对1个齿的测量，另外3个齿的测量方法与之相同。

根据上述测量的齿面误差数据计算出齿面误差，通过改变刀具与轮坯的相对位置和相对速度调整机床参数使之满足误差平方和最小［10］。因此，理论齿面方程可以理解为各个调整参数的函数，本文使用敏感系数矩阵作为测量网格点的法向误差的主要参数。

机床参数调整引起微小变化的齿面法向误差的叠加称为齿面法向误差［11］，即

其中，Δu为理论齿面i点的法向误差值；Δξj为第j项机床调整参数的微小变化；λij为齿面i点误差随第j项机床调整参数变化的敏感系数，各敏感系数可以通过对各项机床调整参数求偏导和点乘对应点的法矢得到，即λij＝（∂ui／∂ξj）·ni。选取实例中理论齿面上取的点，分别求取各点法向误差随机床调整参数变化的敏感系数，建立敏感系数矩阵，则全齿面上点的法向总误差为：

其中，λij为齿面点随机床调整参数变化的敏感系数矩阵。

根据总误差的敏感系数矩阵，调整（18）式中参数，即可进行对齿面误差的修正。

3 实验验证

为验证上述理论，对某型无人机主减速器的格里森螺旋锥齿轮进行三坐标检测，并与普通齿轮测量仪检测的结果进行对比。齿轮实物如图2所示。参数如前所述。

图2 实验用螺旋锥齿轮

实验结果见表1、表2所列，如图3、图4所示。表中，Fa为齿廓总偏差；ffa为齿廓形状偏差；fHa为齿廓斜率偏差；Ca为齿廓凸度。

表1 齿轮测量仪测量数据

从实验结果可知，基于三坐标检测的轮廓总偏差值和齿距累计总误差值要远小于普通齿轮检测仪，避免了由误差造成的测量精度不准的问题，因此可将此类数据应用于齿面修正和机床加工参数修正，提高螺旋锥齿轮加工精度。

表2 三坐标测量仪测量数据

图3 普通齿轮测量仪检测结果

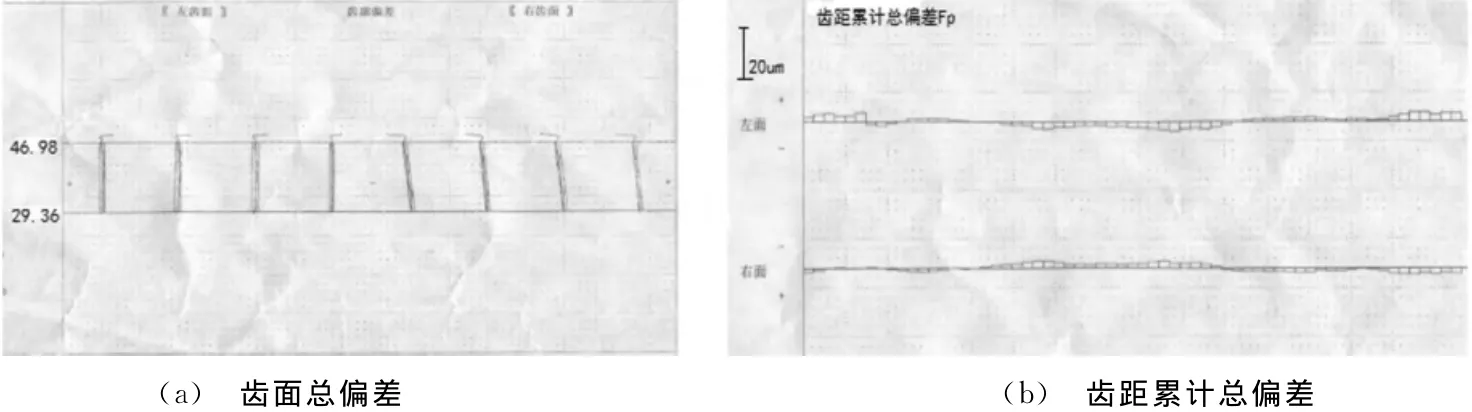
图4 三坐标检测结果

4 结束语

本文根据基本啮合原理建立了理想螺旋锥齿轮齿面方程，并划分了测量网格，利用三坐标测量机成功进行螺旋锥齿轮参数的测量，验证了齿面方程的正确性，并做了对比实验。结果表明：三坐标检测具有较小的齿面轮廓偏差、齿距累计误差和较高的测量精度，提高了测量准确性，并可以将测量数据应用于真实齿面方程的改进，对机床加工参数修正有一定参考价值，对提高螺旋锥齿轮的齿面精度控制有积极作用。

［1］ 刘祚时，倪潇娟.三坐标测量机（CMM）的现状和发展趋势［J］.机械制造，2004，42（48）：33－35.

［2］ 王 军，王小椿，姜 虹，等.螺旋锥齿轮齿面的三坐标测量［J］.机械工程学报，2003，39（6）：151－155.

［3］ 聂恒敬.齿轮检测设备误差修正研究 ［J］.合肥工业大学学报：自然科学版，1993，26（Z1）：10－14.

［4］ 沈小星，周云飞，李左章，等.螺旋锥齿轮点接触齿面生成法［J］.中国机械工程，1999，16（7）：45－48.

［5］ 梁 艳.三维坐标测量机实现螺旋锥齿轮测量的研究［J］.科技信息，2009（19）：465－466.

［6］ 邢 彬.螺旋锥齿轮齿面三坐标测量机测量关键技术与测量数据应用研究［D］.长沙：中南大学，2010.

［7］ 梁 艳，张 琳，李仕春，等.弧齿锥齿轮齿面坐标法测量的研究［J］.工具技术，2006（40）：120－123.

［8］ 余晓芬，费业泰.齿形误差测量最佳被测齿面的确定［J］.合肥工业大学学报：自然科学版，1993，26（Z1）：23－26.

［9］ 吕罕聪.螺旋锥齿轮测量方法研究［D］.西安：西安理工大学，2007.

［10］ 苏进展，方宗德，谷建功.螺旋锥齿轮齿面误差修正［J］.农业机械学报，2010，41（3）：200－204.

［11］ 唐进元，邢 彬.基于三坐标测量机的螺旋锥齿轮加工参数反 调 修 正 ［J］.北 京 工 业 大 学 学 报，2010，36（11）：1451－1456.