四步八阶迭代法解非线性方程组

朱小飞， 檀结庆， 张 旭

（合肥工业大学 数学学院，安徽 合肥 230009）

非线性方程和非线性方程组的数值解法［1－3］是计算数学的一个重要的研究内容，它在解决很多实际问题中起到了重要作用。Newton迭代方法是最经典的迭代方法，具有二阶收敛性。Halley迭代法和Chebyshev迭代法是三阶收敛的，文献［4－5］利用Adomian分解法分别给出了三阶收敛和四阶收敛的迭代方法，文献［6－7］根据求积公式分别提出了具有四阶收敛和五阶收敛的迭代方法。

1 迭代方法

考虑非线性方程组F（x）＝0，其中函数F（x）：D⊂Rn在凸集D⊂Rn上p阶可微，且ξ是非线性方程组的一个实数根，对函数F（x）进行Taylor展开［8］得：

当p＝1时，可得：

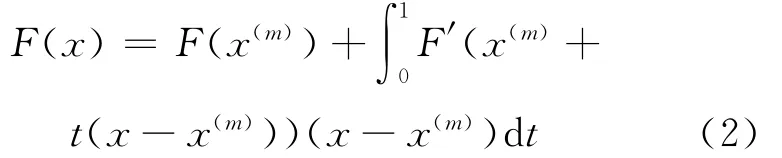
利用左矩形积分公式可得：

将（3）式带入（2）式，并令F（x）＝0得：

进而得到如下迭代格式：

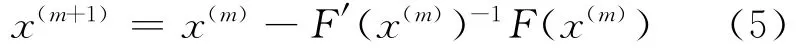
（5）式为经典的Newton迭代格式。对于（2）式中的积分部分，若利用不同的数值积分公式则可以得到不同的迭代方法。文献［9］提出了2点Newton－Cotes公式，即闭－开求积公式和开－闭求积公式：

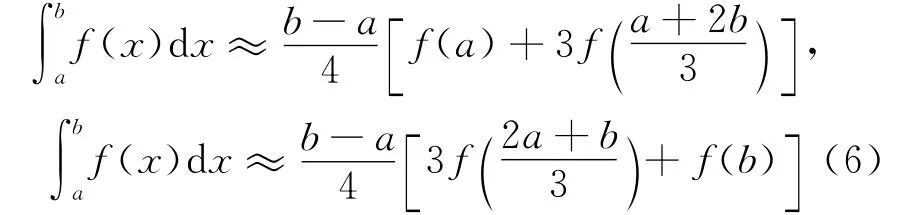
文献［10］利用（6）式的2种积分公式来近似（2）式中的积分部分，得到：

相应地得到了2种改进的两步求解非线性方程组的迭代方法，即

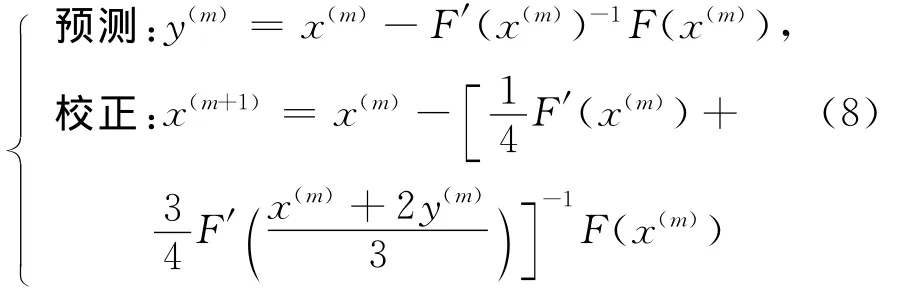
文献［11］给出了1种改进的求解非线性方程组的迭代方法，即

文献［12］给出了1种改进的求解非线性方程组的两步Newton迭代方法，即

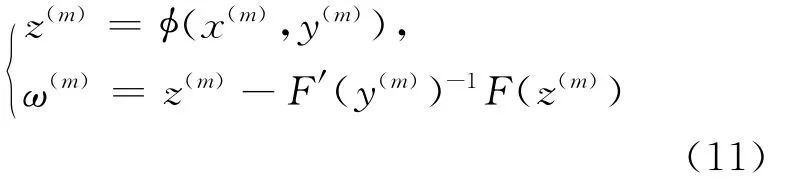
其中，y（m）＝x（m）－F′（x（m））－1F（x（m））为著名的二阶收敛的Newton迭代方法。

文献［7］根据以上公式得到了相应的3种求解非线性方程组的迭代方法，并证明其是一阶收敛的，即

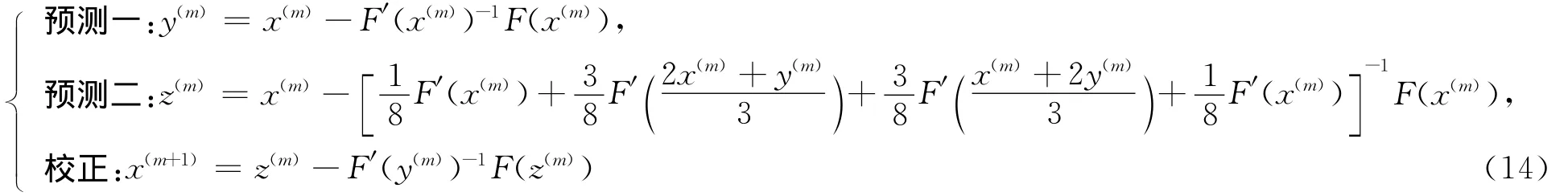
本文在上述三步五阶迭代方法的基础上再加一步，得到了相应的3种新的求解非线性方程组的迭代方法，并证明其是五阶收敛的。（1）新方法一。

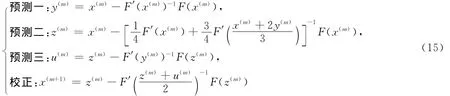
（2）新方法二。

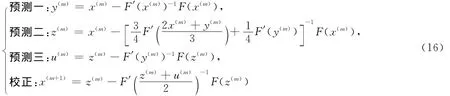
（3）新方法三。

（8）～（17）式中m＝0，1，2，…。

2 收敛分析

定理1 设F（x）：D⊂Rn→Rn在凸集D 上p阶可微，且非线性方程组F（x）＝0在凸集D上存在根η，则上面提出的3种迭代方法（15）～（17）式都是八阶收敛的，且满足误差等式：

其中

证明 先证明方法一，即（15）式具有八阶收敛。分别将F（x（m））、F′（x（m））、F′（y（m））在点η处运用Taylor公式展开得：

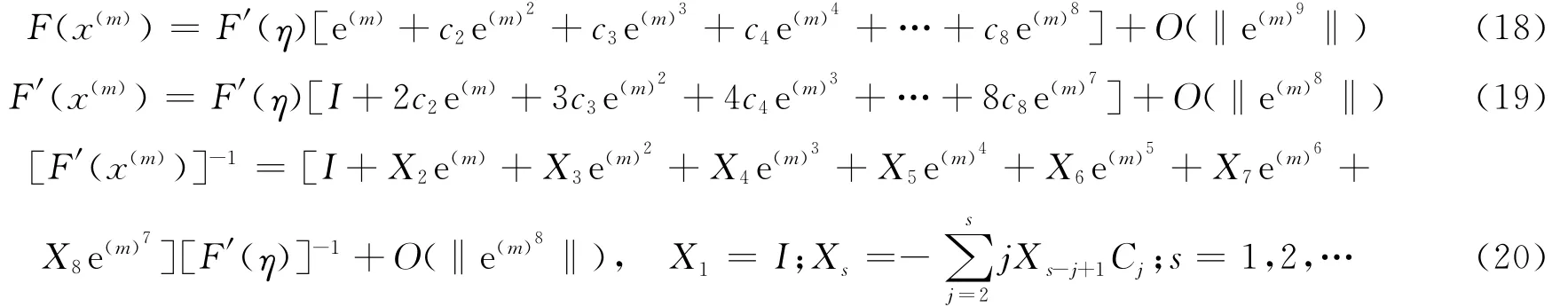
由（18）式和（15）式的预测一可得：

由（21）式可得：

其中，

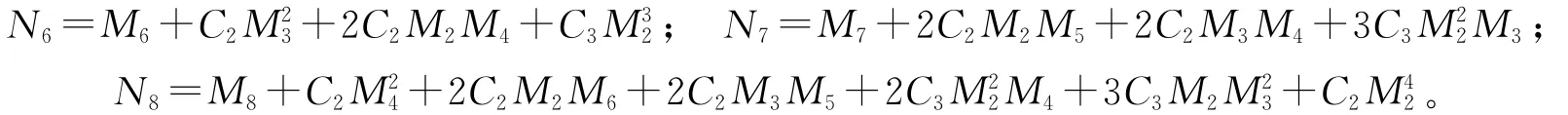
由（22）式可得：

其中，

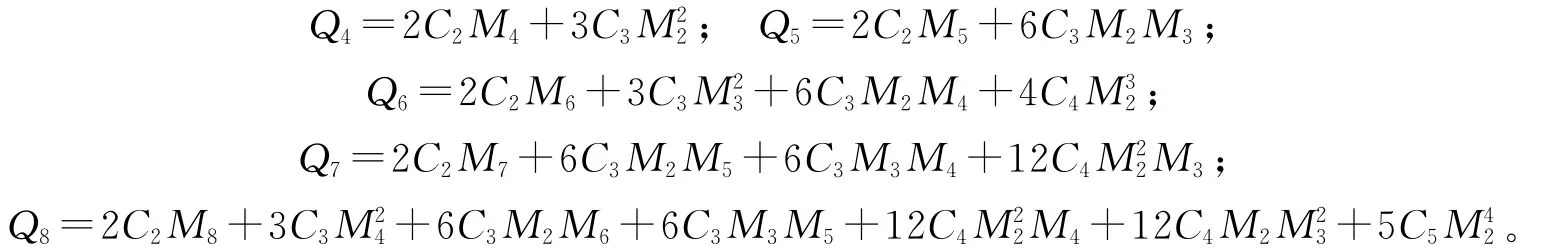
因为［7］

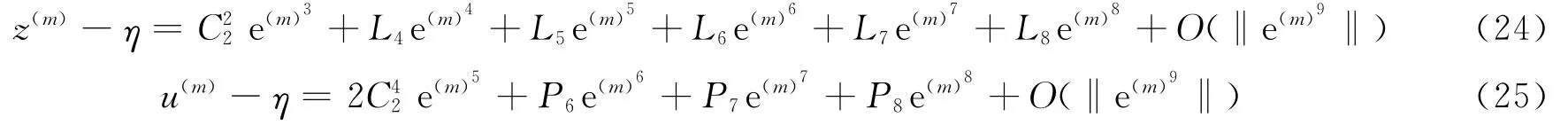
所以［7］

其中，R5＝L5／2＋C42；R6＝L6／2＋P6／2；R7＝L7／2＋P7／2；R8＝L8／2＋P8／2。

所以有：

其中，

T6＝2C2R6＋34C3C42； T7＝2C2R7＋32C22C3L4； T8＝2C2R8＋34C3L24＋3C22C3C5。

由（24）式可得：

综上可得：

即证得新方法一（15）式具有八阶收敛，同样可证得新方法二、新方法三都具有八阶收敛。

3 数值实例

分别用牛顿迭代公式（Newton）、文献［7］提出的算法（方法一和方法三）以及本文提出的3种新方法（取其中的新方法一和新方法三）求解几个非线性方程组，并比较这些不同的方法在每次迭代后得到的近似解。所有的结果都是在Matlab R2010b环境下实现的。

例1 解非线性方程组：

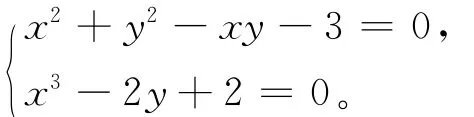
取初始值为［2.5，5］T，数值计算结果见表1所列。

例2 解非线性方程组：

取初始值为［0.5，2，3］T，数值计算结果见表2所列。

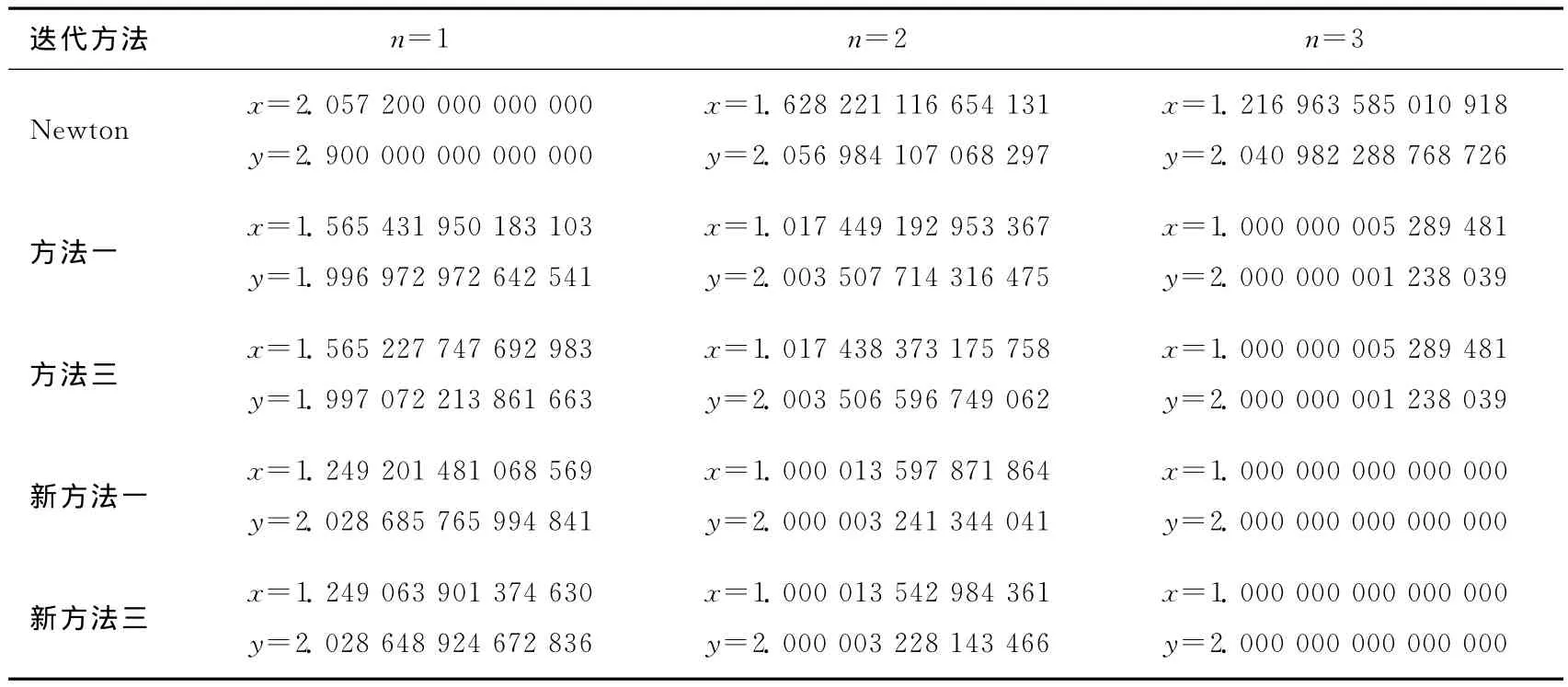
表1 例1不同方法迭代3次后的计算结果

表2 例2不同方法迭代3次后的计算结果

以上数值实例表明，本文提出的3种求解非线性方程组的方法都是可行的，且所需的迭代次数较少，收敛速度较快。

效率指数如图1所示，由图1可以得到，当迭代次数n＜3.5时，本文的方法效果相对较好。

4 结束语

本文给出了3种新的解非线性方程组的方法，并证明其具有八阶收敛性；数值实例表明这3种方法都是可行的，且本文方法迭代的次数较少，收敛速度较快，本文方法效率指数也相对较好。

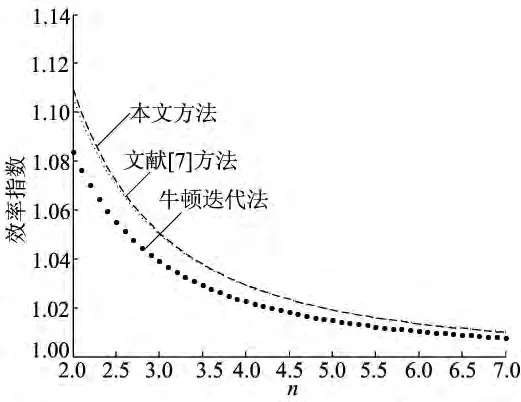
图1 效率指数图

［1］ 李庆扬，莫孜中，祁力群，等.非线性方程组的数值解法［M］.北京：科学出版社，1987：25－108.

［2］ 同济大学计算数学教研室.现代数值计算［M］.北京：人民邮电出版社，2009：10－90.

［3］ 陈小惠，唐 烁.解非线性方程的一类多参数迭代格式［J］.合肥工业大学学报：自然科学版，2011，34（2）：309－312.

［4］ Darvishi M T，Barati A.Super cubic iterative methods to solve systems of nonlinear equations［J］.Applied Mathematics and Computation，2007，188（2）：1678－1685.

［5］ Babajee D K R，Dauhoo M Z，Darvishi M T，BaratiA.A note on the local convergence of iterative methods based on Adomian decomposition method and 3－node quadrature rule［J］.Applied Mathematics and Computation，2008，200（1）：452－458.

［6］ 代璐璐，檀结庆.两种解非线性方程组的四阶迭代方法［J］.数值计算与计算机应用，2012，33（2）：121－128.

［7］ 张 旭，檀结庆.三步五阶迭代方法解非线性方程组［J］.计算数学，2013，35（3）：297－304.

［8］ Ortega J M，Rheinboldt W C.Iterative solution of nonlinear equations in several variables［M］.New York and London：Academic Press，1970：30－268.

［9］ Podisuk M，Chundang U，Sanprasert W.Single step formulas and multi－step formulas of the integration method for solving the initial value problem of ordinary differential equation［J］.Applied Mathematics and Computation，2007，190（2）：1438－1444.

［10］ Noor M A，Waseem M.Some iterative methods for solving a system of nonlinear equations［J］.Computers and Mathematics with Applications，2009，57（1）：101－106.

［11］ Khirallah M Q，Hafiz M A.Novel three order methods for solving a system of nonlinear equations［J］.Bulletin of Society for Mathematical Services and Standards，2012，1（2）：1－14.

［12］ Cordero A，Hueso J L，Martinez E，Torregrosa J R.Increasing the convergence order of an iterative method for nonlinear systems ［J］.Applied Mathematics Letters，2012，25（12）：2369－2374.