基于嵌套树模型检测的研究

郭 婧， 徐中伟， 李丽梅

（1.同济大学 电子与信息工程学院，上海 201804；2.九江学院 图书馆，江西 九江 332005）

随着计算机技术的快速发展，人们对计算机软件安全的要求不断提高。模型检测作为软件安全检测的重要工具被广泛应用。模型检测［1］是软件自动验证技术，它是将要验证的系统用变迁系统来表示，通过验证来观察该系统是否满足需求。符号模型检测［2］的出现使模型检测得到更大的发展，可以将状态集合用布尔函数来表示［3］。用有序二叉决策图（ordered binary decision diagram，OBDD）来处理布尔函数，再通过优化方法又可以处理更多的状态数，使符号模型检测能更好地投入实际应用中［4］。OBDD仍无法避免状态爆炸的问题，无论变量顺序如何，需要的存储空间都是指数增长的［5］。因此，可满足性问题（satisifiability problem，SAT）工具［6］得到广泛应用。限界模型检测能解决OBDD的一些检测问题，并能给出检测的反例［7－9］。

本文主要讨论在软件系统中进行模型检测，软件程序被表示为嵌套树和嵌套状态机2种形式。嵌套树表现了程序的所有执行路线，嵌套状态机则表现了程序语句之间的执行关系［10－12］。在嵌套树中定义μ演算（NT－μ），其基本语法单位为概要。嵌套树中多个结点可以对应于嵌套机中1个结点，概要之间存在等价关系而可以转化成一个概要类，从而在嵌套状态机上提出以概要类为基本单位的模型检测。该方法能节省检测时间，提高检测效率。

1 基本概念

1.1 嵌套树、嵌套状态机的定义

定义1（嵌套树） T＝（S，r，→，｜→）。其中，S为结点集合；r为根节点；→⊆S×S为边的变迁关系集合；｜→⊆S× （S ∪｛∞｝）为跳跃边的集合［13－14］。对于结点s，s→t表示s和t之间存在直接变迁关系，s为源结点，t为目标结点；s｜→t表示s为调用结点，t为返回结点；s｜→∞表示s为调用结点且调用没有返回。T中有限或无限道路表示为π＝s1s2…sn…，对所有i≥1，si→si＋1。

定义2（嵌套标记树） T＝（S，r，→，｜→，λ）。其中，λ：S→Σ；S为结点集合；Σ为嵌套树标记集合；λ为两者之间的一个映射，其他符号同定义1。

为了方便理解，可以用η表示边与结点之间的映射关系，η：E→｛call，return，local｝，E 为边的集合，E 被分为调用边（call）、返回边（return）和局部边（local），s→αt则η（s，t）＝α。调用边表示边的源结点为调用结点，返回边表示边的目标结点是返回结点，其余的边则为局部边。

定义3（嵌套状态机） M＝〈Vloc，Vcall，Vret，vin，κ，Δloc，Δcall，Δret〉。其中，Vloc为局部状态有限集合；Vcall为调用状态的有限集合；Vret为返回状态的有限集合；vin为起始状态。总状态集合V＝Vloc∪Vcall∪Vret∪vin。κ：V→Σ表示状态结点的标记关系。局部变迁关系 Δloc⊆ （Vloc∪Vret）×（Vloc∪Vcall）；调 用 变 迁 关 系 Δcall⊆Vcall×（Vloc∪Vcall）；返回变迁关系Δret⊆ （Vloc∪Vret）×Vcall×Vret。

嵌套状态机以嵌套树为语法基础，变迁关系被分为3类。对于状态结点s、v、t，如果（s，t）∈Δloc，则sl→oct；如果（s，t）∈Δcall，则sc→allt；如 果（s，t，v）∈Δret，则（s，t）→retv，t为最后一个未匹配的调用状态结点，返回变迁关系表现了程序的控制权由源状态结点交到返回状态结点的过程。

嵌套状态机的展开可以表示为一个非顺序的标签树TV（M），该树被看作执行树，为一个嵌套树，即嵌套状态机的展开可以表示成唯一的嵌套树。它的构成形式如下：

（1）对于树的根节点r，在M 中λ（r）＝vin。（2）如果s→αt，α∈｛call，loc｝，那么在 M 中λ（s）→αλ（t）。

（3）如果s→rett，并且存在状态结点t′使t′｜→t，那么在 M 中（λ（s），λ（t′））→retλ（t）。

1.2 概要的定义

定义4（概要） 对于一个非负整数k，k种颜色的概要是一个数组〈s，U1，U2，…，Uk〉。其中，s为根结点；U1，U2，…，Uk为 ME（s）的子集，集合中颜色标签与集合中含有的结点数量相同。

一般固定点的计算是基于状态本身的计算，而对于软件来说更注重功能的执行。在本文中定义了一个新的语法结构——概要，是针对过程内容的计算。首先定义ME（s），即结点s的匹配出口结点集合。如果t为s的匹配出口结点必须满足以下2个条件：

（1）如果s→＋t，且存在结点s′→＋s和s′｜→t。该条件表示s′为s 前驱结点，s′、s、t间有道路相连。

（2）不存在 结 点v、w，使s′→＋v→＋s→＋w 和v｜→w。该条件表示s′、s之间不存在结点v，该节点是调用结点，且相应的返回结点、其他结点均可到达。

从定义来看，从结点s出发往树的道路反方向“遇到”的第1个调用结点相对应的返回结点集合，并从该集合中剔出与结点s无道路相连的结点，可得s的匹配出口结点集合。

1.3 嵌套树的举例

一段实例程序如下：

该段程序对应的部分嵌套树如图1所示，因为该程序中采用了递归调用以及循环，所以不可能把完整的嵌套树画出来。图1中，结点｛wr｝表示write语句；结点｛en｝表示调用1段新的内容；结点｛ex｝表示从现有内容返回到原来的内容；结点｛clr｝表示clear语句；结点｛prt｝表示print语句；结点｛end｝表示return语句；而结点｛ass｝表示变量被重新赋值。

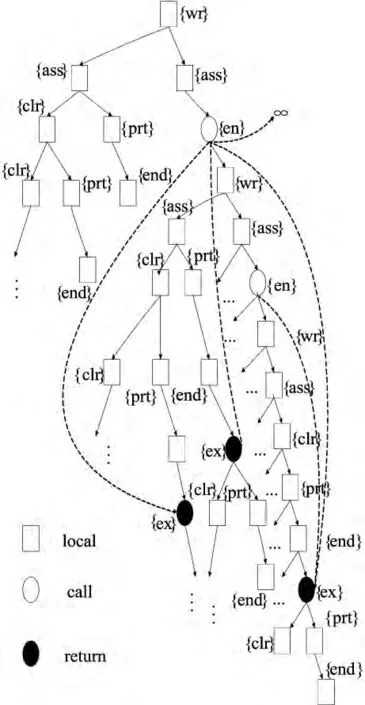
图1 实例程序的部分嵌套树

L2、L3都是变量a被重新赋值，将其归为一类。该结点｛end｝仅仅是执行return语句本身，并可以作为当前内容的结束，而结点｛ex｝则是返回原有的调用点后继续执行后面的内容，因此在图1中结点｛en｝与结点｛ex｝之间存在调用与返回的关系，两者用跳跃边（虚线箭头）相连。对于该程序每条语句执行了一个功能，如果一句语句执行了多个功能，必须把语句断开进行分解处理。对于调用语句来说，有可能能返回，有可能无返回，即此程序有可能陷于被调用的无限循环中，用∞来表示。从树的根结点到树的叶子结点为程序的一条可执行路线。

2 嵌套树的μ－演算（NT－μ）

2.1 NT－μ的语法规则

根据树结构的逻辑公式［15］，构建基于嵌套树的μ演算公式。AP为原子命题的集合，var为变量的有限集合，｛M1，M2，…｝为可数有序的标记集合。对于p∈AP，x，X∈var，k≥0，NT－μ的公式有多种基本形式，用“｜”符号隔开，定义如下：

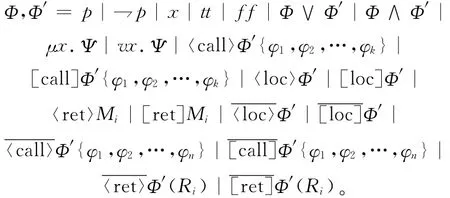
tt为所有结点都满足的公式，即所有原子公式的全集，ff为tt的补集，即空公式集。设α为call、loc、ret则为当前结点向前推α变迁关系。标记被〈call〉和［call］形式的公式所限定，标记记录当前内容调用的点，当新的被调用内容执行完毕返回时，返回标记的点继续执行。

公式Φ最大标记用mk（Φ）来表示，对于不同形式的公式有以下关系：

变量x被不动点符号限定为μx.和νx.的形式，该变量称为非自由变量。公式的自由变量集合free（Φ）有以下关系：

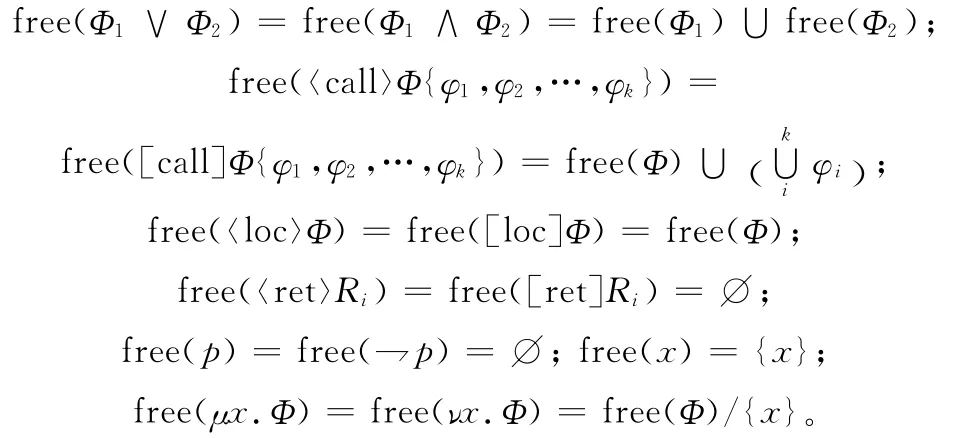
公式满足 mk（Φ）＝0、free（Φ）＝0分别为标记封闭和自由变量封闭。如果两者都成立，Φ整体被称为封闭的。

2.2 环境下NT－μ公式的语法意义

定义5（环境变量） 环境变量ε：free（Φ）→2S，Φ在环境中表示把Φ中的自由变量集合映射到嵌套树中的概要集合。［［Φ］］εT表示在环境ε满足Φ的T中的概要集合。一般T从当前内容能得到，所以可简写成［［Φ］］ε。

定义6（在环境下NT－μ公式的语法意义）对于一个概要s＝〈s，U1，U2，…，Uk〉，s∈［［Φ］］ε，当且仅当不同形式的公式满足以下条件：

（1）Φ＝p∈AP，则p∈λ（s）。

（2）Φ＝⇁p，p∈AP，则p∉λ（s）。

（3）Φ＝Φ1∨Φ2，则s∈ ［［Φ1］］ε或s∈［［Φ2］］ε。

（4）Φ＝Φ1∧Φ2，则s∈ ［［Φ1］］ε和s∈［［Φ2］］ε。

（5）Φ＝〈call〉Φ′｛φ1，φ2，…，φk｝或Φ＝［call］Φ′｛φ1，φ2，…，φk｝则分别表示s的一个调用后续结点t（sc→allt）、s的所有调用后续结点集合中的结点t满足对于以t为根结点的概要t〈t，V1，V2，…，Vn〉所有1≤i≤n，Vi＝ME（t）∩｛s′：〈s′，U1∩ME（s′），…，Uk∩ME（s′）〉∈［［φi］］ε｝。

（6）Φ＝〈loc〉Φ′或Φ＝［loc］Φ′则分别表示s的一个局部后续结点t（sl→oct）、s的所有局部后续结点集合中的结点t满足对于以t为根结点的概要t〈t，V1，V2，…，Vn〉，Vi＝ME（t）∩Ui且t∈［［Φ′］］ε。

（7）Φ＝〈ret〉Mi或Φ＝［ret］Mi则分别表示s的一个返回后续结点t（s→rett）、s的所有返回后续结点集合中的结点t满足t∈Ui。

（8）Φ＝〈loc〉Φ′或Φ＝［loc］Φ′则分别表示s的一个局部前续结点t（tl→ocs）、s的所有局部前续结点集合中的结点t满足以t为根结点的概要t〈t，V1，V2，…，Vk〉，对所有1≤i≤k，满足Vi⊇Ui。

（9）Φ＝〈call〉Φ′｛φ1，φ2，…，φk｝或Φ＝［call］Φ′｛φ1，φ2，…，φk｝则分别表示s的一个调用前续结点t（tc→alls）、s的所有调用前续结点集合中的结点t满足对于以t为根结点的概要t〈t，V1，V2，…，Vn〉∈［［Φ′］］ε所有1≤i≤n，｛s′：〈s′，V1∩ME（s′），…，Vn∩ME（s′）〉∈［［φi］］ε｝⊇Ui。

（10）Φ＝〈ret〉Φ（Mi）或Φ＝［ret］Φ（Mi）则分别表示s的一个返回前续结点t（t→rets）、s的所有返回前续结点集合中的结点，其中概要s＝〈s，U1，U2，…，Uk〉＝〈s〉且s∈Ui，概要t〈t，V1，V2，…，Vk〉满足［［Φ′］］ε。

（11）Φ＝μx.Φ′则对一个满足最小不动点的概要，且包含该概要的集合S 满足［［Φ′］］ε［x：＝S］⊆S。

（12）Φ＝νx.Φ′则对于一些 概要集合S 满足S⊆［［Φ′］］ε［x：＝S］，且最大不动点在集合S 中。

3 基于嵌套树的模型检测方法

3.1 模型检测方法的定义

嵌套树和嵌套状态机的区别在于：嵌套树的结点集合有可能是无限的，是程序的所有可能执行路线；而嵌套状态机是语句执行之间的关系，它的状态结点集合是有限的。嵌套树TV（M）（简写为T（M））是嵌套状态机M的展开形式。在嵌套状态机的基础上进行模型检测比在嵌套树上进行优势明显。嵌套树的基本单位是概要〈s，U1，U2，…，Uk〉，U1，U2，…，Uk为 ME（S）的子集。FC（s）表示离结点s最近的前驱调用结点（如果不存在FC（s）＝⊥），它的返回结点集合即为 ME（s）。嵌套树结点的不同标签对应于嵌套状态机的不同状态结点，因此可以基于嵌套状态机来判断概要的等价性，定义如下：

概要S＝〈s，U1，U2，…，Uk〉和概要S′＝〈s′，U′1，U2′，…，Uk′〉等 价，可 写 作 S≡MS′，简写为S≡S′，满足以下条件：

（1）λ（s）＝λ（s′）。

（2）λ（FC（s））＝λ（FC（s′））。

（3）对于1≤i≤k，存在一个Ωi：Ui→U′i，任意结点u∈Ui都有λ（u）＝λ（Ωi（u）），且Ui中结点个数与Ui′中结点个数相等。

由此可以看出，2个概要等价除了要有相同的“规模”，“三要素结点”（根节点、最近前驱调用结点、匹配出口结点子集）的标签也要相等。标签相等即概要中结点对应于嵌套状态机中同一个结点。判断概要结点s对应为将嵌套树中结点v为λ（s）＝κ（v）。概要全集S分为一个个概要集合，每个概要集合中的概要均等价，即将概要全集划分为互不相交的等价类。如果概要集合是等价类，那么记作该概要是等价封闭的。环境变量ε：free（Φ）→2S，如果自由变量集合free（Φ）中每个自由变量映射的概要集合都是等价封闭的，则该环境变量也是等价封闭的。

定理1 在等价封闭的环境ε中，对于NT－μ公式Φ，2个等价的概要S、S′中有一个属于，则另一个也属于（一般简写为［［Φ］］ε，嵌套树T（M）默认为当前嵌套树）。

定义7（概要类的模型检测） 设NT－μ公式Φ，一个 概 要 类 为 U ＝ 〈v，v′，V1，V2，…，Vk〉，FCM（s，s′）＝true。对1≤i≤k，Vi⊆MEM（v，v′）。概要类标注为SC。嵌套状态机中环境变量εSC为：free（Φ）→2SC，将公式中自由变量映射成概要类集合，表示在环境εSC下嵌套状态机M中满足Φ 的概要类集合（一般简写为［［Φ］］εSC，默认为当前状态机）。

（3）Φ＝Φ1∨Φ2则∪。

（4）Φ＝Φ1∧Φ2则∩。

（5）Φ＝〈call〉Φ′｛φ1，φ2，…，φk｝或Φ＝［call］Φ′｛φ1，φ2，…，φk｝则分别表示v的一个调用后续结点、s的所有调用后续结点集合中的结点t满足对于以t为根结点的概要类t＝〈t，v，V1′，V2′，…，Vn′〉∈ ［［Φ′］］εSC，对 所 有 1≤i≤n、u∈Vi′有〈u，v′，U1，U2，…，Uk〉∈［［φi］］εSC，且对于1≤j≤k，Uj＝Vj∩ME（u，v′）。

（6）Φ＝〈loc〉Φ′或Φ＝［loc］Φ′则分别表示s的一个局部后续结点t（vl→oct）、s的所有局部后续结点集合中的结点t满足对于以t为根结点的概要类t＝〈t，v′，U1，U2，…，Uk〉，Ui＝ME（t，v′）∩Vi且t ∈［［Φ′］］εSC。

（7）Φ＝〈ret〉Mi或Φ＝［ret］Mi则分别表示v 的一个返回后续结点t（（v，v′）r→ett）、s的所有返回后续结点集合中的结点t满足t∈Vi。

（8）Φ＝μx.Φ′，则对最小不动点的计算为对于［［Φ］］ε［X：＝x］，首先将∅带入x，直到该式的值SC不再改变得到最小不动点的概要类集合。

（9）Φ＝νx.Φ′，则对最大不动点的计算为对于［［Φ］］ε［X：＝x］，首先将概要类全集 SC带入x，SC直到该式的值不再改变得到最大不动点的概要类集合。

分析前驱关系NT－μ前驱公式，向前变迁产生的概要类中U1，U2，…，Un的范围会扩大。因此，无法具体限制概要类的范围，只能在已知概要类的情况下判断是否符合公式，具体判断如下：

情形1 Φ＝〈loc〉Φ′或Φ＝［loc］Φ′则分别表示v的一个局部前续结点t（tl→ocv）、v的所有局部前续结点集合中的结点t满足以t为根结点的概要类t＝〈t，v′，U1，U2，…，Uk〉，对所有1≤i≤k满足Ui⊇Vi。

情形2 Φ＝〈call〉Φ′｛φ1，φ2，…，φk｝或Φ＝［call］Φ′｛φ1，φ2，…，φk｝则分别表示v的一个调用前续结点v′（v′c→allv）、v的所有调用前续结点集合中的结点v′满足对于以v′为根结点概要类〈v′，s，U1，U2，…，Un〉∈［［Φ′］］εSC（FCM（v，s）＝true）所有1≤i≤n，｛s′：〈s′，v′，U1∩ME（s′，v′），…，Un∩ME（s′，v′）〉∈［［φi］］εSC｝⊇Vi。

情形3 Φ＝〈ret〉Φ′（Mi）或Φ＝［ret］Φ′（Mi）则分别表示v 的一个返回前续结点t（（t，v′）→retv）、v的所有返回前续结点集合中的结点t，概要类〈t，v′，V1，V2，…，Vk〉满足［［Φ′］］εSC且v∈Vi。

分析概要类的环境变量εSC为：free（Φ）→2SC，映射到概要类子集。而如果ε（X）是等价封闭的，表示每个自由变量映射的概要子集都是等价封闭的，那么映射到环境变量εSC中为等价类。

3.2 应用实例

在嵌套状态机中，用状态s1、s2、s3、s4、s5、s6、s7分别表示行L1、L2、L3、L4、L5、L6、L7。用s4′表示程序返回到原来调用执行点。局部状态集合为s1、s2、s3、s5、s6、s7，调用状态为s4，返回状态为s4′，起始状态为s1。这些状态以行为单位，对于循环、条件语句只作为控制语句来执行，作为判断语句执行的条件，而语句不执行任何具体的动作，因此不作为状态。状态与嵌套树的标签有以下对应关系：κ（s1）＝wr，κ（s2）＝κ（s3）＝mod，κ（s4）＝en，κ（s5）＝clr，κ（s6）＝prt，κ（s7）＝end，κ（s4′）＝ex。嵌套状态机Mp的变迁如下：

嵌套状态机Mp如图2所示，返回关系用虚线表示。

图2 实例程序的嵌套状态机

若要检测需求 AFcprt＝μx.（prt∨（［loc］x∧［call］δ｛x｝）），其中δ＝μy.（prt∨ （［ret］R1∧［loc］y∧［call］y｛y｝））。先找寻满足δ的概要类，最小不动点y的值带入∅。第1步得到T1＝｛〈s6，s4，｛s4′｝〉，〈s7，s4，｛s4′｝〉｝，第2步将T1带入y不再变化。计算 AFcprt＝μx.（prt∨（［loc］x∧［call］δ｛x｝）），T1′＝｛〈s6，s4，｛s4′｝〉｝即为所求。

4 结束语

本文介绍了嵌套树表示程序的方法，并给出了嵌套状态机的定义。引出了嵌套树的μ－演算（NT－μ）完整的语法结构，该语法结构有个基本单位——概要，概要是以调用返回关系为基础来表示程序的执行过程，并考虑了可能同时执行的其他过程。并在此基础上讨论了嵌套状态机上概要类的模型检测。嵌套状态机的结点和概要类都是有限的，因此该方法比基于嵌套树的模型检测的效率有所提高。

［1］ Clarke E，Grumberg O，Peled D.Model checking［M］.MIT Press，1999：1－20.

［2］ Biere A，Cimatti A，Clarke E，et al.Symbolic model checking without BDDs［C］／／Proc of TACAS’99，Netherlands.Springer－Verlag，1999：193－207.

［3］ Brayant R E.Graph－based algorithms for Boolean function manipulation［J］.IEEE Transaction on Computers，1986，35（8）：677－691.

［4］ Boiling B，Wegener I.Improving the variable ordering of OBDD is NP－complete［J］.IEEE Transaction Computers，1996，45（9）：993－1001.

［5］ Biere A，Cimatti A，Clarke E，et al.Advances in computers［M］.Academic Press，2003：42－60.

［6］ Alessandro A，Luca C.SAT－based model－checking for security protocols analysis［J］.International Journal of Information Security，2008，7（1）：3－32.

［7］ Latvala T，Biere A，Heljanko K，et al.Simple is better：Efficient bounded model checking for past LTL［C］／／International Conference on Verification，Model checking，and Abstract Interpretation，France.Springer－Verlag，2005：380－395.

［8］ Penczek W，Wozna B，Zbrzezny A.Bounded model checking for the universal fragment of CTL［J］.Fundamental Informaticae，2002，51（1）：135－156.

［9］ Wozna B.ACTL＊ properties and bounded model checking［J］.Fundamental Informaticae，2004，62（2）：1－23.

［10］ Reps T，Horaitz S，Sagiv S.Precise interprocedural dataflow analysis via graph reachabiliy［C］／／Proceedings of the ACM Symposium on Principles of Programming Languages.San Francisco：ACM，1995：49－61.

［11］ 韩江洪，刘征宇，刘晓平，等.工业控制安全研究综述［J］.合肥工业大学学报：自然科学版，2010，33（2）：161－168，173.

［12］ Alur R，Chaudhuri S，Madhusudan P.Languages of nested trees［C］／／Proceedings of the Symposium on Computer－Aided erification.IEEE，2006：329－342.

［13］ Alur R，Chaudhuri S，Madhusudan P.Software model checking using languages of nested trees［J］.ACM Transactions on Programming Languages and Systems，2011，33（5）：1501－1545.

［14］ Walukiewicz I.Monadic second－order logic on tree－like structures［J］.Theor Comput Sci，2002，275（1／2）：311－346.

［15］ Jensen T，Metayer D L，Thorn T.Verification of control flow based security properties［C］／／Proceedings of the IEEE Symposium on Security and Privacy.IEEE，1999：89－103.