医院内抗生素耐药性传染的稳定性与Hopf分支
2015-03-11马佳辉薛亚奎
马佳辉,薛亚奎
(中北大学 理学院,山西 太原030051)
0 引 言
随着在医院和社区越来越常见的细菌病原体产生的抗生素耐药性的增加,给全球人类健康带来了日益增长的威胁.抗生素耐药性细菌会引起如败血症,脓肿,伤口感染,皮肤和软组织感染和血液感染等后遗症.然而,健康人也可能携带抗生素耐药性细菌而不造成感染.人类身体的许多部位可以成为抗生素耐药性细菌的大量繁殖的地方如叶腋,会阴,腹股沟,直肠,皮肤,前鼻孔.事实上,三分之一的人类是无症状的鼻腔携带金黄色葡萄球菌[1-2].因此有限的治疗选择使预防变得越来越重要,必须在最前沿实现有效的感染控制策略.
数学模型帮助我们理解观测到的流行病学模式,疾病控制,影响疾病传播的潜在机制,还可能给我们提供疾病的控制策略.Lipsitch 和Levin[3]提出了一个简单的药物动力学和细菌种群动态的数学模型,旨在抑制治疗期间耐药性的突然出现.除了由常微分方程描述的流行病模型成为了重要的分析控制传染病传播的工具,各种各样的非线性发生率和时滞模型也被用于生物数学的模型研究中[4-8].许多专家学者也都在讨论时滞是如何影响传染病的传播的[9].本文分析了医院内传染的抗生素耐药菌的时滞模型,引入时滞代表未携带耐药菌的医护工作者成为携带耐药菌的医护工作者的潜伏时间,根据文献[10-11]本文采用来表示医院内工作人员的行为对疾病传染的抑制作用,旨在研究和讨论模型中平衡点的稳定性,分析医护工作者的行为对疾病传播的影响.
1 时滞模型
本节考虑了具有非线性发生率的院内感染的抗生素耐药性的时滞传染病模型.假设U 为未感染者,I 为耐药菌感染者,R 为康复者,A 表示每天医院新增的病人数.HU是未携带耐药菌的医护工作者,HR是携带耐药菌的医护工作者,Np为病人总数,Nh为医护工作者总数.γ1是未感染者与携带耐药菌的医护工作者接触后被感染的概率,γ2是医护工作者与耐药菌感染者接触后携带耐药菌的概率,μ 为出院率,δ 为因病死亡率,p 是治愈率,表示耐药菌感染者在医院的平均治疗时间,B 为每天进入医院的医护工作者总数,d 是医护工作者脱离携带的概率,C 为正常数.引入时滞代表未携带耐药菌的医护工作者成为携带耐药菌的医护工作者的潜伏时间.在t 时刻只有在τ 个时间单位前也就是t-τ 时刻接触感染者的未携带耐药菌的医护工作者成为了携带者,即他们在tτ时刻接触感染者时未携带耐药菌.因此携带耐药菌的医护工作者的感染项为γ2I(t-τ)HU(t-τ),正参数τ 代表潜伏时间.对于病人来说,未被感染的病人是通过接触携带耐药菌的医护工作者而被感染的.而医护工作者又是通过接触感染者才携带耐药菌的.因此,医护工作者的一些行为可能对疾病的传播有很大的影响,如消毒和洗手.所以用来表示医院内工作人员的行为对疾病传染的抑制作用.建立时滞模型如下:
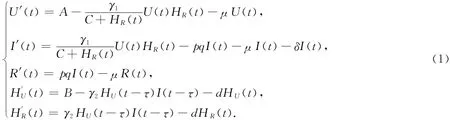
考虑到实际情况,模型中所有的参数都应为正数,所以设初始条件为U(ε)=U0,I(ε)=I0,
R(ε)=R0,HU(ε)=H0U,HR(ε)=H0R,ε∈[-τ,0].
其中,U0≥0,I0≥0,R0≥0,HU0≥0,HR0≥0.因为Np是病人总数,Nh为医院工作人员总数,且
Np(t)=U(t)+I(t)+R(t),Nh(t)=HU(t)+HR(t),因而可得

又B=dNh,易知系统(1)同样可以化为

式中:Q=pq+μ+δ.R 和HU的值可以由R =得到.考虑到实际情况,模型的解均应是正数,因此系统(2)的可行域为 和
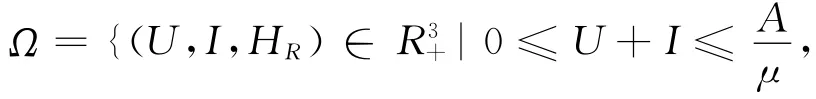
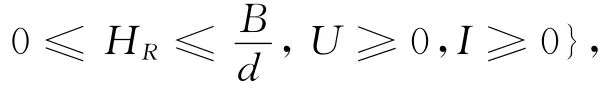
这里,R3+代表R3的非负区域.可以验证Ω 是系统(2)的非负可行域[12].是系统(2)的无病平衡点.了解疾病何时爆发是非常重要的,因此用文献[13]中的方法来计算基本再生数R0,得出

当R0≤1 时,在可行域Ω 中只存在无病平衡点;如果R0>1,无病平衡点也存在.
假设R0>1,首先考虑地方病平衡点的存在性,设地方病平衡点为E*=(U*,I*,HR*),因此有I*≠0,HR*≠0,且是系统(2)与时间无关的一个解.因为与时间无关的解在t 时刻与t-τ时刻的值相同,所以在稳定状态下求解系统(2)得:
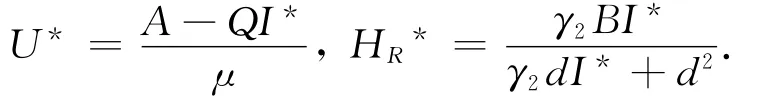
如果I*≠0,在系统(1)的稳定状态下替换U*,HR*,通过计算可得:

解方程得
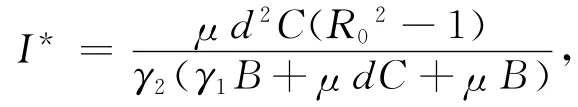
显然,当R0>1 时,I*存在且唯一.所以系统(2)地方病平衡点I*存在且唯一.
1.1 无病平衡点的稳定性
定理1 当R0<1 时,系统(2)的无病平衡点在可行域Ω 中是局部渐近稳定的,当R0>1时,不稳定.
证明 在无病平衡点处线性化系统(2)得到Jacobian矩阵:

显然,λ=-μ 是一个负实根,所有其他的根由方程(3)决定.

当τ=0时,所有的特征根均为负数.由Hurwitz判定可知,若R0<1 时,系统(2)的无病平衡点在可行域Ω 中是局部渐近稳定的,若R0>1时,不稳定.
当τ≠0时,如果R0>1,要使系统(2)在无病平衡点处不稳定只需方程(3)有一正根.首先,将方程(3)整理为如下形式:

另外,当R0<1 时,对于任意的λ≥0,F(λ)是递增的且F(λ)≥0.而G(λ)关于λ 是递减的且G(0)=Qd(R02-1)<0.因此方程(4)没有非负实根,对某一τ>0 一定有一对纯虚根.设λ=iω,不失一般性ω>0 是方程(4)的一个根.从而,有
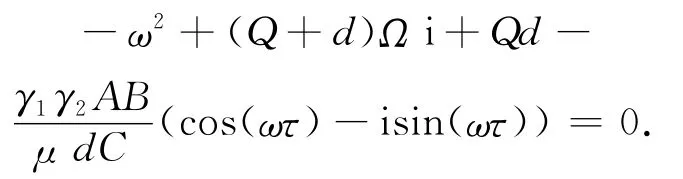
分离实虚部得:
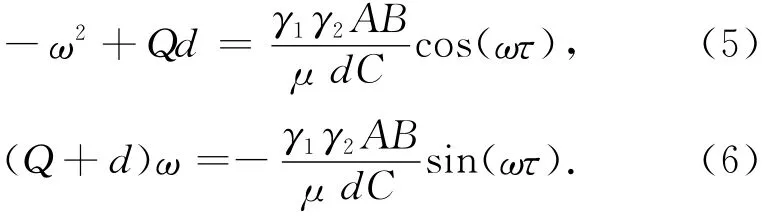
对方程(5)和(6)两边平方消去三角函数,得到一个关于ω 的四次方程:

令z=ω2,则可得
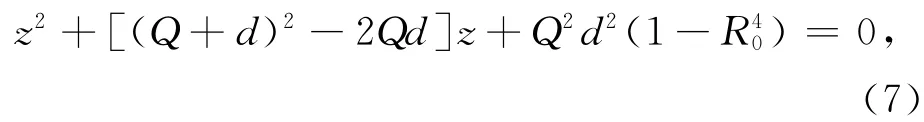
定理2 当R0≤1 时,对任意的τ,系统(2)的无病平衡点在可行域内是全局渐近稳定的.
证明 首先,把系统(2)的解转化为xt,xt=(U(t+ε),I(t+ε),HR(t+ε)),其中ε∈[-τ,0].定义Liapunov函数:

1.2 Hopf分支
首先以τ为参数分析Hopf分支发生的条件,假设R0>1,则系统(2)的地方病平衡点是存在的.
定理3 若R0>1,当τ∈[0,τ0)时系统(2)的地方病平衡点E*在Ω 中是局部渐近稳定的.若R0>R0*>1 且γ2A>dQ,当τ >τk时系统(2)的地方病平衡点处出现Hopf分支.
证明 在系统(2)中,地方病平衡点E*处的特征方程:
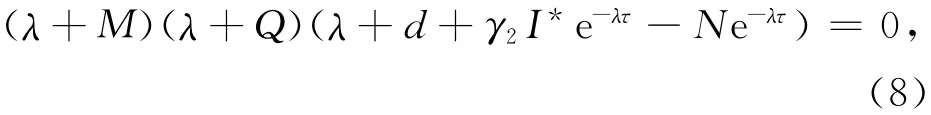

整理得
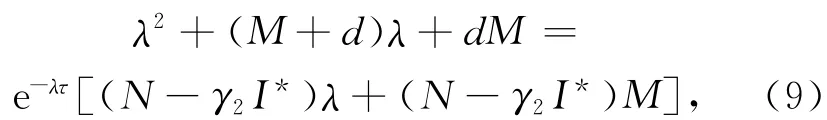
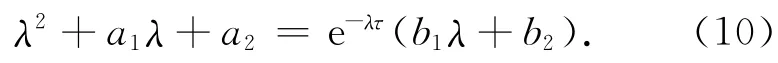
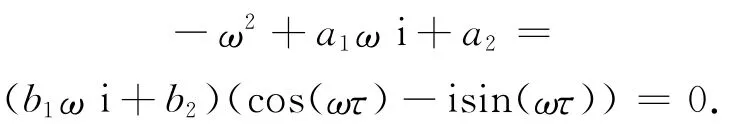
实虚部分离可得
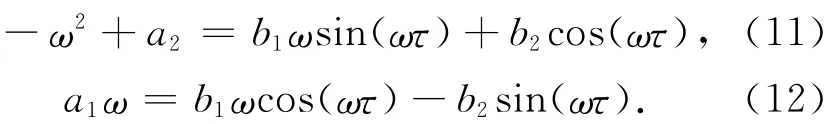
将方程(11)和(12)平方再相加得

令z=ω2,有


由于

又因为R0>1,所以,dμCR02+μB +γ1B<

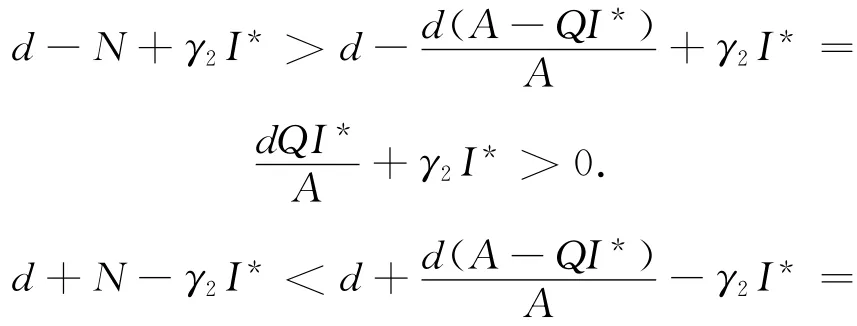


由上可得这里只需证2Ad-(dQ+Aγ2)I*<0.
接下来证明
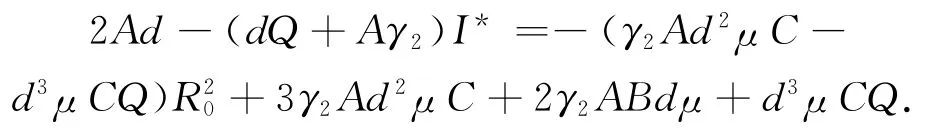
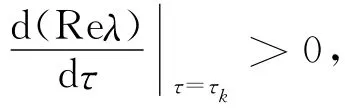
这意味着对于任意的τ>τk至少存在一个特征值有正实部,方程(10)对τ 求导,得
因此,当f(R20)=0 时,

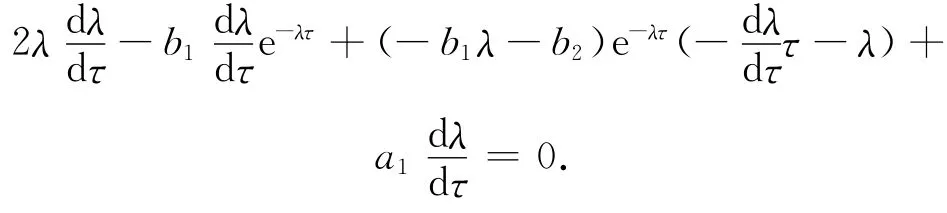
所以,dQ 且R20>R201,有

因此,方程(13)至少有一正解,即方程(10)有一对纯虚根±iω0.同时,根据方程(11)和(12)得到相应的τk>0,进而得出方程(10)有一对纯虚根

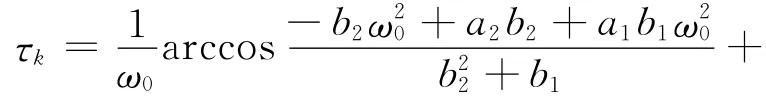
这样,
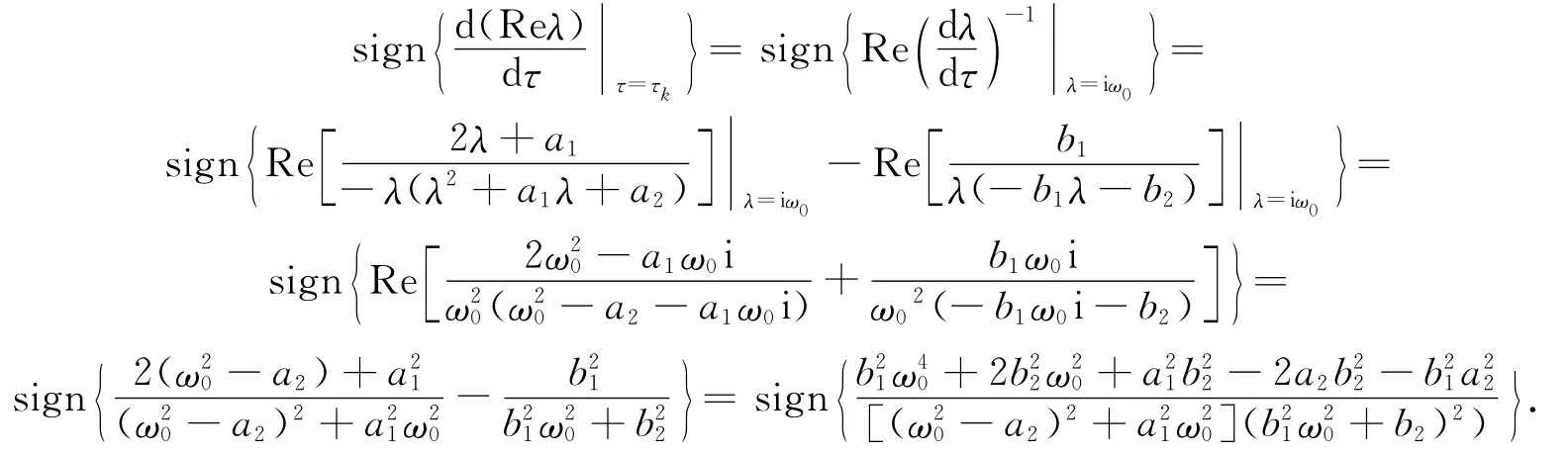

由上式得,如果M-1>0,H>0,则

因此,M-1>μR20-1,解得定义于 是,当R0>R*0且γ2A>dQ 时,推出因此,在系统(2)中,当τ=τk时,满足横截性条件和Hopf分支的发生条件.
2 数值模拟及分析
本节数值模拟研究了系统(2).根据不同数据反映出的实际情况,得出了不同的仿真结果来验证以上结论.
当R0<1 时,系统(2)的无病平衡点E0是全局渐近稳定的.令见图1.当R0>1 时,令A=35;当τ=0时,系统(2)的地方病平衡点E*是局部渐近稳定的.见图2.当τ<τ0时,系统(2)的地方病平衡点E*是局部渐近稳定的.见图3.当τ>τ0时,得出R0=5.150 3,R0*=4.941 1,显然R0>R*0,γ2A>dQ,地方病平衡点E*不稳定,在E*处发生Hopf分支.见图4.

图1 系统(2)在无病平衡点处的全局稳定性Fig.1 Global stability at the disease-free equilibrium of system(2)
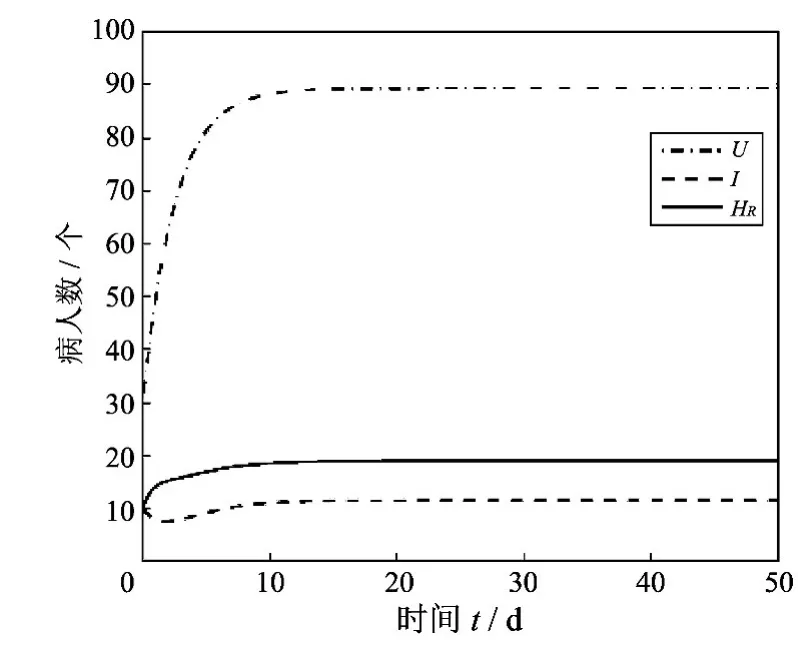
图2 τ=0 时,系统(2)在地方病平衡点处的局部稳定性Fig.2 Local stability at the endemic equilibrium of system(2)whenτ=0
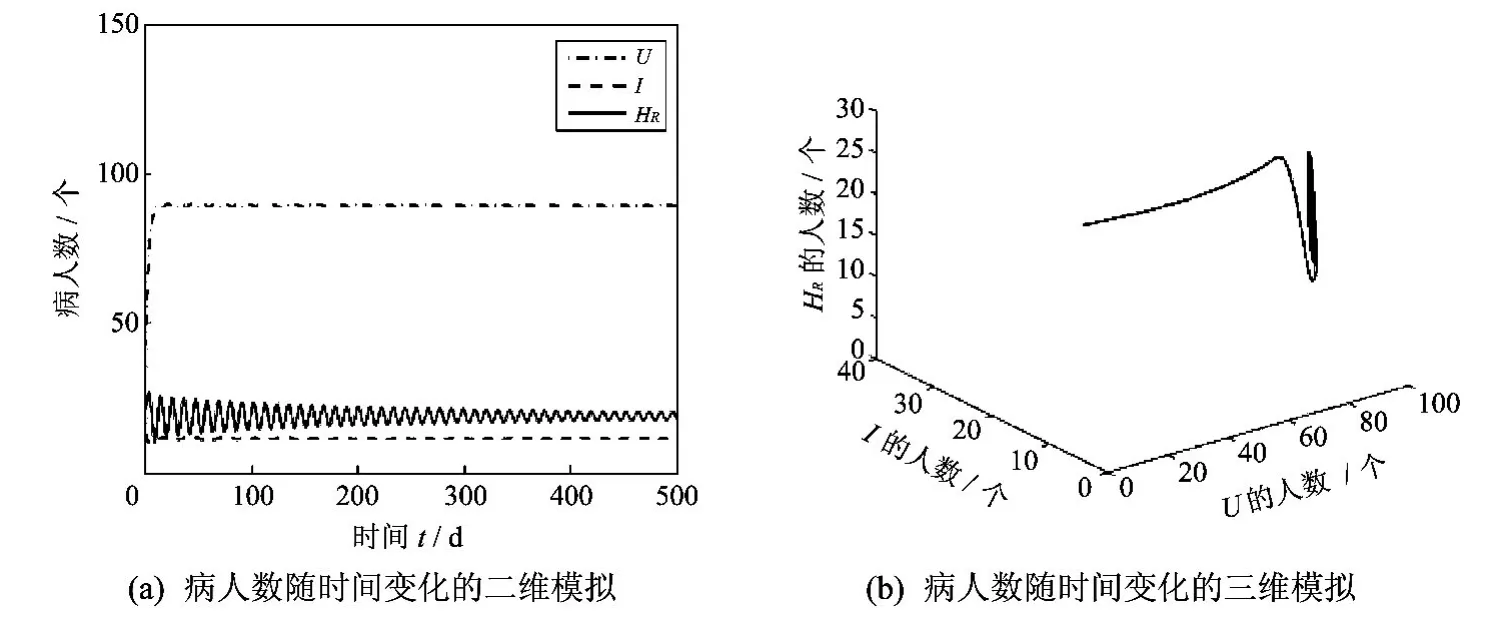
图3 τ<τ0时,系统(2)在地方病平衡点处的局部稳定性Fig.3 Local stability at the endemic equilibrium of system(2)whenτ<τ0

图4 τ>τ0时,系统(2)在地方病平衡点处的Hopf分支Fig.4 Hopf bifurcation at the endemic equilibrium of system(2)whenτ>τ0
由图1 和图2 可以看出,随着时间的增加病人人数逐步达到一个稳定的数值不再出现波动,说明系统达到了一个稳定的状态.根据所取得参数值可知,在图1 中系统的基本再生数是小于0的,可以表明系统(2)在无病平衡点处是全局渐近稳定的,而图2中根据所取参数值系统的基本再生数是大于0的且τ=0,所以系统(2)在地方病平衡点处是局部渐近稳定的.
在τ<τ0时,根据参数值可知,系统的基本再生数大于零.从图3(a)和图3(b)可以看出,随着时间的增加病人人数也在逐步趋向于一个稳定的数值,说明了系统(2)在地方病平衡点处是局部渐近稳定的.
由图4 可知,随着时间的变化,病人人数是在一个范围内不断地振荡的,并未趋于一个稳定的数值,由上面所给的参数值可得τ>τ0,R0=5.150 3,R*0=4.941 1,显然R0>R*0,γ2A>dQ,因此系统(2)在地方病平衡点处发生了Hopf分支形成了周期振荡的情况.
3 结 论
本文研究了医院内具有非线性发生率与时滞的抗生素耐药性传染病的动力学模型.用来表示医院内工作人员的行为对疾病传染的抑制作用,模型体现了医院内抗生素耐药性的传播过程.证明了模型中无病平衡点的稳定性,当τ≠0时,得到了时滞模型中Hopf分支发生的条件,系统将出现周期解.从生物学的角度来看,时滞影响了疾病的传播.因此根据不同的情况,应采取不同的方法来控制传染病的传播.
[1]Kluytmans J,van Belkum A,Verbrugh H.Nasal carriage of Staphylococcus aureus:epidemiology,underlying mechanisms,and associated risk[J].Clin Microbiol Rev,1997(10):505-520.
[2]Kuehnert M J,Kruszon-Moran D,Hill H A,et al.Prevalence of Staphylococcus aureus nasal colonization in the United States,2001-2002[J].J Infect Dis,2006(193):172-179.
[3]Lipsitch M,Levin B R.The population dynamics of antimicrobial chemotherapy[J].Antimicrob Agent Chemother,1997(41):363-373.
[4]王涛,靳祯,孙桂全.具有非线性发生率的传染病模型图灵斑图研究[J].中北大学学报(自然科学版),2011(1):1673-3193.Wang Tao,Jin Zhen,Sun Guiquan.Analysis of turing pattern in an epidemic model with nonlinear incidence rate[J].Journal of North University of China(Natural Science Edition),2011(1):1673-3193.(in Chinese)
[5]李桂花.一类具有非线性传染率的传染病模型性态分析[J].中北大学学报(自然科学版),2009(2):95-99.Li Guihua.Behavior of an epidemic model with nonlinear incidence[J].Journal of North University of China(Natural Science Edition),2009(2):95-99.(in Chinese)
[6]王建军,张晋珠,靳祯.具有饱和发生率的SIR 模型的持久性和稳定性[J].中北大学学报(自然科学版),2008(6):479-485.Wang Jianjun,Zhang Jinzhu,Jin Zhen.Analysis of permanence and stability for SIR model with saturation incidence[J].Journal of North University of China(Natural Science Edition),2008(6):479-485.(in Chinese)
[7]Xue Yakui,Li Tiantian.Stability and Hopf bifurcation for a delayed SIR epidemic model with logistic growth[J].Abstract and Applied Analysis,2013:916130.
[8]Xue Yakui,Wang Xiaoqing.Stability and local Hopf bifurcation for a predator-prey model with delay[J].Discrete Dynamics in Nature and Society,2012:252437.
[9]Wei H M,Li X Z,Martcheva M.An epidemic model of a vector-borne disease with direct transmission and time delay[J].J.Math.Anal.Appl,2008(342):895-908.
[10]Meng X Z,Chen L S,Cheng H D.Two profitless delays for the SEIRS epidemic disease model with nonlinear incidence and pulse vaccination[J].Appl.Math.Comput,2007(186):516-529.
[11]Xu R.Global dynamics of an SEIS epidemiological model with time delay describing a latent period[J].Math.Comput.Simulat,2012(85):90-102.
[12]Harrus S,Baneth G.Drivers for the emergence and re-emergence of vector-borne protozoal and bacterial diseases[J].Int.J.Parasitol,2005(35):1309-1318.
[13]P van den Driessche,James Watmough.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Math.Biosci,2002(180):29-48.
[14]LaSalle J P.The Stability of dynamical systems[M].Philadelphia:SIAM,1976.
[15]DiendonnéJ.Foundations of modern analysis[M].New York:Academic Press,1960.
