一类具有时滞的食饵-捕食者模型的时空斑图
2015-03-11解博丽王志军
解博丽,王志军
(1.中北大学 机电工程学院,山西 太原030051;2.中北大学 理学院,山西 太原030051)
0 引 言
近年来,比例依赖的食饵-捕食者模型一直是重要的模型之一.为了很好地描述食饵-捕食者模型的物种之间的真正的生态相互作用,文献[1]提出了下面的捕食模型并做了一定的研究.
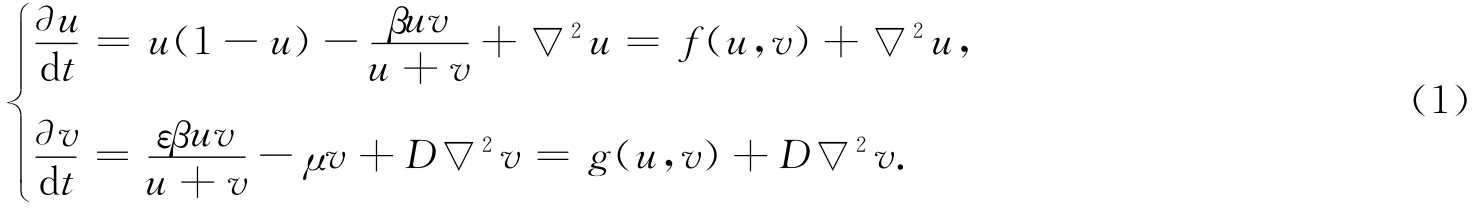
时滞在许多生物动力系统中起重要作用,尤其是在生态系统中,时间延误因怀孕被包含在一些食饵-捕食者模型中.针对这种拖延对捕食系统的动态行为的影响,很多论文对此进行了研究[2-13].
然而,针对具有时滞的比例依赖捕食模型的动力学行为,尤其是针对该模型的空间斑图研究得比较少.因此,本文目标是研究具有时滞的比率依赖捕食模型,更具体地,本论文主要研究该模型的空间斑图.该模型由式(2)给出

式中:τ 是一个大于零的常数.
扩散方程模型(1)降为常微分方程模型为

首先需给出系统(2)的初始条件为
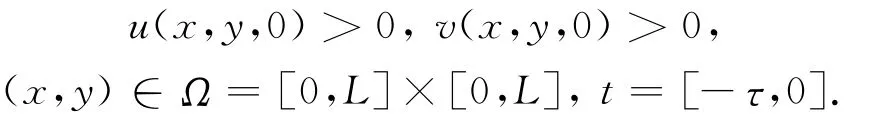
同时假设没有外界输入,即Zero-flux Neumann边界条件(零流边界条件),那么边界条件为
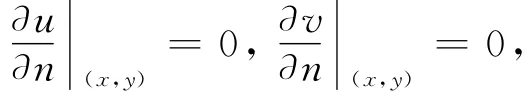
式中:Ω 是空间区域;L 表示系统(3)的大小为正方形域;n是边界∂Ω 的外侧单位矢量.
1 模型分析
本节将讨论模型(2)的稳定性.很容易看出,模型(2)和模型(3)具有相同的平衡点.从生物学角度出发,关心的是正平衡点的性态.模型(3)的正平衡点为E*=(u*,v*),其中

很容易看出来,要保证u*和v*是正的条件为
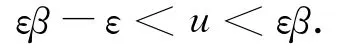
下面主要讨论正平衡点E*=(u*,v*)处的动力学性态.图灵不稳定性指的是非空间模型(3)在正平衡点是稳定的,空间模型(2)在正平衡点处是不稳定的.
非空间模型(3)在正平衡点处的稳定性,由下面的数学表达式来保证

这里

这里主要研究带有时滞和扩散的食饵-捕食者模型的空间斑图结构.根据文献[14-15],假设τ足够小,作如式(6)变换来替换v(x,y,t-τ).


把模型(6)代入模型(2)中,得到对系统(7)进行泰勒级数的展开,并忽略高阶非线性项,系统(7)变为

既然在E*=(u*,v*)处满足f(u*,v*)=0和g(u*,v*)=0,那么在E*=(u*,v*)处,得到
系统(9)为

为了考察当稳定的平衡点E*=(u*,v*)受到小扰动δu和δv 时系统的变化,令u=u*+δu 和v=v*+δv,得到
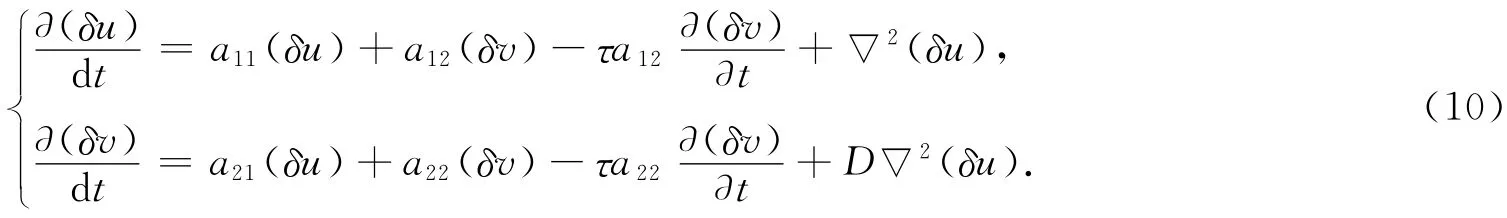
从(10)中,得到

当τ很小时,系统(8)可以用来分析系统(2)的动力学性态.

假设系统(10)的解有如下的形式式中:λ是扰动的增长率;δu*和δv*表示振幅;kx和ky是波数.把方程(12)代入系统(11),可以得到系统(11)在平衡点E*处的特征方程

这里

且

方程(13)的解为

空间模型(2)在正平衡点的不稳定性,指的是tr(Jk)<0 和det(Jk)>0 至少有一个不满足.因此,考虑以下两种情况下的不稳定性:
1)det(Jk)>0是不满足的;
2)tr(Jk)<0是不满足的.
1.1 由反应扩散引起的不稳定性
首先考虑det(Jk)>0是不满足的.
因为τ 是一个很小的数,并且a22=-
如果det(Jk)>0是不满足的,即det(Jk)<0是满足的,那么需要满足条件Da11+a22>0.
通 过 得 到 det (Jk) =
从这个方程可以看出,det(Jk)是不依赖于τ 的,det(Jk)只和扩散有关系.
既然对于某些k,tr(Jk)<0是满足的,从式(14)中,注意到下面的条件是必须满足的:(a11+
因此有下面的结论:对于系统(2),图灵不稳定的条件由式(17)给出

为了更好地观察交叉扩散的作用,画出了色散关系图如图1 所示.固定参数值ε=0.8,μ=7.35,β=10,τ=0.2.从图1 可以看出,随着参数D 值的增加,得到了图灵模式,即Re(λ)>0.

图1 方程(13)的色散关系图Fig.1 An illustration of the dispersion relation from the equation(13)
1.2 由时滞引起的不稳定性
考虑第二种情况,tr(Jk)<0是不满足的.
由上 述 讨 论 可 以 得 到,当(a11+a22)+τ(a11a12-a12a21)>0 不等式成立时,tr(Jk)<0是不满足的.也就是说在这种情况下,τ >因此在接下来的讨论中,τ必须满足:
如果det(Jk)>0 是满足的,那么需要条件Da11+a22>0 是成立的.通过得到det(Jk)=的最小值,相应地能得到k2的值,即.把k2c代入det(Jk)>0,得到(Da11+a22)2<4D(a11a22-a12a21).
因此有下面的结论:对于系统(3),不稳定的条件由式(18)给出

2 空间斑图
在实践中,可以将连续形式的无限维问题转化为离散形式的有限维问题.实际上,由二维反应扩散系统所定义的连续问题可以由M×N 格子组成的离散区域解决.每两个格子间的空间距离定义为步长Vh.在离散系统中,描述扩散的拉普拉斯算子用有限差分计算,即导数是Vh 上的差分逼近.当Vh→0 时,差分就可以近似代替导数.时间演化也离散化,即时间步长为Vt.时间演化可以用欧拉法解决,也就是说下一个时间步长的状态依赖前一个时间步长.固定参数值Vh=1,Vt=0.01和M=N=200.注意到,当Vh,Vt 减小时,模型(2)的动力学行为不再发生任何改变.
2.1 由反应扩散引起的不稳定性的斑图
选择满足条件(17)的合适参数,并将这种情况下的斑图称为图灵斑图.固定参数值为:ε=0.8,μ=7.35,β=10,τ=0.2,得到临界值τc=0.341 182 867,取τ=0.2<τc.这里,(u*,v*)=(0.187 5,0.016 581 632 65).
从图2 中可以看到,初始不规则的斑图最终演化产生了规则的点状斑图、条状和点状共存的斑图、以及条状斑图,他们布满了整个区域,且系统的动力学性态不再发生改变.
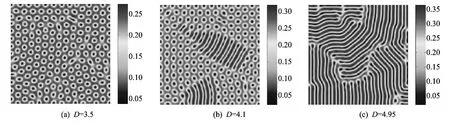
图2 食饵在空间分布的演化图Fig.2 Evolution in the spatial distribution of the prey
2.2 由时滞引起的不稳定性的斑图
选择满足条件(18)的合适的参数.选择参数为ε=0.8,μ=7.4,β=10,D=11.5,τ=0.9,得到临界值τc=0.801 8,取τ=0.9>τc.这里,(u*,v*)=(0.25,0.020 270 270 27).

图3 食饵u的演化图Fig.3 Evolution diagram of the prey u
由图3 可以看出,在一段时间之后,有相同半径的斑点慢慢地占据整个域.斑图的内部是黑色的,因此也形象地称之为“黑眼斑图”.
3 结 论
本文主要讨论了具有交叉扩散和时滞的食饵-捕食者模型的动力学性态.通过图灵不稳定性的条件,得到了两种不同类型的斑图.具体地,在由反应扩散引起的不稳定的条件下,即det(Jk)<0,通过一系列的数值模拟,得到了参数空间中丰富的图灵结构,分别有点状斑图、条状斑图以及点状和条状共存的斑图结构.在由时滞引起的不稳定性的条件下,即tr(Jk)<0,通过数值模拟,得到了“黑眼斑图”.
尽管需要更多的工作,原则上,似乎延迟和扩散能够产生多种不同的时空格局.由于这些原因,可以预测,延迟和扩散可被视为复杂时空外观的重要机制动态的生态模式.
[1]Liu Panping.Pattern formation of a predator-prey model[J].Nonlinear Analysis:Hybrid Systems,2009(3):177-183.
[2]Nindijin A F,Aziz-Alaoui M A,Cadivel M.Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay[J].Nonlinera Anal.Real World Appl.,2006(7):1104-1118.
[3]Xu Rui,Chen Lansun.Persistence and stability for a two-species ratio-dependent predator-prey system with time delay in a two-patch environment[J].Comput.Math.Appl.,2000,40:577-588.
[4]Yafia R,Adnani F,Alaoui H.Limit cycle and numerical simulations for small and large delays in a predatorprey model with modified Leslie-Gower and Hollingtype II schemes[J].Nonlinear Anal.Real World Appl.,2008(9):2055-2067.
[5]Ruan S.On nonlinear dynamics of predator-prey models with discrete delay[J].Math.Modelling Nature Phenom,2009(4):140-188.
[6]Sun Guiquan,Chakraborty A,Liu Q X,et.al.Influence of time delay and nonlinear diffusion on herbivore outbreak[J].Communications in Nonlinear Science and Numerical Simulation.2014,19(5):1507-1518.
[7]Xu Rui,Ma Zhien.An HBV model with diffusion and time delay[J].J.Theoret.Biol.2009,257:499-509.
[8]Su Ying,Wei Junjie,Shi Junping.Hopf bifurcations in a reaction-diffusion population model with delay effect[J].J.Differential Equations.2009,247:1156-1184.
[9]Yang Y R,Li W T,Wu S L.Stability of traveling waves in a monostable delayed system without quasimonotonicity[J].Nonlinear Anal.R.W.A.2013,14:1511-1526.
[10]Yang Yunrui,Li Wantong,Wu Shiliang.Exponential stability of traveling fronts in a diffusion epidemic system with delay[J].Nonlinear Anal.R.W.A.2011,12:1223-1234.
[11]Breda D,Visetti D.Existence,multiplicity and stability of endemic states for an age-structured S-I epidemic model[J].Math.Biosci.2012,235:19-31.
[12]Tian Canrong.Delay-driven spatial patterns in a plankton allelopathic system[J].National Institutes of Health.2012,22(1):013129.
[13]Wang Yi,Cao Jinde,Sun Guiquan,et al.Effect of time delay on pattern dynamics in a spatial epidemic model[J].Physica A,2014,412:137-148.
[14]Sen S,Ghosh P,Riaz S,et.al.Time-delay-induced instabilities in reaction-diffusion systems[J].Phys.Rev.,2009,E80,046212.
[15]Ghosh P.Control of the Hopf-Turing transition by time-delayed global feedback in a reaction-diffusion system[J].Phys.Rev.,2011(E84):016222.
