基于涡流检测的曲面涂层厚度影响因素分析
2015-03-11杨晓辉
杨晓辉,金 永,杨 凌
(中北大学 电子测试技术国家重点实验室,山西 太原030051)
0 引 言
在现代工业中,为使材料表面具有一定的强化、绝缘、隔热等功能,可在材料表面形成一层或多层不同厚度的涂层.如果涂层厚度未达到规定要求,会对其物理性能产生不良影响.因此,材料表面涂层的厚度是重要的产品质量指标,必须要对材料表面涂层厚度进行检测[1-2].常用的涂层测厚方法有射线法、超声法、激光法、红外法、涡流法等,而对于较薄涂层厚度的测量,涡流法因具有快速、准确和无接触等特点,成为最佳检测方法之一[3].涡流检测基于电磁感应原理,当检测线圈靠近导体试件时,会在试件内部感应出涡流,任何使涡流信号发生改变的因素都会引起线圈阻抗的变化[4].
目前涡流测厚的研究大多针对平板检测对象,文献[5-6]中以平板为检测对象,将模型简化为二维或轴对称来进行分析,得到线圈阻抗变化和涂层厚度的对应关系.文献[7]中由于曲面曲率半径较大,可对曲面问题采用近似方法化为平板进行求解,但当曲面曲率半径相对线圈半径不够大时,这种简化会引起很大误差.在实际工程检测中,经常会遇到对曲率半径各不相同的复杂曲面进行涂层测厚,对于曲面导体,无法将其简化为二维轴对称模型,且各介质内部具有复杂的边界条件.针对以上实际问题,本文在平板涂层测厚的基础上,建立了曲面三维涡流场有限元模型,分析了影响曲面涂层测厚的因素,为曲面涂层测厚提供了参考依据.
1 电磁场有限元基本理论
在电磁场数值计算中,麦克斯韦方程组是有限元仿真的基础[8-9].在工程实践中,根据具体情况给定的初始条件和边界条件,引入矢量磁势A和标量电势φ 进行数值求解,将其代入麦克斯韦的偏微分方程中,经过推导得到磁场偏微分方程式和电场偏微分方程式.
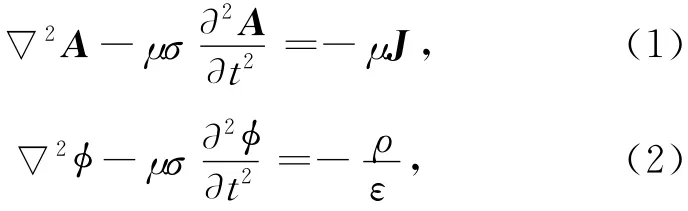
式中:μ和ε分别为介质的磁导率和介电常数;▽2为拉普拉斯算子.
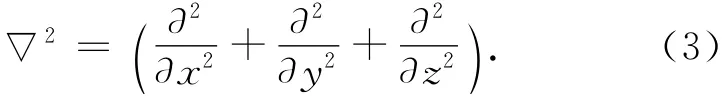
ANSYS正是采用有限元的数值计算方法对式(1)和(2)进行了求解,得到磁势和电势的场分布值,并通过后处理得到电磁场的电感、电容等.
2 曲面涂层测厚建模与求解
利用ANSYS软件进行三维涡流场的仿真分析,选取单元类型和实常数定义,建立了三维涡流场的有限元模型.进行网格划分,然后加载激励和边界条件,最后求解并查看仿真结果[10-12].
2.1 有限元模型的建立
图1 为导体试件涡流检测的三维有限元模型,由于模型几何边界面关于场源的中心轴呈旋转对称,因此建立三维整体模型.

图1 有限元模型(隐去空气域)Fig.1 Finite element model(faded air field)
图1 中,线圈内径为1mm,外径4.77mm,厚度5.1mm,匝数400 匝.导体试件材料为奥氏体不锈钢SUS304,厚2mm.
定义材料属性:导体试件电导率σ =1.4×106s/m,相对磁导率μ =1;线圈电导率σ=5.8×107s/m,相对磁导率μr =1;空气相对磁导率μr =1.
在三维建模中,选取SOLID97 单元进行建模,其中包括线圈、试件及近场空气域,远场区空气用INFIN111单元.表1 详细列出了各实体区域的单元类型及自由度设置.

表1 单元类型及节点自由度Tab.1 Unite type and node degrees of freedom
为了提高计算精度,在网格生成上采用映射-自由混合划分方式.其中,线圈和导体试件由于形状规则,可采用映射网格划分;对于近场区空气,由于其形状不满足映射划分的要求,因此采用自由网格划分;而远场区空气可在近场区空气的单元形状的基础上,用映射方式生成网格.
2.2 边界条件
边界条件的设定是为了确保求解的唯一性.在利用有限元求解时,区域内部各介质交界面上满足磁感应强度切向分量的连续性条件,属于自然边界条件,系统自动满足,而对于最外层边界上应该设定磁场为0.此外,在模型的远场空气边界面上施加无限远场标志.
2.3 施加载荷与求解
线圈所加激励为频率5 000Hz 的正弦交流30V 电压源.在加载电压的过程中,需要耦合线圈上所有节点的CURR 自由度.施加的边界条件及载荷如图2 所示.

图2 施加边界条件后的模型Fig.2 Model of imposing boundary condition
3 仿真结果与分析
在涡流检测中,线圈与导体试件之间发生耦合作用,在导体内部感应出近似呈环状的电涡流,如图3 所示.其中最大的电涡流密度Je=1.28×107A/m2.
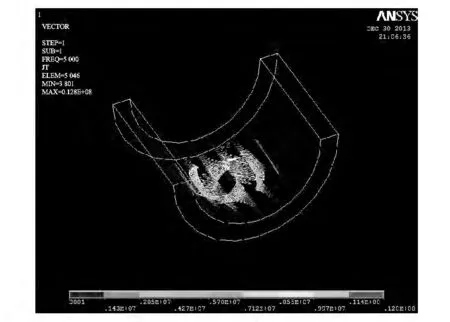
图3 涡流密度矢量分布图Fig.3 Eddy current density vector maps
3.1 曲面曲率半径对涡流信号的影响
曲面曲率半径的不同,对涡流检测信号的影响程度也不同.如图4 所示,保持提离距离不变,仅改变曲率半径的大小,观察曲率半径的变化对涡流信号的影响.
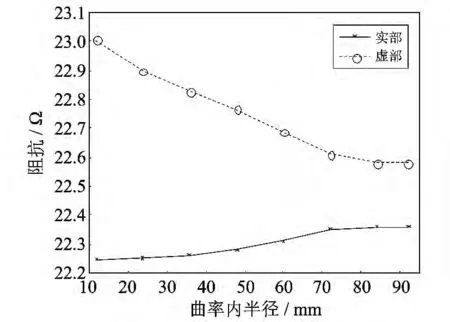
图4 曲率变化对阻抗信号的影响Fig.4 Influence of curvature on impedance signal
图4 中,当曲面曲率的内半径小于80 mm时,涡流信号的变化较大;当曲率的内半径大于80mm 时,涡流信号趋于稳定.所以,当曲面曲率的内半径大于80mm 时,曲率变化对涡流信号的影响基本可以忽略.
3.2 曲面厚度对涡流信号的影响
在涡流检测中,当探头的工作频率确定后,涡流在导体试件中的有效透入深度是确定的.当导体试件厚度小于或者大于该透入深度时,都将对涡流信号产生影响,因此需要分析其厚度对涡流信号的影响.
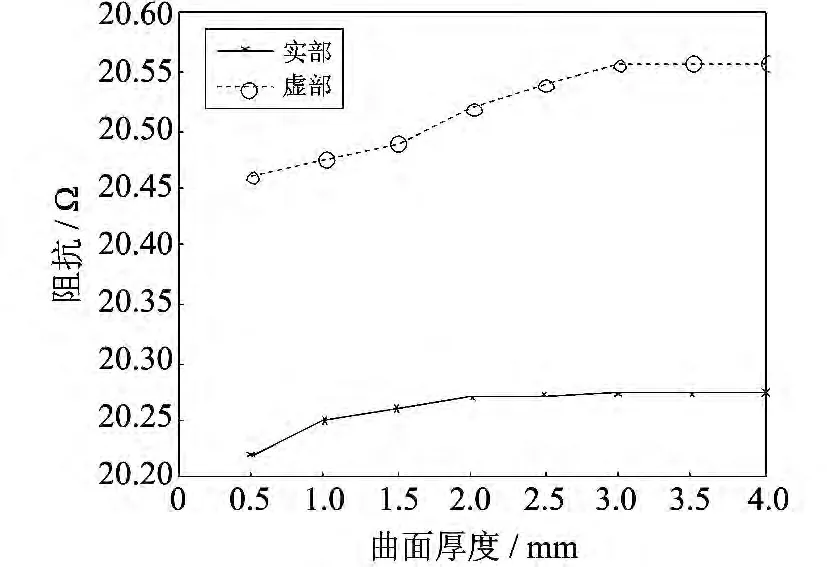
图5 曲面厚度对阻抗信号的影响Fig.5 Influence of thickness measured body on impedance signal
如图5 所示,随着曲面厚度的增加,检测线圈阻抗实部和虚部都逐渐增大,当曲面厚度在3mm 以上时,涡流信号的变化较小.可见,曲面厚度有一个临界值,大于该厚度值时,试件对涡流信号的影响较小.
在曲面涂层厚度的测量中,涂层的厚度实质上等效于检测线圈到导体试件表面的提离距离.提离距离的变化即为涂层厚度的变化,也可称之为涂层厚度的检测精度.通过上述结论可以得出:曲面的曲率半径和厚度的变化都会对检测精度产生较大的影响,因而在曲面涂层测厚时,应考虑上述两个因素对涡流信号的影响.
3.3 探头提离变化对涡流信号的影响
在保证曲面曲率半径及厚度对涡流信号没有影响的情况下,改变提离距离,得到涂层厚度(提离距离)与线圈阻抗变化的对应关系.其中提离距离从0mm 逐渐增加至4.5mm,间隔0.5mm 取一个点.图6 为检测线圈随提离距离变化的归一化阻抗图.
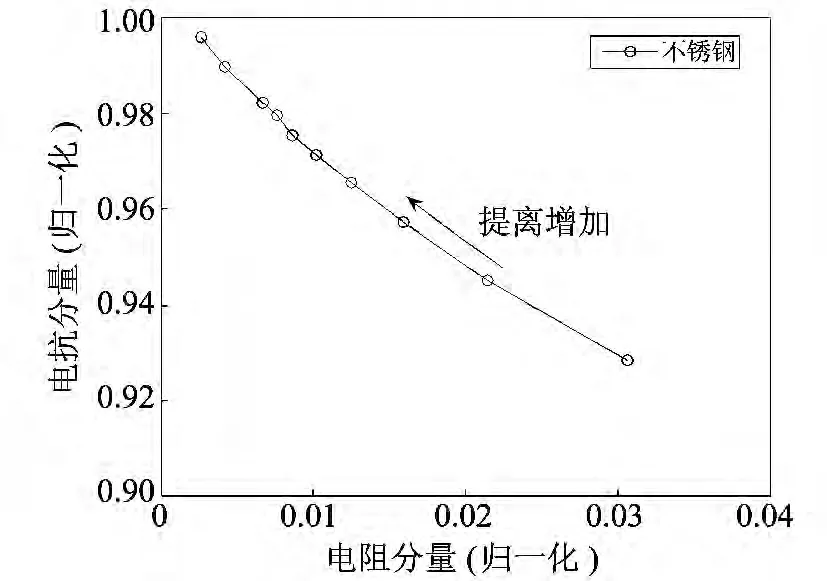
图6 不同提离距离的归一化阻抗图Fig.6 Normalized impedance diagram
从图6 中可以看出,随着提离距离的增加,检测线圈的阻抗实部在减小,虚部在增大.起点为零提离时线圈阻抗的归一化值终点逼近于线圈空载时的值,阻抗轨迹近似为一条直线,而且提离效应更多地反映在线圈的阻抗变化上.
4 结 论
本文采用有限元分析软件ANSYS建立了曲面导体涡流检测的三维有限元模型,通过仿真分析计算了曲面的曲率半径、厚度和提离距离的变化对检测线圈阻抗变化的影响,得到检测线圈的归一化阻抗图.仿真结果表明:利用ANSYS 软件分析影响曲面涂层厚度测量的因素是可行的,且曲面的曲率半径和厚度在一定范围内对涡流信号有较大的影响,在实际曲面涂层检测中应予以矫正.
[1]Yin W,Peyton A J.Thickness measurement of nonmagnetic plates using multi-frequency eddy current sensors[J].NDT & E,International,2007,40(1):43-48.
[2]胡鹏,王召巴,张东利.大量程涡流测距探头的仿真设计[J].传感器与微系统,2012,31(8):103-106.Hu Peng,Wang Zhaoba,Zhang Dongli.The simulation design for eddy current probe of wide detecting range[J].Transducer and Microsystem,2012,31(8):103-106.(in Chinese)
[3]吴鑫,谢基龙,石坤.脉冲涡流参数对金属侧厚影响的仿真分析[J].北京交通大学学报,2012,36(1):122-126.Wu Xin,Xie Jilong,Shi Kun.Simulation analysis of effects of pulsed eddy current parameters on metal thicknes measurement[J].Journal of Beijing Jiaotong University,2012,36(1):122-126.(in Chinese)
[4]刘利秋.基于电涡流传感器测厚及材质鉴别的研究[J].沈阳航空工业学院学报,2006,23(5):84-86.Liu Liqiu.The research on thickness measurement and material discrimination based on electrial eddy sensor[J].Journal of Shenyang Institute of Aeronautical Enigineering,2006,23(5):84-86.(in Chinese)
[5]任吉林,俞佳,唐继红.放置式涡流线圈测厚的数值分析[J].南昌航空大学学报(自然科学版),2008,22(3):37-40.Ren Jilin,Yujia,Tang Jihong.Numerical value analysis of thickness measurement on placement eddy current probe coil[J].Journal of Nanchang Hangkong University(Natural Science),2008,22(3):37-40.(in Chinese)
[6]Peter J S.Nondestruetive Evaluation:Theory,Techniques,and Applications[M].New York:Marcel Dekker,2002:1-2.
[7]陈德智,邵可然.管道裂纹涡流检测线圈阻抗信号的快速仿真[J].电工技术学报,2000,15(6):75-78.Chen Dezhi,Shao Keran.Rapid simulation of the coil impedance signal for eddy cueernt inspection of the tube with a crack[J].Transanctions of China Electrotechnical Society,2000,15(6):75-78.(in Chinese)
[8]王燕礼,朱有利,杨红军.管道涡流信号的有限元仿真研究[J].计算机仿真,2013,30(5):425-433.Wang Yanli,Zhu Youli,Yang Hongjun.Finite element method simulation research on eddy current signal in pipeline[J].Computer Simulation,2013,30(5):425-433.(in Chinese)
[9]任吉林,曾亮,张丽攀.碳纤维复合材料涂层厚度涡流法测量的研究[J].仪器仪表学报,2011,32(12):2262-2268.Ren Jilin,Zeng Liang,Zhang Lipan.Research on thickness measurement of carbon fiber composite’s coating with eddy current testing[J].Chinese Journal of Scientific Instrument,2011,32(12):2262-2268.(in Chinese)
[10]张玉华,孙慧贤,罗飞路.小曲率半径弧面涡流检测中探头提离干扰的抑制方法研究[J].中国电机工程学报,2009,29(27):126-132.Zhang Yuhua,Sun Huixian,Luo Feilu.Suppression method of a probe-coil’s lift-off noise for the curved specimen with small curvature radius in eddy-current testing[J].Proceedings of the CSEE,2009,29(27):126-132.(in Chinese)
[11]周杰,张德均,陈庭勋.基于电涡流的铜膜测厚研究[J].现代电子技术,2010(7):179-182.Zhou Jie,Zhang Dejun,Chen Tingxun.Research on thickness measurement of copper film based on eddy current[J].Modern Electronics Technique,2010(7):179-182.(in Chinese)
[12]张玉华,罗飞路,孙慧贤.飞机轮毅涡流检测中探头提离效应的分析与抑制[J].仪器仪表学报,2009,30(4):786-790.Zhang Yuhua,Luo Feilu,Sun Huixian.Suppressing probe-coil’s lift-off effect on inspection of aircraft wheel hubeddy current technique[J].Chinese Journal of Scientific Instrument,2009,30(4):786-790.(in Chinese)
