一种混合人工免疫算法的研究

张安玲，邓启森

（1．长治学院 数学系，山西 长治046011；2．中北大学 计算机与控制工程学院，山西 太原030051）

0 引 言

人工免疫理论是借鉴生物免疫系统的机理来建立人工免疫系统，并用于解决现实问题的理论和方法，是继神经网络、遗传算法后，从生物系统提取的又一智能化理论，是目前人工智能研究的热点之一．人工免疫系统的应用研究涉及控制、优化、机器学习、故障诊断和机器人路径规划等多个领域［1－4］．

人工免疫算法为基于种群的随机搜索算法，它具有强大的信息处理和问题求解能力等优点．但它在进化中可能会出现退化现象，从而导致收敛速度较慢，不能以较大的概率收敛到全局最优值，算法的收敛性和稳定性有待进一步分析，以及算法的执行效率还有待提高［5］．国内外学者为此展开了许多研究：Gong和Jiao等人提出了一种SRCPA 算法［6］，有效地提高了算法的运行速度．Toyoo Fukda等在文献［7］中给出了一个关于信息熵的免疫算法．韩国Jang 和Chun博士等在文献［8］中提出了利用高级免疫算法进行永磁同步电机参数优化设计．文献［9］提出了DKBAIA 算法，能改善算法的收敛性．文献［10］基于克隆选择原理和免疫网络理论，实现了一种多模态免疫优化算法．

本文欲在提高收敛速度和收敛性能两方面作些探讨，从人工免疫算法和经典算法的特点出发，设计了一种基于殴氏距离的自适应人工免疫算法和BFGS算法相联合的混合算法．此算法继承了人工免疫算法的群体搜索性，具有全局优化能力；同时在人工免疫算法中引入BFGS算法，使之能发挥传统数值优化算法在运算速度和求解精度上的优势，从而有效地提高算法的局部搜索能力和运行效率．

1 混合人工免疫算法

1．1 标准人工免疫算法

标准人工免疫算法是将生物免疫学和计算机科学相结合而形成的．该算法的具体步骤如下［11］：①抗原识别．输入目标函数．②初始化．随机产生初始群体，生成N 个抗体．③计算抗体的适应度．④记忆库更新．⑤抗体的选择（促进和抑制）．⑥交叉和变异．⑦群体更新．⑧终止．若达到终止条件则停止迭代，否则转到第③．

1．2 BFGS算法

BFGS算法是由Broyden，Fletcher，Goldfarb等于1970年提出的［12］．目前BFGS算法被公认为是最好的拟牛顿法［12］．

BFGS算法的计算步骤：

1）给出x0∈Rn，H0∈Rn×n，0≤ε＜1，k：＝0．

2）如果‖gk‖ ≤ε，则停止；否则，计算dk＝－Hkgk．

3）沿方向dk作线性搜索求αk＞0，令xk＋1＝xk＋αkdk．

4）利用

求Hk＋1，使得拟牛顿条件Hk＋1yk＝sk成立．

5）若k：＝k＋1，则转第2）．

BFGS算法不仅计算精度高，而且具有很好的数值稳定性．

1．3 混合免疫算法

1．3．1 参数设置

1）编码方式本文采用的均是二进制编码．

2）交叉率pc和变异率pm［13］

式中：0≤ki≤1，i＝1，2，3，4；f（x）表示适应度；表示平均适应度；fmax（x）表示最大适应度．

3）抗体浓度和抗体期望繁殖率

定义1 在特定的抗体群中，给定抗体v，其与抗体群中任一抗体w 的殴氏距离记为d（v，w）＝‖v－w‖［14］．

定义2 抗体v，w 的适应度记为Fv和Fw，对应所求解的问题给定适当的常数r＞0，m＞0，若有

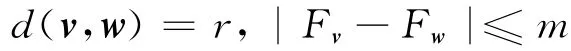
成立，则称抗体w 与抗体v相似；与抗体v相似的抗体（包括v）的个数称为抗体v 的浓度，记为Cv［14］．

定义3 对于特定的规模为N 的抗体群，抗体v的期望繁殖率可用式（3）算出

式中：Fv为抗体v 的适应度；Cv为抗体v 的浓度［14］．

1．3．2 混合人工免疫算法

标准人工免疫算法是一种全局性概率搜索算法，但它的收敛性、稳定性以及算法的执行效率还有待进一步提高．为此，对标准人工免疫算法进行了改进，以提高算法的收敛性和运行速度．

1）抗原识别．

2）初始化．随机产生初始群体，生成N 个抗体．

3）抗体适应度的计算．

4）记忆库更新．用最大适应度值对应的抗体替换记忆库中比其适应度值低的任一抗体．记n（n＜N）为记忆库中抗体的规模．

5）抗体的选择（促进和抑制）．利用式（3）所得的抗体v的期望繁殖率进行选择．

6）交叉和变异．分别采用1）和2）自适应变化的交叉率和变异率对抗体进行单点交叉和变异．

7）BFGS算法运算．对群体中每个抗体以概率ps进行一次BFGS 算法运算，将子代取代父代；对记忆库中的每个抗体进行一次BFGS算法运算，将子代取代父代．

8）计算抗体的适应度．

9）群体更新．用记忆库中的抗体代替群体中适应度值比其低的抗体．

10）终止．若达到终止条件则停止迭代，且输出记忆库中的最好抗体作为最优解；否则转到第4）．

注1 在此混合算法中，每个抗体是以概率ps进行BFGS算法运算，这样提高了算法的运算效率．

注2 用记忆库中的抗体替换群体中比其适应度值小的抗体，增强了记忆库中抗体的功能，避免了迭代过程中因随机性而使最好抗体丢失，从而提高了全局收敛性．

2 数值实验

为了验证本文算法的有效性，给出以下测试函数．

利用Matlab对以上4个函数分别运算30次，与各测试函数真实最优解的方差及平均收敛时间如表1 所示．

表1 方差与平均收敛时间Tab．1 Variance and average convergence time

从表1 可以看出，本文算法计算出的函数最优解与真实最优解的方差较小，说明本文搜索到的平均最优解与真实最优解偏离程度较小，数据波动小，求解精度高，稳定性好．从平均收敛时间可知，算法收敛速度较快．

为了体现出本文算法对函数的进化过程，对4个测试函数的函数值进化曲线分别从30次的运算中随机选取1次与文献［15］进行比较，具体的对比结果如图1～图4 所示．搜索能力和BFGS算法的局部超线性收敛性．

图1 函数f1 进化曲线Fig．1 Function f1evolution curve

图2 函数f2 进化曲线Fig．2 Function f2evolution curve

图3 函数f3 进化曲线Fig．3 Function f3evolution curve

图4 函数f4 进化曲线Fig．4 Function f4evolution curve

从以上4个函数的进化曲线可以看出，本文算法对函数f1，f2，f3能很快找到最优解，迭代次数非常少；而文献［15］分别得运行400，100，150，300次左右才能找到解．针对很难极小化的函数f4，本文算法也比文献［15］的迭代次数少．对这些多极值、难以极小化的函数该算法都能以较少的进化代数搜索到全局最优解，表明它的收敛速度快，稳定性好，从而体现出BFGS 算法嵌入到人工免疫算法中，局部收敛性得到了很大的改善．

利用本文算法和文献［15］算法分别对以上测试函数针对算法的成功率进行了比较，比较结果如表2 所示．

从表1 数据可以看出，本文算法收敛到最优解的次数明显多于文献［15］，这说明本文算法的收敛性、稳定性较好，从而表明在算法中嵌入BFGS算法提高了人工免疫算法的收敛速度和收敛性能．该算法充分发挥了人工免疫算法的全局

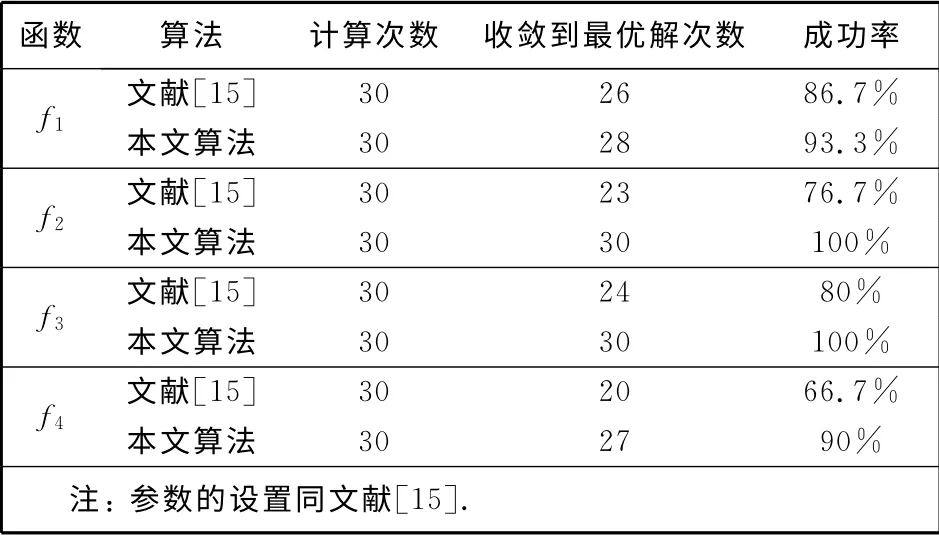
表2 本文算法与文献［15］算法的比较结果Tab．2 Comparison between algorithm of this paper and algorithm of the literature［15］

3 结 论

本文针对人工免疫算法局部收敛性较弱的缺陷，提出了一种基于经典优化算法——BFGS 算法的改进人工免疫算法．该算法在保持人工免疫算法的全局搜索能力的基础上，在局部嵌入了BFGS算法，从而加强了人工免疫算法的局部搜索能力，整体上提高了人工免疫算法的执行效率．典型函数的实验数据表明：该算法在成功率、收敛速度和求解精度上都有了提高，并且具有很强的鲁棒性，为函数优化提供了一种方法．该算法还可以应用到求解非线性方程、方程组等具体问题中．本文算法是加强了人工免疫算法的局部搜索能力，而如何进一步提高人工免疫算法的后期搜索能力，是下一步的研究工作．

［1］柴争义，王献荣，王亮．用于异常检测的实值否定选择算法［J］．吉林大学学报，2012，42（1）：176－181．Chai Zhengyi，Wang Xianrong，Wang Liang．Real－value negative selection algorithm for anomaly detection［J］．Journal of Jilin University，2012，42（1）：176－181．（in Chinese）

［2］Biswal B，Biswal M K，Dash P K，et al．Power quality event characterization using support vector machine and optimization using advanced immune algorithm［J］．Neurocomputing，2013，103：75－86．

［3］Nicholas W，Pradeep R，Greg S，et al．Artificial immune systems for the detection of credit card fraud：an architecture，prototype and preliminary results［J］．Information Systems Journal，2012，22（1）：53－76．

［4］Chen J，Lin Q，Ji Z．A hybrid immune multiobjective optimization algorithm［J］，European Journal of Operational Research，2010，204（2）：294－302．

［5］王磊，肖人彬．基于免疫记忆的人工免疫算法模型及其应用［J］．模式识别与人工智能，2002，15（4）：385－390．Wang Lei，Xiao Renbin．An algorithmic model of artificial immune system based on immunological memory［J］．Pattern Recognition and Artificial Intelligence，2002，15（4）：385－390．（in Chinese）

［6］Gong M G，Jiao L C，Zhang L N，et al．Immune secondary response and clonal selection inspired optimizers［J］．Progress in Natural Science，2009，19（2）：237－253．

［7］Dasgupta D．Artificial Immune Systems and Their Applications［M］．Bedin Heidelberg：Springer－Verlang，1999．

［8］Jang S，Chun M K K，Hyun－Kyo J．Shape optimization of electromagnetic devices using immune algorithm［J］．IEEE Transactions on Magnetics，1997，33（2）：1876－1879．

［9］郑日荣，毛宗源，罗欣贤．基于欧氏距离和精英交叉的免疫算法研究［J］．控制与决策，2005，20（2）：161－169．Zheng Rirong，Mao Zongyuan，Luo Xinxian．Research on euclidean distance and King－crossover－based immune algorithms［J］．Control and Decision，2005，20（2）：161－169．（in Chinese）

［10］何珍梅，徐雪松．一种多模态函数优化的免疫算法［J］．南昌大学学报（工科版），2008，30（1）：83－86．He Zhenmei，Xu Xuesong．A immune algorithm for multi－modal function optimization［J］．Journal of Nanchang University（Engineering ＆ Technology Edition），2008，30（1）：83－86．（in Chinese）

［11］李翠云．基于DNA 的人工免疫算法及应用研究［D］．杭州：浙江大学，2013．

［12］陈宝林．最优化理论与算法［M］．北京：清华大学出版社，2005．

［13］Srinivas M．A daptive probability of crossover and mutation in genetic algorithms［J］．IEEE Trans．Syst．Man．Cybern．，1994，24（4）：655－667．

［14］郑日荣，毛宗源，罗欣贤．改进人工免疫算法的分析研究［J］．计算机工程与应用，2003，39（34）：35－37．Zheng Rirong，Wao Zongyuan，Luo Xinxian．A study on modified artificial immune algorithms［J］．Computer Engineering and Applications，2003，39（34）：35－37．（in Chinese）

［15］赵伟，刘雪英．基于最速下降法的人工免疫算法［J］．内蒙古工业大学学报，2009，28（2）：94－97．Zhao Wei，Liu Xueying．The artificial immune algorithm based on the steepest descent method［J］．Journal of Inner Mongolia University of Technology，2009，28（2）：94－97．（in Chinese）