四点插值法在柔性织物曲面模拟中的应用
2015-03-10杨晓波
杨晓波
(浙江财经大学东方学院,浙江 杭州 310012)
四点插值法在柔性织物曲面模拟中的应用
杨晓波
(浙江财经大学东方学院,浙江 杭州 310012)
为进一步提高柔性织物的仿真度,提出一种基于四点插值法的柔性织物曲面模拟方法。具体研究过程是:首先分析了基于四点插值法的织物曲面模型,利用四点插值法细分柔性织物的曲线和曲面,最后通过四点插值法进行曲面的拼接和局部修改,并采用对比实验验证四点插值法的可行性。研究结果表明,所提出的基于四点插值法的柔性织物实体模拟方法,模拟准确度达到95%以上,从而验证了该方法的可行性。
四点插值法;柔性织物;曲面模型;实体模拟
对于变形曲面重建方法的研究是近年来计算机仿真领域的研究热点。传统的模拟仿真方法由于没有将变形物体的材料属性因素考虑在内,因而难以获得真实的变形效果。为此,相关学者已在此领域进行了深入研究。Terzopoulos[1]提出了一种较通用的曲面弹性变形模型,该模型可形象地描述各种柔性材料变形过程,但也存在着一些缺陷,如计算效率较低,计算稳定性较差,不能完全表述曲面实际变形等;Breen等[2]已成功将粒子模型运用于柔性织物仿真之中,取得了十分逼真的模拟效果,但采用粒子模型方法同样存在一定缺陷,主要表现在计算耗时较大且计算效率较低,仍不能精确地反映变形曲面的真实变形过程,无法对复杂的曲面进行处理等;1994年,Terzopoulos等又提出了基于能量模型的动态NURBS曲面[3],该方法保留了NURBS曲面模型的基本信息,具有良好的整体柔顺性,但由于该模型对物体曲面的要求较高,要求曲面形态尽可能光滑,而真实材料的曲面受表面纹理和光照条件等因素影响,较难达到模型要求,因而仿真准确度较低,另外模型本身较复杂,计算时间较长,实时性仿真效果较差;半刚性样条模型在NURBS曲面模型基础上进行了改进[4],该模型能够在保证长度不变的前提下进行弯曲变形,符合织物保持长度的物理特性,计算也较为简化,能产生悬垂织物变形时特有的褶皱等效果,但也存在一定缺陷,如交互的选择物理参数仍有待研究,如何在提高计算效率的同时保证曲面质量的平衡等。
柔性织物是一种典型的变形曲面,选用何种模型构造柔性织物曲面是织物仿真模拟的关键问题。本文拟根据织物自身和仿真要求,利用四点插值法进行织物曲面模拟研究,以期获得较为满意的效果。
1 四点插值法的织物曲面模型
织物曲面模拟研究领域一直都受到各国学者的广泛关注。Fugerson首先在飞机设计中提出,将曲线、曲面表示为参数向量的函数形式[5];Coons提出由4条边界曲线确定参数曲面,进而表示完整曲面的方法[6];Versprille[7]等研究出非均匀有理 B 样条的一整套理论和方法,并使之成为行业标准。上述方法均是定义在矩形参数域上,无法有效地表示任意拓扑形状的曲面。当表示复杂物体表面时,通常采用逐片构造的方法,必须对曲面片进行裁剪,还需考虑片间的光滑拼接,处理起来相当困难且耗时。为满足织物快速真实模拟和复杂曲面造型的需要,本文提出利用四点插值法进行三维柔性织物曲面表示的方法。
四点插值法是由四点插值曲线张量积形式生成的,是基于四边域网格的插值型细分方法,选择此方法的主要原因是:采用四边域网格特性,能够自然地反映织物经向、纬向编制结构,且可通过构造合适的边界条件,解决不同曲面间光滑拼接的问题。
在分析织物物理模型的基础上,本文构造出基于四点插值法的织物变形曲面模型。构造过程如图1所示。从图可知,织物变形曲面的构造过程包括4个步骤。首先将织物离散成四边域网格,如图1(a)所示,图中每根经纱和纬纱的交叉点被看作为质点,这些质点聚合在一起形成质点集,反映了邻近矩形区域的质量分布,当织物在外力作用下发生形变时,质点间的相互位置也在发生变化,主要表现为3种形式,分别为伸缩、弯曲和剪切,如图1(b)、(c)、(d)所示。为表示3种形变的外作用力,可利用DeRose等[8]提出的能量函数模型来表示,本文将在此基础上,利用四边域网格分析织物产生的形变情况。
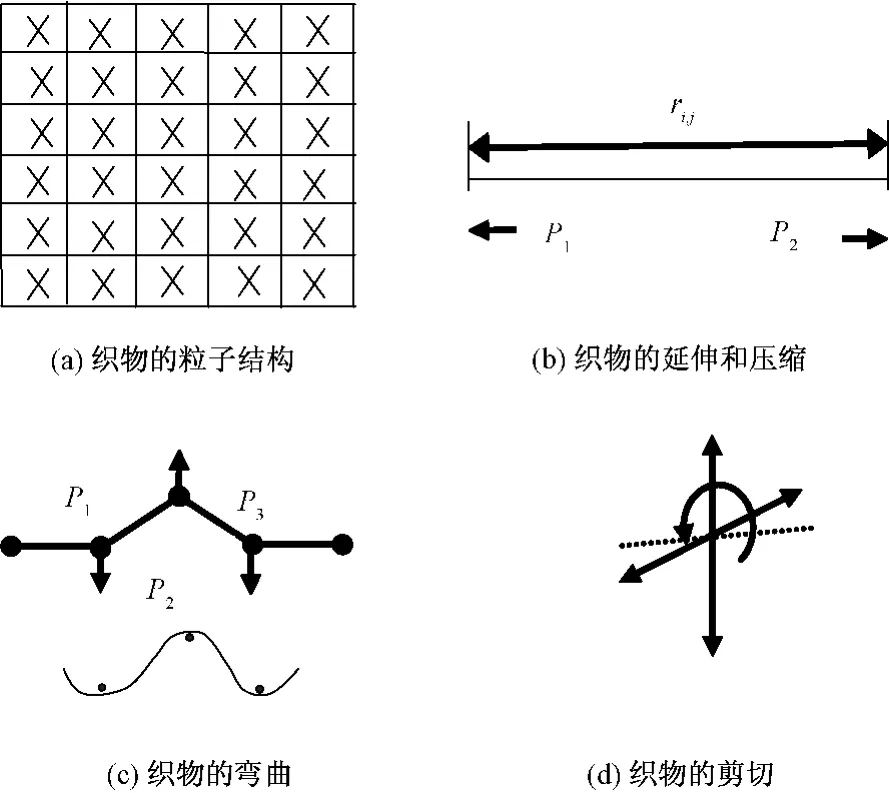
图1 基于四点插值的织物变形曲面构造过程Fig.1 Surface construction process of fabric deformation based on four point interpolation.(a)Particle structure of fabric;(b)Extension and compression of fabric;(c)Curving fabric;(d)Shearing fabric
2 四点插值法细分曲线和曲面
Dyn等[9]首先提出了四点插值细分算法,并对算法进行了验证,该算法的关键是如何求出控制顶点的值,由于控制顶点受多种因素影响,使得生成的曲线连续性和收敛性难以保证,另外,该算法要求控制点分布均匀,对非均匀分布的控制点拟合效果较差,故本文对该算法做了进一步改进。
从初始控制点列{Pi}出发,计算产生出新的插值点,如式(1)所示:

式中:Pi+1表示新插入的点,位于顶点Pi之后;s表示算法的收敛性系数。从式(1)可知,如果在Pi和Pi+1之间插入新顶点,需要由它的相邻结点,即Pi-1,Pi,Pi+1和 Pi+24 个点决定。
下面定义第v次细分后的顶点集,记为{Pvi},则第v+1步细分后所得顶点为:

当v=0时,初始值为P0i=Pi。当v趋于无穷时,将得到一个无穷点列。另外,经过计算,当,或0<s<时,所获得的极限曲线是连续的。
利用曲线张量积可以计算四点插值细分曲面,初始值可记P0i,j,其中 i= -2,…,m+2,j=-2,…,n+2,由第v步网格点集计算获得第v+1步的网格集合,具体方法是:先从i下标出发,利用式(2),在点Pvi,j与 Pvi+1,j间插入新点;再从 j下标出发,在点Pvi-1,j与 Pvi+2,j间插入新点,这样便生成k+1层的网格点集,如式(3)所示。
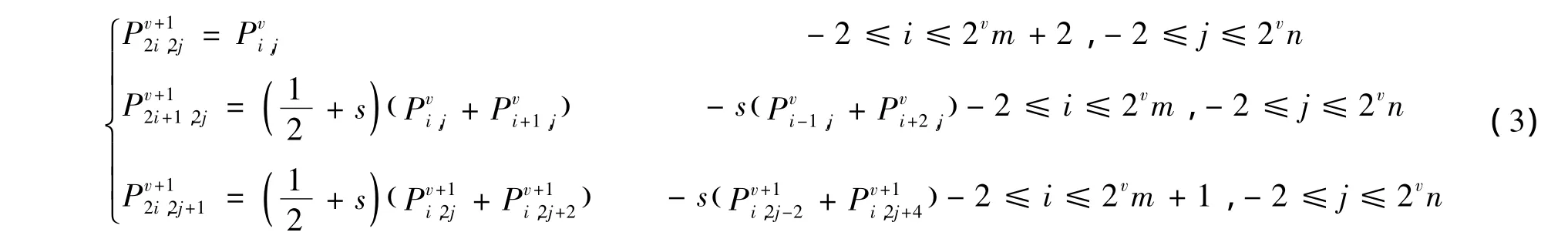

图2 四点细分曲面构造过程Fig.2 Fourpoint subdivision surface construction processes
从图可知,利用四点插值法细分曲面,一般情况下经过2步迭代后,可获得较为理想的曲面。
3 曲面拼接和局部修改
三维服装的基本单元是复杂的二维织物(衣片),因而在进行织物曲面模拟时,需要考虑衣片间的约束关系和相对位置,在此基础上形成初始控制网格,初始网格拼接时需保证衣片间的光滑拼接。本文利用四点细分造型方法,通过构造合适的边界条件,实现曲面间的光滑拼接。本文以2个曲面片S1、S2为例,讨论曲面拼接的构造方法。
3.1 四点细分曲线边界点的生成方法
采用传统方法构造边界点运算量较大[10-11]。本文在传统方法基础上进行了改进。首先利用中垂线定理求出4个插值点,再利用四点插值法对初始插值点进行均匀分布,改进方法只需简单地线性运算即可构造边界点,且系统开销较小,这样可大大减少计算耗费。采用改进后的方法可求得点列另一端的Pn+1,再利用已求出的 P-l,Pn+1,用同样方法可求出 P-2,Pn+2。
3.2 四点细分曲面边界点的构造
根据四点插值曲线边界点的构造方法,可类似进行四点细分曲面边界点的构造。首先构造初始网格控制点阵中各行、列的边界点,再由已产生的边界点和初始控制网格上的点,用同样的构造方法求出其余4个角点上的边界点。在求4个角的边界点时,对于同一位置,按照行或列方向求出的结果并不相同,一般做法是对2种构造结果值进行平均。
3.3 曲面的拼接
构造了曲面的边界点后,再分析2个曲面片间的光滑拼接条件。曲面片S1由初始插值点阵列{pi,j,i=0,…,n1,j=0,…,m1}给出,曲面片 S2由初始插值点阵列 {qi,j,i=0,…,n2,j=0,…,m2}给出,其中 pi,m1=qi,0。为使 S1、S2在 pi,m1或 qi,0所确定的四点法曲线处实现C1连接,曲面片应取如下边界条件。
曲面片S1的边界条件为:
1)由 pi,m1,i=0,…,n 构成的曲线边界一侧,取pi,m1-1=qi,1,pi,m1-2=qi,2,其中 i=-2,…,n+2;
2)再由 pi,0,i=0,…,n 构成的曲线边界一侧,取 pi,-2,pi,-1,i=-2,…,n+2 的值,并由上述提到的边界点构造方法给出。
曲面片S2的边界条件为:
1)由 qi,0,i=0,…,n 构成的曲线边界一侧,取qi,-2=pi,m1-2,qi,-1=pi,m1-1,其中 i=-2,…,n+2;
2)再由 qi,m-2,i=0,…,n 构成的曲线边界一侧,取 qi,m2-2=qi,m2-1,其中 i=-2,…,n+2 的值。
按照上述方法构造的边界条件对曲面片S1、S2进行细分,曲面片S1、S2将实现Gl连续拼接,如图3所示。

图3 曲面片间光滑拼接过程Fig.3 Smooth splicing process between patches.(a)Initial stitching patches;(b)Stitching patches after subdivision once;(c)Final stitching smooth surface
图3示出曲面片间光滑拼接的过程,结合上述方法,可实现多个曲面片间的拼接,最终形成整个三维服装初始控制网格。
3.4 曲面的局部修改
局部修改在改进三维服装曲面过程中非常重要,下面将利用本文提出的方法对服装曲面的局部特性进行修改。
服装曲面的初始控制点列为P0i,j,当点列当中的某点 Pi,j发生改变,改动后的值记为 P'i,j,则其变化量为 △P=Pi,j-P'i,j,这一局部特性的改变将影响整个细分曲面。
从前述可知,通过计算曲线张量积可得到四点细分曲面,因此,可先从曲线的局部修改做起,进而覆盖到整个细分曲面。
首先,初始网格点集被第1次细分,利用四点细分算法,可以生成4个新的点,计算过程见式(4)。
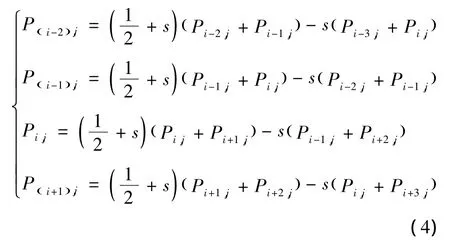
当点 Pi,j被改动为 P'i,j时,产生的变化对 Pi,j之后的影响如下:
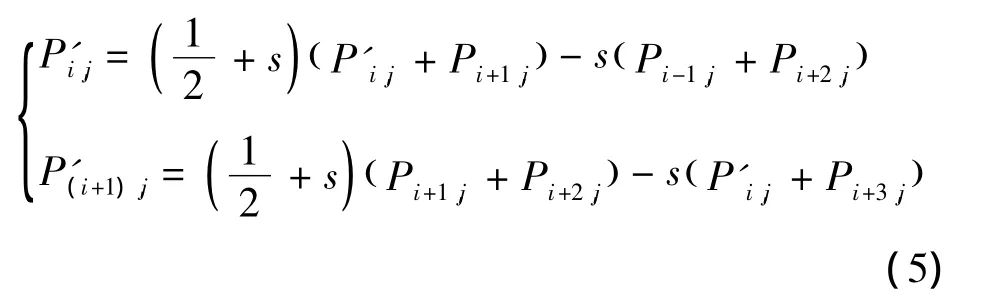
结合式(4)和式(5),可得:
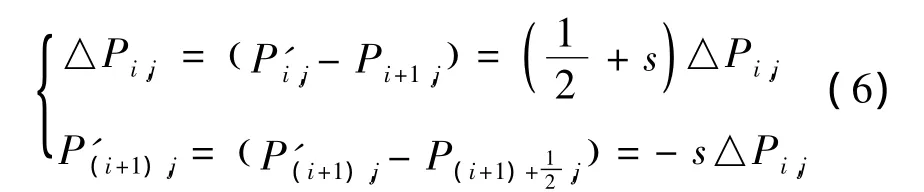
由式(6)可知,点 Pi,j的变化对 Pi,j和 P(i+1),j的影响较大,曲线在 Pi,j到 Pi+2,j之间的变化情况为:
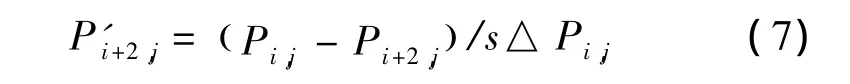
由式(7)可知,由于受到△Pi,j的影响,曲线在Pi,j到 Pi+2,j之间的部分会有较大变化。
当初始网格点集被细分2次后,Pi,j的变化将对曲线在 Pi+2,j和 Pi+3,j之间产生影响,如式(8)所示。
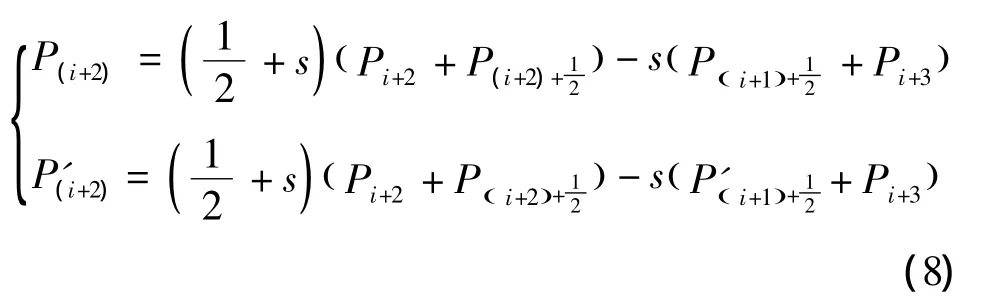
由于在实际应用过程中,s一般取值为1/12,因此点 Pi,j的改动对曲线段 [Pi+2,j,Pi+3,j]和[Pi-3,j,Pi-2,j]的影响非常小,在实际应用中常常可忽略。
上述对四点细分曲线局部性质的讨论,可很容易推广到整个四点细分曲面,即当改变控制点列中的点Pi,j时,对整个四点细分曲面有显著影响的区间为 [Pi-2,j,Pi+2,j] × [pi,j-2,Pi,j+2]。
4 对比实验
为验证四点插值法的可行性,本文以单色女裙作为样本进行实际模拟。首先确定女裙衣片与三维人体模型,通过光滑拼接条件和细分方法对衣片进行拼接,构造三维服装模拟初始网格,在此基础上通过局部修改对服装进行真实感模拟,模拟效果见图4。织物模拟准确度的评价标准是通过最终模拟效果与织物实体悬垂外观进行对比,模拟效果越接近织物实体外观,模拟准确度越高。
另外,实验过程中还采用Terzopoulos曲面弹性变形模型进行模拟,实验样本同样采用单色女裙,并将模拟结果与本文方法进行对比,模拟准确度通过模拟图像与织物实体悬垂外观图像进行对比得到,结果如表1所示。
从表1可知,在相同织物质点数的条件下,不论是模拟时间和模拟准确度,本文方法都优于Terzopoulos法。
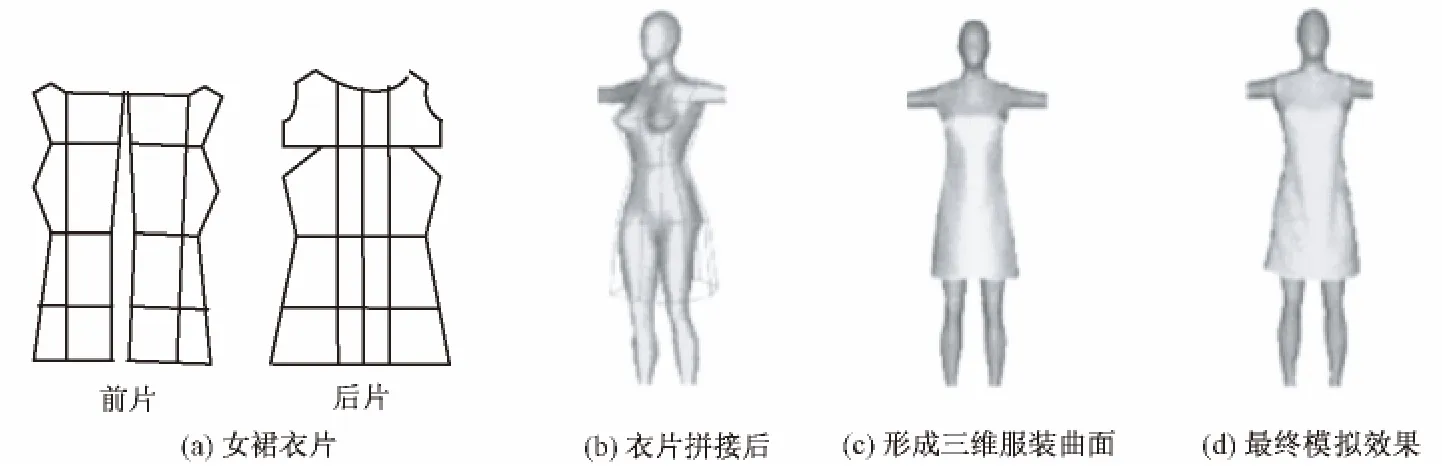
图4 三维服装模拟过程Fig.4 3-D garment simulation process.(a)Skirt front patch and rear patch;(b)Initial mesh of skirt stitching;(c)Formation of 3-D garment surface;(d)Final simulation results
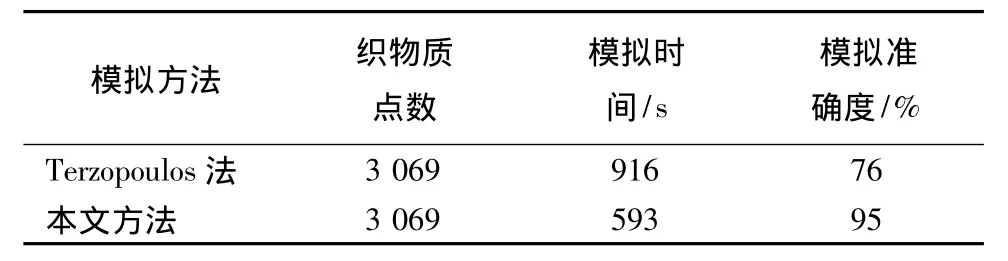
表1 实验结果对比Tab.1 Comparison of two experimental results
5 结束语
本文采用四点插值方法对柔性织物曲面进行模拟,通过分析研究并结合对比实验,得出如下结论。
1)利用四点插值法进行三维织物模拟仿真,不但可方便融合织物的物理特性,而且可利用细分网格的迭代加细特性,动态改变模拟初始网格密度,提高了模拟的真实感。
2)采用四点插值法构造边界点,分析曲面间的光滑拼接条件,实现了不同曲面间的光滑拼接,较好地解决了三维服装模拟中复杂衣片间的缝合问题。
[1] TERZOPOULOS D, FLEISCHER K. Deformable Models[J].The Visual Computer,1988,4(6):306 -331.
[2] BREEN D E,HOUSE D H,WOZNY M J.A Particlebased model for simulating the draping behavior of woven cloth[J].Textile Research Journal,1994,64(11):663-685.
[3] TERZOPOULOS D,HONG Q.Dynamic NURBS with geometric constraints for interactive scalpting[J].ACM Transcations on Graphics,1994,13(2):103 -136.
[4] CHENG C Y,SHI J Y,XU Y Q,et al.Physically based model for real-time animation of curtain movement[J].Journal of Software,2000,11(9):1228 -1236.
[5] FERGUSON J C.Multivariable curve interpolation[J].Journal of the Association for Computing Machinery,1964,11(2):221-228.
[6] COONS S A.Surfaces for Computer-aided Design of Space Figures[M].M I T MAC-M-255,1964:38 -55.
[7] VERSPRILLE K J.Computer-aided design applications of the rationalb-spline approximation form[D].Syracuse N Y:Syracuse Uni,1975:65 -78.
[8] DOROSE T, KASSM, TRUONG T. Subdivision surfaces in character animation[C]//Computer Graphics Proceedings,Annual Conference Series.Orlando:ACM SIGGRAPH,1998:85-96.
[9] DYN N,LEVIN D,GREGORY J A.A 4-point interpolatory subdivision scheme for curve design[J].Computer Aided Design,1987,4:257-268.
[10] KOBBELT L, Interpolatory subdivision on open quadrilateral nets with arbitrary topology[J].Computer Graphics Forum,1996,5(3):409-420.
[11] 梁景鸿.离散的曲线曲面造型方法的应用研究[D].广州:华南理工大学,2002:35-76 LIANG Jinghong.Research on application of discrete curve and surface modeling method[D].Guangzhou:South China University of Technology,2002:35-76.
Study on simulation of flexible fabric bend surface based on four-point interpolation method
YANG Xiaobo
(Dongfang College,Zhejiang University of Finance & Economics,Hangzhou,Zhejiang 310012,China)
In order to further improve the simulation of flexible fabric,a method for simulation of flexible fabric surface based on four-point interpolation is proposed in this paper.The specific research process is as follows.Firstly,analyzing the fabric surface model based on four-point interpolation method,then,using four-point interpolation method to subdivide the curves and surfaces of flexible fabric,finally,performing surface splicing and local modification by the four-point interpolation method,and using comparative experiments to verify the feasibility of the four-point interpolation method.The result shows that the method based on four-point interpolation to simulate true flexible fabric is proposed in this paper,has the simulation accuracy up to above 95%,thereby verifying the feasibility of the method.
four-point interpolation method;flexible fabric;bend surface model;physical simulation
TP 311.131
A
10.13475/j.fzxb.20140404605
2014-04-16
2014-12-04
浙江省自然科学基金资助项目(Y1110023)
杨晓波(1971—),男,副教授,博士。研究方向为纺织材料的计算机视觉分析与模式识别。E-mail:yxb71520@163.com。
