基于小波的无纺布疵点实时检测算法研究

花良浩，陶涛

（扬州工业职业技术学院，江苏扬州，225127）



基于小波的无纺布疵点实时检测算法研究

花良浩，陶涛

（扬州工业职业技术学院，江苏扬州，225127）

［摘要］针对实验项目所使用的薄型用无纺布传统的疵点检测技术主要依靠人为的主观检测问题，提出基于小波的机器视觉的无纺布疵点检测技术，通过分析各种疵点在频域上的特性，采用具有多分辨率特性的小波算法检测疵点，实验可以检测出非常小的孔洞以及杂质型疵点，结果表明，基于小波的无纺布疵点实时检测算法对于毫米级大小直径的杂质型疵点检测效果明显，极大提升了检测速度和准确性。

［关键词］无纺布疵点；小波；准确率；实时性

Research on the Real-time Detection Algorithm of Non-woven Fabric Defect Based on Wavelet

HUA Liang-Hao ,TAO tao
(Yangzhou Polytechnic Institute, Yangzhou 225127, Jiangsu)

［Abstract］In order to solve the problem of the human subjective detection problem on the experiment project by use of thin with non-woven fabric defect detection of traditional technology, we propose a wavelet of non-woven fabric defect detection on machine vision technology. Through the analysis of the characteristics of all kinds of defects in the frequency domain, the multi-resolution characteristics of wavelet algorithm detect defects and the experiment can detect very small holes and impurity defects. The results showed that the non-woven fabric defect real-time detection algorithm based on wavelet for millimeter size of the diameter of the impurity type defect detection effect is obvious, and greatly improve the detection speed and accuracy.

［Key words］non-woven fabric defect, wavelet, accuracy, real-time performance

1　引言

疵点检测技术是无纺布生产过程中的一个重要环节。无纺布疵点检测包括孔洞、异物、折痕等，其评定结果容易受检验人员的主观因素影响，极易出现不客观的评判。传统的疵点检测技术主要依靠人为的主观检测，由于非织造布生产速度及工艺的不断提高，布料产量大幅增长，并且对产品外观质量的要求也越来越高[1]，由于人工检测具有不可避免的缺陷，如人眼容易对微小的疵点漏检、错检，且容易疲劳，检测效率不高等问题，因此，如何快速、准确地检测出非织造布布面疵点，成为当今织造行业一个重要问题。

在无纺布疵点检测方面，国内外学者进行了大量的科学研究。2000年，天津科技大学学者开发了能够在线检测无纺布材料的厚度均匀性的疵点检测系统。该系统主要涉及到非织造材料厚度检测装置和扫描探针传动控制系统、计算机监控系统等[2]。2008年，国立台湾科技大学C. C. Huang等利用小波变换和神经网络方法鉴定无纺布的九种疵点[3]。无纺布样本包括利用水刺法工艺技术，针刺法工艺技术和热熔粘合法工艺技术制成的材料。在对图像去噪后，进行一层小波分解，提取四个子区域的灰度共生矩阵的特征值，以及小波系数的能量值作为纹理特征来训练和测试的神经网络，对于限定疵点检测达到百分之百，但对于复杂种类的疵点检测还不够完善[4-13]。

本文采用实际工业生产，对算法实时性要求极高。为了改善空间域算法的不足，通过分析各种疵点在频域上的特性，发现不同类型疵点在不同频段上特点各不相同，采用具有多分辨率特性的小波算法检测疵点，保证了检测的准确率和实时性。

2　多分辨率分析与小波变换数学意义

对于一个瞬变信号，在不同的局域位置可能含有不同细节程度的频率信息，在某些位置上由于变化剧烈，可能含有大量的细节信息，因此这些区域需要细致的高分辨率进行分析，而在其他一些位置上，信号平稳，故可能只需要较为粗略的低分辨率分析就足够了。这就是多分辨率分析的思想。

从数学角度来讲，多分辨率是指一个具有特定性质的层层嵌套的子空间序列{Vj}j∈z，这个子空间序列充满整个L2（R）空间。在V0空间内找到一个函数g(t)，其平移函数序列{g(t-k)}k∈z构成V0空间的Riesz基，对g (t)函数正交化得到的函数成为正交尺度函数φ(t)。尺度函数基φj,k(t)=2-j/2φ(2-jt-k)由尺度函数φ(t)经过平移和缩放完成，其中j为尺度，k为平移参数。当j一定时，k变化使尺度函数覆盖当前尺度下的尺度子空间；当j变化时，则形成不同尺度子空间，且每当增加一个尺度，尺度函数宽度会增加为原来的一倍，幅度减少为原来的。因此，即由低尺度的尺度函数跨越的子空间在低尺度处嵌套在由高尺度跨越的子空间内。尺度空间示意图如图1所示。

图1　尺度空间和小波空间

尺度函数φ(t)并不是小波函数，但小波函数Ψ(t)可以由尺度函数推导出来。小波函数构成的子空间序列称为小波空间。小波空间与尺度空间之间的关系图1所示，其中{Wj}j∈z是Vj关于Vj+1的正交补子空间，即Vj=Vj-1Wj-1，其小波基为。由上可知小波空间是两个相邻尺度空间的差。相邻尺度空间的投影之间的细小差别即为函数f(t)在相应尺度小波空间上的投影，因此小波空间又叫细节空间。

由于小波基和尺度函数均为各空间上的Riesz基，因此任意子空间的展开函数都可以从他们自身的双倍分辨率副本中得到，即从相邻较高分辨率的空间中得到。即尺度函数可表示为：

由于小波空间存在于相邻较高分辨率尺度函数跨越的空间内，所以任何小波函数可表示为平移的双倍分辨率尺度函数的加权和，写成式(2)，其中hΨ为小波函数系数：

尺度向量与小波函数系数关系：

而任意信号均可分解为小波函数和尺度函数的展开，其离散形式为：

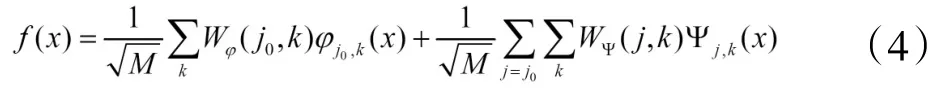
其中，卷积在n=2k时进行计算。在非负偶数时刻计算卷积与以2为步长进行滤波和抽样的效果相同。

3　小波变换算法的实现

3.1小波变换代码实现流程

图像的小波分析是二维小波分析，且一般需要进行多次小波变换，二维小波变换代码实现流程如图2所示。

图2　小波变换基本流程

基本流程总的说来就是在每一个分辨率下进行小波变换时，都先逐行进行变换，然后进行列变换。其中，奇偶分离以6×6数组为例，在图3中分别演示了行变换下的奇偶分离运算以及列变化下的奇偶分离运算，简单说来就是将偶数行或列集中到图像前一半，奇数行或列集中到图像的后半部分。

图3　奇偶分离过程

提升小波变换每执行一次for循环均经过四个步骤。以N×N（其中N为偶数）个像素的图片为例，行变换时，当行数值y（其中y=0,1,2…,N）一定时，提升小波变换第一步将变换（y,N/2）—（y,N-2）这些像素，其中：

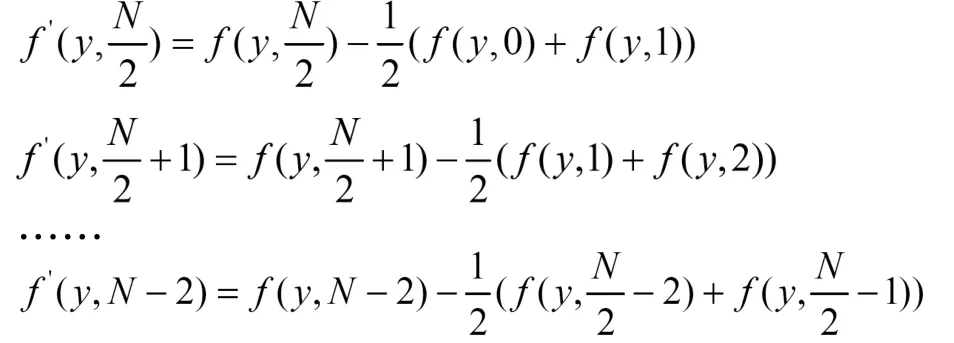
第二步变换(y,N-1)这个像素的值：

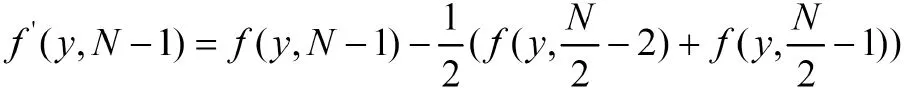
第三步变换(y,0)这个像素的值：

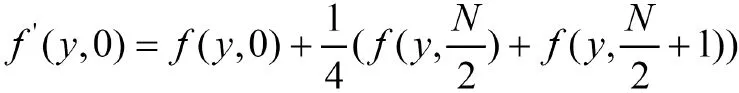
第四步将变换(y,1)—(y,N/2-1)这些像素的值，其中：

经过以上几个步骤之后，便完成了一次提升小波行变换，小波提升行变换总变换次数等于行数y的值。提升小波列变换与行变换相似，在列数x一定情况下，依次变换该列(N/2,x)—(N-2,x)、(N-1,x)、(0,x)、(1, x)—(N/2-1,x)这些像素的值，公式形式不变。

3.2小波变换结果与分析

小波变换只是一个变换工具，将图片从空间域变换到小波域，其作用是突出图像在某个分辨率下、不同方向上的、难以在空间域或傅里叶变换域中观察到的高频特性，而不是像其他算法那样直接分割出疵点。故真正分割出疵点的工作，要在小波变换后，针对所观察到的特点进行有针对性的处理。

图4和5为4096×4096个像素的图片进行两次小波变换的结果。根据这些结果来分析其小波域上的频率特性，为下一步的提取疵点算法的研究打下基础。

图4　原始图像及小波变换之后的低频近似图像

图5　两次小波变换结果图

由图4可以看出，经过两次小波变换之后，低频近似图片变明亮且面积为原图的八分之一，最显著的结果就是深色疵点变得明显。由图5的b和c可以看出，高频结果仅仅保留了折痕疵点，且十分明显。由此可以看出经过小波变换之后，对深色小疵点和浅色较大的疵点均有加强效果，并抑制了背景纹理能量，且将两种疵点在频率域上区分开来。这便使得在空间域上难以检测到的十分小的深色疵点有了被检测出的可能性。

3.3小波域上的疵点检测

由2.2节可知，通过小波变换将孔洞类小疵点和折痕类较大疵点在频域上区分开来：低频近似区域同时包含有孔洞和折痕，且孔洞疵点能量加强变得明显并抑制了背景纹理能量；垂直和竖直方向的高频区域中仅含折痕型疵点不含孔洞型疵点能量，因此可以做如下假设。

猜想一:仅用垂直和竖直方向的高频信息检测折痕疵点；用低频近似区域检测孔洞类小型疵点；

猜想二:虽然低频区域两种疵点并存，如果削弱折痕型疵点在低频区域的能量，孔洞型疵点应更容易被检测出来；

猜想三:竖直和垂直方向均只存在折痕型疵点，如果将这两个区域内能量叠加，折痕能量应变得更大，更容易被检测出来。

遵循以上几个假设，小波变换后，其中，HL与LH相加处理是为了实现猜想三增强高频区域折痕能量；将LL于sum图像相减是为了实现猜想二尽量减少折痕和背景纹理在低频区域上的能量，突出孔洞类型疵点能量：因为图像sum所包含的是该分辨率下的高频信息，即只含有折痕类疵点能量，而LL是近似图像，它既包含低频信息也有高频信息，只不过相对于原始图像而言，其低频信息由于小波变换得到了增强，在LL中去除了高频信息，理论上可以使孔洞类所处的频段能量所占比例进一步提升。

图6　小波域上疵点检测算法

检测结果如图7所示。左上角为原始图像，右上角为LH和HL相加图像，左下角为LL与sum相减图像结果，右下角为图像相减之后的二值化结果。

图7　检测结果

由图7可以看出，经过相减处理后，孔洞类疵点变成灰度级远高于背景和折痕类疵点的较为明显的高灰度级对象，这为下一步的二值化提供了良好的基础——只需设定一个较高的阈值，便可以将孔洞类疵点提取出来，无论疵点再小都可以实现其提取操作。图7(b)可以看出求和之后折痕能量相较于图5中b和c而言有大幅的提升，变得十分明显，折痕提取轮廓结果以及与差图像融合之后的最终结果如图8所示。

图8　轮廓提取结果以及最终结果

由图8(b)可以看出，在空间域上检测不出来的非常小的孔洞、杂质型疵点，在小波域上可以很好地提取出来。

4　基于小波疵点算法的实时性分析

对于本项目而言，好的检测算法需要达到两个要求：一是准确性；二是实时性。本文针对本项目所研究的算法准确性较高，但是实时性还需进一步的验证。

本项目硬件环境为Pentium (R) Dual-Core CPU，主频2.00GHz，内存4GB；软件环境为Windows7 32位操作系统，实验平台为vs2008集成开发环境。在对4096×4096大小的图片进行两次小波变换的情况下，整个算法用时为8.4s左右。这个速度对比实验室以前用Gabor小波进行计算的速度快了很多，Gabor检测同样大小的图片，由于疵点非常小，为了保证结果准确性必须进行高精度计算，整个算法用时约为145.57s左右。具体统计结果见表1。

表1　不同图像大小情况下小波算法与Gabor算法的比较

由上表可以看出，基于小波的算法比之前的算法速度快,对于项目实际需求而言，达到实时检测的目的，提升了算法速度。

5　小结

本文阐述了多分辨率分析以及小波变换的原理和在图像处理中的意义，给出了基于小波变换的疵点检测算法的实现步骤及其结果，发现基于小波的疵点检测算法能够较好的检测出空间域内无法检测出的孔洞、异物类型疵点。最后分析了该算法的实时性，与实验室以往的算法进行比较，由结果可以看出，该算法计算速度有了很大提高。

[参考文献]

[1]刘曼曼,廖康,廖小龙,等.无纺布果袋内微环境特征及其对库尔勒香梨果实品质的影响[J].经济林研究,2014,32(2):83-87.

[2]杨云.基于机器视觉的非织造材料厚度均匀性检测系统的研究[D].武汉纺织大学,2011.

[3]刘建立.基于小波分析和BP神经网络的织物疵点识别[D].苏州大学,2008.

[4]徐秀秀,梁久祯.基于小波和流形学习的人脸姿态表情分析[J].计算机应用与软件,2015,32(3):167-171,176

[5]赵祖轩.基于Contourlet变换和子空间分析的人脸识别技术研究[D].北京化工大学, 2010.

[6]刘涛.小波变换技术概述[J].中国新技术新产品,2010,1(22): 33-38.

[7]黎林,朱军.基于小波分析与神经网络的语音端点检测研究[J].电子测量与仪器学报,2013,27(6):528-534.

[8]夏加星.医学图像融合方法研究[D].江苏科技大学,2012.

[9]周怡,吴雷.基于p-q-r法的小波分析谐波检测算法[J].电力电子技术,2013,47(1):92-94.

[10]Genitsaris S, Kormas K A, Christaki U. Molecular diversity reveals previously undetected air-dispersed protist colonists in a Mediterranean area[J]. Sci Total Environ, 2014,478C:70-79.

[11]李致远,朱求志,焜吴永,等.基于小波分析的无线传感网实时异常检测算法[J].南京师大学报,2014,37(1):87-92.

[12]曹瑜,涂玲,毋立芳.身份认证中灰度共生矩阵和小波分析的活体人脸检测算法[J].信号处理,2014,30(7):830-835.

[13]李修文,阳建宏,黎敏,徐金梧.基于移频技术的短时傅里叶变换阶比分析[J].北京科技大学学报,2012,34(10):1190-1196.

［作者简介］花良浩（1989-），男，江苏盐城人，扬州工业职业技术学院，研究方向：检测技术与自动化装置、故障诊断技术。

［基金项目］中央财政支持的职业教育实训基地建设项目（苏教财[2012]117号）；2015年江苏省大学生实践创新训练计划项目（项目编号：201513754004Y）。

［收稿日期］2015-10-12

［中图分类号］TS107

［文献标识码］A

［文章编号］1671-5004（2015）06-0001-03