纤维在研磨流场区域流动状况的数值模拟1)
2015-03-10花军陈光伟刘龙许威
花军 陈光伟 刘龙 许威
(东北林业大学,哈尔滨,150040)
纤维在研磨流场区域流动状况的数值模拟1)
花军 陈光伟 刘龙 许威
(东北林业大学,哈尔滨,150040)
根据纤维的流动特性及热磨机实际工况下的压力参数和设定的动磨片转速,选择一对动/静磨片;将由动/静磨片和磨片间隙组成的研磨流场区域,划分为3个域,对纤维在研磨流场区域中的流动状况进行了数值模拟研究。结果表明:纤维在研磨流场区域中的压力、速度、剪切应力分布,与实际工况中磨片的磨损状况相符;3种参数分布相互关联,符合流体力学的运动规律。
纤维;研磨流场;流动状况;数值模拟
经热磨机磨片研磨分离的单体纤维,在天然有机化学中属于长链高分子聚合物。大量纤维在热磨机磨片动盘旋转的带动下发生流动,从纤维总体流动模式看,纤维拥有流体的流动性、连续性和黏度等基本属性,流体力学对植物纤维有其定义,属于非牛顿流体范畴中的宾汉流体[1-4]。国内外学者,在将流体力学理论引入纤维分离过程研究领域,已取得了很大的进展[5-7],如:芬兰美卓公司,采用“电脑纤维流化”技术优化磨片齿形结构,控制纤维原料的流动,保证原料在解离区最佳的分布方式和恒定的流动;国内陈光伟[8-9]、徐大鹏[10]等,基于流体力学理论对纤维分离过程进行了数学建模,推导出了纤维的受力状态和运动轨迹的公式,并计算了纤维流体的黏度和雷诺数等重要参数;朱小林[11]等,对热分散机内部浆料的湍流流动,从二维的角度进行了计算流体力学仿真,深入分析了盘式热分散机理和影响因素。
热磨机研磨纤维时,磨片内部流场纤维原料的瞬时运动参数(速度、压力、运动轨迹或壁面剪切应力等),无论从实际生产工况和实验角度均无法测得;用计算流体力学方法数值模拟纤维分离过程,以掌握上述瞬时参数的分布,有助于深入研究纤维分离理论,提高我国磨片理论设计水平,对纤维板生产企业提高纤维质量,均有着重要理论和实际应用价值。
1 流场物理模型的建立
本模拟的对象是一组磨片所构成的磨盘,流场所在区域,即动、静磨盘之间所夹的狭窄空间。纤维原料在热磨机磨片研磨区时的形态,多以纤维束和纤维形态运动,此数值模拟只针对研磨区,以便数值模拟更接近实际工况。
流场物理模型的建立如图1所示。其中:图1a是构成模拟流场的动/静磨盘之一(动/静磨片齿形相同),图中指出了纤维原料的入口和研磨完成时纤维的出口,箭头指向的是纤维流动方向,纤维原料从破碎区流向粗磨区而后流向精磨区;图1b带有周向齿的研磨区域属于精磨区,剩余的是粗磨区;模型统称为研磨区模拟模型。图中磨片结构是带有相似性、周期性排列等规则,因此,利用数值模拟软件周期性网格的技巧,只计算全磨盘的1/104,可减少大量计算时间。
2 流场的基本假设及边界条件的设定
为了将问题简化和突出研究重点,对纤维在研磨流场区域内运动状态的数值模拟做出如下假设:①动、静磨盘内部流场中,纤维原料被视作不可压缩流体;②纤维原料与动、静磨盘内壁间无相对滑动;③旋转过程中,不考虑动、静磨盘及壳体的热变形与热传导;④纤维原料的物性参数为常数;⑤入口纤维原料流速均匀。

图1 研磨区模拟模型示意图
本模拟属于旋转流动问题,随着时间的推移,纤维流体的流动状态发生着不断的改变,即非定常问题。在纤维运动模拟流场中,需要设定的边界条件,有进口边界条件、出口边界条件、固壁边界条件、内部边界条件、周期性边界条件。纤维流体运动黏度取0.992 Pa·s;常用木材密度范围为400~750 kg/m3,取500 kg/m3。
进口条件:设定为纤维原料的进口压力,此值为长时间检测实际工况下蒸煮罐压力并求得的平均数,设定为0.88 MPa。
出口条件:设定为纤维原料的出口压力,此值为长时间检测实际工况下热磨机压力并求得的平均数,设定为0.82 MPa。
动、精磨片侧壁的处理:动/静磨齿、动/静磨片内壁,设置成固体壁面,壁面流动边界设置为无滑移固壁条件。
内部边界处理:将计算区域划分为动磨片区域、磨片间隙和静磨片区域,它们之间以数据交换面加以分开,两区域之间的数据通过数据交换面交换。
周期性边界:设置为旋转式周期性边界条件。
3 模拟结果与分析
3.1 模型压力分布
纤维原料流经动磨片破碎区与粗磨区过渡区域,以及粗磨区与精磨区过渡区域的压力,由最大逐渐变小(见图2)。这主要是由于,从粗磨区向精磨区过渡,齿槽宽度减小,类似流体力学中的流体从通流截面较大位置流向较小位置的模型;流体经过过渡区域时,需要压力梯度的驱动,因此在过渡区域承受压力由大逐渐变小。相临的齿槽中的压力分布是基本相同的,而且越向模型x轴正方向延伸;压力越小,根据伯努利方程,压力能转化为动能,压力降低。

图2 动磨片压力分布(单位:Pa)
纤维原料流经静磨片破碎区与粗磨区过渡区域,以及粗磨区与精磨区过渡区域的压力分布规律,与动磨片的压力分布基本相同(见图3)。

图3 静磨片压力分布(单位:Pa)
纤维原料流经磨片间隙域,磨片间隙的压力分布如图4所示。在磨片间隙区域,压力分布相差较大:最小压力为0.71 MPa,出现在磨齿正对位置之下;最大压力为1.05 MPa,出现在磨片旋转方向的一侧;0.7~1.2 MPa,属于热磨机研磨压力的正常范围;在齿槽下的大部分范围内,磨片间隙的压力,是沿x轴正方向逐渐减小的趋势,但压力相差不大。
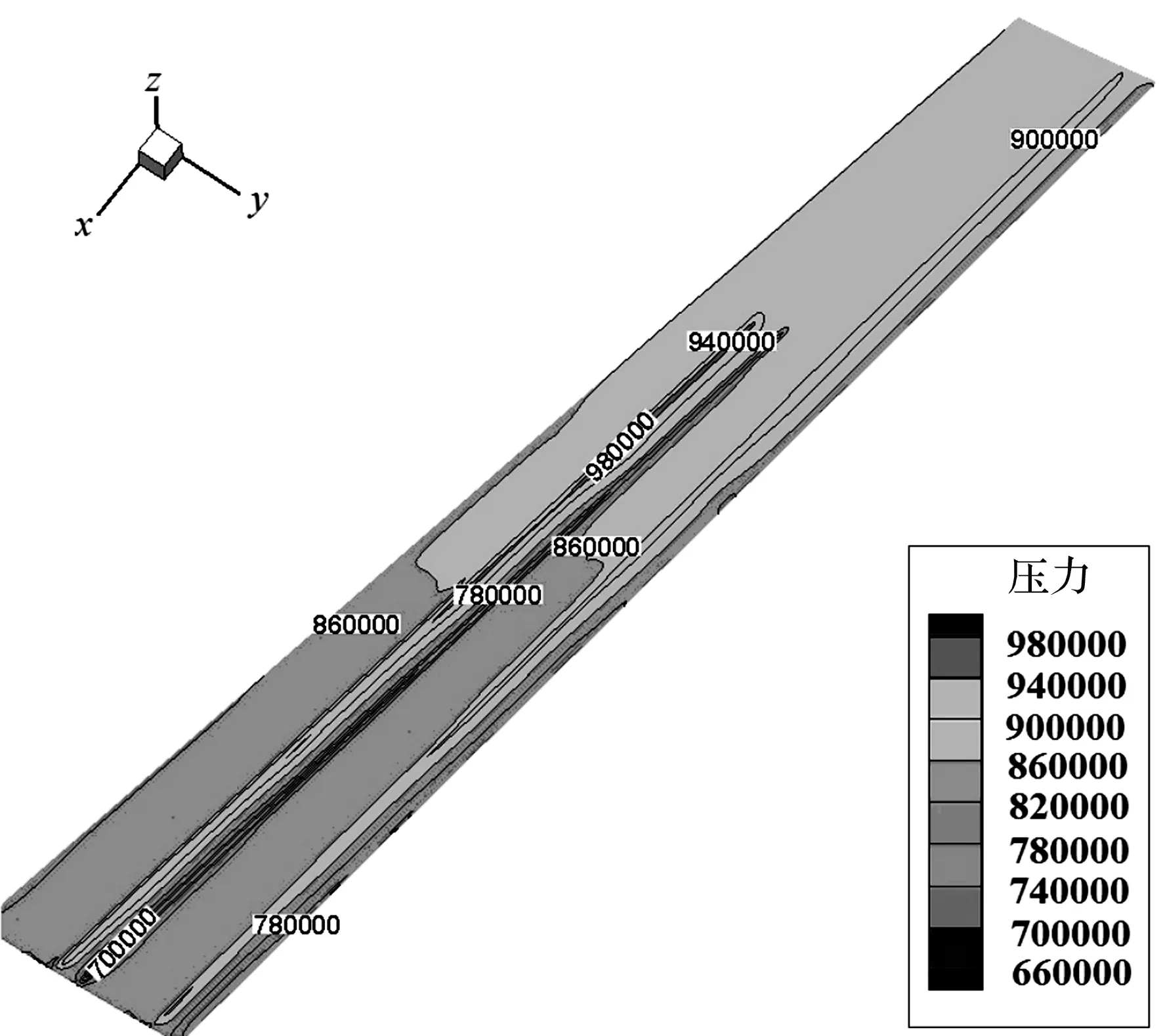
图4 磨片间隙压力分布(单位:Pa)
比较图2至图4,模拟模型的压力分布规律,都是沿x轴正方向压力逐渐减小,且在粗磨区到精磨区的过渡区域的压力最大。这在实际工况下,失效磨片得以体现;磨片粗磨区到精磨区的过渡区域,磨损程度最大(见图5中圈内部分)。

图5 失效磨片磨损情况
通过进一步分析磨片间隙压力分布(见图4)、动磨片压力分布切片(见图6)、静磨片压力分布切片(见图7)(切片方向如图2中箭头方向所示,垂直于x轴,平行于yoz面,下文切片方法与此处相同),在动磨齿经过的位置,会出现最大的压力。在图6中,动磨片旋转方向是逆时针的,最前切片磨齿的右下角压力最大,该位置是动磨片磨齿起切割、研磨作用的齿刃;而在图7中,最前切片磨齿的左上角齿刃压力也最大。所以,这2个位置,在实际工况中,磨片磨齿齿刃的一侧磨损程度较另一侧大得多,图5验证了本模拟的有效性。

图6 动磨片压力分布切片(单位:Pa)

图7 静磨片压力分布切片(单位:Pa)
3.2 模型速度分布
纤维流体在动磨片中的运动速度,规律性很强,沿x轴正方向速度逐渐增大。这是由于,压力能克服了摩擦力,转化了流体的动能,所以沿x轴正方向,压力大小和速度大小变化趋势是相反的(见图8)。对比动磨片压力分布(见图2)和动磨片速度分布(见图8),可看出:在过渡区域,粗磨区的压力大、速度小;进入精磨区域时,压力变小、速度变大;这符合流体力学质量守恒定律。对于不可压缩流动,进口面积与进口速度的乘积,等于出口面积与出口速度的乘积,因此,进口速度较慢,出口速度较快。
纤维流体在齿槽流动过程中,运动方向是沿着动磨片旋转方向的,即逆时针,且基本是垂直于磨齿的;在动磨片的齿槽中,存在速度梯度,从磨片间隙到磨片齿槽底部,纤维流体的运动速度逐渐增大(见图9)。
分析可知,纤维流体在磨片间隙中运动速度的分布规律(见图10、图11)。纤维流体在磨齿下的运动速度较小,且流体速度大小大致相同;在齿槽间流动速度,相对磨齿下流动速度较大,沿x轴正方向,速度主要呈逐渐增大趋势,接近出口时达到最大。由于纤维流体本身的高黏性,在动磨盘高速旋转的带动下,其运动方向与磨片磨齿夹角大于90°,向着模型出口呈扩散状运动。

图8 动磨片速度分布(单位:m/s)

图9 动磨片速度分布切片(单位:m/s)
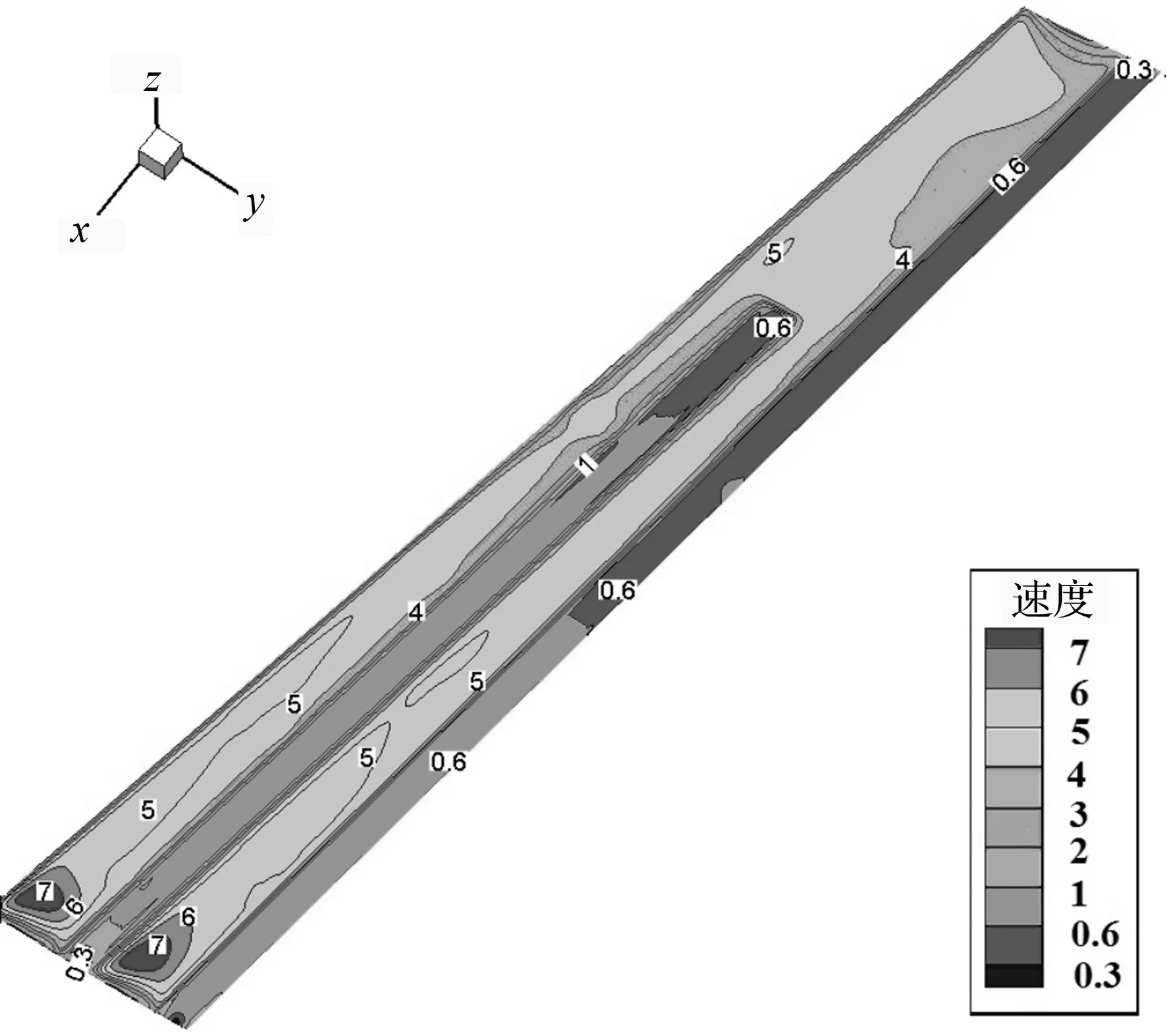
图10 磨片间隙速度分布(单位:m/s)

(a)过渡区域流体矢量;(b)出口区域流体矢量。
纤维原料在静磨片的速度,是从小逐渐增大的变化趋势(见图12)。在最贴近磨片间隙的一层,沿x轴正方向,纤维流体速度的变化趋势,与磨片间隙速度分布大致相同。
通过静磨片模型切片分析可知,纤维流体在静磨片中运动,同样也存在速度梯度;从磨片间隙到磨齿齿槽底部方向,速度逐渐减小,而且磨齿齿槽底部,大部分纤维原料保持着相当低的速度流动着(见图13)。纤维流体在静磨盘中的运动轨迹,是沿着磨片齿槽方向的漩涡的产生,会导致流体产生与磨片转向相反的力矩;因而热磨机实际的能量转换过程会发生能量损耗,即磨片动能与浆料压力能之间,实际发生的能量转化小于理想条件下的能量转化。比较动磨片、磨片间隙、静磨片中纤维流体的流动规律:和动磨片接触的纤维层与磨片同步旋转速度最大,和静磨片接触的纤维层速度最小,两层之间的磨片间隙速度居于其间。速度方向,是动磨片中纤维与磨片旋转速度的切线方向,基本与磨齿垂直;磨片间隙中的纤维,由于其本身的高黏性,在动磨盘高速旋转的带动下,其运动方向与磨片磨齿夹角大于90°,向着模型出口呈扩散状运动;静磨片中纤维,由于在静磨区齿槽内和磨片间隙中,流体流速与静磨片中不对称,产生压力梯度,诱发漩涡,而且是纤维沿着磨片齿槽方向的漩涡运动。

图12 静磨片速度分布(单位:m/s)

图13 静磨片速度分布切片(单位:m/s)

图14 静磨片速度分布、运动轨迹切片(单位:m/s)
3.3 模型剪切应力分布
在磨片间隙速度分布中(见图10),在磨片磨齿对应下方的磨片间隙区域内,有着较密集的黑色等值线,说明速度有着很大程度的降低,在很小的范围内有着较大速度梯度存在。可以推断出,在动磨片齿刃附近会有很大的剪切率,即会有很大的剪切应力存在(在黏性流体力学中,剪切应力等于液体剪切黏度与剪切率之积,速度梯度又称剪切率)。
从磨片间隙对应齿刃壁面剪切应力(图15)可见,颜色最深的区域是动磨片磨齿齿刃,越靠近齿刃壁面处的,剪切应力越大;越靠近出口位置齿刃的,剪切应力也越大;磨片粗磨区的壁面剪切应力,小于精磨区的壁面剪切应力,原因是,在粗磨区,纤维流体流动速度的变化梯度,小于精磨区区域;周向齿处剪切应力很小,原因是,周向齿在实际工况中,主要作为挡坝作用,防止纤维原料快速流出磨盘。
从动磨片壁面剪切应力分布(图16)可见,模型出口处的壁面,有着较大的剪切应力。原因是,纤维流体的速度,由粗磨区到精磨区方向逐渐增加,到接近出口处逐渐达到最大速度;由于出口有少量流体回流,这部分纤维流体的速度很小,因此,在很小的范围内有很大的速度梯度(见图8),剪切率很大,产生较大的剪切应力。
从静磨片壁面剪切分布应力(见图17)可见,相对于磨片间隙附近壁面、动磨片壁面,静磨片的壁面剪切应力小的多,尤其在静磨片粗磨区的壁面,剪切应力几乎为零。原因是,纤维流体在静磨片流场区域内的速度本身很小,静磨片流场区域又有漩涡扰流,速度变化很小,没有明显的速度梯度,就没有剪切率。

图15 磨片间隙附近壁面剪切应力分布(单位:Pa)

图16 动磨片壁面剪切应力分布(单位:Pa)
图17 静磨片壁面剪切应力分布(单位:Pa)综合分析,模型流场中剪切应力,从大到小依次为:磨片间隙中剪切率、动磨片齿槽内剪切率、静磨片齿槽内剪切率。这也进一步表明,在热磨机中,体积较小的纤维解离、研磨,主要发生在磨片间隙中;体积较大的纤维原料,在动磨片齿槽内的分离效果,好于在静磨片齿槽内的分离效果。
4 结论
模拟模型的压力分布规律:沿x轴正方向逐渐减小,且在粗磨区到精磨区的过渡区域内,压力由最大逐渐变小。在实际工况下,失效磨片粗磨区到精磨区的过渡区域,磨损程度得以体现,验证了本数值模拟的有效性。
模拟模型的速度分布规律:和动磨片接触的纤维层与磨片同步旋转速度最大,和静磨片接触的纤维层速度最小,2层之间的磨片间隙速度居于其间。模拟模型的速度方向分布规律:动磨片中的纤维与磨片磨齿垂直,磨片间隙中的纤维与磨片磨齿夹角大于90°,静磨片中纤维沿着磨片齿槽方向做漩涡运动。
模拟模型中,流场中的剪切率,从大到小依次为:磨片间隙中的剪切率、动磨片齿槽内的剪切率、静磨片齿槽内的剪切率。剪切应力最大的2个位置:一个是动磨片齿刃处,另一个是模型出口处。在热磨机中,体积较小的纤维解离、研磨,主要发生在磨片间隙中;体积较大的纤维原料,在动磨片齿槽内的分离效果,好于在静磨片齿槽内的分离效果。
研究结果表明:纤维在研磨流场区域中的压力、速度、剪切应力分布,与实际工况中磨片的磨损状况相符,3种参数分布相互关联,符合流体力学的运动规律。这为完善纤维分离理论和磨片齿形结构参数的优化设计,提供了参考。
[1] 陈光伟.热磨法磨片纤维分离机理的模型分析与实验研究[D].哈尔滨:东北林业大学,2012.
[2] 王忠奎.热磨机磨片对中密度纤维板纤维分离质量影响机理的研究[D].哈尔滨:东北林业大学,2003:8-10.
[3] 徐大鹏.MDF纤维分离机理及磨片齿形结构参数优化设计的研究[D].哈尔滨:东北林业大学,2012.
[4] 陈懋章.黏性流体动力学基础[M].北京:高等教育出版社,2002:98-132.
[5] Karlberg M, Aidanpaa J O. Rotordynamical simulations of a fibre refiner during production[J]. Journal of Sound and Vibration,2011,330(18/19):4460-4473.
[6] Karlberg M, Aidanpaa J O. Rotordynamical modeling of fiber refiner during production[J]. Journal of Sound and Vibration,2007,303(3/5):440-454.
[7] Runklera T A, Gerstorferb E, Schlangc M, et al. Modelling and optimization of a refining process for fibre board production[J]. Control Engineering Practice,2003,11(11):1229-1241.
[8] 陈光伟,花军,纪伟,等.磨片结构对纤维分离过程中能量转换机理的影响[J].东北林业大学学报,2010,38(8):109-110,114.
[9] 陈光伟,花军,贾娜,等.影响热磨机磨片齿形结构设计要素分析[J].林业机械与木工设备,2008,36(6):11-13.
[10] 徐大鹏,陈光伟,张绍群,等.纤维分离过程力学模型的建立及其运动状态分析[J].东北林业大学学报,2012,40(1):90-92,96.
[11] 朱小林.胶黏物盘式热分散机理与能耗建模研究[D].广州:华南理工大学,2010:103-105.
[12] 唐家鹏.FLUENT14.0超级学习手册[M].北京:人民邮电出版社,2013.
[13] 孙石,李文姬.FLUENT在动力机械中的应用[J].长春工程学院学报:自然科学版,2010,11(4):46-48.
Numerical Simulation of Fiber Flow Conditions in the Grinding Area
Hua Jun, Chen Guangwei, Liu Long, Xu Wei(Northeast Forestry University, Harbin 150040, P. R. China)/Journal of Northeast Forestry University,2015,43(4):113-118,130.
With the flow characteristics of the fibers, the sum of defibrator actual conditions pressure parameters and the speed of dynamic grinding disc, we selected a pair of dynamic/static disc to divide the abrasive flow field formed by dynamic/static disc and the grinding gap. By the numerical simulation, we studied the fiber in the region of flow condition in the abrasive flow field. The fiber pressure, velocity and shear stress distribution in area of the flow field were in accordance with the actual condition of the grinding wear. Three parameters' distribution correlated with each other, which was consistent with fluid mechanics.
Fiber; Grinding; Flow field; Flow status; Numerical simulation
花军,男,1959年5月生,东北林业大学机电工程学院,教授。E-mail:huajun81@163.com。
2014年10月16日。
TS642
1)教育部高等学校博士学科点专项科研基金(博导类)课题(20130062110005)。
责任编辑:张 玉。
