基于SEM三江平原湿地生态系统健康与扰动因素分析

2015-03-10王书可李顺龙

东北林业大学学报 2015年2期

关键词：三江平原扰动方程

王书可李顺龙

(东北林业大学，哈尔滨，150040)

基于SEM三江平原湿地生态系统健康与扰动因素分析

王书可李顺龙

(东北林业大学，哈尔滨，150040)

依据三江平原湿地生态系统特点，用SPSS20.0和Lisrel8.7软件建立了结构方程模型。根据结构方程模型分析，确定湿地生态系统健康的主要影响因子及其相互关系。结果表明：自然扰动和人类扰动，直接影响湿地自我免疫与抗扰动能力的发挥；湿地自我免疫与抗扰动能力，又影响湿地满足人类社会需求能力，具有中介变量的属性。湿地满足人类社会需求能力，是湿地生态系统健康的直接表现；湿地自我免疫与抗扰动能力，是湿地生态系统健康的间接反映。

三江平原；湿地生态系统；生态系统健康；结构方程模型

On the basis of Sanjiang Plain Wetland ecological system characteristics, we established structural equation model with SPSS20.0 and Lisrel8.7 software. According to the structural equation model analysis, we determined the main factors that influence the wetland ecosystem health and its relationship to each other. Natural disturbance and human disturbance directly affected the wetlands immune and ability to resist disturbance. Wetlands’ immunity and its ability to resist disturbance of self-ability affected the demand of human society, and it possessed the property of the intermediary variable. Wetland ability to meet the demand of human society was the direct expression of wetland ecosystem health, and wetlands’ immunity and its ability to resist disturbance were the indirect reflection of wetland ecosystem health.

三江平原湿地是我国湿地面积最大、集中连片的淡水湿地分布区，是《中国生物多样性保护行动计划》和《中国湿地保护行动计划》列出的优先地区，也是全球及其生物多样性最丰富和关键地区之一，具有重要国际意义；其中洪河、三江、兴凯湖湿地自然保护区，已被列入国际重要湿地名录。三江平原作为我国粮食主产区，兼具商品粮生产基地和战备粮储存基地双重任务，对我国的粮食安全起到稳压器和调节器的重要作用。60 a来，由于人类过度使用自然资源，恣意改变湿地用途，导致生态环境巨变、自然资源丧失。从而引发三江平原湿地面积逐渐减小、湿地生态功能明显下降、生物多样性降低、自然灾害频发、社会经济严重受损等一系列严重的生态危机和社会危机。面对人口与农业压力，变化的自然环境，人才与社会资源的外流。如何合理利用湿地资源；如何在确保粮食安全的同时，保障区域生态环境安全和区域经济的可持续发展，追求最佳综合效益；是该区目前面临的主要社会经济管理问题。

关于生态系统健康的研究，起源于20世纪80年代后期Schaeffer和Rapport的研究。Schaeffer认为，生态系统健康，是指生态系统没有疾病；而生态系统疾病，是指生态系统的组织受到损害或减弱[1]。目前，对于湿地生态系统健康的研究，主要集中于生态技术领域的评价[2]，对于湿地生态系统健康内涵的定义也未形成统一认识。在评价过程中，重视技术，忽视人和社会心理等人文因素。对于湿地生态系统管理的研究，则主要集中于立法、管理体制和政策方面[3]，忽视技术因素。一方面，技术发展与管理变革相互割裂，生态技术的进步并未惠及管理手段更新，在为政府提供决策依据方面欠缺自成体系的理论和有说服力的评价实证[4]；另一方面，技术领域与管理领域，均出现重技术、重自然，忽视人文关怀的趋势，合理利用湿地与保护湿地的临界点不明晰。三江平原湿地生态系统管理的侧重点，从建国初期，如何利用湿地资源转变到如何限制使用湿地资源，影响当地居民的生活。保护湿地、保护自然的根本目的，为人类社会提供和谐发展的空间，满足人类社会生存、繁衍和发展的需要。本文综合自然与人类社会因素，根据崔保山等[1，5]对湿地生态系统健康的界定，将三江平原湿地生态系统健康内涵分类界定；根据调查问卷结果，分析社会认知；通过构建结构方程模型，评定三江平原湿地生态系统健康的主要影响因素。旨在为管理目标的价值取向提供参考。

1 研究区域概况

三江平原位于黑龙江省东北部，北纬45°29′～48°30′，东经130°20′～135°05′。天然湿地，主要分布在沿黑龙江、乌苏里江、松花江，及其支流(挠力河、穆棱河、别拉洪河、阿布沁河、七虎林河、浓江、鸭绿河、楼肯河、嘟噜河、安邦河等)的河漫滩、古河道、阶地上低洼地各类湖泊(如大小兴凯湖、东北泡、大力加湖等)和湖滨洼地。三江平原湿地类型有4种，即河流湿地、湖泊湿地、沼泽、沼泽化草甸湿地及库塘，分别为1.24×105、2.04×105、1.159×106、2.97×104km2[5]。湿地总面积为1.518×106hm2，占三江平原地区总面积的13.95%，占全国湿地总面积的36%；其中，沼泽和沼泽化草甸湿地占三江平原湿地总面积的76.38%[6]。

2 结构方程模型

2.1 理论模型的构建

湿地生态系统健康，是生态系统没有疾病[1]，系统内关键生态组分和有机组织保存完整，既可以自我持续发展，又具有功能整合性[7]，包括“湿地自我免疫与抗扰动能力”和“湿地满足人类社会需求能力”。湿地生态系统无时无刻都受到扰动，是一种不可避免的现象，直接影响着湿地生态系统健康及生态系统的形成、发育和演变过程。扰动分为自然扰动和人类扰动，同时对湿地生态系统健康产生影响，因此可以得出湿地生态系统健康与扰动因素的理论模型(见图1)。由图1可见：无论自然扰动，还是人类扰动，都属于外生潜变量，湿地生态系统健康属于内生潜变量。

图1 湿地生态系统健康与扰动因素的理论模型

根据湿地生态系统健康的内涵，可将其分解为2个潜变量，即：“湿地自我免疫与抗扰动能力”和“湿地满足人类社会需求能力”，属于内生潜变量。“湿地满足人类社会需求能力”是“湿地自我免疫与抗扰动能力”的目标，“湿地自我免疫与抗扰动能力”是“湿地满足人类社会需求能力”的前提和基础；所以，“湿地自我免疫与抗扰动能力”影响“湿地满足人类社会需求能力”。由此，可以推导出湿地生态系统健康与扰动因素的因果模型(见图2)。

根据湿地生态系统健康内涵和理论模型，提出总假设：扰动(扰动的健康性)对于三江平原湿地生态系统健康具有直接的正效应。根据总假设和图2中的因果关系，衍生出5项假设：H1——自然扰动，对于湿地自我免疫与抗扰动能力，具有直接正效应；H2——人类扰动，对于湿地自我免疫与抗扰动能力，具有直接正效应；H3——自然扰动，对于湿地满足人类社会需求能力，具有直接正效应；H4——人类扰动，对于湿地满足人类社会需求的能力，具有直接正效应；H5——湿地自我免疫能力与抗扰动能力，对于湿地满足人类社会需求能力，具有正效应。

图2 湿地生态系统健康与扰动因素的因果模型

2.2 探索性因子

探索性因子分析，试图揭示一套相对比较大的变量的内在结构[8]。本文使用SPSS20.0对变量进行信度和效度检验；选取指示度较高的观测变量，提取公共因子；通过因子载荷，推断数据的因子结构。

2.2.1 调查问卷

在问卷衡量工具上，利用评分方式打分。采用李克特5级量表的形式，采用描述性语言为受访者主观感受或评价定级。李克特量表，是评分加总式量表，由美国社会心理学家李克特于1932年在原有的总加量表基础上改进而成[9]。该量表由一组陈述组成，每一陈述有非常同意、同意、不一定、不同意、非常不同意5种回答，分别记为1、2、3、4、5；每个被调查者的态度总分，是他对各道题的回答所得分数的加总，这一总分可说明他的态度强弱或他在这一量表上的不同状态。

本文的调查问卷，主要回答以下4方面的问题：对于三江平原湿地生态系统自然扰动因素、人类扰动因素、三江平原湿地自我免疫与抗扰动能力、湿地满足人类社会需求能力的评价如何。根据研究的需要和可操作性要求，本文以三江平原地区行政区划中市县的湿地自然保护区的管理者及当地居民为调查对象，采访区域包括依兰县、汤原县、抚远县、富锦市、双鸭山市宝清县。本课题的调研，共计发放调查问卷300份，调研结束后共回收问卷263份；经统计后，有效的调查问卷为224份，所占比例为88%。调查过程中，调查涉及变量最大值为5，最小值为1。关于调查的问题，接受调查的人员，对每个问题只有一项最满意，其他指标都不存在最满意的情况。调查问卷有一定的普遍性，说明对于三江平原湿地生态系统健康及扰动因素还具有提升的空降，说明预期与现实还存在较大差距，需要全面改进和提升。

2.2.2 信度检验

信度指测量数据结果的可靠性，意义是指测量值的一致性和稳定性程度[10]。一份可靠性高的调查问卷，其信度系数应在0.8以上。统计计算过程中，本文用基于Cronbach’sα的方法进行变量信度分析；通过项总计相关系数(CITC)，对涉及问题的单个指标进行可靠性分析。在常规统计分析中，CITC系数一般要求在0.5以上；假如出现单个指标的CITC小于0.5，而另一方面，总量统计表中的CITC在0.6以下，说明该项分析的指标要进行必要的修改或删除。

使用SPSS20.0，对“湿地自我免疫与抗扰动能力”、“湿地满足人类社会需求能力”、“自然扰动”、“人类扰动”4个潜变量进行信度分析，得出4个潜变量的Cronbach’sα系数值，分别为0.892、0.922、0.736、0.731，均满足大于0.7的标准，说明变量内部具有相当的信度。由表1可见：除了NS2、NS4的校正的项，总相关性的系数值小于0.5，其他选项的系数均大于0.5，可以将此2项剔除；除了RN3的校正的项，总相关性的系数值小于0.5，其他选项的系数均大于0.5，可以将此项剔除。调查问卷总共有20个观测变量，使用SPSS20.0进行信度分析，得出Cronbach’sα系数为0.907。

2.2.3 效度检验

效度是指研究得到的测量值和真实值的接近程度[10]。调查问卷的KMO(Kaiser Meyer Olkin)和Barlett检验，取样足够度的KMO度量为0.829(验证值)、Bartlett的球形度检验近似χ2为3 842.773、df为120、Sig为0。结合KMO的取值范围解释(见表2)，可以得出，该项统计检验的结果科学合理，可以作为因子分析检测；同时，也说明可以对该项指标的因子进行分析，而且能够应用模型假设进行验证研究。由表3可见：通过引入主成分分析法，结果归结到4个公共因子(主成分)，而且经计算得出其累计方差的共效率达到了80.777%。由表4可见：经过旋转，在5次迭代后，各观测变量只在一个公共因子上有较大的因子载荷，提取RN1、RN2从属于第4个公共因子，RH1、RH2、RH3从属于第3个公共因子，HS1、HS3、HS5、HS6、HS7、HS8从属于第2个公共因子，NS1、NS2、NS3、NS4、NS5从属于第1个公共因子。这种从属关系，是变量的内部因子结构。探索性因子分析，致力于找出事物内在的本质结构[8]，因此，以上揭示观测变量与公共因子的从属关系的过程，也是探索性因子分析的过程；从数据中寻找因子结构，验证我们的假设。

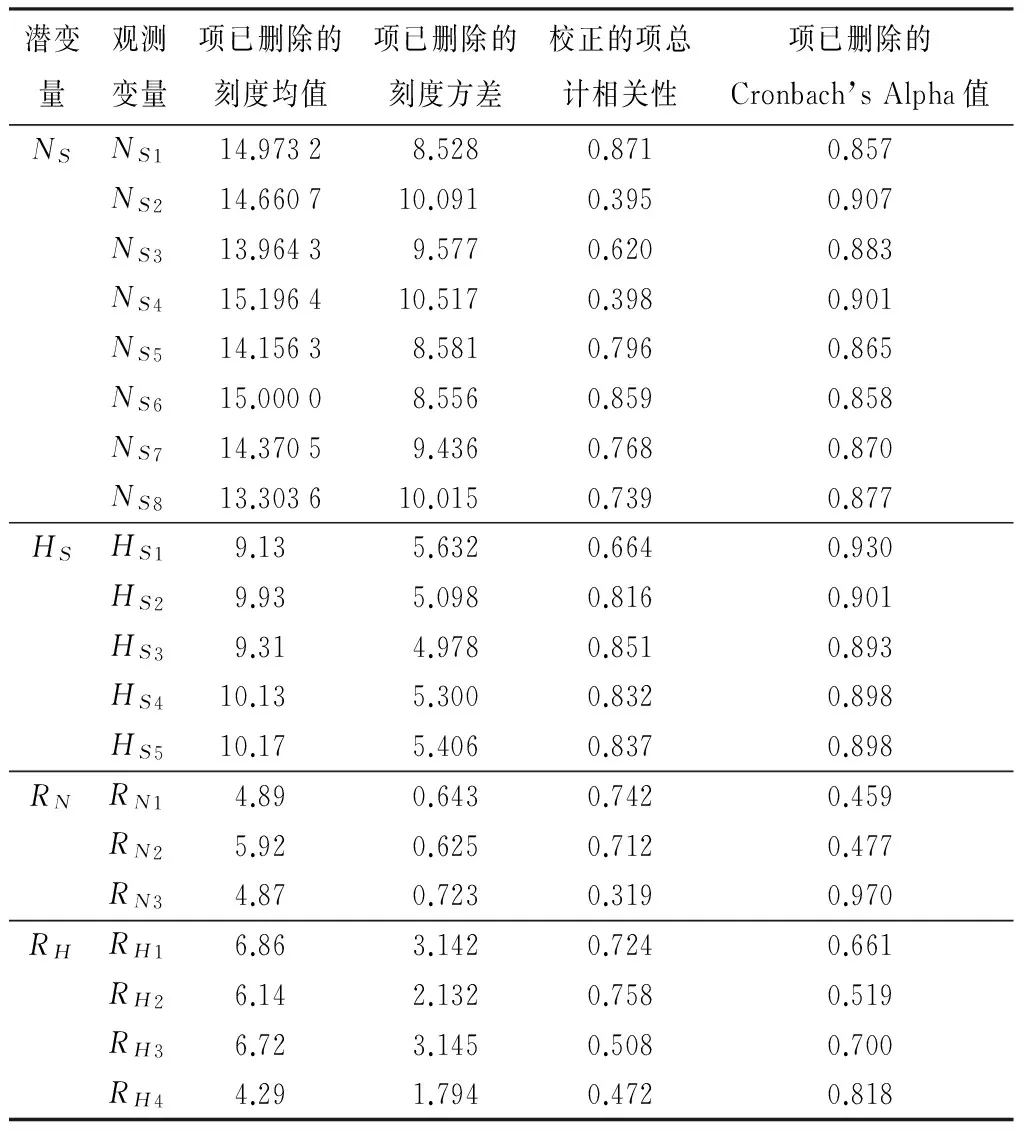
表1 项总计统计量

注：NS为湿地自我免疫及抗扰动能力；NS1为栖息地，NS2为生物量，NS3为水质，NS4为河道情况，NS5为净化能力，NS6为多样性，NS7为洪水调蓄能力，NS8为侵蚀控制能力。HS为湿地满足人类社会需求能力；HS1为人口健康状况，HS2为物质产品生产能力，HS3为居民预期健康寿命，HS4为休闲娱乐，HS5为物质生活指数。RN为自然扰动；RN1为气候适宜条件，RN2为外来物种，RN3为土壤肥力。RH为人类扰动；RH1为工业扰动强度，RH2为城镇化扰动强度，RH3为农业扰动强度，RH4为人类扰动强度。

表2 KMO的取值范围解释

2.3 验证性因子

验证性因子的分析方法与探索性因子分析不同，其主要是基于假设因子模型的拟合能力进行统计分析计算，通过已知因子对统计数据进行统计分析，对于观测变量因子的数量以及因子载荷两者之间的预期一致性进行检测分析[11]。在结构方程模型分析时，一般都是两种分析方法结合使用。本文分析中，主要基于探索性因子分析的统计结果，引入Lisrel8.7软件，进行验证性因子分析检测。由图3见：基于Standardized Solution方法的因子载荷，所有观测变量的S值都在0.5之上。

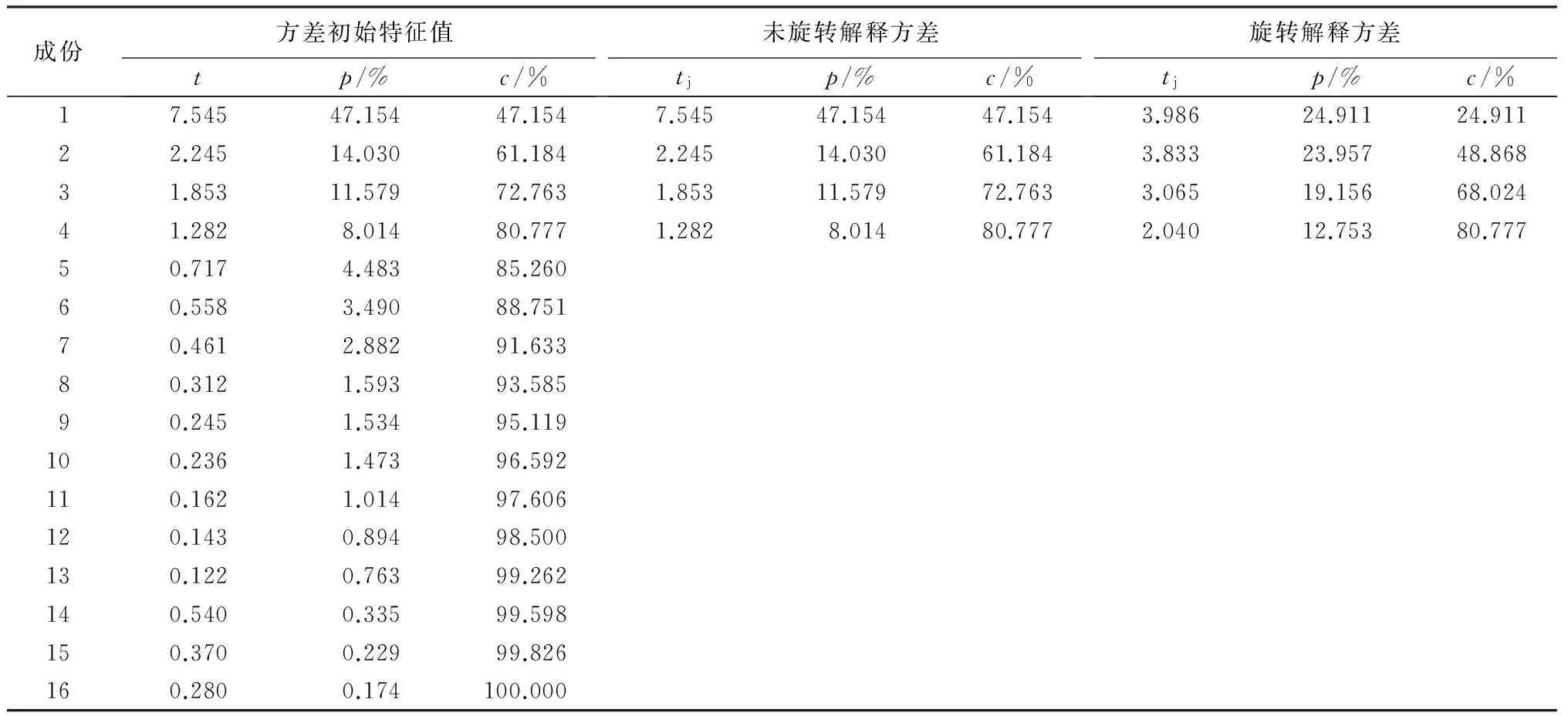
表3 总方差解释

注：提取方法为主成分分析。t为方差特征值合计；p为解释方差占总方差的比例；c为因子方差占总方差比例的累积；tj为解释方差特征值合计。

表4 旋转矩阵

注：旋转方法为具有Kaiser标准化的正交旋转法，旋转在5次迭代后收敛。RN1为气候适宜条件，RN2为外来物种；RH1为工业扰动强度，RH2为城镇化扰动强度，RH3为农业扰动强度；NS1为栖息地，NS3为水质，NS5为净化能力，NS6为多样性，NS7为洪水调蓄能力，NS8为侵蚀控制能力；HS1为人口健康状况，HS2为物质产品生产能力，HS3为居民预期健康寿命，HS4为休闲娱乐，HS5为物质生活指数。

2.4 结构方程模型修正及假设检验

通过验证性因子分析后，依据前文对模型的设计以及假设，结合扰动三江平原湿地生态系统健康关系的模型，进行结构方程模拟。

2.4.1 模型检验及修正

进行模型修正时，主要采用路径分析方法。可以分解为三个步骤：①根据理论假设，做出分析路径图；②通过路径图，列出相关系数与路径系数方程；③对列出方程求解。根据假设的模型结构进行路径分析，路径系数见图4，其对应的T值见图5。由图5可以看出，如果T值的绝对值小于1.96，则认为置信度α<0.05；只有当T的绝对值大于1.96，才认为置信度α>0.05，可以接受；RN—HS、RH—HS的T值绝对值都小于T值临界标准值1.96，因此需要将这两条关系路径删除。经过删除后的模型见图6。

图3 测量模型的路径系数

图7中，NS—HS1，湿地自我免疫与抗扰动能力与人的健康之间的直接显著关系并不明显，而且在修正模型后，由于修正的路径不多，不考虑添加路径。通过T值检验和MI值检验，修正了初始的结构方程模型，符合基本的拟合标准，得出修正后的结构方程模型路径图(见图8)。

图4 湿地生态系统健康与扰动因素结构方程模型路径系数

图5 湿地生态系统健康与扰动因素结构方程模型T值

2.4.2 模型的再检验

修正的湿地生态系统健康与扰动因素结构方程模型，符合基本的拟合标准后，还应对其进行整体拟合度评价。一般包括三大类指标：绝对拟合指数、增殖指数、简约拟合指数。由表5可见：模型有较佳的拟合程度，各个观测指标能够较好的解释对应的潜变量。

2.4.3 研究假设验证

通过以上数理统计分析，得出的计算结果说明选定的模型整体拟合程度较高，方法科学合理。可以认为：本文的各项假设条件，能够在各潜在变量的回归系数关系得到验证。观测变量的S值基本都在0.5的显著相关水平上，在本研究所列的5个假设中，其中的3个得到了验证。H1假设成立，说明自然扰动的健康度与三江平原湿地的抗扰动能力之间，具有直接的正相关性(β=0.24，T=3.05)；H2假设成立，说明人类扰动的健康度与三江平原湿地的抗扰动能力之间，具有直接的正相关性(β=0.65，T=7.67)；H3假设不成立，说明自然扰动的健康度与三江平原湿地满足人类社会需求的能力之间，具有不显著的关系(β=-0.03，T=-0.29)；H4假设不成立，说明人类扰动的健康度与三江平原湿地满足人类社会需求的能力之间，具有不显著的关系(β=-0.10，T=-0.78)；H5假设成立，说明湿地的抗扰动能力与满足人类社会需求的能力之间，具有直接的正相关性(β=0.65，T=6.26)。

图6 湿地生态系统健康与扰动因素结构方程模型T值删除路径图

图7 湿地生态系统健康与扰动因素因素结构方程模型MI值

表5 结构方程模型拟合指数

注：标准值来源于文献[12]。

2.5 模型结果

这些假设仅仅验证了4个潜变量之间的直接作用，并没有清晰的揭示潜变量之间的间接作用。在本文所涉及的4个潜变量中，为了全面分析其影响作用的大小、方向、机制等方面，在研究中把各潜变量之间的直接与间接效应和总效应关系进行分析(见表7)。

表7 潜变量之间的直接效应、间接效应和总效应

湿地生态系统健康的根本目的，在于人类健康及区域经济社会的可持续发展。因此，“湿地满足人类社会需求的能力”，是湿地生态系统健康的直接表现；“湿地满足人类社会需求的能力”，又受其他3个潜变量的影响。可以推出：直接健康指数=三江平原湿地满足人类需求的能力。在扰动与三江平原湿地生态系统健康的结构方程模型分析中，由于类需求的能力=0.15×自然扰动+0.42×人类扰动+0.65×湿地抗扰动能力，即间接健康指数。三江平原湿地生态系统健康指数，是由直接健康指数和间接健康指数共同决定的。

图8 修正的湿地生态系统健康与扰动因素结构方程模型路径系数

3 结束语

通过三江平原湿地生态系统健康与扰动因素结构方程模型的分析，可以看出：自然扰动和人类扰动，直接影响湿地自我免疫与抗扰动能力的发挥；同时，湿地自我免疫与抗扰动能力，又影响湿地满足人类社会需求能力，具有中介变量的属性。湿地生态系统健康的根本目的，在于人类健康及区域经济社会的可持续发展；湿地满足人类社会需求的能力，是湿地生态系统健康的直接表现，是直接健康指数。湿地满足人类社会需求的能力，间接受到自然扰动和人类扰动的影响；湿地自我免疫与抗扰动能力，是实现湿地满足人类社会需求能力的基础；他们共同影响湿地满足人类社会需求能力的发挥，是湿地生态系统健康的间接反映，也是间接健康指数。三江平原湿地生态系统健康指数，是直接健康指数和间接健康指数之和。实现三江平原湿地生态系统健康，要以提高湿地满足人类社会需求能力为根本目的，不单纯追求生态技术指标的数字化完美，也非以区域经济指标为唯一衡量标准；它是技术标准与社会认知的统一，是自然与人类社会健康发展的综合体现。

[1] 崔保山，杨志峰.湿地学[M].北京：北京师范大学出版社，2006.

[2] 李文艳，陈庆锋，李平.湿地评价方法研究综述[J].安徽农业科学，2010，38(15)：8135-8137.

[3] 崔丽娟，张明祥.湿地评价研究概述[J].世界林业研究，2002，15(6)：46-53.

[4] 戴建兵，俞益武，曹群.湿地保护与管理研究综述[J].浙江林学院学报，2006，23(3)：328-333.

[5] 崔保山，刘兴土.三江平原湿地生态特征变化及其可持续性管理对策[J].地域研究与开发，1999，18(3)：45-48.

[6] 姜秋香.三江平原水土资源承载力评价及其可持续利用动态仿真研究[D].哈尔滨：东北农业大学，2011：18.

[7] 鞠美庭，王艳霞.湿地生态系统的保护与评估[M].北京：化学工业出版社，2009：120.

[8] 李学娟，陈希镇.结构方程模型下的因子分析[J].科学技术与工程，2010，10(23)：5708-5711，5727.

[9] 钱璐璐.基于结构方程模型的宜居城市满意度影响因素实证研究[D].重庆：重庆大学，2010.

[10] 朱洪文，王淑杰，郑桂荣.统计学原理[M].哈尔滨：哈尔滨工业大学出版社，2000.

[11] 侯杰泰，温忠麟，成子娟.结构方程模型及其应用[M].北京：教育科学出版社，2004.

[12] 邱皓政，林碧芳.方程模型的原理与应用[M].北京：中国轻工业出版社，2009.