超高压输电线工频电场的分析

孙丽萍,杜丽娟,周宏威,何 杰

(东北林业大学,哈尔滨 150040)

超高压输电线工频电场的分析

孙丽萍,杜丽娟,周宏威,何 杰

(东北林业大学,哈尔滨 150040)

针对超高压输电线路对电磁环境影响很大的问题,阐述了比例边界有限元方法计算工频电场的方法,基于麦克斯韦方程组,建立了相应的电场计算模型,利用变分原理通过比例边界坐标变换,推出工频电场的比例边界有限元方程,分析了高压输电线路在空旷地点与穿越树木时的工频电场。计算和仿真结果表明:比例边界有限元法能够准确计算出工频电场,减少了数据准备工作量;树木对电场有明显的削弱作用。

高压输电线路; 工频电场; 建模; 比例边界有限元方法

目前,220 kV的高压乃至500 kV的超高压输电线路已经不断的接近人们的生活区域,输电线路对电磁环境的影响很大,准确快速地计算出电场及降低电场对环境的影响就成为急需解决的问题。计算工频电场的研究方法很多,主要有模拟电荷法、有限元法、边界元法等[1-10],但都有一定的缺陷:用模拟电荷法时电荷个数和位置很难确定;有限元法是全域算法,需要把所有的求解域离散,计算量较大;边界元法是对求解域边界上划分单元,降低了求解问题的维数,基本解的寻找很困难;Wolf和Song在20世纪90年代提出的比例边界有限元法,结合了有限元法和边界元法的优势,仅需要用有限元离散部分边界就可以把问题降低一维,在无离散的坐标方向利用解析方法求解,在工频电场方向的应用很少见。而在实际计算电场时,经常遇到在某边界上给定电位的情况,由此,本文基于比例边界有限元建立模型,从静电场控制方程——Laplace’s方程开始,结合变分原理推导了比例边界有限元法,并成功用于计算工频电场,同时,将树木对电场是否有影响进行了仿真研究,以期为输电线路架设提供一定参考。

1 架空输电线路的选取与模型建立

架空输电线路主要由杆塔(电杆和铁塔)、导线、避雷线、绝缘子和金具等组成。拉线塔可以分为拉线、塔头和主柱3个部分。塔头和主柱一般由角钢组成,角钢采用空间架结构,该结构有很好的整体稳定性,可以承受较大的拉力,由于拉线塔充分利用了材料的强度特性,故达到了减少材料损耗用量的目的。拉线塔从外形来分有多种形式:一种是导线呈三角形排列的,例如:鸟骨型、猫头鹰型等;另一种是导线呈水平排列的,例如门型、V型;还有一种纵向能自立的,例如内拉线门型塔等。

以林场里的单回三相三角形输电线路为原型建立模型,如图1所示。

图1 500 kV单回三相水平排列线路

对长距离的输电线路的电场分析做以下理想假设:大地看作是电位为零的无穷大导体面;无限长直导线看作与地面平行的光滑圆柱体,并且其表面也视为等位面;忽略杆塔、导线临近物体以及避雷线的端部效应和弧垂影响[11]。简化后,长距离高压输电线路中的电场问题可转化为多个平行导体系统的二维交变电场计算问题,即二维静电场问题。三相导线等效半径计算的表达式为

(1)

式中:R为分裂导线半径;n为次导线根数;r次导线半径;i为不同相的顺序U、V、W相。

三相输电线各相导线电压可表示为

(2)

式中θ为初相。

2 比例边界有限元方程应用于电场的公式推导

描述静电场的控制方程为拉普拉斯方程，即

2φ=0

(3)

式中:φ为电位;为梯度算子。

(4)

(5)

式中:n为边界外法线方向,对于研究的区域有两类边界条件,一类是S1是给定电位值,也称第一类边界;S2称第二类边界[12]。

式(3)—式(5)的等效泛函问题可以表达为

(6)

在比例边界有限元方法中,包含有径向(ξ)和圆周方向(s)的坐标系统如图2所示,径向坐标规定在比例中心(Scaling Center)处定义为零,而在边界上定义为单位值1;圆周方向坐标规定沿着边界逆时针方向的距离。如果0≤ξ≤1 表示有限区域问题,如果ξ→∞表示开域问题。

比例边界坐标系统和Cartesian坐标系统的关系为

x=x0+ξx(s)

y=y0+ξy(s)

(7)

利用式(7),计算域内任意一点的位置可由比例坐标系中的坐标分量ξ和s确定。

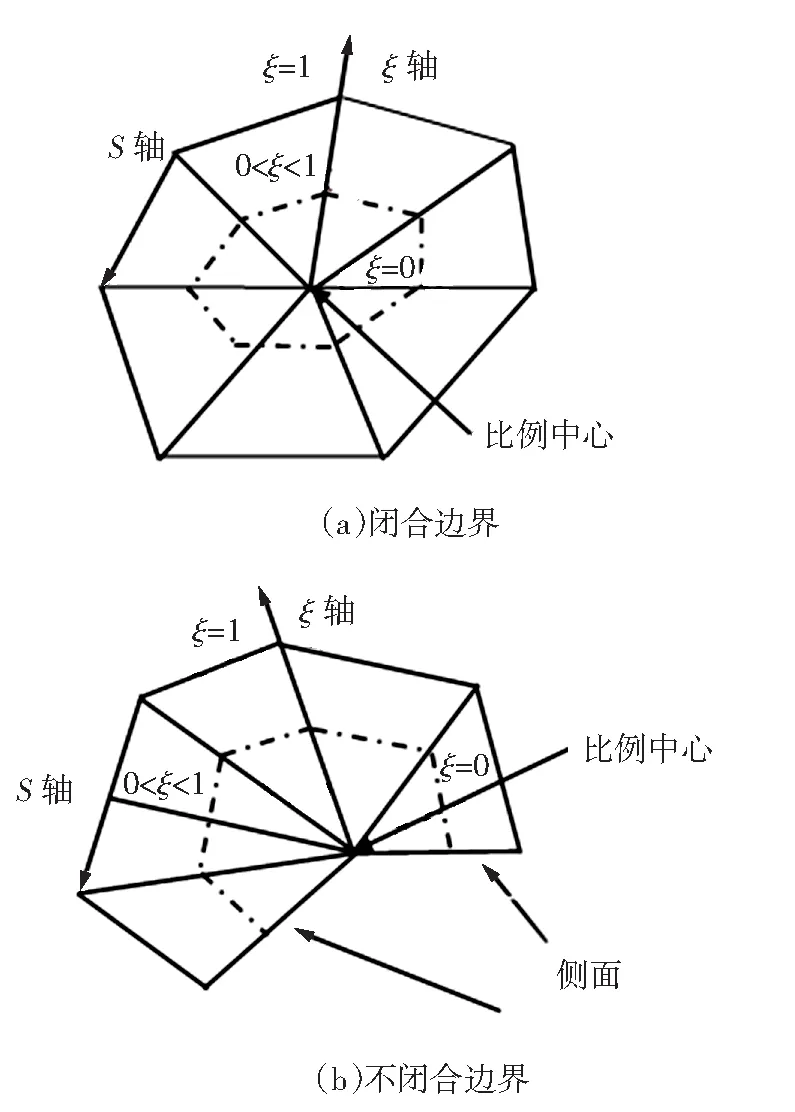
图2 比例边界坐标系统

Cartesian坐标系下的梯度算子在比例坐标系下可变换为

(8)

其中

(9)

雅克比行列式定义为

|J|=x(s)y(s)s-y(s)x(s)s

(10)

通过雅克比矩阵,可得比例边界有限元坐标和Cartesian坐标两者之间的转换关系:

(11)

根据等参变换概念,电位也可以采用插值函数N(s)进行离散:

φ(ξ,s)=N(s)φ(ξ)

(12)

将式(8)和式(12)带入式(6)可得:

(13)

其中:

B1(s)=b1(s)N(s)

(14)

B2(s)=b2(s)N(s)s

(15)

引入系数矩阵,则有

(16)

(17)

(18)

(19)

考虑δφ(ξ)T的任意性,可产生如下关系式:

-E2φ(ξ)+ξFs(ξ)=0

(22)

式(20)、式(21)分别是计算域内、外边界条件方程。式(22)是比例边界有限元的基本方程。

3 比例边界有限元方程求解

当Fs(ξ)=0时,式(22)为二阶Euler-Cauchy齐次方程。为了求解方便,降阶求解,引入Q(ξ)作为φ(ξ)的对偶变量:

(23)

可得状态方程:

(24)

其中:

(25)

由于Z阵为Hamilton阵,可以通过求解Z的特征值问题来得到方程(24)的解:

(26)

式中:λi为特征值对角矩阵;Φ11、Φ12、Φ21、Φ22均为特征向量矩阵。

进一步可得:

φ(ξ)=Φ11ξ-λic1+Φ12ξλic2

(27)

Q(ξ)=Φ21ξ-λic1+Φ22ξλic2

(28)

式中:c1、c2为积分常数;ξ-λi、ξλi为对角矩阵。

对于有限域的问题,ξ=0处的φ为有限值,所以c2=0;对于无限域的问题,ξ=∞处的φ为有限值,所以c1=0。其中,有限域的积分常数c1和无限域的积分常数c2都可以由边界条件来确定。c1、c2确定后,可以通过插值确定域内任意点的电位和E=-φ确定域内任意点电场强度。计算输电线的场下电场强度可分别按式(2)的实部和虚部导线设置的边界条件计算两次电场强度。最后就可以得到的总和成电场强度为

(29)

式中:ExR、EyR分别为导线电压为实部时计算的x、y向的电场强度;Ex1、Ey1分别为导线电压为虚部时计算的x、y向的电场强度。

当Fs(ξ)≠0时,式(22)为非齐次方程。同样引入Q(ξ),即式(23),可得状态方程:

(30)

由此可以得出φ(ξ)和Q(ξ)的表达式:

φ(ξ)=Φ11ξ-λic1(ξ)+Φ12ξλic2(ξ)

(31)

Q(ξ)=Φ21ξ-λic1(ξ)+Φ22ξλic2(ξ)

(32)

式中:c1、c2是积分常数,可以通过边界条件获得；c1(ξ)和c2(ξ)为变异系数,由式(30)可以得出:

(33)

(34)

其中:

(35)

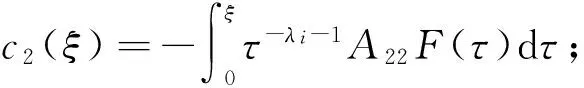
4 输电线下有无树木时电场的分析

单回三相三角形的输电线路如图1所示,采用4×LGJ—400/50导线,线间距离为2×7.5 m,H1=15 m,H2=11 m,电阻率为2.8264E-8,r=0.0148,R=0.457,由式(1)算出等效导线半径是0.274 m。现设初相为45°,三相各个导线电压可由式(2)计算出。输电线路划分为有限域和无限域,两种情况的比例边界有限元计算示意图如图3所示。计算模型均包括9个有限域与1个无限域。

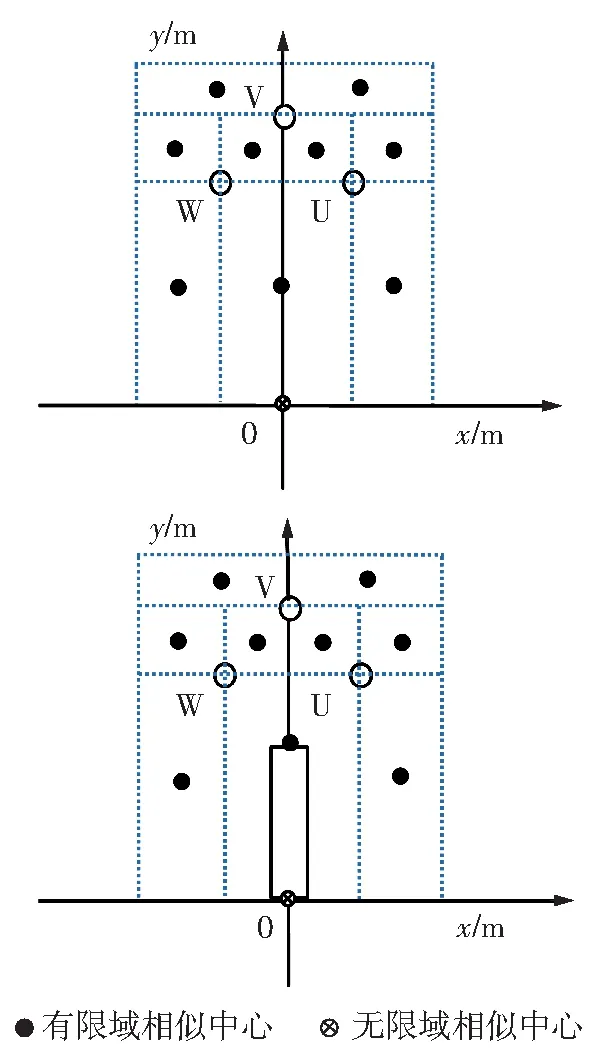
图3 有无树木的比例边界有限元计算示意图

Fig.3 Schematic diagram of scaled boundary finite element calculation with tree and without tree

在Ansys14.5中,利用APDL语言快速建立模型,并进行网格划分,网格划分结果如图4所示。根据比例边界有限元的原理只选取10个区域上的边界节点(选取节点采用的命令流是NSEL、TYPE、 ITEM,、COMP,、WMIN、 VMAX,、VINC、KABS),对选取的节点进行计算,采用输电线路电场监测的标准方法,取距地1.5 m处测量电场强度。

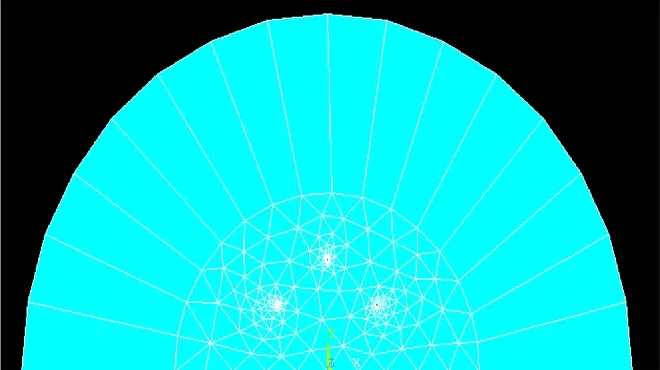
图4 网格划分

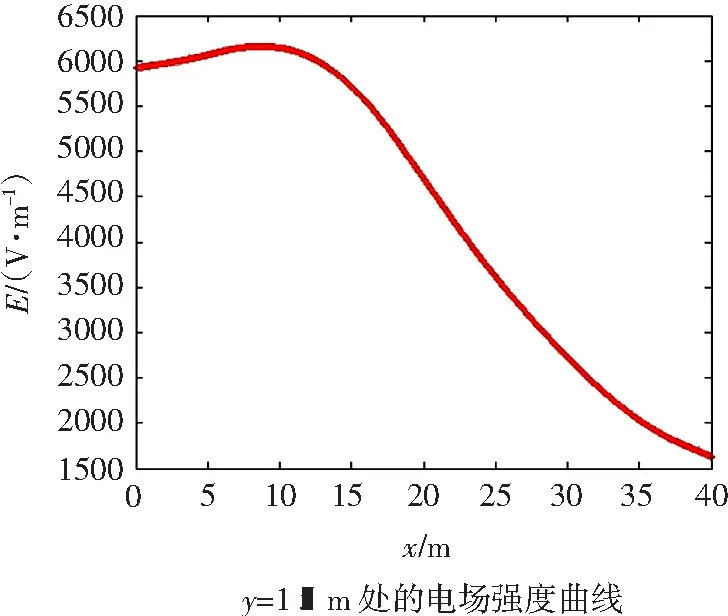
图5 输电线下无树木时电场情况

对空旷地点的超高压输输电线路的电场用SBFEM模拟,如图5所示,得知场强的分布与距离地面1.5 m处的电场强度曲线,该结果与大部分文献的计算结果相同,说明该方法可以应用于计算电场,最大值在距线路中心10 m处。对有树地点的超高压输电线路的电场用SBFEM模拟,如图6所示。

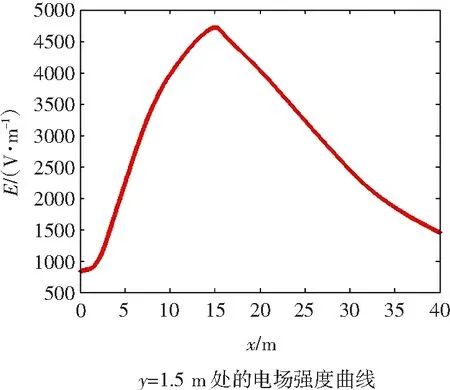
图6 输电线下无树木时电场情况

Fig.6 Electric field under transmission line when no trees

对比图5和图6,从距离地面1.5 m处的电场强度曲线看,可知电场强度曲线的走向是一致的。有树木时,电场强度有很大的削弱。对于以上现象进行分析,发现距地面1.5 m处电场强度变弱是因为树的树干和树叶对电场能量进行吸收,削弱了电场强度。因此,扩大种植树木的范围可以更好地减小电场强度。扩大树木的范围后进行仿真所得的结果如图7所示,与图6结果对比,可以看出电场强度大约减少了1500 V·m,由此得知扩大树木的范围能削弱电场强度。

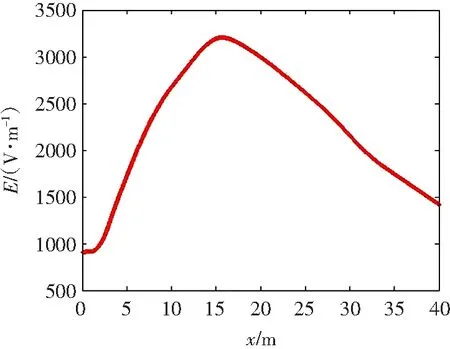
图7 扩大树的范围时y=1.5 m处的电场强度曲线

Fig.7 Electric field intensity curve ofy=1.5 m when expanding trees range

5 结 论

1) 利用比例边界有限元法对输电导线下方的工频电场进行计算,可以成功应用于电场方向并减少了计算量。

2) 利用比例边界有限元法对空旷地点和有树时输电导线下方的工频电场分别计算,发现树木对工频电场具有很强的削弱作用。通过仿真对比,可知树木范围越大,对电场强度的削弱越强。建议在输电线走廊附近多植树,设立起自然保护屏障区,有效防止电磁对环境的污染。

[1] 谢辉春,张建功,张小武,等.基于模拟电荷法对 500 kV 输电线路跨越民房时导线高度的计算[J].电网技术,2008,32(2):34-37. XIE Huichun, ZHANG Jiangong, ZHANG Xiaowu, et al. Charge simulation method based calculation and research on conductor heights of 500 kV transmission lines passing over residences [J]. Power System Technology, 2008,32(2):34-37.

[2] 杨勇,陆家榆.基于Deutsch假设法和有限元法的高压直流线路地面合成电场对比分析[J].电网技术. 2013,37(2):526-532. YANG Yong, LU Jiayu. Contrast and analysis on total electric field at ground level under HVDC transmission lines by Deutsch assumption-based method and finite element method [J]. Power System Technology, 2013,37(2):526-532.

[3] 刘士利,王泽忠,孙静. 基于线-面模型的边界元法计算特高压交流变电站设备附近工频电场[J].电工技术学报. 2011,26(3):162-167. LIU Shili, WANG Zezhong, SUN Jing. Calculation of power frequency electric field near equipments in UHV substations with BEM based on line-area models [J]. Transactions of China Electrotechnical Society, 2011,26(3):162-167.

[4] 黄子璇,席黎明,樊梦旭,等.高压输电线下有建筑物时工频电场计算中模拟电荷设置方法的改进[J].电网技术. 2013,37(3):788-793. HUANG Zixuan, XI Liming, FAN Mengxu, et al. Improvement of simulation charge setting in calculation of power frequency electric field of high voltage transmission line above buildings [J]. Power System Technology, 2013,37(3):788-793.

[5] ADEL Z E D,MOHAMED A A W,The effects of the span configurations and conductor sag on the electric-field distribution under overhead transmission lines[J].IEEE Transactions on Power Delivery,2010,25(4):2891-2902.

[6] 黄道春,阮江军,文武,等.特高压交流输电线路电磁环境研究[J].电网技术,2007,31(1):6-11. HUANG Daochun, RUAN Jiangjun, WEN Wu, et al. Study on electromagnetic environment of UHV AC transmission lines [J]. Power System Technology, 2007,31(1):6-11.

[7] 吴桂芳,陆家榆,邵方殷.特高压等级输电的电磁环境研究[J].中国电力,2005,38(6):24-27. WU Guifang, LU Jiayu, SHAO Fangyin. Research on electromagnetic environment of the next voltage level of transmission system in China [J]. Electric Power, 2005,38(6):24-27.

[8] 邬雄.1000 kV 交流输电线路电磁环境的研究[J].电力设备,2005,6(12):24-27. WU Xiong. Study on electromagnetic environment for 1000 kV ac transmission line [J]. Electrical Equipment, 2005,6(12):24-27.

[9] 俞集辉,周超.复杂地势下超高压输电线路的工频电场[J].高电压技术,2006,32(1):18-24. YU Jihui, ZHOU Chao. Power frequency electric field of EHV transmission lines under condition of complex landscape [J]. High Voltage Engineering, 2006,32(1):18-24.

[10] 陈楠,文习山,刘波,等.高压输电导线三维工频电磁场计算与测量[J].电网技术,2011,35(3):159-164. CHEN Nan, WEN Xishan, LIU Bo, et al. Calculation and measurement of three-dimensional power frequency electrical and magnetic field under transmission line [J]. Power System Technology, 2011,35(3):159-164.

[11] 苏国政,黄道春,余世峰,等.特高压紧凑型输电线路工频电场强度计算[J].武汉大学学报. 2007,40(3):99-102. SU Guozheng, HUANG Daochun, YU Shifeng, et al. Calculation of power frequency electric field intensity of ultrahigh voltage compact transmission lines [J]. Engineering Journal of Wuhan University, 2007,40(3):99-102.

[12] 徐禄文.输电线路跨越建筑物电场计算探讨[J].电力建设,2011,32(9):42-46. XU Luwen. Discussion on electric field calculation for power lines over building [J]. Electric Power Construction, 2011,32(9):42-46.

(责任编辑 侯世春)

Analysis of power frequency electric field of EHV transmission lines

SUN Liping, DU Lijuan, ZHOU Hongwei, HE Jie

(Northeast Forestry University, Harbin 150040, China)

Aiming at the strong influence of EHV transmission line on electromagnetic environment, this paper expounds how to calculate power frequency electric field by scaled boundary finite element method, establishes the calculation model for the relevant electric field based on Maxwell’s equations, deduces the scaled boundary finite element equation of power frequency electric field through variational principle based scaled boundary coordinate conversion, and analyzes the power frequency electric field of EHV transmission lines when there are trees and no trees. The result of calculation and simulation shows that scaled boundary finite element method is able to accurately calculate power frequency electric field and to lessen data preparation; trees weaken electric field.

EHV transmission lines; power frequency electric field; modeling; scaled boundary finite element method

2015-02-06。

孙丽萍(1958—),女,教授,研究方向为电磁场和复杂系统建模与控制。

TM751

A

2095-6843(2015)04-0286-05