LFM脉冲压缩雷达的移频干扰技术研究
2015-03-10顾成虎曲丽娜
顾成虎,曲丽娜
(哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001)
LFM脉冲压缩雷达的移频干扰技术研究
顾成虎,曲丽娜
(哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001)
脉冲压缩雷达能够同时提高雷达的作用距离和距离分辨率,在现代雷达中被广泛采用.由于线性调频脉冲压缩雷达的距离-多普勒频移之间存在强耦合现象,使其比常规雷达更易受移频干扰.对单假目标移频干扰、线性函数移频干扰和分段线性函数移频干扰进行了理论分析和Matlab仿真验证,并对各种干扰进行比较和分析.仿真实验证明了理论分析的正确性和有效性,在工程实践上提供了对抗脉冲压缩雷达的理论指导.
脉冲压缩雷达;单假目标移频干扰;线性函数移频干扰;分段线性函数移频干扰
线性调频脉冲压缩雷达较好地解决了雷达作用距离与距离分辨力之间的矛盾,在现代雷达体制中得到广泛应用[1].与此同时,针对线性调频脉冲压缩雷达的干扰研究一直以来也是雷达电子战领域的研究热点.因线性调频脉冲压缩雷达的距离-多普勒频移之间存在强耦合现象,使其比常规雷达更易受转发式干扰机干扰,干扰机通过对截获的雷达发射信号调制一个附加的频率后再转发给雷达,对敌方雷达起到干扰的目的[2].
移频干扰是对抗脉冲压缩雷达的主要方式,文献[3-4]提出了单假目标移频干扰算法,通过移频可以产生超前和延后的单假目标,形成欺骗干扰的目的.文献[5-7]提出了线性函数移频干扰算法,通过线性函数移频,能形成覆盖干扰效果.文献[8]用锯齿波加权调频方式来对线性调频雷达进行干扰,实现了覆盖干扰效果.文献[9]通过对移频干扰性能参数的推导,得出当频偏比较小时,以欺骗干扰为主;当频偏比较大时,移频干扰产生的波形严重失真,以压制干扰为主.
上述文献进行了部分理论分析和仿真验证,但没有对线性函数移频干扰就具体干扰实例进行具体的分析和论证.在以上文献的研究成果基础上,本文对单假目标移频干扰和线性函数移频干扰进行了进一步理论分析研究,对分段线性函数移频干扰进行了详细的理论分析,并针对各干扰方式进行了具体目标检测实例的仿真实验.
1 移频干扰原理
1.1 单假目标移频干扰原理
干扰信号是对截获的线性调频雷达信号进行调制后转发而形成的,干扰信号进入雷达接收机后,相对于线性调频信号S(t),其信号频率发生了ξ的频移,移频干扰信号为:
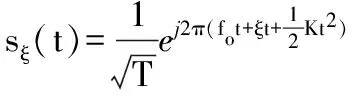
(1)
其中:ξ为调制的移频量,干扰信号经过匹配滤波器进行脉冲压缩处理后,得到输出信号为:
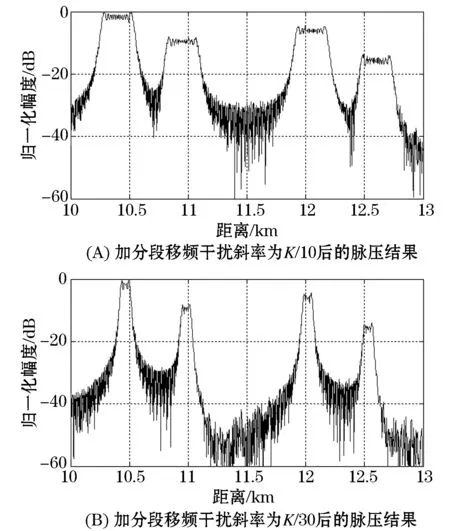
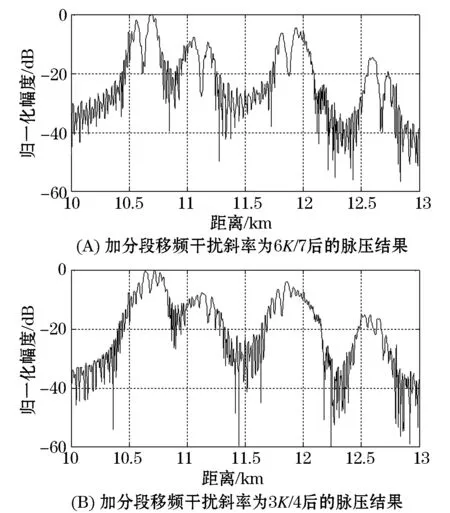
(2)
上式中t取值范围为|t| |yξ(t)|= (3) 当移频量为零时,即为无干扰的情况.而当移频量ξ≠0时,尖峰将偏移到T-ξ/K处,当ξ>0则形成的干扰主峰超前,当ξ<0时干扰主峰将会延后[3],形成超前或延后距离为ΔS=c·ξ/2K的假目标. 1.2 线性函数移频干扰原理 调频斜率是脉冲压缩雷达信号的一个重要特征参数,它表征了线性调频信号频率的变化趋势和变化剧烈程度.线性函数移频干扰就是干扰频率按线性函数变化.假设在整个脉冲宽度内,干扰机调制的初始频率为ξ0,调频斜率为Kξ,则干扰本身的调制带宽为Bξ,形成覆盖干扰,干扰信号表示如下[3]: (4) 其频谱为: (5) 干扰信号经过匹配滤波器后输出信号频谱为: (6) 再经过傅里叶反变换得到输出信号的时域表示为: (7) 经过整理近似计算后得到干扰峰值为: (8) 覆盖干扰的距离宽度为: (9) 1.3 分段线性函数移频干扰原理 分段线性移频就是把整个脉冲宽度T均匀分为N段.参数有多种取值方式,可以调整起始调制频率ξn,只要起始调制频率在原线性调频信号附近即可.分段数的选取要根据具体信号的脉宽进行分段,并且每一段的线性移频斜率可以有多种取值方式.本文为了分析问题的简便,这里取各段线性移频斜率Kξ都相等,移频规律如图1所示. 图1 分段线性函数干扰信号瞬时频率 干扰信号为接收到的雷达信号与一锯齿波调频信号p(t)的乘积,干扰信号表示如下[9]: (10) 锯齿波信号p(t)是一个周期信号,单个周期的表示式为: exp(j2πusawt2/2)(n-1)ΔT≤t≤nΔT (11) 则 p(t)=pn(t)*∑δ(t-nΔT) (12) 很容易知道pn(t)也是一个线性调频信号,其调频斜率为usam=K*Kζ,带宽表示为Bsaw=usawΔT,定义Dsaw=Bsaw*ΔT为pn(t)的时宽带宽积,当Dsaw≫1时 的频谱接近于矩形,表示为Pn(f).容易得到p(t)的频谱为: P(f)=∑fsawPn(f)δ(f-nfsaw) (13) 对每一段线性移频干扰信号,都是一个窄的失配的线性调频脉冲,故每段干扰信号频谱都是一个小矩形信号.周期信号p(t)的频谱包络为等幅梳齿状,谱包络的宽度为Bsaw,每个小梳齿的间隔为fsaw. 分段线性函数移频干扰信号的幅度谱如图2所示,选取T=120 μs,N=6,6段信号的起始频率分别为-6MHz、-4MHz、-2MHz、0MHz、2MHz、4MHz,线性移频斜率为Kξ=K/2=0.05MHz/μs,由图2可知分段线性函数干扰信号的幅度谱由6段小的频谱组成,仿真结果与理论分析一致. 图2 分段线性函数干扰信号幅度谱 分段线性移频干扰就是更加细化了的线性函数移频干扰,由上面分析知道线性函数移频干扰信号与接收信号产生失配现象,会产生被展宽的多个假目标,实现覆盖干扰和欺骗干扰的双重效果. 为了验证上文提到的几种干扰对线性调频脉压雷达的干扰效果,本文用Matlab进行仿真验证.本实验选用的技术指标如下: 中心频率f0:0 MHz;带宽B:50 MHz;采样率fs:80 MHz;脉冲宽度T:40 μs. 四个目标距离分别为:10.5、11、12、12.5 km,未加移频干扰信号的脉压输出仿真结果如图3所示. 图3 未加移频干扰的脉压输出结果 实验1:单假目标移频干扰 加单假目标移频干扰,调制的干扰移频量ξ=±1MHz.当移频量ξ≠0时,就会形成超前或延后距离ΔS=c·ξ/2K的假目标,仿真结果如图4(A)和图4(B)所示.当调制的干扰移频量分别为、时形成超前和延后目标距离为的假目标,仿真结果与理论分析一致. 图4 经单假目标移频干扰后敌方会收到超前或者延后的单个假目标,即假目标和真目标会同时暴露在敌方视野之中,干扰假目标个数较少时很多时候不能起到干扰敌方的目的.当多个目标同时存在时会发现超前或者延后相等距离差的假目标,敌方很容易通过这一特性察觉到干扰的存在.假目标很容易成为信标,以此来确定真目标的具体位置,单假目标移频干扰很可能会暴露真实目标. 实验2:线性函数移频干扰 加线性函数移频干扰,移频干扰斜率Kξ分别为K/10和K/30,仿真结果如图5(A) 和图5(B)所示.经线性函数移频干扰后目标信号被展宽的单个覆盖干扰所覆盖,并且图5(A)的展宽量明显大于图5(B),与式(9)的理论分析结果一致.同时由式(8)可知为使真目标完全覆盖在被展宽的假目标干扰信号中,干扰机还要提高干扰机的发射功率,这对干扰功率的设置有理论上的指导意义. 图5 仿真结果 实验3:分段线性函数移频干扰 加分段线性函数移频干扰,将脉冲压缩雷达的脉冲宽度均匀分成4段,仿真结果如图6 (A)和图6 (B)所示,线性移频干扰斜率Kξ分别为6*K/7和3*K/4,目标的脉压输出信号全部都被干扰假目标群所覆盖. 图6(B)脉冲压缩输出信号明显比图6(A)中的输出结果要宽,这与式(9)的分析结果吻合,由式(8)知随干扰斜率的升高,脉压输出信号幅度会降低,这就要求干扰机提高自己的发射功率才能起到比较好的干扰效果. 图6 仿真结果 本文研究结果表明:三种移频干扰将分别产生单个假目标距离欺骗干扰、单个覆盖干扰、多个逼真假目标群的欺骗和覆盖干扰.单假目标移频干扰过于简单且很多时候不能起到干扰敌方的目的,线性函数移频干扰产生了展宽的覆盖干扰,只要干扰参数设置合适就能起到较好的干扰效果.通过研究还发现分段线性函数移频干扰不仅能产生展宽的假目标信息,还会产生逼真假目标群,起到欺骗干扰和覆盖干扰的双重干扰效果.本文的研究结果将为干扰战术的实施提供理论指导,对工程的顺利进行提出一种新形势的实施方略. [1] 赵忠凯, 尹 达. 基于FPGA的数字正交变换信号的脉冲压缩[J]. 哈尔滨商业大学学报: 自然科学版, 2013, 29(6): 682-685. [2] HUANG X H, ZHOU Y Y, JING W,etal. A frequency-based inter/intra partly coherent jamming style to SAR[C]// Dalian: 2nd International Conference on. IEEE, 2010.434-437. [3] 刘建成, 刘 忠, 王雪松, 等. 基于群延迟的前移干扰研究[J]. 自然科学进展, 2007, 17(1): 99-105. [4] 罗金亮, 王松山, 孙 浩. DRFM移频干扰对LFM脉冲压缩雷达的影响及对策研究[J]. 舰船电子对抗, 2009, 32(3): 18-20. [5] 吕 波, 冯 起, 袁乃昌. 对LFM脉压雷达的移频压制干扰技术研究[J]. 现代雷达, 2009, 31(1): 9-12.[6]YANGY,ZHANGW,YANGJ.Studyonfrequency-shiftingjammingtolinearfrequencymodulationpulsecompressionradars[C]//Nanjing:WirelessCommunications&SignalProcessing,InternationalConferenceon.IEEE, 2009.1-5. [7] 潘小义, 王 伟, 熊跃军, 等. 相干移频干扰幅度补偿技术研究[J]. 现代防御技术, 2010(3): 90-93. [8] 张 煜, 杨绍全, 崔艳鹏. 对线性调频雷达的锯齿波加权调频干扰[J]. 西安电子科技大学学报, 2007, 34(2): 209-212. [9] 黄翀鹏, 王 剑, 徐保国. 线性调频脉冲的移频干扰性能研究[J]. 系统工程与电子技术, 2013, 35(5): 935-939. Study on frequency-shifting jamming to LFM pulse compression radar GU Cheng-hu, QU Li-na (School of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China) Pulse compression radar is widely used in modern radar for its improvement of detection range and range resolution. Its strong coupling phenomenon between detection range and the doppler shift, make it more vulnerable to interference than conventional radar. In this paper, the theoretical analysis and Matlab simulation of single false target frequency-shifting jamming, linear function frequency-shifting jamming and piecewise linear function frequency-shifting jamming were successively carried out. Simulation experiments showed the correctness and effectiveness of the theoretical analysis and provide theoretical guidance to resist pulse compression radar in engineering practice. pulse compression radar; single false target frequency-shifting jamming; linear function frequency-shifting jamming; piecewise linear function frequency-shifting jamming 2014-05-13. 中央高校基本科研费专项基金(HEUCF140803) 顾成虎(1989-),男,硕士,研究方向:宽带信号检测与识别,雷达信号侦察与干扰. TN972 A 1672-0946(2015)03-0350-04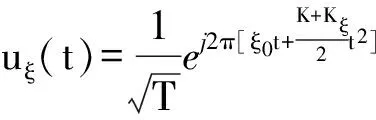



2 计算机仿真分析


3 结 语
