微机械陀螺正交耦合误差静电力抑制的有限元仿真研究
2015-03-10窦茂莲林梦娜郭中洋
窦茂莲,刘 飞,林梦娜,郭中洋
(北京自动化控制设备研究所,北京100074)
微机械陀螺正交耦合误差静电力抑制的有限元仿真研究
窦茂莲,刘 飞,林梦娜,郭中洋
(北京自动化控制设备研究所,北京100074)
微机械陀螺的正交耦合误差是敏感结构振动模态间的刚度耦合引起的检测模态输出偏量,是影响陀螺性能的关键误差源之一。静电力抑制是一种采用静电力调节驱动模态的主轴偏量,使用直流电压进行正交耦合误差抑制的方法,该方法具有片上实时抑制能力,能够有效抑制正交耦合误差。从静电力抑制正交耦合误差的基本原理出发,运用有限元仿真,对硅基音叉陀螺正交耦合误差的静电力抑制进行了仿真分析,并通过实物测试数据进行了验证。
微机械陀螺;正交耦合误差;静电力抑制;有限元仿真
0 引言
微机电陀螺是指采用微加工工艺制造,特征尺寸在微米量级,用于敏感载体相对于惯性空间角运动的仪表。微机电陀螺大都基于哥式振动效应,利用驱动和检测两个正交模态,实现对旋转向量的敏感[1]。
理想情况下,陀螺驱动和检测模态间的耦合仅通过科氏力传递。实际陀螺的两个工作模态间存在驱动力、阻尼、刚度等多种耦合,其中驱动模态到检测模态的刚度耦合是微机电陀螺的一个主要误差源,该耦合误差在相位上与角速度正交,因此称为正交耦合误差。正交耦合误差与角速度之间存在90°的相位角,这意味着可以通过相敏解调将这两个信号区别开来。但是,当正交耦合信号的幅值和相位随时间变化时,输出的偏移量也随之变化,从而直接影响陀螺的零偏稳定性。为提高陀螺性能,必须尽可能减小甚至消除正交耦合误差。
正交耦合误差抑制的方法主要有:机械隔离、机械修调、静电力矫正以及采用解耦梳齿等[2-5]。其中,静电力矫正具有片上实时调节能力,且抑制精度较高[5]。
本文主要围绕硅基平面振动式音叉陀螺正交耦合误差的静电力抑制开展有限元仿真研究,文章采用理论分析、有限元仿真与实物测试相结合的方式,对直流电压作用下的矫正电极对敏感结构正交耦合误差的抑制能力进行了分析,为陀螺矫正电极、电路的设计工作提供支撑。
1 静电力矫正原理
正交耦合误差主要来源于驱动到检测模态的刚度耦合。在适当的电极排布下,施加适当的直流电压能够产生与刚度耦合相抵消的静电力作用,从而实现对正交耦合误差的抑制。
1.1 微机电陀螺误差模型
图1所示为振动式陀螺的简化模型,图1中驱动模态振动沿x方向,检测模态振动沿y方向;m为科氏力敏感部分质量;kd、ks分别表示驱动和检测模态的广义刚度;cd、cs分别表示驱动和检测模态的阻尼系数;Ωz为外界角速度输入。
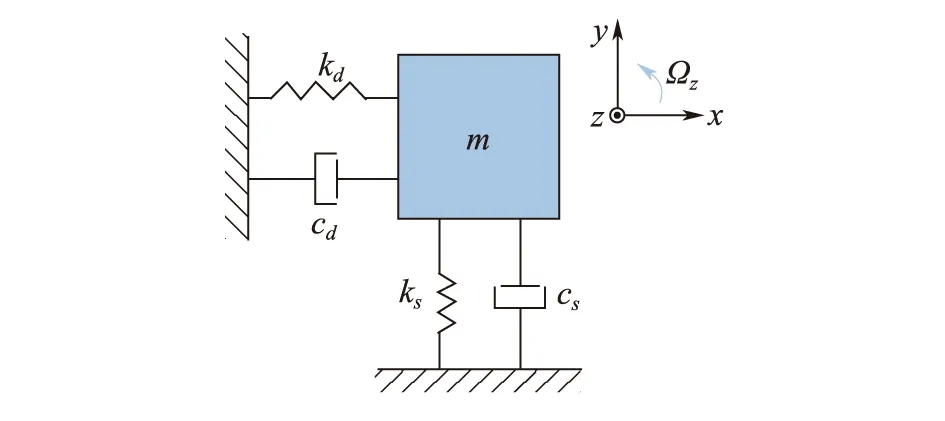
图1 振动陀螺基本模型Fig.1 Simplified model of in-plane vibrating gyroscopes
Weinberg和Kourepenis对硅基平面振动式音叉陀螺的耦合误差源进行了分析[6],考虑在力耦合、阻尼耦合和刚度耦合时,陀螺的动态微分方程可以表示为:
驱动
(1)
检测
(2)
其中,x、y分别表示驱动和检测模态的振动位移;md、ms分别表示驱动和检测模态的广义质量;Fd为驱动力;kds为模态间刚度耦合系数;cds为模态间阻尼耦合系数;α为驱动力耦合系数。
在刚度耦合误差源作用下,检测模态的动态响应为
(3)
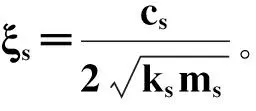
刚度耦合项作用下检测模态的动态输出即为正交耦合误差。
1.2 静电力矫正原理
图2所示为静电矫正电极的一种典型排布形式。图2中,Vp为质量块上的直流偏压;Vdc为静电矫正电极上的直流电压;L0为电极间重叠部分的长度;d0为电极间距。
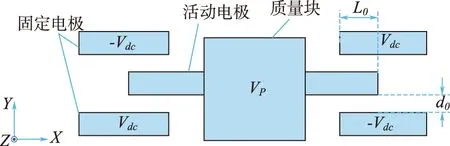
图2 静电矫正电极示意图Fig.2 The scheme of electrostatic-forcesuppression electrodes
假设电极为理想平行板电极。在该电极排布形式下,质量块在运动状态下受到的y方向的静电力合力为
(4)
可以看出,静电力主要来源于质量块x和y方向的位移。当质量块静止且处于平衡位置时,y方向静电力合力为0;当质量块存在x或y方向位移时,在y方向将受到与位移成正比的静电力作用。矫正电极作用下陀螺检测模态的动态微分方程可以表示为
(5)
可以看出,刚度耦合误差kdsx可以通过调节静电力中与x成正比的项,从而得到抑制甚至抵消。
静电力矫正的目标在于消除检测模态动态方程中与驱动模态位移x相关的项,即令
(6)
2 陀螺静电矫正特性分析
在上述原理基础上,结合陀螺敏感结构及电极结构型式,对陀螺的静电矫正特性进行理论分析。
图3所示为一种电容式硅基微机电陀螺敏感结构示意图。结构采用典型的音叉结构,完全解耦型设计,梳齿型电容检测。结构设计频差在200Hz左右,中间质量块两侧分布静电矫正电极,通过在质量块和固定电极间施加偏压,能够对正交耦合误差实现静电力矫正。

图3 陀螺敏感结构示意图Fig.3 The scheme of sensing structure of the gyroscope
2.1 静电矫正特性静态分析
图4所示为敏感结构静电矫正电极的排布形式示意图。在这种排布形式下,静电力对刚度耦合的矫正作用可以表示为
(7)
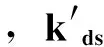

图4 静电矫正电极排布型式Fig.4 Configuration of the electrodes for electrostatic-force suppression
式(7)给出了静电矫正的原理分析公式。同时,在静态条件下,敏感结构质量块在静电力和刚度耦合的共同作用下存在受力平衡方程
(8)
整理得到静电矫正特性表达式
(9)
由式(9)可知,静态条件下结构的耦合位移比与静电矫正电压之间为线性关系。当静电矫正电极的静电力恰好能够抵消由kds带来的刚度耦合误差源时,结构静态耦合位移比为0,此时正交耦合误差能够得到很好的抑制。
2.2 实测数据与静态特性的转换关系
实际陀螺结构工作在谐振状态下,对陀螺正交耦合误差的测试也是在动态条件下进行,通常采用检测和驱动模态的振幅比——耦合位移比,作为表头正交耦合误差的测试结果。
通过式(3)可知,动态条件下,驱动和检测模态的耦合位移比可以表示为
(10)
通过转换运算,可以得到实测耦合位移比与静态刚度耦合系数比之间的转换关系,如式(11)所示。
(11)
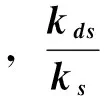
3 有限元仿真
在上述分析过程中,对静电力的计算均基于理想平行板电极的假设展开。实际静电矫正电极为梳齿电极,通常难以简化为理想平行板电极。因此,通过理论计算难以对陀螺敏感结构的静电矫正能力进行分析,下面将使用有限元分析软件对结构静电矫正能力进行分析计算。
使用有限元仿真软件ANSYS对敏感结构的静电矫正特性进行仿真分析,涉及结构和静电两种物理场的耦合分析。在ANSYS软件中,结构—静电的耦合分析有多种方法可以实现[7],综合模型建立、分析精度、计算速度等因素,选择直接耦合法对敏感结构的静电矫正特性进行有限元仿真分析。
3.1 敏感结构误差模型
刚度耦合的主要来源在于敏感结构中关键梁的加工误差,包括梁截面误差、对称性误差等。理想情况下,使用完全解耦设计的陀螺敏感结构其耦合位移接近于0。为模拟实际加工过程带来的耦合误差,可以对理想模型的关键梁参数进行修改。
图5所示为敏感结构中的两个关键梁,通过修改关键梁的尺寸参数,能够在理想模型中引入不对称因素,从而实现对刚度耦合的模拟。

图5 敏感结构的关键梁示意图Fig.5 The scheme of the keybeams in the sensing structure
实际陀螺敏感结构的刚度耦合系数比可以通过测试得到,对20支陀螺表头进行刚度耦合系数比测试,并计算得到统计均值。
通过对关键梁参数进行修改,使得有限元模型的刚度耦合系数比与实测均值相近。表1给出了关键梁参数的修改量。

表1 关键梁参数修改量Tab.1 Modification of the dimensions of the key beams
表2给出了修改后误差模型的刚度耦合系数比与实测均值的对比情况。
表2 实测均值与误差模型的刚度耦合系数比
Tab.2 Quadrature error coefficient ratio of the average measured value and the imperfect model
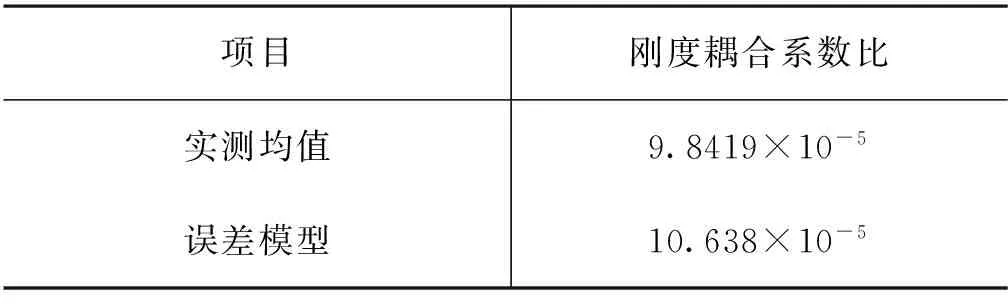
项目刚度耦合系数比实测均值9.8419×10-5误差模型10.638×10-5
通过修改关键梁参数,使得修改后的有限元模型的刚度耦合系数比与实测均值相近,并以此误差模型作为后续有限元仿真的主体结构模型。
3.2 敏感结构耦合场有限元模型
敏感结构的耦合场有限元模型主要由敏感结构主体模型及极板间气隙模型两部分组成。其中,结构主体模型采用三维实体单元SOLID95,极板间气隙模型采用三维实体直接耦合单元SOLID226。
矫正电极位置处的有限元模型的局部放大图如图6所示。图6中,蓝色部分为主体结构单元,红色部分为极板间气隙单元。单元间通过共用节点实现连接。
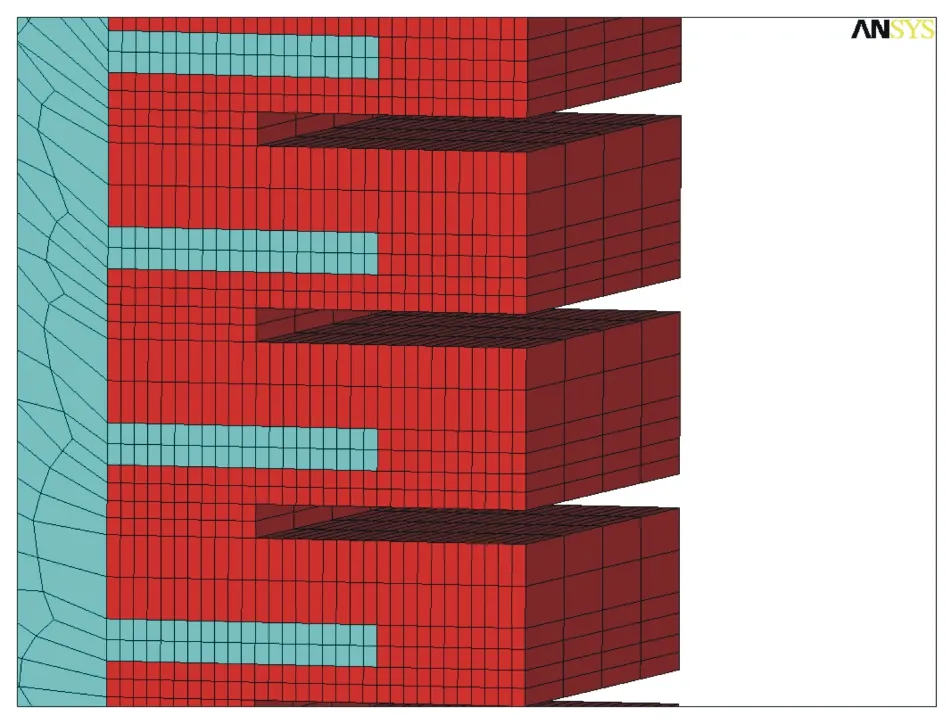
图6 有限元模型局部图Fig.6 Partial view of the multi-field FEM model
通过式(7)可以看出,在矫正电极的尺寸参数中,电极间距d对静电矫正特性的影响最大。因此,在某批次芯片中随机抽取三片进行敏感结构静电矫正电极的间距参数测量。在每片敏感结构上选取10个位置分别对梳齿的极板间距进行测量,对三片共30个极板间距尺寸的测量结果进行统计,结果如表3所示。

表3 电极间距尺寸实测数据统计Tab.3 Statistical data of the measured d dimension
调节有限元模型的极板间距参数,分别取设计值4μm、均值5.6389μm、分布范围的边界值5.227μm、6.0508μm,建立敏感结构的耦合场有限元模型。
3.3 仿真结果
使用ANSYS软件耦合场计算工具multiphysics对3.2节中建立的敏感结构误差模型进行静电—结构耦合场静态分析。采用耦合场分析方法中的直接耦合法进行多物理场耦合分析,通过载荷向量和网格随动,实现静电载荷和结构位移间的耦合计算。
在结构模型上施加10V恒定直流偏压,改变静电矫正电极上的直流电压值,对4个间距d取值下的有限元模型进行耦合场静态分析。得到调频电极间距取上述4个值时,结构的静电矫正特性曲线,如图7所示。

图7 静态耦合位移比随静电矫正电压变化曲线Fig.7 Linear relationship curve betweenstatic quadrature error and suppression voltage
图7给出了不同电极间距下的结构静电矫正特性曲线的斜率对比。
对比不同电极间距下的结构静电矫正特性曲线斜率,可以得出结论:
1)考虑实际静电矫正电极间距加工误差,取实测间距的1σ分布范围,可以得到陀螺静电矫正特性曲线斜率的分布范围为:[1.0024×10-5,1.5848×10-5];
2)加工过程导致静电矫正电极间距与设计值之间的误差,对结构静电矫正特性影响很大,实际结构的静电矫正能力较结构设计值偏小。
4 实验结果
为验证上述仿真分析的正确性,选择一支封装完成的陀螺表头进行静电矫正特性测试实验。
经初步测试,得到表头矫正前的耦合位移比及耦合刚度系数比,如表4所示。

表4 陀螺表头耦合误差实测数据Tab.4 Measured data of the coupling error
在此基础上,对该陀螺表头进行静电矫正实验。将测试数据拟合,得到陀螺表头的静电矫正特性曲线,如图8所示。

图8 陀螺实测静电矫正特性曲线Fig.8 Characteristic curve of the electrostatic suppression test
拟合得到陀螺表头的静电矫正特性曲线斜率值,如表5所示。

表5 陀螺表头实测数据拟合结果
对比表5中数据可知,实测结果落在仿真范围以内,可以认为仿真分析得到的静电矫正特性斜率范围具有一定的正确性,与陀螺的实际静电矫正能力相吻合。
依照仿真得到的斜率取值范围,可以给出结构所需静电矫正电压范围的计算公式
(12)
式中:ke1=1.0024×10-5,ke2=1.5848×10-5。
采用式(12)所示的计算方法,对上述陀螺表头进行静电矫正电压估算,估算结果与实测数据如表6所示。

表6 静电矫正电压实测与估算范围对比Tab.6 Comparison of the suppressionvoltage between test and calculation
表6中的数据显示,实际陀螺的静电矫正电压在式(12)提供的估算范围以内,可以认为该公式具有一定的正确性。
5 结论
本文借助有限元软件ANSYS对硅基平面振动式音叉陀螺正交耦合误差的静电力抑制开展有限元仿真分析。通过理论分析,确定敏感结构静电矫正特性的描述方式,并建立实测数据与仿真分析之间的对应关系;结合对实际加工情况的测量和统计,建立敏感结构误差模型和耦合场有限元模型,并在此基础上进行仿真分析,得到静态条件下的静电矫正特性曲线及曲线斜率范围;最后通过实物测试,验证了仿真结果的正确性。
对敏感结构静电矫正特性的仿真分析,对陀螺敏感结构矫正电极的改进设计、控制电路设计、表头筛选测试等后续工作具有重要的参考价值。
[1] Jae Yoong Cho.High-performance micromachined vibratory rate-and rate-integrating gyroscopes[D].United States:University of Michigan,2012.
[2] W Geiger,B Folkmer,U Sobe,H Sandmaier,W Lang. New designs of micromachined vibrating rate gyroscopes with decoupled oscillation modes[J]. Sens. Actuators A,Phys.,Apr.1998,66(1-3):118-124.
[3] W Geiger,W U Butt,A Gainer,J Frech,M Braxmaier,T Link,A Kohne,P Nommensen,H Sandmaier,W Lang.Decoupled microgyros and the design principle DAVED[J]. Sens. Actuators A,Phys.,Jan.2002,95(2/3):239-249.
[4] William A Clark,Roger T Howe.Surface micromachined Z-axis vibratory rate gyroscope.Solid State Sensor and Actuator Workshop,Hilton Head,USA,June,1996.
[5] E TATAR.Quadrature error compensation and its effects on the performance of fully decoupled MEMS gyroscopes[D].Turkey:Middle East Technical University,2010.
[6] M S Weinberg,A Kourepenis.Error sources in in-plane silicon tuning-fork MEMS gyroscopes[J].Journal of Microelectromech-nical System, Jun.2006,15(3):479-491.
[7] 党沙沙,许洋,张红松.ANSYS 12.0 多物理耦合场有限元分析从入门到精通[M].北京:机械工业出版社,2010,1-5.
The FEM Analysis of Electrostatic-force Suppression of Quadrature Coupling Error in a MEMS Gyroscope
DOU Mao-lian,LIU Fei,LIN Meng-na,GUO Zhong-yang
(Beijing Institute of Automatic Control Equipment,Beijing 10074,China)
As an sensing mode output deviator caused by stiffness coupling between vibration modes of sensing structures,quadrature coupling error is one of the key error sources that influence the performance of a MEMS gyro.Electrostatic-force suppression,using DC voltage to adjust the misalignment of the mode principle axis,is one of the most effective ways to eliminate quadrature coupling error,which has on-chip and real-time adjustment capability.Based on the theory and FEM analysis of electrostatic-force suppression,this paper demonstrates detailedly the FEM analysis for a typical silicon tuning fork gyro and the experimental verifications of this analysis.
MEMS gyroscope;Quadrature coupling error;Electrostatic-force suppression;FEM simulation
2015 - 03 - 02;
2015 - 03 - 24。
窦茂莲(1991 - ),女,硕士,助理工程师,主要从事微机械陀螺方面的研究。
E-mail:doumaolian5@163.com
V444
A
2095-8110(2015)05-0052-06
