沥青混合料单轴贯入抗剪试验的细观分析*

颜可珍，葛冬冬，游凌云

(湖南大学 土木工程学院，湖南 长沙 410082)

沥青混合料单轴贯入抗剪试验的细观分析*

颜可珍†，葛冬冬，游凌云

(湖南大学 土木工程学院，湖南 长沙 410082)

单轴贯入试验可以有效地测试沥青混合料的剪切强度，通过建立沥青混合料单轴贯入试验的颗粒流模型，分析了沥青混合料的抗剪作用机理. 基于颗粒流的细观机理，采用离散元技术对沥青混合料单轴贯入试验进行细观模拟，得到了沥青混合料单轴贯入时的应力应变曲线变化规律，并将模拟结果进行了验证，揭示了沥青混合料单轴贯入试验的细观机理. 分析了贯入速率、压头直径及试件尺寸等对试验结果的影响规律，在此基础上提出了合适的试验技术参数，为贯入试验提供技术参考. 结合单轴贯入试验和无侧限抗压强度试验，提出了基于离散单元法确定沥青混合料抗剪参数的方法，并为采用细观分析方法探究混合料性能提供了一种思路.

道路工程；单轴贯入试验；离散单元法；沥青混合料；模拟

近年来，中国沥青路面早期破坏现象较为严重，车辙已成为沥青路面的主要病害之一. 车辙主要是由于沥青混合料在剪应力作用下产生塑性流动的结果，在轮载作用下，路面面层产生较大的水平剪应力，特别在高温环境下沥青混合料的抗剪能力下降，使沥青路面容易出现较为严重的车辙现象[1]. 然而，目前中国的沥青路面设计尚未很好地考虑这种剪切破坏，也无明确的沥青混合料抗剪强度测试方法. 沥青混合料抗剪强度的确定主要是利用经验的设计方法或三轴试验. 有研究表明，三轴试验的应力分布与实际路面有一定差异，且试验过程较为复杂.毕玉峰等[2]提出了利用单轴贯入试验测定沥青混合料抗剪切特性的方法，该试验试件内剪应力分布与实际路面在车载作用下的剪应力分布相似，试验过程中压头周边材料对压头下圆柱体形成侧向水平约束，试件破坏意味着约束的破坏，反映了沥青混合料抗剪强度的形成机理. 该方法虽然从宏观上获得沥青混合料的剪切强度，但沥青混合料的贯入强度机理尚不十分明确，贯入过程中混合料颗粒间的相互作用有待进一步深入研究.

基于颗粒流的离散单元法是近年发展起来的细观数值分析方法，在模拟沥青混合料性能方面得到了较为广泛的应用，成功地克服了有限元法不能反应颗粒间相互作用的缺陷. You等[3-4]采用离散单元法研究沥青混合料的粘弹性特性. Wu等[5]应用离散单元法成功模拟了了理想沥青混合料的等速率应变压缩试验. Liu等[6]采用离散元程序模拟了沥青混合料的重复加载试验. Mahmoud等[7]用离散元方法研究了集料性质和内部结构对沥青混合料性能的影响. 冯师蓉等[8]用离散元模拟了沥青混合料的蠕变过程. 王端宜等[9]用离散元模拟了沥青混合料的单轴压缩过程. 汪海年等[10]研究了橡胶热再生混合料低温性能的细观特征. 离散单元法为研究沥青混合料的细观行为提供了一种新的思路，鉴于此，本文将基于颗粒流原理对沥青混合料单轴贯入试验进行细观模拟，从细观上研究沥青混合料单轴贯入的试验条件影响，并结合无侧限抗压强度试验结果提出基于离散单元法确定混合料抗剪参数的方法，为确定沥青混合料的抗剪强度提供技术指导.

1 离散元基本理论

离散单元法(Discrete Element Method，DEM)是研究非连续介质力学行为的一种计算方法，它的基本原理是将散粒体离散成独立单元的集合，利用牛顿第二定律建立每个单元的运动方程，再用动态松弛法迭代求解，从而求得散粒体的整体运动形态.

1.1 模型假设

颗粒流(Particle Flow Code， PFC)是简化的离散元方法，它通过模拟圆形颗粒的运动及其相互作用来研究颗粒介质的特性. 该方法在模拟过程中作了如下假设：①颗粒单元为刚性体；②接触发生在很小的范围内，即点接触；③接触特性为柔性接触，接触处允许有一定的重叠；④重叠量与接触力有关，与颗粒尺寸相比，重叠量很小；⑤接触处允许粘结存在；⑥颗粒单元为圆形.

1.2 计算循环过程

颗粒流方法每一次循环包括以下2个主要计算步骤：

1)由作用力、反作用力原理和相邻颗粒间的接触本构关系确定颗粒间的接触力和相对位移．

2)由牛顿第二定律确定由于相对位移而产生的新不平衡力，直至要求的循环次数或颗粒移动趋于稳定或颗粒受力趋于平衡.

其计算流程如图1所示. 介质力学应满足运动方程(牛顿第二定律)和物理方程(力-位移定律)，它们的公式分别为：

(1)

Fn=KnUn,

(2)

ΔFs=KsΔUs，

(3)

Fs←Fs+ΔFs≤μFn．

(4)

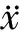
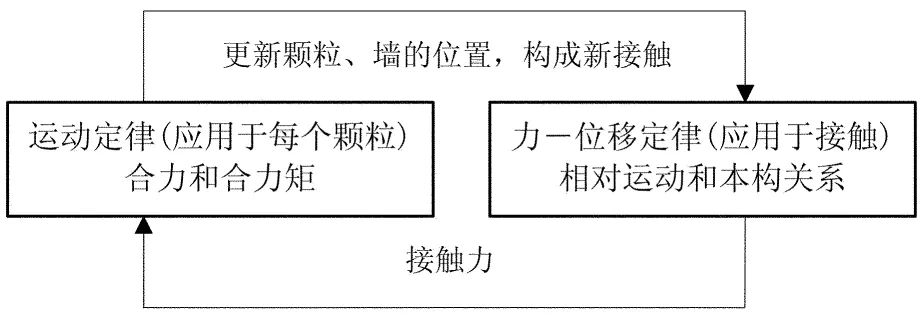
图1 离散单元法的计算流程

沥青混合料PFC3D模拟时间过长,且受电脑计算水平的限制,陈渊召等[11]使用PFC2D对沥青混合料的细观结构进行分析且得到了较好的效果,本文也将使用PFC2D对沥青混合料抗剪试验方法进行模拟.

2 单轴贯入试验模型的建立

单轴贯入试验类似于土工试验方法中的CBR试验，其原理就是在试件上通过钢压头进行加压，压头的直径小于试件的直径，来模拟路面在荷载作用下的实际受力情形[2].

2.1 单轴贯入试验模型生成

为了实现沥青混合料单轴贯入试验的数值模拟，首先建立沥青混合料试验试件的细观模型. 定义四道墙体单元，在生成的墙体范围内生成颗粒，颗粒由单位厚度的圆盘模拟. 对于沥青混合料，采用JTGD50-2006《公路沥青路面设计规范》推荐的AC20级配中值，颗粒级配表如表1所示. 分别将每一档集料向给定区域内按粒径范围由大到小随机填充，每档料的颗粒数目N按下式计算：

(5)

(6)

表1 颗粒级配表

颗粒模型生成时，先将颗粒进行等比例缩小，颗粒全部生成后再根据孔隙率进行放大. 但在颗粒放大过程中颗粒接触处常常会产生颗粒重叠现象，进而引起附加应力，影响模型的收敛. 为了消除这种不良影响，开始循环后，每隔一定时步将颗粒速度归零，使附加应力逐渐耗散. 当重叠消失、颗粒彼此分离后，再令集料颗粒正常收敛到各向同性应力的平衡状态.

本模型中添加平行粘结接触以模拟混合料中沥青的胶结作用，而DEM中颗粒间只有存在重叠接触才可以生成粘结接触，建模过程中不可避免会出现一些漂浮颗粒，即与其他颗粒接触数小于3的颗粒，为了避免模型中出现类似的粘结“空洞”[12]，在生成颗粒后通过调用函数对颗粒接触进行判断. 对那些接触数小于3的颗粒粒径进行稍微放大(通常为1%)，放大后要循环一定的时步，以使模型重新达到平衡，并且保持较小的各向同性应力. 最终生成的颗粒试件如图2(a)所示，颗粒初始应力分布如图2(b)所示(其中线条的粗细代表应力的大小).

2.2 模型参数的选择

颗粒流模拟可通过细观尺度颗粒之间的相互作用来反映宏观尺度沥青混合料整体的力学特性. 而离散元细观参数常常是未知的，并且无法通过现有物理试验方法直接测量. 本论文选择与试验试件级配一致的数值模型的级配，在室温条件下进行单轴贯入试验，并通过单轴贯入试验数值模拟的多次试算和调整，对参数进行拟合得到的沥青混合料的计算参数如表2所示，该参数模拟结果与试验结果具有较好的一致性(如图3所示).

图2 沥青混合料的PFC2D仿真试件

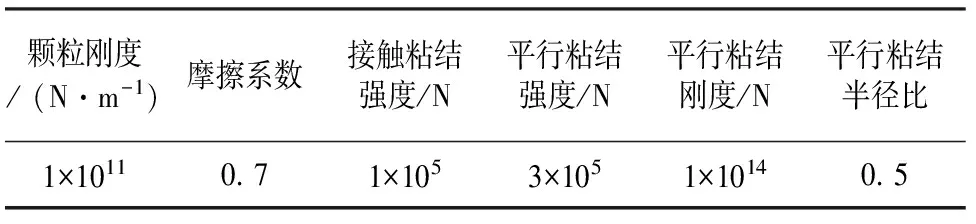
表2 细观接触本构参数

2.3 模拟变量的监测

通过在试件内设置测量圆可以获取应力场，测量圆之间均相切. 选择测量圆半径时主要权衡两方面因素：1)保证圈内一定颗粒数以减小因统计带来的随机误差；2)大尺寸测量圆导致的过度平均化不利于揭示区域内的规律. 通过在测量圆内调用内置函数计算其内部的平均应力张量和平均应变张量，而获得相应区域的平均应力和平均应变.

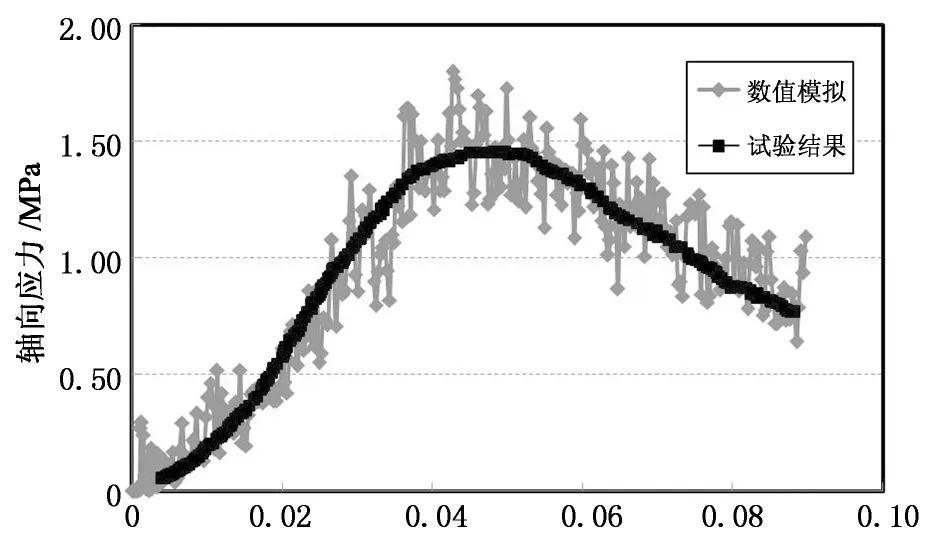
轴向应变

3 单轴贯入试验条件分析

3.1 贯入速度的影响分析

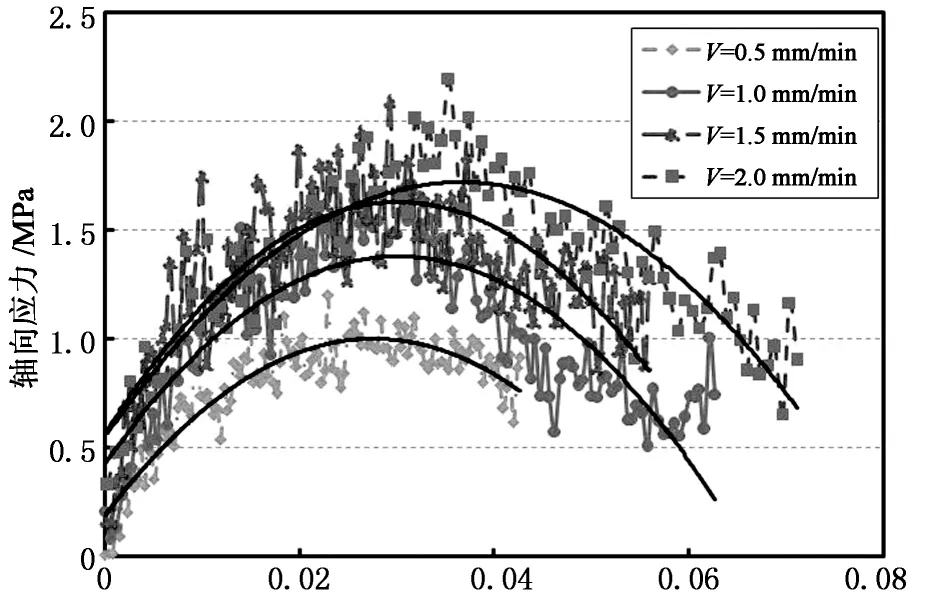
本节从不同贯入速度下沥青混合料抗剪强度的变化趋势和应力应变的规律出发，研究不同贯入速度(0. 5,1.0,1．5和2.0 mm/min)对试验结果的影响. 不同贯入速度下的剪应力峰值如表3所示. 不同贯入速度下的应力应变曲线颗粒流模型模拟结果如图4所示.

表3 贯入速度对沥青混合料抗剪强度的影响

由表3和图4可知，随着贯入速度的增加，沥青混合料试件的轴向应变和轴向应力增加，剪应力峰值随着贯入速度的增加呈线性增长的趋势，加载速度超过1．0 mm/min以后贯入应力峰值增大效果不明显. 对于道路实际受力状态，在不考虑其他环境因素的条件下，车速愈快，道路的力学响应愈好，车辆静止时荷载对路面结构的作用状态是路面结构的最恶劣受力状态. 为了兼顾与传统抗剪试验的可比性，在对比分析数值模拟结果与室内试验结果后，单轴贯入试验贯入速度取1．0 mm/min.

3.2 压头尺寸影响分析

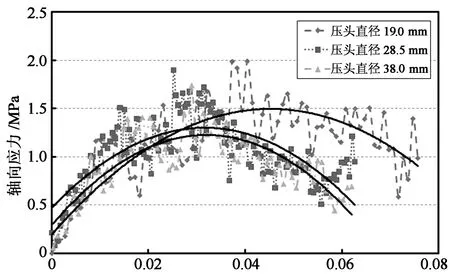
对于AC-20级配沥青混合料，公称最大粒径为19.5 mm，本研究选择压头直径分别为19.0，28.5和38.0 mm，分别为公称最大粒径的1倍，1．5倍和2倍，分析压头尺寸对沥青混合料单轴贯入数值试验的影响. 不同压头尺寸下的应力应变曲线颗粒流模型模拟结果如图5所示.

轴向应变

轴向应变

从图5可以看出，对于3种不同直径的压头，轴向应力大致都在轴向应变为0.035左右达到峰值，且轴向应力峰值随着压头直径的增加而降低. 为了进一步分析，本文给出了不同压头直径时虚拟试件的细观位移矢量场颗粒流模型模拟结果，如图6所示，其中箭头指向代表颗粒移动方向，箭头长度代表位移大小，长度越长，位移越大.

从图6可以看出，压头直径为38.0mm时，压头对试件影响已接近试件下部，且在压头作用下试件上部产生明显的侧向移动，在试件边缘仍有较大的位移，即压头直径过大，试件不能提供足够的侧向支撑. 而压头直径分别为28.5 mm和19.0 mm作用下，集料并无较大的侧向移动，说明该尺寸直径可以满足单轴贯入试验条件要求. 考虑图4中压头直径为19.0 mm应力应变曲线达到应力峰值后应力下降规律与压头直径分别为28.5 mm和38.0 mm的应力下降规律偏差较大，所以推荐压头直径取公称最大粒径的1.5倍 (28.5 mm) .

图6 不同压头直径作用下的试件细观位移场

3.3 试件尺寸影响分析

为了分析试件尺寸对沥青混合料单轴贯入数值试验的影响，针对相同的压头直径(28.5 mm)，本节考虑使用不同的试件尺寸，其中包括H×D=100 mm×100 mm(试件A)，H×D=100 mm×150 mm(试件B)，H×D=63.5 mm×100 mm(试件C).

本节从细观角度探讨了试件尺寸对细观位移场的影响，并讨论分析了不同尺寸条件下的贯入试验应力应变规律. 不同尺寸试件条件下，贯入试验细观位移状态颗粒流模型模拟结果如图7所示.

H×D=63.5 mm× 100 mm尺寸试件在试件底部仍有较大的位移与接触力，说明该试件高度不足，导致了试件底部颗粒位移较大而与试件底部支撑板发生明显作用. 试件高度大于100 mm后，试件底部的位移矢量呈现点状分布，压头对更底层颗粒作用已经可以忽略. 对比试件直径100 mm与150 mm发现，试件直径超过100 mm后，试件侧边颗粒位移矢量呈点状分布，100 mm直径已可为试件提供足够的侧向支撑. 对比不同尺寸试件数值模拟结果，发现H×D=100 mm×100 mm尺寸试件可满足试验要求.

图8为不同尺寸试件的应力应变曲线颗粒流模型模拟结果. 从图中可以看出应力应变曲线遵循大致相同的规律，由于试件高度不同在达到应力峰值时的应变不同.H×D=63.5 mm ×100 mm尺寸试件应力峰值较小，由于该试件高度不足影响了试验结果，其余两组试件应力峰值大致相同，表明直径100 mm可满足试验要求.

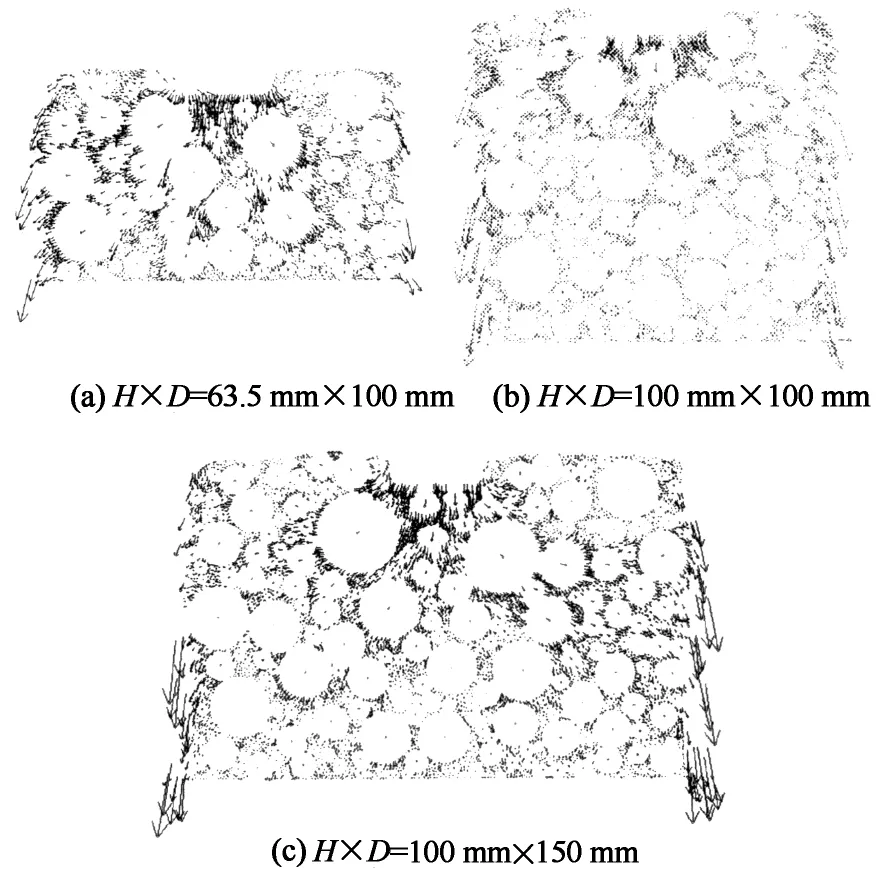
图7 不同尺寸试件的细观位移场

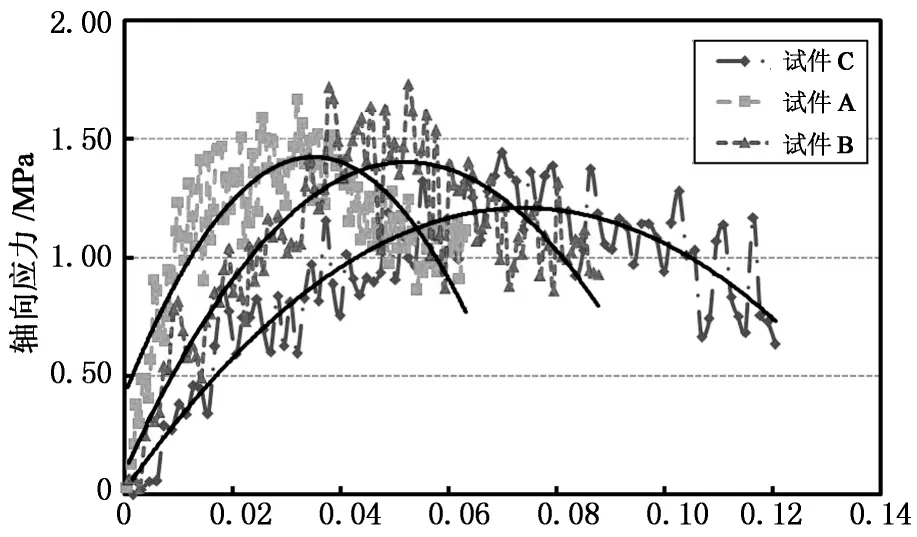
轴向应变

图4～图8是使用颗粒流对单轴贯入试验条件进行分析的结果，从细观角度分析了贯入速率、压头直径及试件尺寸对试验结果的影响规律，验证使用颗粒流建立沥青混合料单轴贯入试验的可行性，提供了一种从细观角度分析贯入试验机理的方法.

4 剪切强度的确定方法

孙立军在提出单轴贯入试验确定沥青混合料的抗剪切强度时，建立了与实际试验对应的有限单元法模型来进行剪切计算，提出了明确的剪切参数，并利用贯入试验抗剪强度数据，求解出混合料的抗剪参数如表4所示.

表4 有限元计算的基本抗剪强度参数

前人研究倾向于建立最大剪应力与压头轴向应力的关系，这是由于室内试验无法精确得到试件中的最大剪应力，但可通过试验机获得压头的轴向应力. 而利用单轴贯入离散元模拟，可以直接得到模型中的最大剪应力，但模拟结果的精确性受到测量圆布置位置、测量圆尺寸等方面的限制. 为了提高贯入试验模拟的精度，可以通过建立大量加载模型，分析比较多个模拟试验结果，进而建立单轴贯入试验最大剪应力与其他试验数据的关系.

为了确定沥青混合料的抗剪参数C和φ，需要同时进行单轴贯入试验与无侧限抗压强度试验.

4.1 无侧限抗压强度试验模拟

以固定的速度竖直向下推进上加载板，以模拟虚拟试件压缩破坏的过程，同时监测加载板的位移接触力变化规律. 该试件的压应力与压缩位移的关系曲线(即抗压强度曲线)如图9所示. 试件破坏时的细观位移场和颗粒间接触力状态如图10所示.

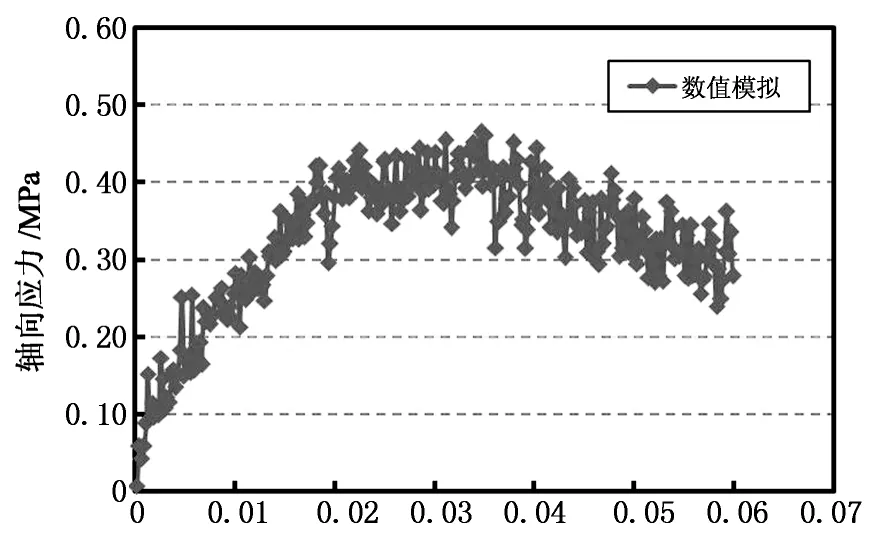
轴向应变

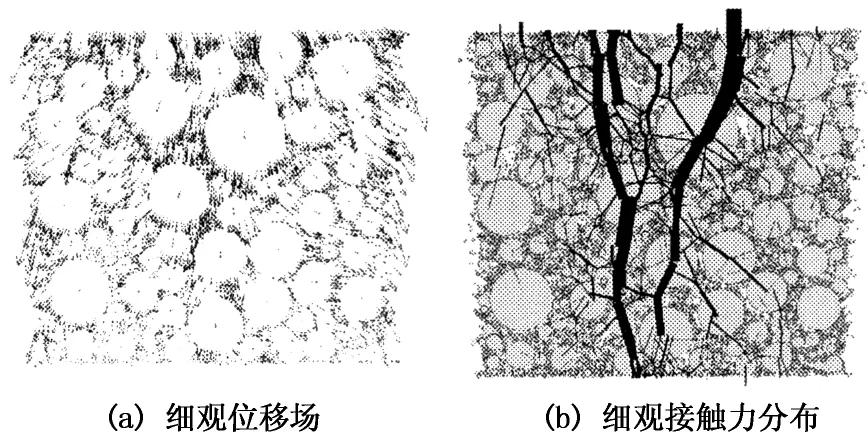
图10 无侧限抗压试验细观矢量场

从细观位移场分布可以看出，在模型试件上部，颗粒出现整体向下移动现象，且位移大小大致相同. 与单轴贯入试验相比，无侧限抗压强度试验中间颗粒移动并未出现集中现象. 但是颗粒间接触力分布在中间分布较为集中，这是由于中间颗粒受到边缘颗粒的限制，竖向传递荷载能力较强，而侧边颗粒由于侧向限制较小，其传递荷载能力较中间颗粒弱.

4.2 抗剪参数C和φ的确定

本研究尝试通过离散单元法建立与室内试验类似的贯入模型，并通过设置测量圆获得试件中剪应力最大位置的主应力值，即得到了试件中剪应力最大处的各主应力值和剪应力峰值. 与此同时，进行了无侧限抗压强度试验模拟，根据这两组试验数据，得出莫尔应力圆以求解出沥青混合料的粘聚力C和内摩擦角φ.

图11为利用单轴贯入试验和无侧限抗压试验的数据结果得到的莫尔应力圆，图中，σu为无侧限抗压试验试件的抗压强度，σ1和σ3为单轴贯入试验测量圆获得的主应力值，则图中的C和φ就是混合料的粘聚力和内摩擦角.

图11 试验的莫尔圆图示

利用简单的数值几何关系，可以推导得出基于单轴贯入试验和无侧限抗压强度试验的C和φ公式为：

(7)

由式(7)可以求解出C和φ值：

(8)

通过式(8)，就可以利用由离散单元法建立的单轴贯入试验和无侧限抗压强度试验测得的强度，求解出沥青混合料的粘聚力C和内摩擦角φ.

4.3 试验对比分析

本文选用与试验模拟相同的级配并使用相同的试件尺寸与压头直径进行室内试验，对比模拟结果与试验结果并计算相应参数误差如表5所示. 沥青混合料的粘聚力C受温度影响较大，实验误差与模拟结果误差较大，而内摩擦角和剪应力值误差较小，证明了模拟结果的可靠性. 通过试验结果与模拟结果的对比验证了从细观角度分析试验方法的合理性，该方法可从细观角度修正试验方法.

表5 模拟结果与试验结果对比

5 结 论

1) 本文基于离散元原理模拟分析了沥青混合料的单轴贯入试验，分析了单轴贯入试验的应力应变及剪应力分布规律，从细观角度表明了单轴贯入试验能很好地表征沥青混合料的剪切机理.

2) 对比分析了贯入速率、压头直径及试件尺寸对沥青混合料贯入过程的应力应变及剪应力影响规律. 建立压头直径与公称最大粒径的关系，为不同级配混合料采用不同的试验条件提供一种思路.

3) 离散单元法可以建立沥青混合料宏观和微观两个层面的联系，较好地模拟研究沥青混合料的力学性能. 提出了基于离散单元法评估沥青混合料抗剪强度并确定抗剪参数的方法.

[1] 孙立军．沥青路面结构行为理论[M]．北京：人民交通出版社，2005：309-312.

SUN Li-jun.Structure behavior study of asphalt pavements[M].Beijing: China Communication Press, 2005：309-312. (In Chinese)

[2] 毕玉峰, 孙立军．沥青混合料抗剪试验方法研究[J]．同济大学学报:自然科学版,2005，33(8):1036-1040.

BI Yu-feng , SUN Li-jun. Research on test method of asphalt mixture’ s shearing properties [J].Journal of Tongji University：Natural Science, 2005,33(8): 1036-1040.(In Chinese)

[3] LIU Yu, DAI Qing-li, YOU Zhan-ping. Viscoelastic model for discrete element simulation of asphalt mixtures[J]. Journal of Engineering Mechanics,2009, 135(4):324-333.

[4] YOU Zhan-ping, LIU Yu, DAI Qing-li. Three-dimensional microstructural-based discrete element viscoelastic modeling of creep compliance tests for asphalt mixtures[J]. Journal of Material in Civil Engineering, 2011,23(1):79-87.

[5] WU Jun-wei, COLLOP ANDREW C, MCDOWELL GLENN R.Discrete element modeling of constant strain rate compression tests on idealized asphalt mixture[J]. Journal of Material in Civil Engineering, 2011, 23 (1): 2-11.

[6] LIU Yu, YOU Zhan-ping. Simulation of cyclic loading tests for asphalt mixtures using user defined models within discrete element method[C]//Geo Congress. New Orleans:ASCE, 2008: 742-749.

[7] MAHMOUD E, MASAD E, NAZARIAN S.Discrete element analysis of the influences of aggregate properties and internal structure on fracture in asphalt mixtures[J]. Journal of Material in Civil Engineering, 2010,22(1):10-20.

[8] 冯师蓉, 胡霞光, 刘玉.粘弹性材料的离散元数值分析[J].公路交通科技, 2008(2): 12-29.

FENG Shi-rong, HU Xia-guang, LIU Yu.Numerical analysis of viscoelastic materials based on discrete element method [J].Journal of Highway and Transportation Research and Development, 2008( 2): 12- 29. (In Chinese)

[9] 王端宜,赵熙.沥青混合料单轴压缩试验的离散元仿真[J].华南理工大学学报:自然科学版, 2009,37(7): 37-41.

WANG Duan-yi,ZHAO Xi.Simulation of uniaxial compression test for asphalt mixture with discrete element method [ J]. Journal of South China University of Technology：Natural Science Edition, 2009,37( 7): 37-41.(In Chinese)

[10]汪海年，张琛，方俊，等.橡胶热再生混合料低温性能与细观特征研究[J].湖南大学学报:自然科学版, 2014,41(11): 123-128.

WANG Hai-nian, ZHANG Chen, FANG Jun,etal.Study on low temperature performance and microstructure of rubber hot recycled mixture [J].Journal of Hunan University:Natural Sciences, 2014, 41 (11): 123-128.(In Chinese)

[11]陈渊召，李振霞.基于离散元法的橡胶颗粒沥青混合料细观结构分析[J].哈尔滨工业大学学报, 2013,45(4): 116-121.

CHEN Yuan-zhao, LI Zhen-xia.Meso-structure of crumb rubber asphalt mixture based on discrete element method [J].Journal of Harbin Institute of Technology, 2013,45(4): 116-121.(In Chinese)

[12]LEE York-wei.Discrete element modeling of idealized asphalt mixture[D].Nottingham: University of Nottingham,2006.

Microscopic Analysis of Asphalt Mixture Uniaxial Penetration Shear Test

YAN Ke-zhen†, GE Dong-dong, YOU Ling-yun

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China )

Uniaxial penetration experiments can test the shear strength of asphalt mixture effectively. In this paper, the shear mechanism of asphalt mixture was analyzed by establishing a particle flow model of asphalt mixture uniaxial penetration test. Based on the microscopic mechanism of particle flow，this paper used discrete element technique to microscopically simulate the uniaxial penetration test of asphalt mixture. The stress-strain curve of the mixture was obtained, the simulation results were validated, and then, the microscopic mechanism of the asphalt mixture in the uniaxial penetration test was revealed. This paper analyzed the effect of the penetration rate, pressure head diameter and specimen size on the test results and proposed appropriate test technical parameters based on this, which provides technical reference for the penetration test. Combined with uniaxial penetration test and unconfined compressive strength test, a method based on discrete element method to determine the asphalt mixture shear parameters was proposed. A method was provided to explore the properties of asphalt mixture by adopting the micromechanical analysis method.

pavement engineering; uniaxial penetration test; discrete element method; asphalt mixtures; simulation

1674-2974(2015)05-0113-07

2014-08-22

国家自然科学基金资助项目(51278188), National Natural Science Foundation of China(51278188)；湖南大学“青年教师成长计划”资助项目；湖南省普通高校青年骨干教师培养计划资助项目

颜可珍(1975-)，男，湖南桃江人，湖南大学教授，博士

†通讯联系人，E-mail: yankz@hnu.edu.cn

U414

A