地震强度递增沙堆模型响应机制的研究*

郭海强，姚令侃,2,3†，郭沉稳，黄艺丹

(1.西南交通大学 土木工程学院，四川 成都 610031；2.高速铁路线路工程教育部重点实验室， 四川 成都 610031；3.抗震工程技术四川省重点实验室道路与铁道工程抗震技术研究所，四川 成都 610031)

地震强度递增沙堆模型响应机制的研究*

郭海强1，姚令侃1,2,3†，郭沉稳1，黄艺丹1

(1.西南交通大学 土木工程学院，四川 成都 610031；2.高速铁路线路工程教育部重点实验室， 四川 成都 610031；3.抗震工程技术四川省重点实验室道路与铁道工程抗震技术研究所，四川 成都 610031)

针对汶川地震Ⅹ度和Ⅺ度烈度区崩塌滑坡面积与累计频率统计关系呈现不同分布规律的现象，开展了地震峰值加速度从0.075～0.450 g的6组振动台沙堆模型实验.实验重现了随振动强度增加，落沙量与累计频率从幂律分布-对数正态分布-正态分布依次转变的现象.数学分析表明，变异系数的减小，是这3种概型依次转变的原因.根据实验观察，随扰动递增沙堆表面颗粒行为呈现不同响应模式：微振动时颗粒活动性消失的概率与活动性分叉的概率在总体上平衡，当颗粒间近邻的相互作用导致连锁反应时才能发生大规模落沙事件，具有最大的不确定性.强振动时大部分颗粒就能独立启动，大规模落沙成为必然事件.据此提出，落沙规模由自组织控制的颗粒链式反应过程，向外力控制的颗粒独立下落过程的转化是导致变异系数减小的物理机制.根据以上认识，随地震烈度增加，汶川地震触发的崩塌滑坡规模与累计频率依次服从幂律分布-对数正态分布的现象，可能是具有普适性意义的规律.

地震；滑坡；自组织临界性；沙堆模型实验；变异系数

自组织临界状态(Self-organized Criticality，SOC)理论由Bak[1]首先提出，用以解释复杂系统的行为特性.Held等[2]第一次通过物理实验证明了沙堆具有自组织临界性.通过该实验发现当沙堆达到临界角附近时，落下的一粒沙，可能固定在沙堆上、也可能引起小范围沙粒滑动、还可能导致更大规模的“雪崩”，最终收集到的落沙量从零到数百粒不等，其落沙规模与频率服从幂律分布，至此沙堆模型就成为了研究SOC的范例，它反映了一种在自组织作用下的斜坡物质能量耗散普适性过程[3-5].运用SOC理论来研究地震诱发崩塌、滑坡的整体分布问题具有明显优势，既能从宏观把握它们的总体特征又能摆脱对单个崩塌、滑坡独特形成机理的限制性，进而得到具有普适性的规律.

Fuyii[6]在日本统计了650个由大雨造成的滑坡面积数据，并发现滑坡面积的量级-频率之间存在幂律分布的现象，随后几十年中，相继有学者发现有关于降雨及地震造成的滑坡量级-频率之间存在幂律分布关系[7-8]，但都关注于对幂指数b值大小的研究，缺乏对幂律分布机理进行解释.Yao等[9]针对四川地区滑坡、岩堆规模呈幂律分布的现象，提出了SOC形成机制的初步解释；但以上工作均未开展过物理模型实验.2008年5.12汶川大地震后，展开了运用SOC研究地震诱发崩塌滑坡整体分布的专题研究，如在汶川震后的抢险阶段，就开始对G213线都江堰至映秀段沿线由地震触发的崩塌体进行详查及测量，并发现位于Ⅸ度地震区的61个崩滑工点(数十方～数万方)，崩滑方量与崩滑工点数目之间存在着幂律关系[10].同时，利用离心模型开展了地震作用下的沙堆模型实验，发现斜坡堆积体(按照重力相似准则高度达20.4 m)在按照拟静力原理模拟的地震力扰动下(以沙堆模型底板倾斜1.5°模拟中震、模型底板倾斜3°模拟大震)，斜坡崩塌的动力学特性可以用幂律描述.据此首次提出斜坡系统在中、小地震下的崩塌规模呈现SOC效应，大震时服从正态分布等假设[11].但是受条件限制，在Ⅹ，Ⅺ度地震区，实测得到的统计样本数偏少，无法对高于Ⅸ度地震烈度区的统计结果得出准确的结论[10].同时，离心模型实验模拟的地震力与真实地震物理过程相距较大，所谓“中小震”的限制条件也过于笼统，因此若没有可被直接观察的地震触发崩滑现象作为研究条件，该假设面临如何检验以及崩塌滑坡服从SOC的判据如何量化等问题[11].

本文针对以上问题，做了进一步的研究.如依据卫星遥感影像，对位于汶川地震Ⅹ度区、Ⅺ度区崩坡体的面积进行了人工解译，获取了大量的统计样本，发现在Ⅹ度区，地震触发的崩滑面积与累计频率的关系仍为幂律关系，但关系减弱；Ⅺ度区，地震触发的崩滑面积与累计频率之间的关系服从对数正态分布.由此可知，随地震烈度增加，地震触发崩滑规模的整体分布规律会发生变化.若超越这些从统计层面获得的表观认知，能否从理论上证明随地震强度增加，斜坡系统的动力学特性转变具有普适性的意义？能否找到导致其动力特性转变的原因？如上问题急需得到理论上的解释.本文的目的即是在SOC的概念框架下，希望通过振动台沙堆模型实验，重现沙堆模型随地震扰动加强的动力学演变过程，并寻找斜坡系统动力学特性转变的原因.

1 振动台沙堆模型实验

沙堆模型是具有SOC性质的系统，在临界状态下即使是受到一系列微小的、均匀的扰动，其反应随时间的变化也很大，但每次扰动下表征反应规模的物理量可用幂律描述，故幂律可以作为SOC的证据，而与扰动方式无关，这就是沙堆模型实验的原理[5,11].

1.1 实验设计

振动台沙堆模型实验依托于高速铁路线路工程教育部重点实验室单向电液伺服驱动式地震模拟振动台开展，其主要技术指标如表1所示.

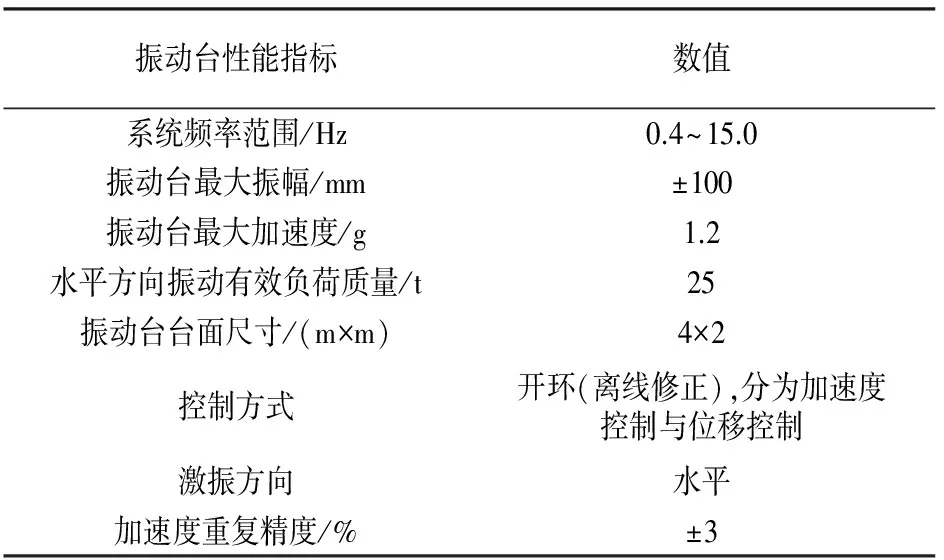
表1 振动台主要技术指标

由于地震触发造成的崩塌滑坡是规模差异巨大的灾害现象，小到数方就造成公路断道灾害的崩塌落石，大到上亿方的巨型滑坡(大光包滑坡估算体积约7.5亿m3)，并且没有特征尺度，所以在沙堆模型设计时并不强调对原型工点尺度的相似关系.本实验主要研究地震强度变化对沙堆模型动力学的影响，每次实验沙堆物理参数相同，这有利于进行对比分析，因此实验沙堆密度取1.658×103kg/m3、含水率为0.5%，并要求实验全程保持不变.沙堆填料选用G213线都江堰至映秀段某一典型地震触发崩塌工点粒径≤50 mm的天然干燥沙石，其级配比例如图1所示.在模型箱内加沙前，为消除钢制刚性模型实验箱侧壁的摩擦约束，在模型箱的两侧壁各粘贴一层透明薄膜来减小侧壁摩擦，且便于观察模型表观变形情况.在模型箱内加沙时，依靠沙石自身重力下滑形成自然坡面，当沙堆坡脚触及台面端边缘，直至加沙量与落沙量基本持平时，则沙堆达到天然临界休止角，此时为临界状态，如图2所示.该天然单面坡沙堆总质量为6.8 t，长258 cm，宽150 cm，高195 cm.

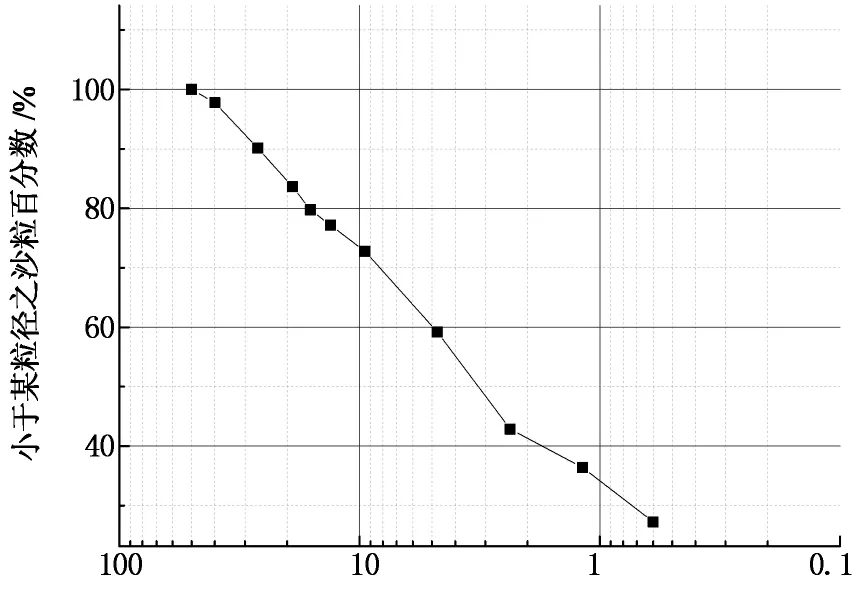
粒径/mm

图2 沙堆模型

实验输入的是汶川地震卧龙台站记录的修正波，根据原波的峰值加速度与设计的目标峰值加速度的比值，对卧龙台站记录的修正波幅值进行压缩，得到每组实验的地震波，共设计了地震峰值加速度(PGA)从0.075～0.450 g的6组实验.以称质量的方法称取每次地震波扰动后滑出台面的沙粒质量，用近景摄影测量技术获取沙堆体积的变化量及坡体表面动力学特征.

1.2 实验数据统计特征

振动台沙堆模型实验的假设检验结果如表2所示.沙堆随PGA增加呈现3种概率分布：1)当PGA=0.075～0.125 g时，样本经检验服从幂律分布.2)当PGA=0.15～0.25 g时，样本经检验服从对数正态分布.3)当PGA=0.35～0.45 g时，样本经检验服从正态分布.

振动台沙堆模型实验数据的数理统计分析如表3所示.实验统计结果显示,落沙量随PGA的增加，样本均值E(X)依次增加，变异系数Cν依次减小.

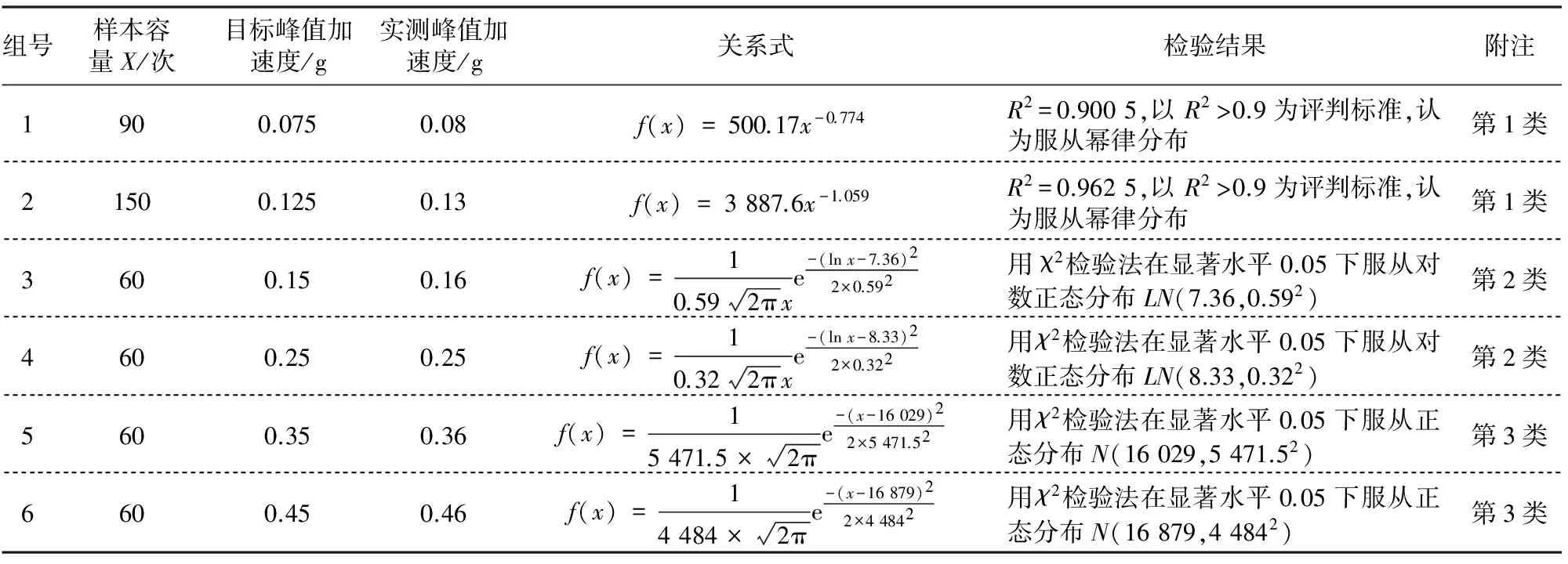
表2 假设检验统计表

注：PGA为0.075 g和0.125 g的两组实验落沙量会出现大量为0 g的情况，故实验次数有所增加，其他各组实验PGA不变，重复60次.

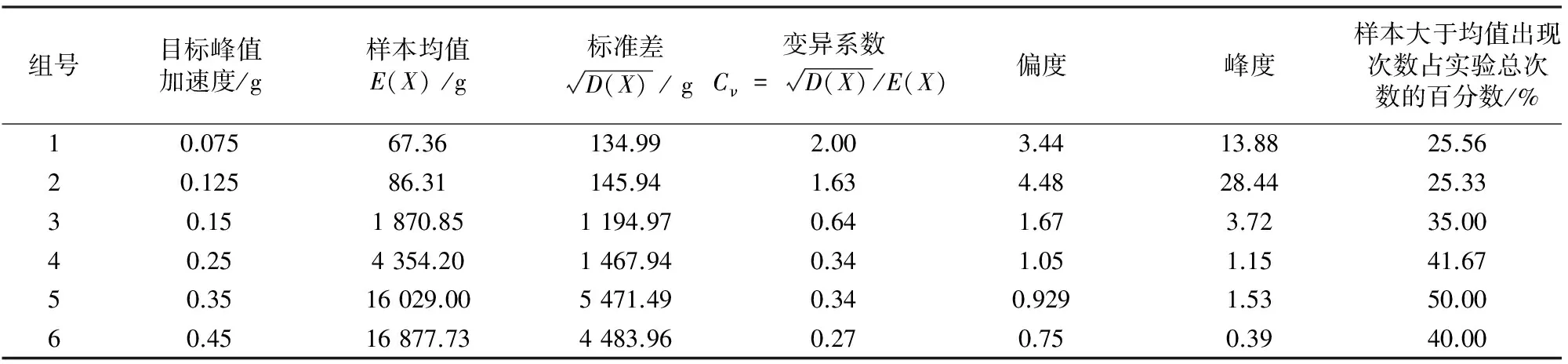
表3 实验结果统计表

2 地震波扰动下沙堆崩塌规模与频率关系的统计特性

由振动台沙堆模型实验数据统计特征结果发现，随地震波强度增加，统计崩塌规模与频率呈现3种概率分布，为进一步研究这3种概率分布转化的原因，需要了解3种概率分布的性质以及它们之间的区别与联系.

1)幂律分布性质.若非负的随机变量X服从幂律分布，则其概率密度f(x)可以表示为：

f(x)=cx-α.

(1)

式中：常数c>0；幂次α>0.对幂率分布概率公式(1)取对数后，lnf(x)和ln(x)之间呈直线关系，这一线性关系是判断给定的实例中随机变量是否满足幂律分布的依据.

幂律分布的共性是绝大多数事件发生的规模很小，而只有少数事件发生的规模相当大.在统计物理学领域中把幂律分布现象称为无标度现象，表明对于所观察的事件而言没有一个特征尺度，不同规模的事件均可以出现，并且小事件与大事件发生遵从同一诱发机制[12].

2)对数正态分布性质.如果随机变量X的函数Y=lnX服从正态分布N(μ′,σ′2)，则称X服从参数为μ′和σ′2的对数正态分布，简记X∽ln(μ′,σ′2).由正态分布的概率密度可推导出对数正态分布的概率密度f′(x).

(2)

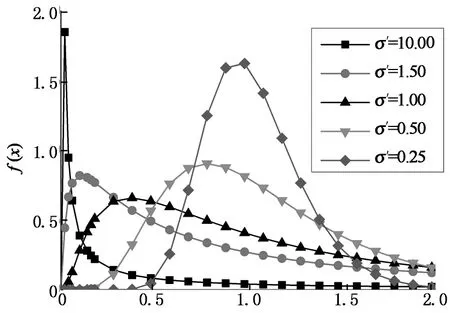
由式(2)可知，对数正态分布的概率密度中包含μ′，σ′2个参数，其中μ′值变化只会影响概率密度曲线的均值及峰值，σ′值的变化会导致概率密度曲线趋势发生转变[13].为此，将μ′值设定为某一定值，观察随σ′值的变化，概率密度曲线的演变趋势(图3和图4).

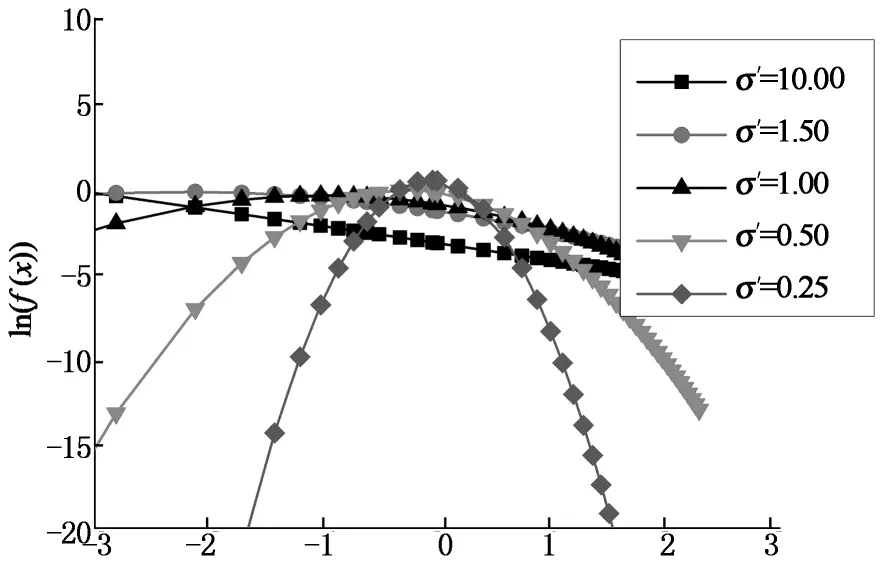
易见，在μ′值为定值时，对数正态分布的概率密度曲线随着σ′值增加逐渐接近幂律分布曲线(如图3中σ′=10时).当σ′=10时，对数正态分布的概率密度曲线取对数后已经近似成为一条直线(图4)；反之，随σ′值减小，对数正态分布概率密度曲线的偏度越来越小，从左偏曲线逐渐过渡到接近对称的钟形曲线(如图3中σ′=0.25时)，取对数后的二次抛物线，开口也逐渐减小(如图4中σ′=0.25时).

x

ln(x)

3)正态分布性质.若随机变量X具有的概率密度函数为：

(3)

则称X服从一个参数为μ，σ的正态分布，记为X∽N(μ,σ2).正态分布的概率密度函数曲线呈钟形曲线形势.

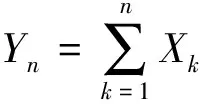
综上，幂律分布、对数正态分布、正态分布这3种概率分布之间存在着联系，其趋势变化与σ′值有关.当σ′值从大到小变化时，会导致概率密度从幂律分布-对数正态分布-正态分布的趋势转变[13,15].

更进一步，对影响σ′值的因素进行分析.根据矩估计法原理[13,16]，推导出σ′值的计算公式(4)，并将其表示成图5所示，由图5可见，σ′值是关于变量Cν的单调递增函数.因此，概率密度从幂律分布-对数正态分布-正态分布的趋势转变也可以用变异系数Cν的变化所反映，并且变异系数Cν是表征不同均值实验数据离散程度的指标[17]，具有明确的概念，可为以下具体现象的讨论提供更为直观的参数.

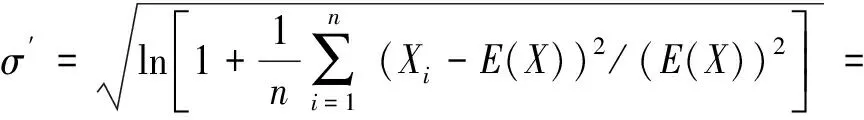
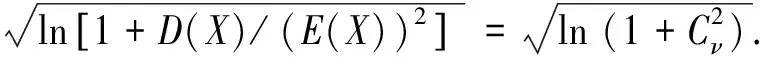
(4)

式中：σ′值为对数正态分布的参数；E(X)为样本均值；D(X)为样本方差；Xi为样本值.

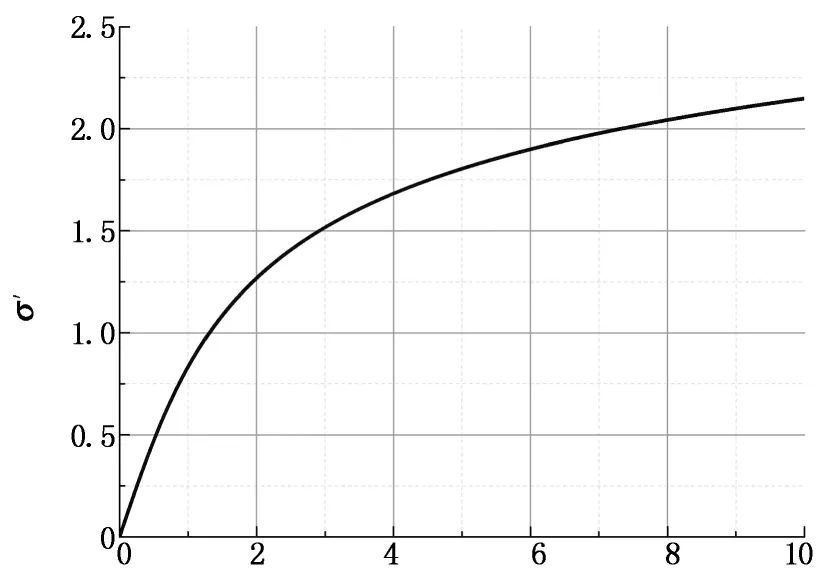
Cν

3 地震波强度递增沙堆模型统计特性转变的机理

1)通过近景摄影测量技术对沙堆模型坡体失稳过程进行监测，发现其行为随扰动递增呈现3种不同现象.

Ⅰ)沙堆表面颗粒在第1，2组实验(PGA=0.075～0.125g)的加速度峰值点出现点源启动事件(表4).所谓点源启动是指一处或几处分散在坡面的孤立颗粒失稳启动(图6(a)).点源启动后的颗粒在运动中可能会出现3种现象：①无沙粒滑出边界，整个坡面上的大部分颗粒处于静止状态，虽有少数颗粒发生滚动但未滚落出边界.②小规模沙粒滑出边界.处在坡面上部的颗粒启动时容易被下部的大颗粒阻挡，滑出边界的几率小；位于下部的颗粒滑出边界的几率大，但行程短，缺乏带动效应，即使发生连锁反应规模也有限.③大规模雪崩.坡面上少数颗粒先启动，并带动其他颗粒，迅速扩大规模，使一定范围内的颗粒发生失稳，最终演变成一次大规模的雪崩.其他时段，无颗粒启动现象.

Ⅱ)沙堆表面颗粒在第3，4组实验中(PGA=0.15～0.25g)的加速度峰值点同时发生点源启动和局部面源启动事件(表4).所谓局部面源启动是指集聚在一块区域内的颗粒瞬间启动(图6(b)).受扰动强度的影响，局部面源启动的颗粒在启动时获得了较大的初速度，使得其滚落出沙堆的几率增加，如在第3，4组实验中的落沙量已经没有出现落沙量为0的情况.其他时段，也有少量点源启动的事件发生.

Ⅲ)沙堆在第5，6组实验中(PGA=0.35～0.45g)的首个加速度峰值时段内发生面源启动事件(表4).即相对局部面源启动而言，规模扩大到整个坡面，使得大规模雪崩几乎成为必然事件，每次实验中由面源启动方式产生的落沙量占该次实验总落沙量的大部分；其他时段，点源启动的事件也屡有发生，但一般其落沙量仅占总量的小部分.

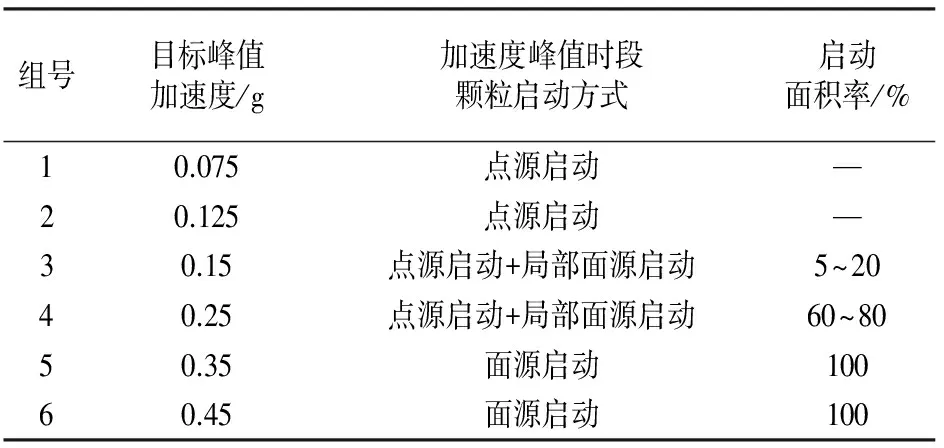
表4 加速度峰值时段颗粒启动方式

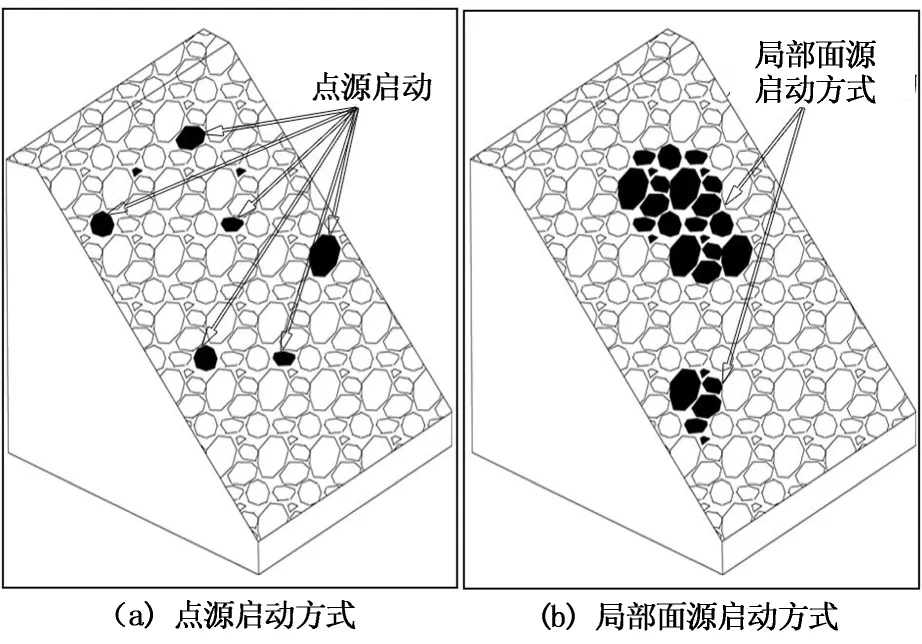
图6 颗粒启动方式

2)如上3种不同现象反映了3种不同类型的物理机制，并且通过分析3种物理机制的变化得知，颗粒失稳由相互作用占主导地位向振动驱动下各自独立下落的转化是造成落沙量的离散性(Cν)减小的原因.

a)自组织状态模式(PGA=0.075～0.125g)：在点源启动的情况下，沙堆表面颗粒失稳以相互作用为主.加速度峰值点产生点源启动现象，点源启动后的颗粒会对相邻颗粒产生扰动并通过近邻的相互作用发生连锁反应.相互作用主要体现为以下3种方式：①滚动的颗粒撞击下部颗粒；②启动的颗粒减小了上方颗粒的支撑力；③启动的颗粒对两侧颗粒产生侧向摩擦.但邻近颗粒在受到由连锁反应传递的扰动时不至于总是超过其自稳能力，会面临扰动停止(即活动性消失)或者扰动继续传播(即活动性分叉)的选择.因此这种连锁反应造成落沙量之间的差距极大，呈现出很大的离散性(Cν)与不确定性.例如以PGA为0.125g为例，最小落沙量为0，最大落沙量为1.252kg，最大落沙量与最小落沙量比值趋于无穷大.

b)振动力控制模式(PGA=0.35～0.45g)：在面源启动的情况下，沙堆表面颗粒失稳以各自独立下落为主.发生面源启动的颗粒是由振动力直接触发而启动的，其启动方式相互独立，无需依赖邻近颗粒的带动就具有一定的初速度，多数能滑落出沙堆，大规模雪崩几乎成为必然事件，成为总落沙量的主体，故离散程度(Cν)小.例如以PGA=0.45g为例，最小落沙量为8.995kg，最大落沙量为29.666kg，最大落沙量与最小落沙量比值约为3.3.面源启动颗粒失稳的机理以颗粒独立启动为主，由中心极限定理的定义可知，这就是其总体效应(落沙量)服从正态分布的原理.

c)过渡模式(PGA=0.15～0.25g)：同时发生点源启动和局部面源启动表明沙堆表面颗粒受到自组织状态模式和振动力控制模式的相互影响.随扰动递增，颗粒失稳由相互作用占主导地位向振动驱动下各自独立下落逐渐转化，故落沙量的离散性(Cν)逐渐减小.例如以PGA=0.15g为例，最小落沙量为0.485kg，最大落沙量为6.730kg，最大落沙量与最小落沙量比值约为13.9.

综上，在微扰动情况下，颗粒失稳以相互作用为主，崩塌滑坡的动力学特性受制于系统的SOC作用，系统的不确定性、离散程度最大；当扰动强度进一步增加时，斜坡系统受振动力影响增强，系统的不确定性、离散程度进一步减小，崩滑规模与发生频率的幂律式逐渐弱化，发展为具有对数正态分布的曲线特征；当扰动强度继续增加，使得颗粒失稳以各自独立下落为主时，崩塌滑坡的表观响应趋于完全被振动力所控制，系统的不确定性、离散程度最小，发展为具有正态分布的曲线特征.

4 对汶川地震触发崩塌滑坡分布规律的解释

利用2008年6月4日的一套ALOS卫星图像(精度达10m)资料，对汶川地震Ⅹ,Ⅺ度区的崩塌滑坡的面积进行人工解译.受资料精度要求统一的限制，选取了北川、安县、茂县和绵竹境内(坐标范围为103°57′36″E～104°36′36″E，31°30′N～31°58′48″N，面积约672km2)及都江堰、彭州境内(坐标范围为103°37′12″E～103°45′36″E，31°12′36″N～31°21′36″N，面积约445平方公里)的两片区域.通过统计分析得到了汶川地震Ⅹ度,Ⅺ度地震烈度区崩滑面积与累计频率的统计关系，如表5所示.在Ⅹ度区，判译出了崩塌滑坡2 812处，崩塌滑坡面积与累计频率呈现幂律分布，其变异系数Cν为5.1；在Ⅺ度区，判译出了崩塌滑坡3 159处，崩塌滑坡面积与累计频率呈现对数正态分布，其变异系数Cν为1.8.

沙堆模型与实震诱发崩塌滑坡等原型问题具有一定的相似性，基于上节对沙堆模型统计特性的分析，揭示了地震强度递增，会造成沙堆模型变异系数Cν的减小，并使落沙量与累计频率的概率分布发生转变的规律.该结论在汶川实震资料的整体分布规律的分析中也同样适用.因此，根据物理普适性原理，汶川地震实震资料的规律可能是具普适性意义的现象.

表5 汶川地震Ⅹ度,Ⅺ度烈度区崩塌滑坡面积与累计频率统计关系[18]

注：N为滑坡数量，A为滑坡面积.

5 结 论

1)在自组织临界理论下，开展了振动台沙堆模型实验，发现随地震扰动强度增加，落沙量与累计频率会遵循从幂律分布-对数正态分布-正态分布3种概型的依次转变，其转变机理与变异系数Cν有关，Cν从大到小变化时，会导致概率密度从幂律分布-对数正态分布-正态分布的趋势转变.振动台实验数据与汶川实震数据共同验证了在地震烈度单一因素递增情况下，变异系数Cν逐渐减小，地震触发的崩塌滑坡分布规律遵循从幂律分布-对数正态分布.该认识具有一定的普适性，可以为高烈度地震山区地震触发崩塌滑坡灾势预测提供具有物理理论依据的概型，从而为开展地震触发山地灾害危险性区划、地震次生灾害风险评估等工作提供科学依据.

2)在对SOC系统的研究中，扰动因素是一直被忽视的.国内外各类有关SOC系统的研究多是在微扰动的情况下完成的[2,5,19-20]，而对其在变扰动情况下的性质如何变化却鲜有研究，但在实际的自然界中，有关变扰动的自然现象却是十分常见的，如灾变事件的扰动强度变化范围可能会达到几个数量级.据此，首次开展了不同扰动强度下(不同峰值加速度)的振动台沙堆模型实验，并得知颗粒失稳由相互作用占主导地位向振动驱动下各自独立下落的转化是导致Cν减小的物理机制，这种物理机制的变化是造成沙堆模型统计特性转变的原因.该研究拓展了SOC传统的灾变理论的研究领域.

[1]BAKP,CHENK.Self-organizedcriticality[J].ScientificAmerican,UnitedStates, 1991, 264(1): 26-33.

[2]HELDGA,SOLINASDH.Experimentalstudyofcritical-massfluctuationsinanevolvingsand-pile[J].PhysicalReviewLetters, 1990, 65(9): 1120-1123.

[3] 姚令侃，黄渊，陆阳.自组织临界性及其在斜坡重力作用灾害研究中的应用[J]. 中国科学(E辑),2003, 33(S1): 17-27.

YAOLin-kan,HUANGYuan,LUYang．Self-organizedcriticalityanditsapplicationintheslopedisastersundergravity[J].ScienceinChina(SeriesE),2003,33(S1):17-27.(InChinese)

[4]YAOLK,QIY.FractalcharacteristicsofgravitylandformanditsSOCmechanism[J].WuhanUniversityJournalofNaturalSciences,2007,12(4):605-609.

[5] 姚令侃, 李仕雄, 蒋良潍. 自组织临界性及其在散粒体研究中的应用[J]. 四川大学学报:工程科学版, 2003, 35(1): 8-14.

YAOLin-kan,LIShi-xiong,JIANGLiang-wei.Self-organizedcriticalityanditsapplicationingranularmixtures[J].JournalofSichuanUniversity:EngineeringScienceEdition, 2003, 35(1): 8-14. (InChinese)

[6]FUYIIY.Frequencydistributionofthemagnitudeoflandslidescausedbyheavyrainfall[J].JournaloftheSeismologicalSocietyofJapan, 1969, 22(1): 244-247.

[7]HOVIUSN,STARKCP,ALLENPA.Sedimentfluxfromamountainbeltderivedbylandslidemapping[J].Geology, 1997, 25(3): 231-234.

[8]HOVIUSN,STARKCP,HAO-TSUC,etal. Supply and removal of sediment in a landslide-dominated mountain belt: Central Range, Taiwan[J]. The Journal of Geology, 2000, 108(1): 73-89.

[9] YAO L K, QI Y. Fractal characteristics of gravity landform and its SOC mechanism[J]. Wuhan University Journal of Natural Sciences, 2007, 12(4): 605-609.

[10]姚令侃,黄艺丹,杨庆华. 地震触发崩塌滑坡自组织临界性研究 [J].四川大学学报:工程科学版,2010,42(5):33-43.

YAO Lin-kan,HUANG Yi-dan, YANG Qing-hua. The self-organized criticality of landslids triggered by earthquake[J].Journal of Sichuan University:Engineering Science Edition,2010,42(5):33-43. (In Chinese)

[11]杨庆华,姚令侃,齐颖,等.散粒体离心模型自组织临界性及地震效应分析[J].岩土工程学报，2007,29(11)：1630-1635.

YANG Qing-hua, YAO Lin-kan, QI Ying,etal. Analysis of self-organized criticality of centrifugal model tests on granular mixtures and earthquake effect [J]. Chinese Journal of Geotechnical Engineering,2007, 29(11): 1630-1635. (In Chinese)

[12]胡海波,王林.幂律分布研究简史[J].物理,2005,34(12):889-896.

HU Hai-bo, WANG Lin. A brief history of power law distributions[J]. Physics, 2005,34(12): 889-896. (In Chinese)

[13]LIMPERT E, STAHEL W A, ABBT M. Log-normal distributions across the sciences: keys and clues [J]. BioScience, 2001, 51(5): 341-352.

[14]李裕奇,赵联文,王沁,等.概率论与数理统计[M].北京:国防工业出版社,2011:193-198.

LI Yu-qi, ZHAO Lian-wen, WANG Qin,etal.The theory of probability and statistics [M].Beijing: National Defense Industry Press, 2011:193-198.(In Chinese)

[15]於崇文．地质系统复杂性[M].北京:地质出版社,2003,12:1019-1095.

YU Chong-wen. Complexity of geosystem [M].Beijing: Geological Publishing House, 2003:1019-1095. (In Chinese)

[16]于洋.对数正态分布的几个性质及其参数估计[J].廊坊师范学院学报:自然科学版,2011,11(5)：8-11.

YU Yang.Several properties of the lognormal distribution and estimation of its parameters[J].Journal of Langfang Teachers College:Natural Science Edition, 2011,11(5):8-11. (In Chinese)

[17]贾俊平,何晓群,金勇进.统计学[M].北京:中国人民大学出版社,2006:102-104.

JIA Jun-ping, HE Xiao-qun, JIN Yong-jin. Statistics[M]. Beijing: China Renmin University Press,2006:102-104. (In Chinese)

[18]黄艺丹,姚令侃,郭沉稳. 基于元胞自动机的地震触发崩塌滑坡分布规律[J].西南交通大学学报,2013,48(4):609-615.

HUANG Yi-dan, YAO Lin-kan, GUO Chen-wen. Distribution law of landslides triggered by earthquake based on cellular automata[J].Journal of Southwest Jiaotong University,2013, 48(4):609-615. (In Chinese)

[19]FRETTE V, ETAL K C. Avalanche dynamics in a pile of rice [J]. Nature, 1996, 379(27): 49-52.

[20]BRETZ M, JEVNE B E. Imaging of avalanches in granular materials [J]. Physical Review Letters, 1992, 69(16): 2431-2434.

Study on the Response Mechanism of Sandpile Model Tests with Increased Seismic Loading

GUO Hai-qiang1, YAO Ling-kan1,2,3†,GUO Chen-wen1,HUANG Yi-dan1

(1.School of Civil Engineering, Southwest Jiaotong Univ, Chengdu,Sichuan 610031,China; 2.MOE Key Lab of High-Speed Railway Engineering,Chengdu, Sichuan 610031,China; 3. Road and Railway Engineering Research Inst, Sichuan Key Lab of Aseismic Engineering and Technol, Chengdu, Sichuan 610031,China )

According to the phenomenon of statistical relationships showing different distributions, between the area and cumulative frequency of landslides in Ⅹ,Ⅺ seismic intensity of Ms 8.0 Wenchuan earthquake, 6 sandpile model tests under seismic were conducted with the increase of seismic peak ground acceleration ranging from 0.075 g to 0.450 g. The phenomenon of statistical relationships was reproduced by the tests between the amount and cumulative frequency of sand changing from power-law distribution to lognormal distribution, then to normal distribution, with increase of seismic loading. By mathematical analysis, the decrease of the coefficient of variation is the cause of probability distribution shift between power-law, lognormal distribution and normal distribution. Observed through experiments, the performance of grains on the surface of sandpile will show different models with the increase of seismic loading. Under weak vibration, the probability that the activity will die is overall balanced with the probability that the activity will branch. A large-scale collapse occurs when there is a chain interaction between neighboring grains. It has the greatest uncertainty. Under strong vibration, most grains start independently. A large-scale collapse becomes a certain event. Therefore, the scale of collapse is transformed from the chain reaction of unstable grains triggered by self-organized effect to the independent falling of unstable grains triggered by vibrating force effect, which is the physical mechanism of the reducing ofCv. According to the above realization, the phenomenon of the relation between area and cumulative frequency changing from power-law distribution to lognormal distribution with the increase of seismic intensity of Ms 8.0 Wenchuan earthquake may be universal.

earthquake；landslide；self-organized criticality(SOC)；sandpile model test；coefficient of variation

1674-2974(2015)05-0099-08

2014-06-26

国家自然科学基金资助项目(41172321)，National Natural Science Foundation of China(41172321)；国家自然科学基金重点资助项目(41030742), Major Research Project of National Natural Science Foundation of China (41030742)；铁道部科技研究开发计划课题(2011G019-B)

郭海强(1987-)，男，吉林桦甸人，西南交通大学博士研究生

†通讯联系人，E-mail: yaolk@swjtu.edu.cn

TU435;P694

A