钢筋混凝土剪扭构件承载力计算公式的研究*

张望喜，韩 江

(湖南大学 土木工程学院, 湖南 长沙 410082)

钢筋混凝土剪扭构件承载力计算公式的研究*

张望喜†，韩 江

(湖南大学 土木工程学院, 湖南 长沙 410082)

《混凝土结构设计规范》(GB 50010-2010)(以下简称《规范》)在剪扭复合作用构件承载力计算中采用三段折线关系，将1/4圆弧外扩，导致设计偏于危险；丁大钧建议公式使用1/4圆弧模型，但在选取混凝土剪力项折减系数时低估了混凝土部分的抗剪能力；黄靓建议公式使用内缩的直线模型，设计偏于保守.在1/4圆弧相关关系的基础上提出两种修正公式.实例对比表明，两种修正公式安全于《规范》公式.算例分析表明，两种修正公式既能完全满足1/4圆弧相关关系，又较好地满足了黄靓提出的直线相关关系且两种修正公式计算结果相当接近.

钢筋混凝土；剪扭构件；承载力计算；修正公式

在钢筋混凝土结构中，受纯扭的构件比较少见，大都伴有弯、剪存在[1]，前人对纯剪[2-3]、弯扭相关性[4]进行了大量的研究．因而研究有腹筋构件的剪扭相关性对于保证构件设计安全、合理具有重要意义.

廉晓飞等人[5-6]对14根无腹筋和有腹筋钢筋混凝土矩形梁进行剪扭试验，研究表明无腹筋梁剪扭承载力较好地符合1/4圆弧相关关系.有腹筋梁剪扭承载力同样符合1/4圆弧的相关关系.钢筋混凝土结构抗扭专题组[7]研究表明剪扭共同作用时，强度有明显的降低趋势，可按1/4圆弧相关曲线处理.丁大钧[8]按照1/4圆弧曲线不作任何简化提出一种修正公式，并指出公式在计算时没有增加多少工作量且上下限自动满足.康谷贻、王士琴[9]研究表明受剪扭共同作用构件的强度关系曲线主要影响因素为剪跨比λ和顶部纵筋与底部纵筋强度比r.在λ=0且r接近1时，几乎为一直线，并给出不同λ和r情况下剪扭相关关系图，如图1.黄靓等人[10-11]对1/4圆弧相关关系简化为直线模型并通过计算指出：《混凝土结构设计规范》(GB 50010-2002)在计算钢筋混凝土剪扭构件承载力时采用“三折线”模型使混凝土部分提供的承载力被放大，导致设计偏于危险并在直线模型的基础上提出2种修正公式，并进行了可靠度研究.

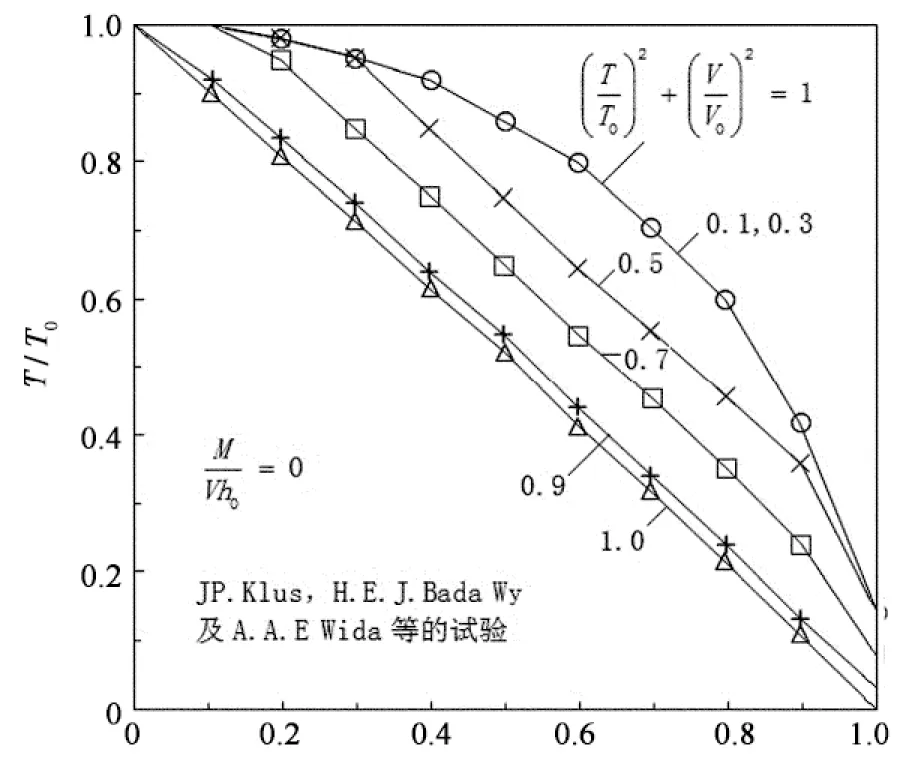
V/V0(a)剪跨比λ=0

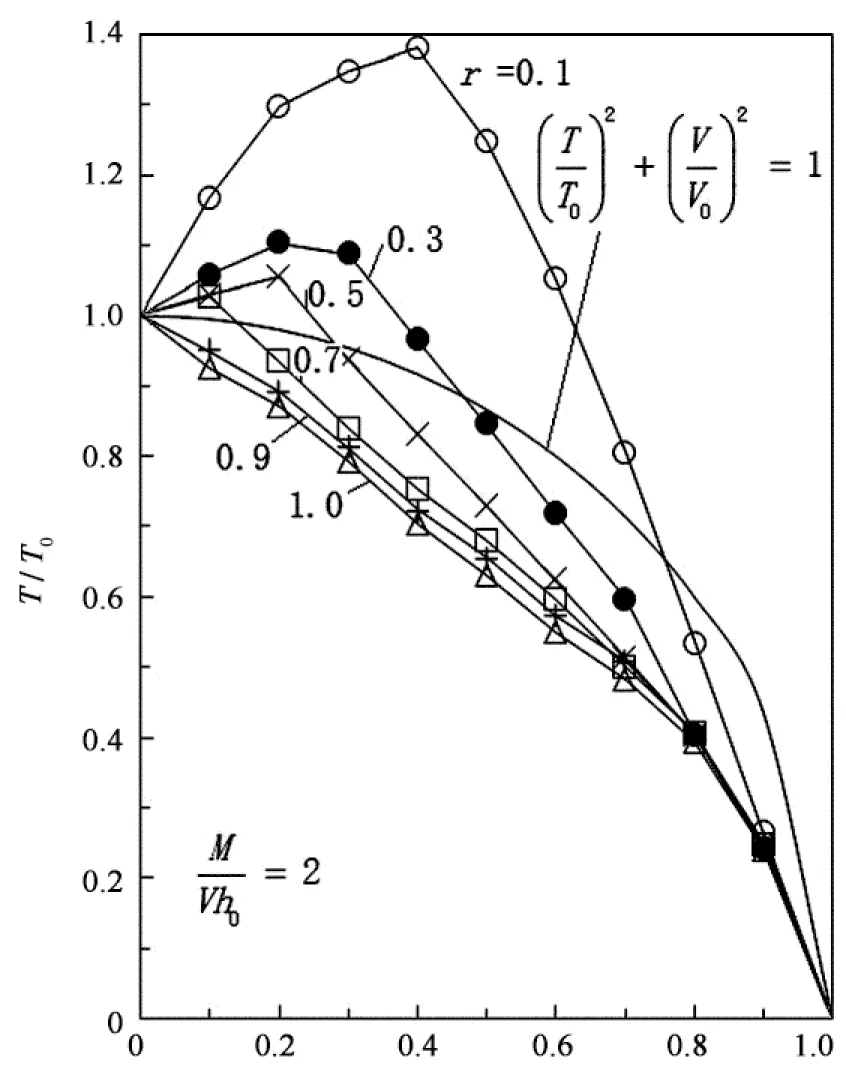
V/V0(b)剪跨比λ=2

V/V0(c)剪跨比λ=3

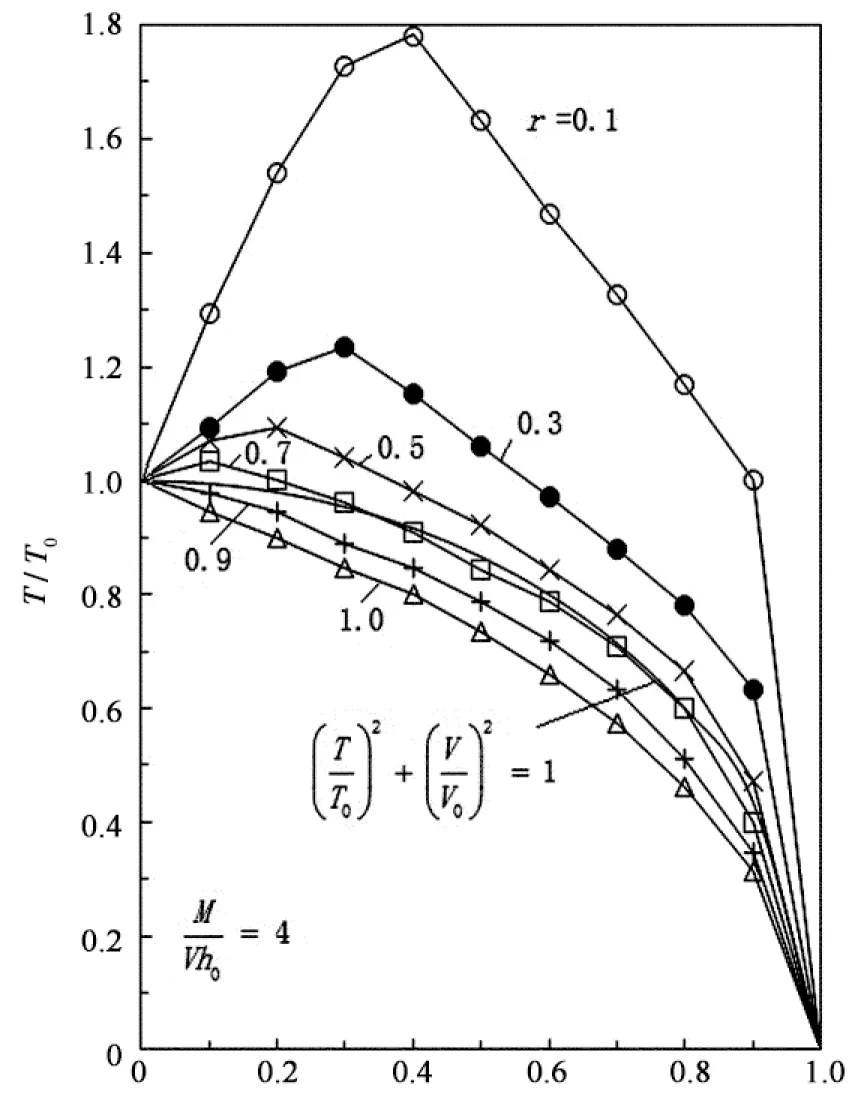
V/V0(d)剪跨比λ=4

1 《规范》、丁大钧和黄靓建议公式

我国《混凝土结构设计规范》(GB 50010-2010)[12](以下简称《规范》)在考虑混凝土部分剪扭承载力相关关系时，使用简化的3段折线关系代替1/4圆弧关系，如图2所示.其中Vc和Tc分别表示有腹筋构件混凝土部分提供的抗剪和抗扭承载力，Vc0和Tc0分别表示纯剪构件抗剪承载力公式中的混凝土项和纯扭构件抗扭承载力公式中的混凝土项.

Tc/Tc0

《规范》规定一般剪扭构件受剪承载力和受扭承载力如下：

(1)

(2)

式中βt为一般剪扭构件混凝土受扭承载力降低系数，按式(3)计算.当βt小于0.5时，取0.5；当βt大于1.0时，取1.0.

(3)

式中V为剪力设计值；T为扭矩设计值；ft为混凝土抗拉强度设计值；fyv为箍筋的抗拉强度设计值；Asv为抗剪所需的箍筋截面面积；Ast1为抗扭箍筋的单肢截面面积；Wt为截面抗扭塑性抵抗矩；ζ为受扭的纵向普通钢筋与箍筋的配筋强度比，用式(4)计算，ζ值不应小于0.6，当ζ大于1.7时，取1.7.

(4)

丁大钧建议使用1/4圆弧曲线模型不作任何修正，如图2所示，并指出Tc0按照βt折减，Vc0按照(1-βt)折减，因此对于一般剪扭构件其计算公式如下：

(5)

(6)

(7)

黄靓建议使用直线模型代替《规范》“三折线”模型，如图2所示，对于一般剪扭构件其计算公式如下：

(8)

(9)

(10)

本文基于现有试验结果认为混凝土部分剪扭相关关系符合1/4圆弧曲线，而《规范》采用的“三折线”模型将1/4圆弧曲线外扩，使混凝土部分提供的承载力被放大，设计偏于不安全.丁大钧公式使用1/4圆弧模型，但由后文算例可看出，公式(5)右边混凝土项的折减系数(1-βt)选取过于保守，导致计算配筋面积过大.黄靓公式使用1/4圆弧相关关系内缩的直线模型，相当于对所有剪扭构件的相关关系均取为内缩直线模型(Tc/Tc0+Vc/Vc0=1.0)，而由图1可看出：只有剪跨比接近于零且顶部与底部纵筋强度比接近于1时，其无量纲相关关系才近似于直线Tc/Tc0+Vc/Vc0=1.0，因此黄靓公式对于大多数构件的计算偏于保守.在此基础上，本文提出2种建议公式.

2 建议采用的修正公式一

修正公式一沿用丁大钧模型即1/4圆弧模型(如图2)，对《规范》公式进行修正：

以一般剪扭构件为例,由

(11)

将Tc0=0.35ftWt和Vc0=0.7ftbh0代入式(11)，得：

(12)

参照《规范》公式，用设计值之比V/T近似代替Vc/Tc，可得:

(13)

同理

(14)

令

(15)

(16)

不难看出：

(17)

则式(13),(14)简化为：

Tc=0.35βtftWt

(18)

(19)

得一般剪扭构件剪扭承载力公式如下：

(20)

(21)

式中βt按式(15)计算.

对于集中荷载作用下的独立剪扭构件，其承载力计算公式如下：

(22)

(23)

式中系数βt按下式计算：

(24)

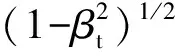
3 建议采用的修正公式二

《规范》使用图2所示 “三折线”关系代替1/4圆弧关系：当Tc/Tc0≤0.5时，忽略扭矩影响，取Vc/Vc0=1；当Vc/Vc0≤0.5时，忽略剪力影响，取Tc/Tc0=1.笔者认为此近似关系并不合适，当Tc/Tc0=0.5时，按照1/4圆弧关系计算Vc/Vc0=0.866，若仍取Vc/Vc0=1计算，混凝土部分所提供承载力则被高估13.4%，使设计偏于危险.在此分析基础上，修正公式二使用修正的“三折线”模型近似代替1/4圆弧关系，如图3.当Tc/Tc0=0.3时，按1/4圆弧关系计算Vc/Vc0=0.954，混凝土部分的承载力被高估4.6%，远小于《规范》“三折线”模型的13.4%，因此可认为修正公式二模型可近似代替1/4圆弧的相关关系.

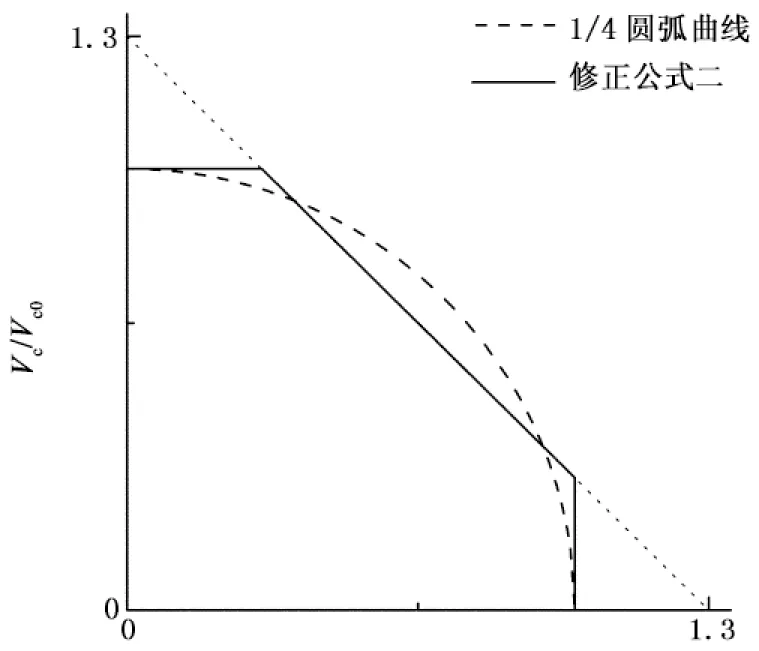
T/Tc0

修正公式二推导如下：

1)当Tc/Tc0≤0.3时，取Vc/Vc0=1；

2)当Vc/Vc0≤0.3时，取Tc/Tc0=1；

3)当0.3≤Tc/Tc0≤1.0时，用直线Tc/Tc0+Vc/Vc0=1.3代替圆弧相关，可得

(25)

参照《规范》公式，用设计值之比V/T近似代替Vc/Tc，有:

(26)

根据图3，有0.3≤βt≤1.0．

由此得一般钢筋混凝土剪扭构件剪扭承载力公式如下：

(27)

(28)

对于集中荷载作用下的独立剪扭构件，其承载力计算公式如下：

(29)

(30)

(31)

修正公式二同样利用 “三折线”模型代替1/4圆弧模型，与《规范》公式相似，易于工程人员理解和应用.虽看似有部分区域外扩，但相比《规范》公式，修正公式二有效控制了《规范》模型的外扩.后文的实例对比和算例计算表明，修正公式二使用的“三折线”模型外扩区域并未使得计算偏于危险，计算结果与修正公式一相当接近且明显安全于《规范》公式.

4 实例对比

下面使用《规范》公式、修正公式一和二与文献[6]所做的11根钢筋混凝土矩形截面有腹筋梁的试验作对比.试验参数如表1.试验值与3种公式计算值见表2.

文献[13]指出，承载能力储备指标反映了结构构件承受超载的能力，其计算公式为:

(32)

式中Fu,Fd分别为结构构件达到极限点和设计点时的承载能力.

表2中V*,T*为试验所得有腹筋梁极限承载能力，3种公式计算的V0，T0值为对应公式的设计承载能力，因此各公式计算的V*/V0即为承载能力储备指标KF，KF值越大则安全储备越高.由表2看出，对同一试件修正公式一、二的V*/V0值均大于《规范》公式的V*/V0值.由此可见，修正公式一、二承载能力储备高于《规范》公式.

表1 试件参数

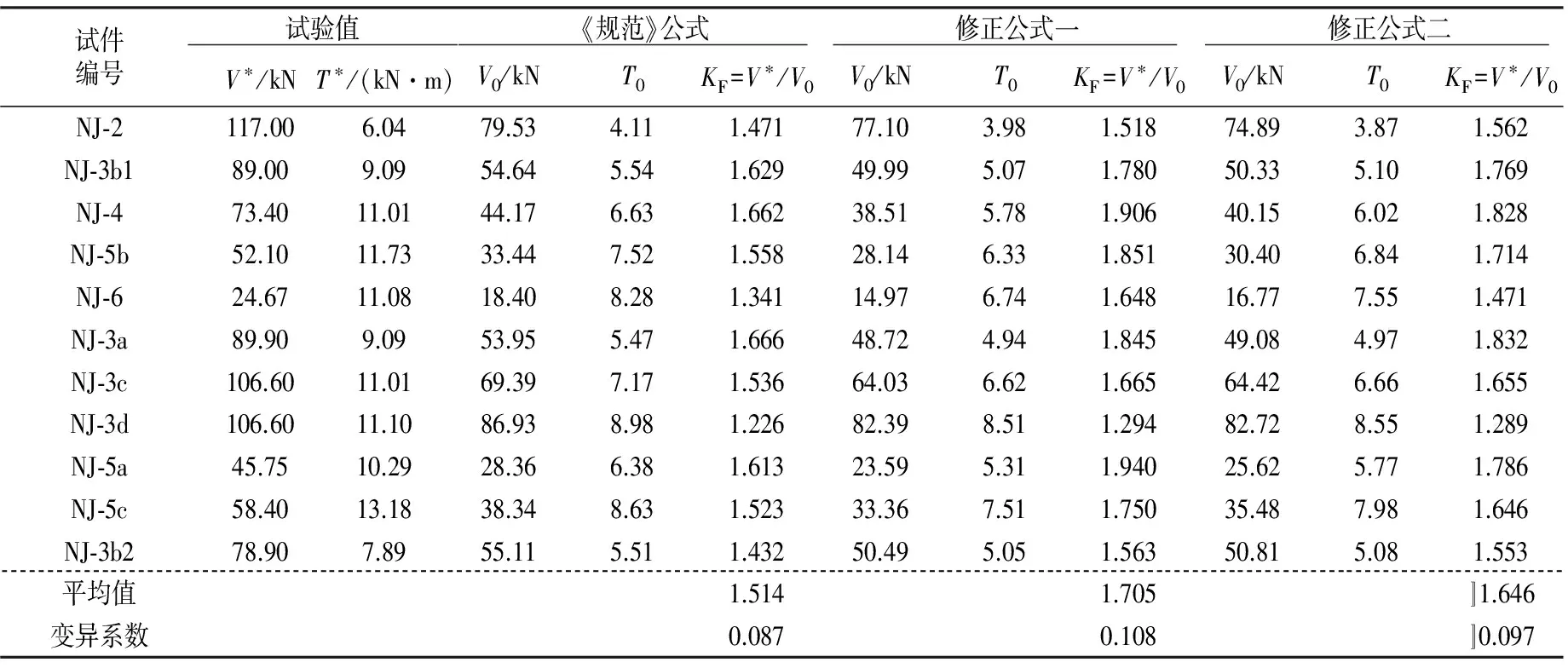
表2 试验值与3种公式计算值

5 算例分析

下面通过一般荷载作用下的矩形截面钢筋混凝土梁为例(箍筋采用HPB300级钢筋，双肢箍，ζ取1.3)，来比较修正公式一、二和《规范》公式、丁大钧公式及黄靓公式的安全性.

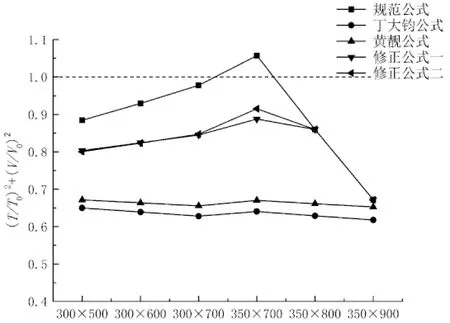
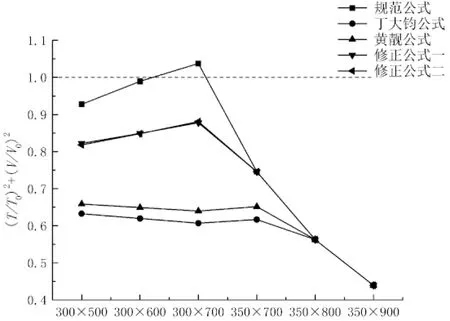
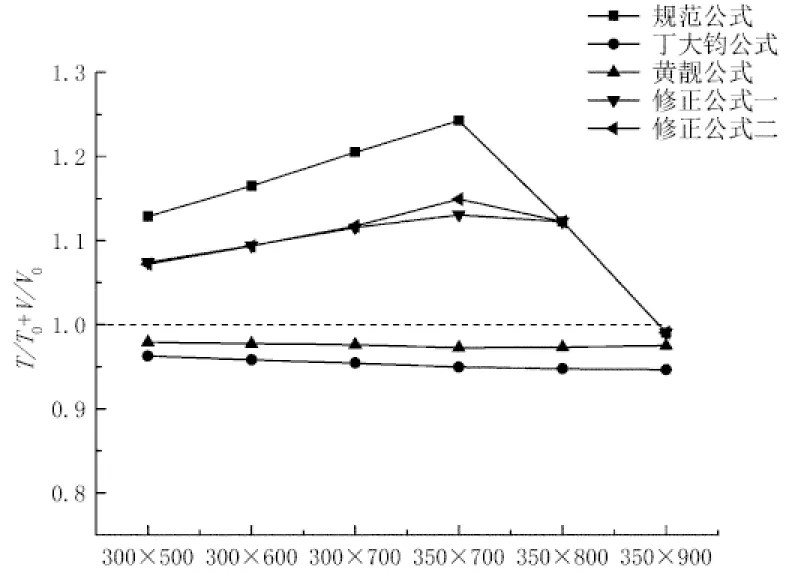
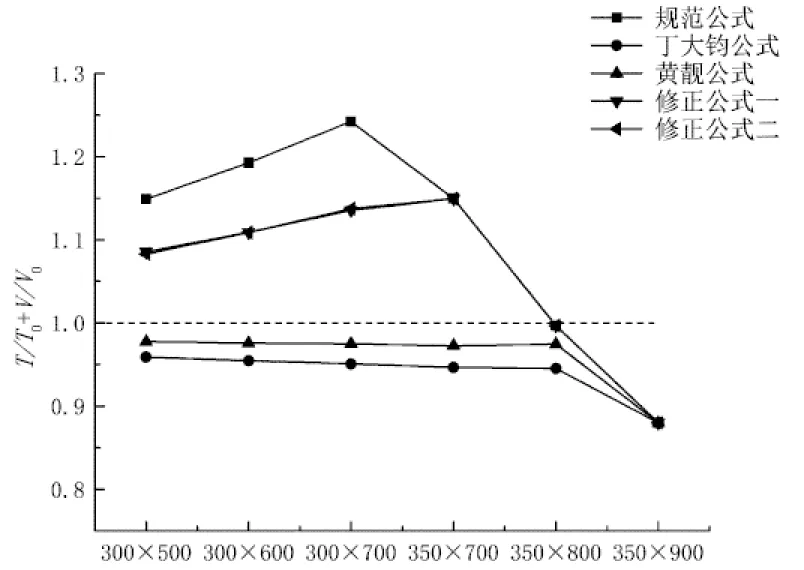
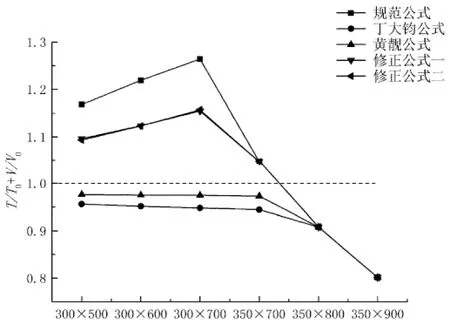
本文在经过大量计算并考虑最小配筋率的情况下，以设计值T=8 kN·m，V=300 kN、混凝土强度等级C25～C35为例，验算5种公式的 (T/T0)2+(V/V0)2和T/T0+V/V0，结果如图4和图5所示.

(b×h)/(mm×mm)(a)C25

(b×h)/(mm×mm)(b)C30

(b×h)/(mm×mm)(c)C35

(b×h)/(mm×mm)(a)C25

(b×h)/(mm×mm)(b)C30

(b×h)/(mm×mm)(c)C35

由图4可看出，用1/4圆弧模型验算，《规范》公式计算的(T/T0)2+(V/V0)2随着梁尺寸增大先有增大趋势，随后由于最小配筋率的限制， (T/T0)2+(V/V0)2急剧减小，在最大值处，《规范》公式不能满足1/4圆弧模型即(T/T0)2+(V/V0)2>1.丁大钧公式计算的(T/T0)2+(V/V0)2基本分布在0.7以下，随着梁尺寸增大其变化幅度较小，此算例可以看出，丁大钧公式选取较为保守的剪力折减系数，导致计算配筋面积增加.黄靓曲线和丁大钧曲线相似，这与黄靓选取直线相关模型使得配箍率增加有关.本文提出的两种修正公式计算结果相当接近，(T/T0)2+(V/V0)2随梁尺寸的变化规律基本与《规范》公式相似，两修正公式最大值分别为0.899和0.920，相比《规范》公式是偏于安全的.

图5可看出，用黄靓提出的直线模型验算，《规范》公式计算的(T/T0+V/V0)在梁尺寸较小时均在1.1以上，最大值达到1.246，对比图1可知，在剪跨比λ和顶部纵筋与底部纵筋强度比r较大的情况下，《规范》公式并不合理.本文提出的两种修正公式计算的(T/T0+V/V0)值在1.1附近，最大值分别为1.155和1.157，很大程度上提高了《规范》公式的安全性.由图1可看出，除了λ=0且r=0.8～1.0以外，相关关系基本满足T/T0+V/V0>1.1，因此修正公式计算结果仍能保证安全，但在λ=0，r=0.8～1.0时，两种修正公式尚不能确保安全.用丁大钧和黄靓公式计算的(T/T0+V/V0)值均小于1，计算偏于保守.

通过更多算例可发现，用1/4圆弧相关关系验算《规范》公式，出现(T/T0)2+(V/V0)2>1并非偶然，如图6(T=5 kN·m，V=250 kN).

(b×h)/(mm×mm)

由图6可看出，混凝土强度等级为C20～C25，截面尺寸为300 mm×500 mm～300 mm×700 mm时，用《规范》公式计算的(T/T0)2+(V/V0)2均大于1，说明《规范》采用三段折线关系将1/4圆弧外扩，导致设计偏于危险.用其它4种公式验算，均有(T/T0)2+(V/V0)2<1，表明4种公式修正效果较为理想.

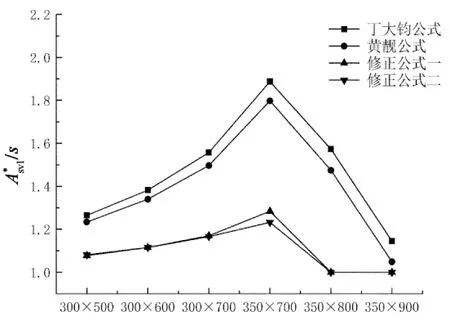
由图7给出了考虑最小配筋率情况下，T=8 kN·m，V=300 kN，混凝土强度C25～C35，丁大钧公式、黄靓公式、修正公式一、修正公式二与《规范》公式计算所需Asv1*/s之比.

由图7可看出，丁大钧和黄靓公式与《规范》公式所需Asv1*/s之比均较高，丁大钧公式最高达到2.033，黄靓公式最高达到1.919.修正公式一和二计算结果相当接近,最高值分别为1.291和1.284.

(b×h)/(mm×mm)(a)C25

(b×h)/(mm×mm)(b)C30

(b×h)/(mm×mm)(c)C35

综合图4～图7，从安全性看，丁大钧公式(T/T0)2+(V/V0)2和T/T0+V/V0计算值均小于1.0，在5个公式中最为安全可靠，黄靓公式也较为安全.但从经济性看，丁大钧和黄靓公式与《规范》公式所需Asv1*/s之比最高值分别为2.033和1.919，也就是说按照丁大钧、黄靓公式计算配筋需在《规范》公式Asv1*/s的基础上分别提高103.3%和91.9%，这在经济角度并不合理.两种修正公式在适当提高《规范》公式计算配箍率(最高29.1%)的基础上，既能很好地满足1/4圆弧相关关系，又较好地满足了黄靓提出的直线相关关系，安全性和经济性都较为合理.

由式(4)可得，当ζ一定，抗扭纵筋截面面积Astl与Ast1/s成正比，因此4种公式与《规范》公式所需Astl之比与图7相似.

6 结 论

1)《规范》公式在剪扭构件承载力计算时采用“三折线”相关关系，将1/4圆弧外扩，导致设计偏于危险.

2)丁大钧公式低估了混凝土部分的抗剪能力，选取较为保守的混凝土剪力项折减系数，导致计算抗剪箍筋面积大幅增加，安全储备较高但经济性较差.

3)黄靓将所有情况均按照1/4圆弧内缩的直线模型计算，计算偏于保守导致计算配筋大幅提高，安全储备较高但经济性较差.

4)本文提出的两种修正公式在适当提高《规范》公式计算配筋的基础上，既很好地满足1/4圆弧相关关系，又较好地满足黄靓提出的直线相关关系，安全性和经济性都较为合理，且两种修正公式计算结果相当接近.

5)本文建议钢筋混凝土剪扭构件承载力按照修正公式一或二计算，在剪跨比λ=0且顶部与底部纵筋强度比r=0.8～1.0时，适当提高配筋率或者按丁大钧公式或黄靓公式计算，如此便可同时保证设计的安全性和经济性.

[1] 沈蒲生, 梁兴文. 混凝土结构设计原理[M].北京:高等教育出版社，2007:160-180.

SHEN Pu-sheng, LIANG Xing-wen. The design theory for concrete structure[M]. Beijing: Higher Education Press, 2007:160-180. ( In Chinese)

[2] 郑辉, 方志, 曹敏辉. 配置竖向预应力钢筋混凝土箱梁抗剪性能试验[J].湖南大学学报：自然科学版, 2013, 40(1): 1-8.

ZHENG Hui, FANG Zhi, CAO Ming-hui. Experimental study on the shear behavior of reinforced thin-wall box girders with vertical prestressed tendon[J]. Journal of Hunan University：Natural Sciences, 2013, 40(1): 1-8. (In Chinese)

[3] 何益斌, 李毅, 曹海信, 等. T形钢连接梁柱节点的试验和抗剪计算方法研究[J].湖南大学学报：自然科学版, 2012, 39(11): 1-6.

HE Yi-bin, LI Yi, CAO Hai-xin,etal. Experimental research on and calculation method for the shear strength of composite column-to-beam connections through T-stubs[J]. Journal of Hunan University：Natural Sciences, 2012, 39(11): 1-6. (In Chinese)

[4] 张望喜, 易伟建. 钢筋混凝土弯扭构件承载力验算方法与安全性[J].建筑结构, 2013, 43(23): 81-86.

ZHANG Wang-xi, YI Wei-jian. Checking calculation method and reliability of bearing capacity of RC members under torsion and bending[J]. Building Structure, 2013, 43(23): 81-86. (In Chinese)

[5] 廉晓飞, 王振东, 王仲秋. 钢筋混凝土矩形截面无腹筋梁剪扭工作性能的试验研究[J].哈尔滨建筑工程学院学报, 1985(1): 17-22.

LIAN Xiao-fei, WANG Zhen-dong, WANG Zhong-qiu. An experimental research of the behavior of rectangular reinforced concrete beams without web reinforcement under combined torsion, shear and bending[J]. Journal of Harbin University of Civil Engineering and Architecture, 1985(1): 17-22. (In Chinese)

[6] 廉晓飞, 王振东, 王仲秋. 钢筋混凝土矩形截面有腹筋梁剪扭工作性能的试验研究[J].哈尔滨建筑工程学院学报, 1985(1): 23-30.

LIAN Xiao-fei, WANG Zhen-dong, WANG Zhong-qiu. An experimental research of the behavior of rectangular reinforced concrete beams with web reinforcement under combined torsion, shear and bending[J]. Journal of Harbin University of Civil Engineering and Architecture, 1985(1): 23-30. (In Chinese)

[7] 钢筋混凝土结构抗扭专题组. 弯、剪、扭共同作用下钢筋砼构件的强度[J].建筑结构学报, 1985, 10(5): 2-11.

Research group on torsion of reinforced concrete structure. Strength of reinforced concrete members under combined action of bending, shear and torsion[J]. Journal of Building Structures, 1985, 10(5): 2-11. (In Chinese)

[8] 丁大钧. 学习《混凝土结构设计规范》(GBJ 10-89)的浅见[J]. 工业建筑, 1992(6): 2-7.

DING Da-jun. The suggestion of studying design code (GBJ 10-89) [J]. Industrial Construction, 1992(6): 2-7. (In Chinese)

[9] 康谷贻, 王士琴. 弯剪扭共同作用下钢筋混凝土构件的强度[J]. 天津大学学报, 1986(1): 11-23.

KANG Gu-yi, WANG Shi-qin. Ultimate strength of reinforced concrete members under the combined action of bending, shear and torsion[J]. Journal of Tianjin University, 1986(1): 11-23. (In Chinese)

[10]黄靓, 陈胜云, 李建伟，等. 对钢筋混凝土剪扭构件承载力计算公式的修正[J].土木工程学报, 2010, 43(4): 46-52.

HUANG Liang, CHEN Shen-yun, LI Jian-wei,etal. Modification of the bearing capacity formula of reinforced concrete members under shear and torsion[J]. China Civil Engineering Journal, 2010, 43(4): 46-52. (In Chinese)

[11]黄靓, 鲁懿虬, 徐紫鹏. 钢筋混凝土剪扭构件承载力可靠度分析[J]. 工程力学, 2012, 29 (4): 185-191.

HUANG Liang, LU Yi-qiu, XU Zi-peng. Reliability analysis of reinforced concrete members under the combined action of shear and torsion[J]. Engineering Mechanics, 2012, 29(4): 185-191. (In Chinese)

[12]GB 50010-2010 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010:64-73.

GB 50010-2010 Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2010:64-73. (In Chinese)

[13]叶列平, 冯鹏, 林旭川, 等. 配置FRP的结构构件的安全储备指标及分析[J].土木工程学报, 2009, 42(9): 21-31.

YE Lie-ping, FENG Peng, LIN Xu-chuan,et，al. Analysis of safety margin indices for structural members with FRP[J]. China Civil Engineering Journal, 2009, 42(9): 21-31. (In Chinese)

Study on the Calculation Formula of Reinforced Concrete Members under Shear and Torsion

ZHANG Wang-xi†,HAN Jiang

(College of Civil Engineering, Hunan Univ, Changsha，Hunan 410082,China)

It is pointed out that the Tri-linear Model in Concrete Structure Design Code GB 50010-2010 for calculating the bearing capacity of reinforced concrete members under the combined action of shear and torsion enlarges the 1/4 Circular Arc Model and leads to an unsafe design. The formula proposed by Ding Dajun using the 1/4 Circular Arc Model understates the bearing capacity of concrete in choosing the reduction factor of concrete shear capacity. The formula proposed by Huang Liang using the Linear Model makes the design conservative. On the basis of the 1/4 Circular Arc Model, two modified formulas were provided. Practical examples show that Formula 1 and Formula 2 are more secure than the Code formula. Numerical examples show that Formula 1 and Formula 2 not only totally conform to the 1/4 Circular Arc Model , but also approximately conform to the Linear proposed by Huang Liang, and their calculation results are quite similar.

reinforced concrete; shear-torsion member; calculation of bearing capacity; modified formula

1674-2974(2015)07-0048-08

2015-03-11

国家自然科学基金资助项目(51078133,51208190)，National Natural Science Foundation of China(51078133,51208190)

张望喜(1971-)，男，湖北黄冈人，湖南大学副教授，博士

†通讯联系人，E-mail: wxizhang2000@163.com

TU470.3

A